车床自动送料机构的棒料振动变形分析

崔鑫伟，李金良，于 冲

(燕山大学 机械工程学院，河北 秦皇岛 066004)

0 前言

使用自动送料机可以显著地提高自动化车床的加工效率。但在实际运行过程中，由于所输送棒料的形状特点及其受力特点，在主轴高速回转下，棒料容易发生挠曲变形[1-2]。该变形会导致棒料与送料机的内壁发生碰撞，产生振动，损坏送料机的内部结构[3]。另外振动会使棒料加工过程中与刀具产生碰撞，轻则产生振纹，影响加工表面的光洁度、粗糙度，甚至尺寸精度；重则损坏刀具，对主轴产生不利的影响[4-5]。

自动送料机中棒料的振动强弱直接影响工件的加工精度，因此需对送料系统的相关参数进行研究。棒料的振动主要在其回转过程中的挠曲变形引起，而影响这种变形的主要原因与车床的主轴转速、棒料的直径、送料器所用液压油的粘度等有关。因此本文应用有限元软件ANSYS Workbench模拟自动送料机中棒料在不同工况参数下的回转，得到棒料在工作过程中的模态、谐响应特性，并研究不同的主轴转速、液压油牌号以及初始间隙对棒料变形的影响，以期减小棒料的振动变形，从而为实践应用提供一定的理论参考。

1 送料机的结构与工作原理分析

自动送料机的核心部件为棒料导管，结构如图1所示。位于送料导管中的棒料，其一端与推料杆接触，并由液压油通过活塞、推料杆推动，实现自动上料功能；而另一端被车床主轴夹持固定。车床主轴未转动时，棒料静置于送料导管底壁；主轴转动以后，由流体动压效应[6]可知，棒料与导管之间会产生润滑油膜，减小两者之间的摩擦。并且该润滑油膜有支撑作用，可抑制棒料的振动变形。

图1 棒料导管结构图

2 数值分析模型建立

2.1 结构场分析模型建立

简化后的送料系统模型如图2所示，由于该模型为轴对称的形式，因此采用扫描的方法来划分网格，网格的类型为六面体。

图2 简化后的送料系统几何模型

根据送料系统的受力特点，设置边界条件：对位于送料导管内的棒料端面采用圆柱约束；对于棒料被主轴加持的那一部分，主要是限制其沿X、Y、Z三个方向的位移以及绕X、Y方向的旋转，因此可同时施加圆柱约束与Z方向位移约束。求解器参数设置：时间步长为0.05 s，步数为100步，其余参数可保持默认。所研究的自动送料机的送料导管以及棒料的材料均为45钢，设置的材料属性见表1。

表1 材料属性表

2.2 流体场分析模型建立

自动送料机采用HL型液压油，该型号的液压油可选用的牌号为22～100。在送料机运行过程中，液压油在不断循环，存在良好的散热条件，因此仿真分析中可以忽略由于液压油的内摩擦而导致油温升高、粘度下降的问题。另外，送料导管与棒料之间的间隙并不大，所以最终在CFX中采用层流模型，并关闭热能方程。

流体边界条件设置：进口油压的压力大小为0.3 MPa，出口油压的压力大小为0 MPa；将流体与送料导管的接触面以及与棒料的接触面设置为Wall[7]。但在自动送料机工作时，送料导管静止不动，棒料在高速回转，因此可设置与棒料的接触面为流固耦合面，并设置网格的运动方式为ANSYS Mutli-Field，流体场与结构场的载荷传递方式为Total Mesh Displace-ment[8]。其余参数保持默认，并在流体场求解之前将各参数初始化为0。

2.3 耦合设置

棒料在高速回转过程中会发生弯曲变形，并与送料导管内壁发生碰撞，产生振动，损伤自动送料机内部的其他零件。而棒料回转过程中的流体动压效应对这种情况有抑制作用。因此棒料的振动变形程度与流体动压效应的强弱都与棒料的转速、液压油的粘度以及棒料与送料导管的间隙有关。为研究棒料的振动变形问题，需将棒料的瞬态动力学模型与送料系统的流体力学模型耦合在一起[9]，送料系统的分析流程如图3所示。

图3 双向流固耦合分析流程图

使用Geometry模块，将结构场模型与流体场模型同时建立在一个几何文件中。使用Mesh模块对模型依次完成结构场与流体场的网格划分。进入Transient Structure模块，对结构场模型完成瞬态动力学分析所需的边界条件、载荷以及耦合面的设置。进入CFX模块，完成对流体场模型的相应设置。

先进行结构场的瞬态动力学分析，并将当前时间步的计算结果通过耦合面传递至流体场中。该计算结果将作为位移载荷施加在耦合面上，并成为即将要执行的时间步的边界条件。在流体场分析完成后，耦合面上的流体压力将作为压力载荷施加在结构场的分析中。如此循环往复地在两个物理场之间传递计算结果，可完成双向流固耦合分析。

3 模态分析

研究棒料在回转过程中变形问题，要在进行瞬态动力学分析之前先完成对棒料系统的模态分析，求得棒料系统的固有频率及对应的模态振型，对后续送料系统中棒料的振动变形分析提供一些指导依据[10]。在多自由度线性系统中，无阻尼自由振动方程可表示为

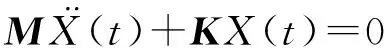
(1)

式中，M为系统质量矩阵；K为系统刚度矩阵；X(t)为系统位移方程。

要得到棒料系统的固有频率和振型，即求解式(1)的广义特征值和特征向量，而利用Modal模块，可方便地计算出来。模型的前6阶固有频率如图4所示，对比发现第1阶与第2阶之间的固有频率值虽说有上升的趋势，但两者之间变化不大，仅为0.004%。而这种情况在第3阶与第4阶、第5阶与第6阶之间的固有频率值上也一直存在，并且随着阶数m的上升，这种差值也在不断变大。

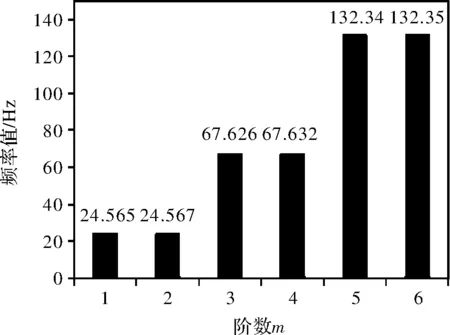
图4 棒料系统的前6阶固有频率

类似的特点也体现在棒料系统的模态振型中，如图5所示。比较发现由于棒料系统本身的结构以及受力状态均为轴对称的形式，在第1和第2阶、第3和第4阶、第5和第6阶模态振型彼此正交。

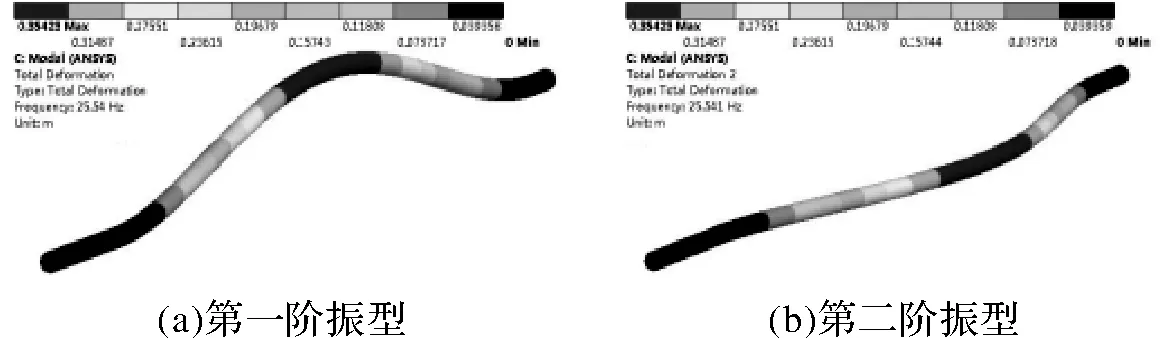
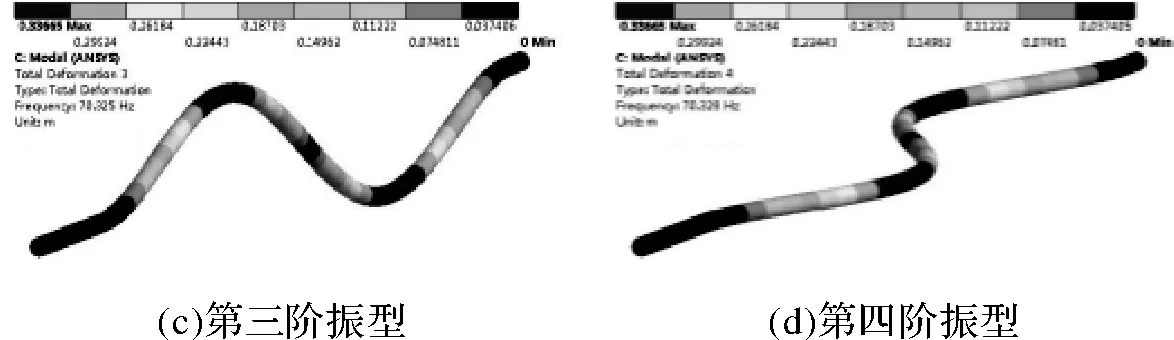
图5 棒料系统的前6阶模态振型

4 谐响应分析

车床启动以后，装夹在主轴上的棒料会受到来自车床主轴的激振力的作用。在该力的影响下，棒料会作受迫振动，并对自动送料机，车床主轴系统以及刀具等产生损伤。特别是在棒料发生共振的情况下，这种损伤会变得非常严重。因此在对送料系统进行双向流固耦合分析之前需进行谐响应分析[11]。主轴系统对棒料施加的激振力可表示为

F=(F1+iF2)eiωt

(2)

式中，ω为激振力的频率。

由此，本文谐响应分析的动力学基本方程为

-ω2M+iωC+K(X1+iX2)=F1+iF2

(3)

设置主轴系统对棒料施加的激振力为2 300 N，此时棒料系统的幅频响应曲线如图6所示。当频率值为20 Hz附近时，棒料系统的振幅值达到最大，约为18 mm。说明此时系统发生共振，由图4可知，该频率值与第1、2阶的固有频率相近。另外随着频率值的提高，棒料系统的振动幅值在频率值大于37.5 Hz以后出现平缓下降，并在频率值为135 Hz的附近达到稳定。该频率值与第5、6阶的固有频率值相近，此时棒料系统的振动幅值约为1 mm。

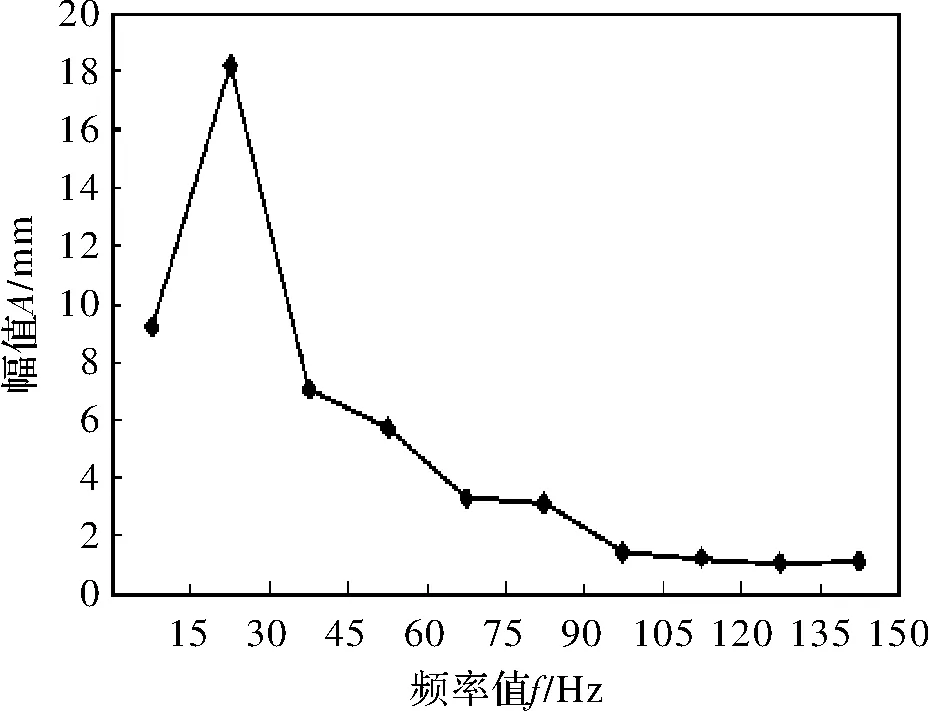
图6 幅频响应曲线

5 流固耦合计算结果分析

5.1 转速对棒料变形的影响

棒料的最大变形由节点的最大位移表示，并以该值的大小来表征棒料的变形程度。设置送料导管的内径D为44mm，液压油的牌号为46，依据所需的切削速度，分析转速对棒料变形的影响，并依次取棒料的直径d为34 mm、36 mm、38 mm、40 mm、42 mm，以作更为充分的对比，如图7 所示。

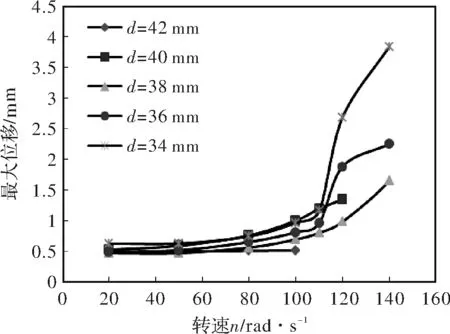
图7 转速变化对棒料变形的影响

整体而言，棒料节点的最大位移均随着转速的增大而增大。当转速n较低，约为80 rad/s时，棒料的最大位移随转速的增加上升较为平缓。说明在这段转速范围内，流体动压润滑膜对棒料变形的抑制作用较为明显。特别在转速n小于50 rad/s时，棒料的最大位移几乎不随转速发生变化。而在转速n大于80 rad/s时，不同直径棒料的最大位移均出现了大幅上升，说明此时原来的流体动压润滑膜已无法支撑变形的棒料，油膜受棒料的压迫而变薄。由图7中数据可知，这个阶段的棒料最大位移小于棒料与送料导内壁的间隙，即此时液压油润滑膜依旧存在。另外在转速相同的情况下，直径越小的棒料的最大位移也就越大，而当棒料直径d为40 mm时却出现了反常。特别是在转速n为80 rad/s、100 rad/s、110 rad/s时，其最大位移几乎与直径d为36 mm的棒料一致。分析可知，这可能是由于此时棒料系统发生了共振。

5.2 液压油变化对棒料变形的影响

棒料在送料系统中的变形与流体动压效应的强弱有关，而液压油的粘度又是流体动压效应的影响因素之一。对于HL型液压油的五种牌号(依次为22、32、46、68、100)而言，牌号越大，油的粘度也越大。因此取送料导管的内径D为44 mm，车床主轴的转速n为100 rad/s，对直径d为40 mm、34 mm的两种棒料进行分析，仿真结果如图8所示。

图8 液压油牌号对棒料变形的影响

随着液压油牌号的增加，即油的粘度增加，两种直径棒料的最大位移均出现了不同程度的下降。对于直径较大的棒料，其最大位移随液压油牌号的变化关系近似线性，而且比较平缓。说明在棒料直径较大时，使用不同牌号的液压油并不会对棒料变形产生太大的影响。

但在棒料直径较小时则不同，在液压油牌号依次为22、32、46的工况下，棒料的最大位移出现了明显下降。这意味着在棒料直径较小时，液压油粘度对棒料变形的影响相当明显。而在液压油牌号分别为68、100时，棒料的最大位移几乎没有发生太大的下降，即棒料变形不再受到液压油粘度变化的影响。

在相同的自动送料机运行条件下，液压油粘度越大，油温上升就越快，这会导致油的粘度下降以及其他不利的影响。因此综合经济因素考虑，使用46号或者68号的液压油均是不错的选择。

5.3 初始间隙对棒料变形的影响

棒料的直径与送料导管内径的差值为初始间隙，该间隙的大小会影响流体动压效应的强弱，进而改变棒料的振动变形程度。仿真实验结果如图9所示，初始间隙的取值为1 mm、2 mm、3 mm、4 mm、5 mm，在送料导管内径D为44 mm的情况下，对应的棒料直径d依次为34 mm、36 mm、38 mm、40、42 mm。

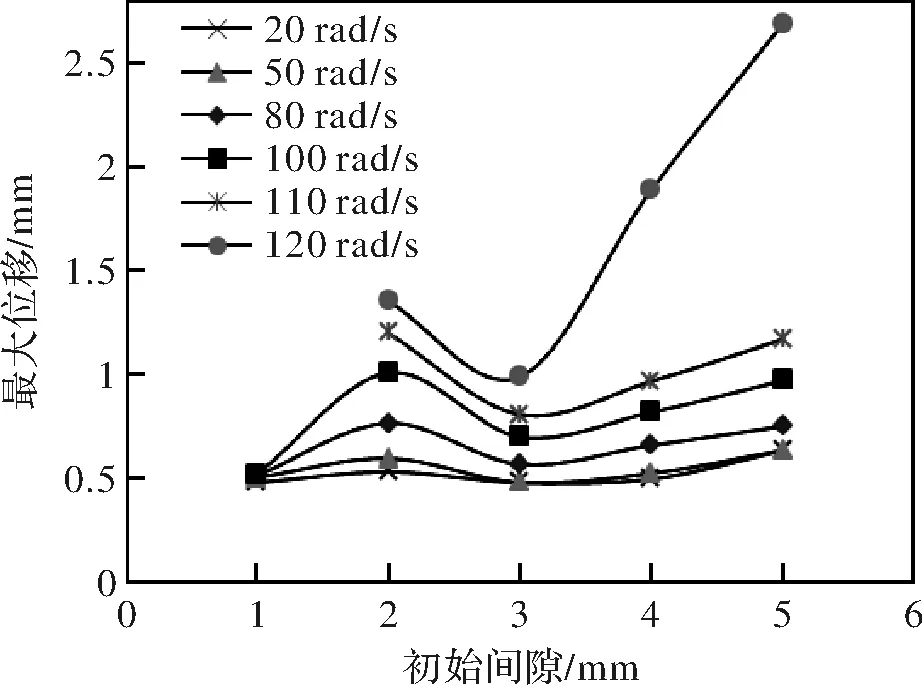
图9 初始间隙对棒料变形的影响

当初始间隙为1 mm，即棒料直径d为42 mm时，在不同的转速下，棒料的最大位移几乎不变。比较最大位移值与初始间隙值，可以发现此时的流体动压润滑膜依旧存在。这说明在间隙较小时，油膜的支撑能力良好，设备运行稳定。而在间隙值大于3 mm之后，棒料的最大位移随间隙值的增大而增大，并且棒料的转速越高，这种增大的幅度也就越大。这意味着在使用自动送料机输送较细的棒料时，不应将车床的转速设置过高。并且为保证加工质量，在编排加工工艺时，应尽量控制切削速度的大小。

特别的，在初始间隙为2 mm时，除转速n为110 rad/s、120 rad/s之外，其余所有转速下的棒料变形，都在该条件下出现了极大值，这种情况与图7中一致。而在初始间隙为3 mm的情况下，所有转速工况均出现了极小值。

结合图7与图9的数据进行分析，可以得到在使用牌号为46的HL型液压油时，棒料在不同直径、不同转速下的最大位移正交表如表2所示，利用表2的数据，可在使用自动送料机之前，结合棒料的直径以及主轴转速，初步判断棒料的振动变形情况，在提高了上料速度的同时，保障车床的加工质量。

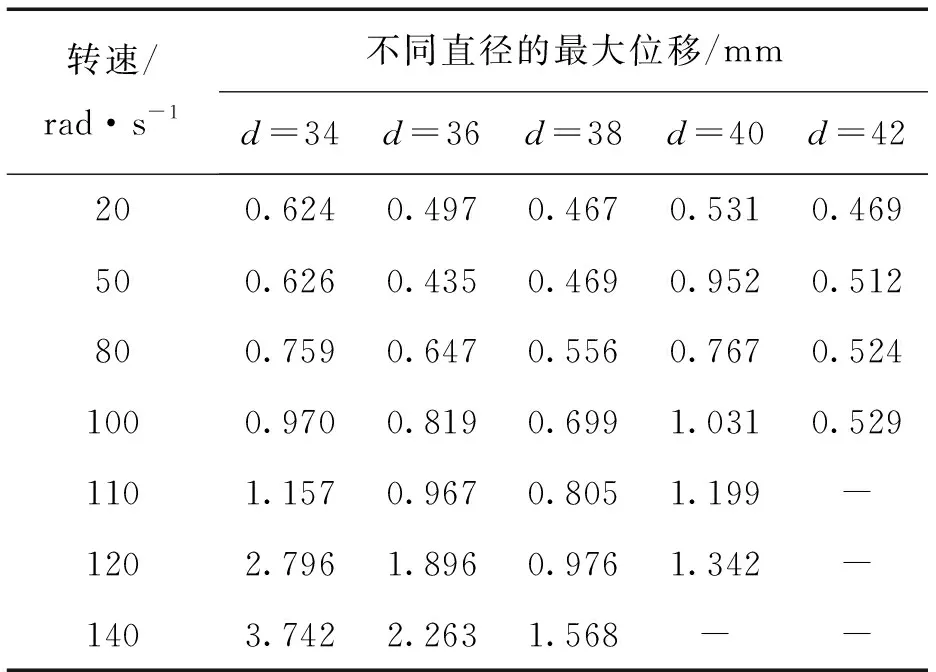
表2 棒料在不同直径、不同转速下的最大位移

6 结论

对送料机送料系统建立数值模型，研究棒料系统的模态振型，谐响应特性以及车床转速、液压油牌号、初始间隙对棒料变形的影响，为生产实践提供理论指导。研究表明：

(1)当车床主轴转速较小时，棒料变形程度随主轴转速的增加而缓慢增大，在超过一定转速以后，棒料的变形程度会突然增大。

(2)相比于直径较大的棒料，直径较小的棒料其变形程度更易受到液压油粘度的影响，但整体上呈现随液压油粘度增大，变形程度减小的趋势。

(3)当棒料与送料导管的间隙大于3 mm时，棒料变形随间隙的增大逐渐加大；在小于3 mm时，与间隙变化的关系曲线近似抛物线，并在间隙值为2 mm附近出现极大值，3 mm附近出现极小值。间隙过大或过小都会导致棒料变形加大。