声屏障顶部开口间距对列车风效应的影响
2022-03-29吉晓宇邹云峰何旭辉黄永明蒋硕
吉晓宇,邹云峰,何旭辉,黄永明,蒋硕
(1.中南大学土木工程学院,湖南长沙,410075;2.高速铁路建造技术国家工程实验室,湖南长沙,410075)
近年来,高速铁路的迅速发展给人们的出行带来了极大便利,但列车高速运行产生的噪声问题也引起了人们的广泛关注[1]。在线路两侧布置声屏障能有效控制高速铁路噪声的传播,被认为是一种降低高速铁路噪声的有效措施,目前已得到广泛应用[2]。然而,高速列车行驶时,列车周围的空气随列车一起运动形成强烈的列车风,会在毗邻的声屏障表面产生极大的瞬态风荷载,使声屏障在极短时间内受到交变的压力波作用[3],可能导致结构发生强度或疲劳破坏,进而危及行车安全。
事实上,2003年便发现德国科隆至法兰克福线路采用的声屏障因列车风致荷载作用而出现损伤,为此,国内外研究者通过动模型试验、风洞试验、现场实测和数值模拟方法对列车行驶时产生的脉动风压问题进行了深入研究,如:BAKER[4]通过动模型试验研究了列车明线行驶时的流场及轨边结构的列车风致荷载;BELL等[5-6]通过风洞试验和动模型试验研究了高速列车周围的流场和尾流;GILBERT等[7]利用动模型试验研究了列车明线运行和通过不同类型轨边结构时的风荷载和瞬时风速;XIONG等[8]对京沪高铁两侧的声屏障进行了实车测试,研究了列车速度、运行线路、测点位置、编组长度和环境风速对动车组在声屏障上引起的风荷载的影响;邹云峰等[9]对CRH380型动车组作用下桥上风屏障风荷载进行了实测,并对荷载多分率进行了分析;SOPER 等[10]进行了一系列现场实验评估声屏障上的风荷载,发现声屏障上的风荷载与车型有关,建议载荷计算应考虑铁路上行驶的交通类型;LÜ 等[11]通过现场测试研究了列车速度和列车与声屏障之间的距离对声屏障上风荷载的影响,发现随着列车速度提高,作用于声屏障上的风荷载不断增加,随着火车与声屏障之间距离减小,声屏障上的风荷载对速度更加敏感;艾辉林等[12]利用大涡模拟方法研究了速度为350 km/h 的列车通过时道路及桥梁两侧布置的不同高度声屏障上列车风致荷载分布特性,发现极值风压随声屏障高度增加而减小;龙丽平等[13]采用CFX 软件建立计算模型,对高速列车驶过直立式声屏障时引起的风荷载变化规律进行了研究,分析了列车运行速度对风荷载的影响;戚振宕等[14]利用k-ε两方程紊流模型研究了直立型、倒L 型、内倾45°型这3种声屏障上的气动力与车速的关系,对比了单车与会车过程中的声屏障气动特性;王宏朝等[15]利用流体力学软件Fluent研究了在列车风与自然风联合作用下的高速铁路声屏障及风向角和风速对声屏障所受风压的影响;罗云柯[16]以杭长线金华区半封闭声屏障为工程背景,建立了半封闭声屏障数值计算模型,对声屏障内风荷载分布规律及列车风致振动进行了研究;施洲等[17]结合数值模拟技术与现场实测结果,提出速度为380~400 km/h的高速列车风荷载的最大风压建议值。
由以上分析可看出,已有研究大多重点针对直立式声屏障的列车致风荷载,在一些对噪声控制要求非常严格的地区尝试建设全封闭型声屏障,以尽可能提高降噪效果,但全封闭的结构型式导致声屏障的列车风效应愈加突出,需要对声屏障顶部开口间距进行研究,以尽可能减小声屏障列车风效应又不显著影响降噪效果。为此,本文作者以顶部不同开口间距的声屏障为研究对象,综合考虑声屏障风荷载和列车表面风压,采用数值模拟技术对速度为350 km/h 列车通过顶部不同开口间距声屏障时的列车风效应进行系统研究,以期为高速铁路全封闭和半封闭声屏障结构设计提供参考。
1 数值模拟
1.1 数值计算模型
以高速铁路常用的CRH2 高速列车为研究对象,已有研究表明列车长度对列车风效应影响有限。列车采用3列编组,由头车、中车、尾车组成,车体宽为3.38 m,高为3.70 m,总长为76.40 m。本文采用的CRH2 模型考虑了风挡、转向架、裙板等,根据文献[18]的建议,略去受电弓,列车时速为350 km/h,如图1所示。
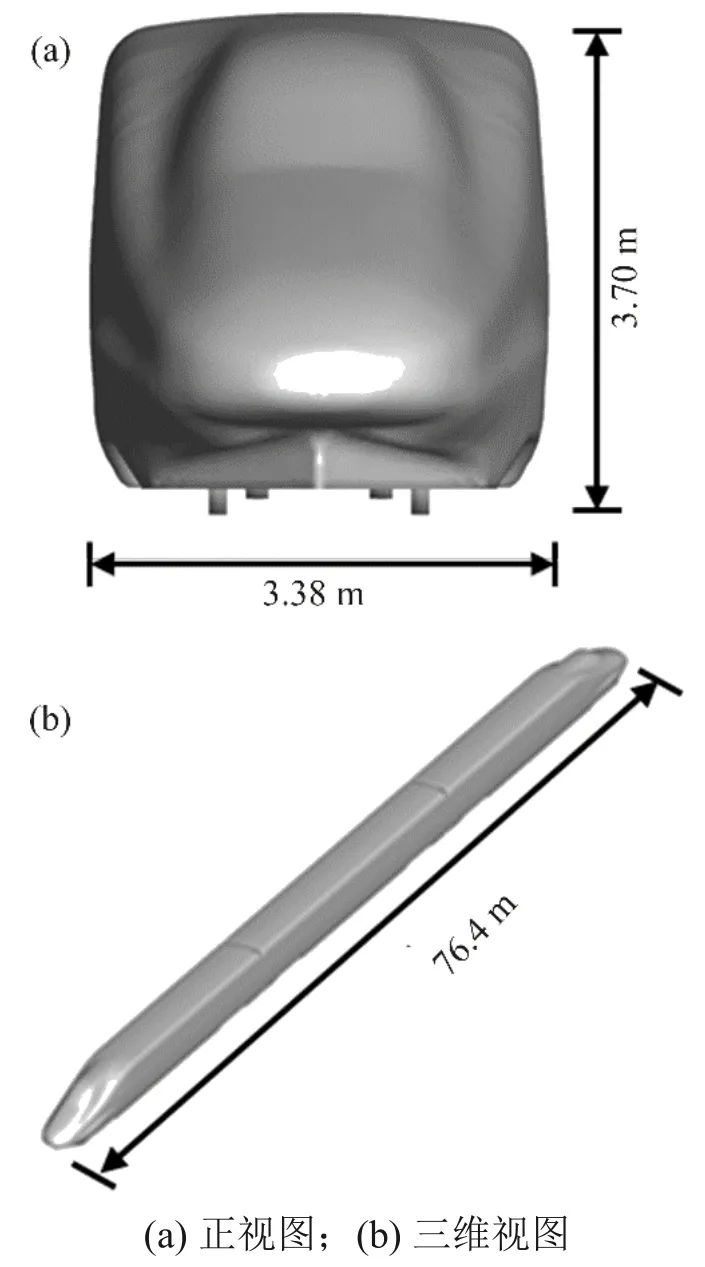
图1 高速列车计算模型Fig.1 High-speed train calculation models
声屏障数值模型以我国某在建高铁线路声屏障为原型,根据结构设计初步方案,声屏障内线路为双线轨道,宽×高为12.0 m×8.1 m,总长为410.0 m,在顶部正中间对称开口。为研究高速列车通过时顶部开口间距对列车风效应的影响,考虑顶部开口间距L为0 m(全封闭),0.1,0.5,1.0,2.0,4.0,6.0和8.0 m共8种情况,如图2所示。
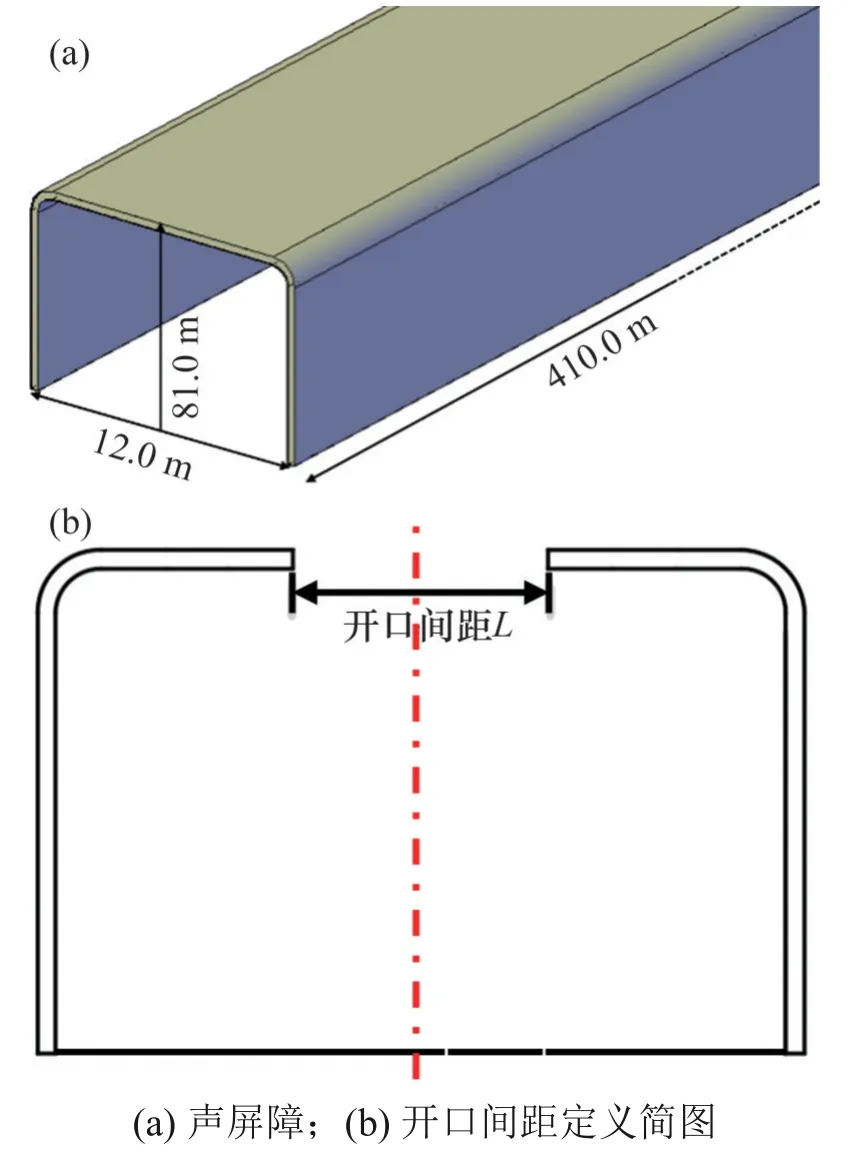
图2 声屏障计算模型Fig.2 Calculation models of sound barrier
1.2 计算区域及边界条件
计算模型分为2个区域,其中,一个是包含声屏障的静止区域,另一个是包含高速列车的移动区域,通过设置交界面实现静止区域与移动区域之间的数据交换。根据文献[19]的建议,静止区域长×宽×高为585 m×120 m×60 m,声屏障置于静止区域中部,计算长度为410 m。为避免列车对声屏障入口处的影响,列车初始位置位于距离声屏障入口50 m处。计算域入口和出口定义为压力出口,地面、声屏障、车体均定义为无滑移固体壁面,计算域两侧、顶部均定义为对称边界。计算区域及边界条件见图3。
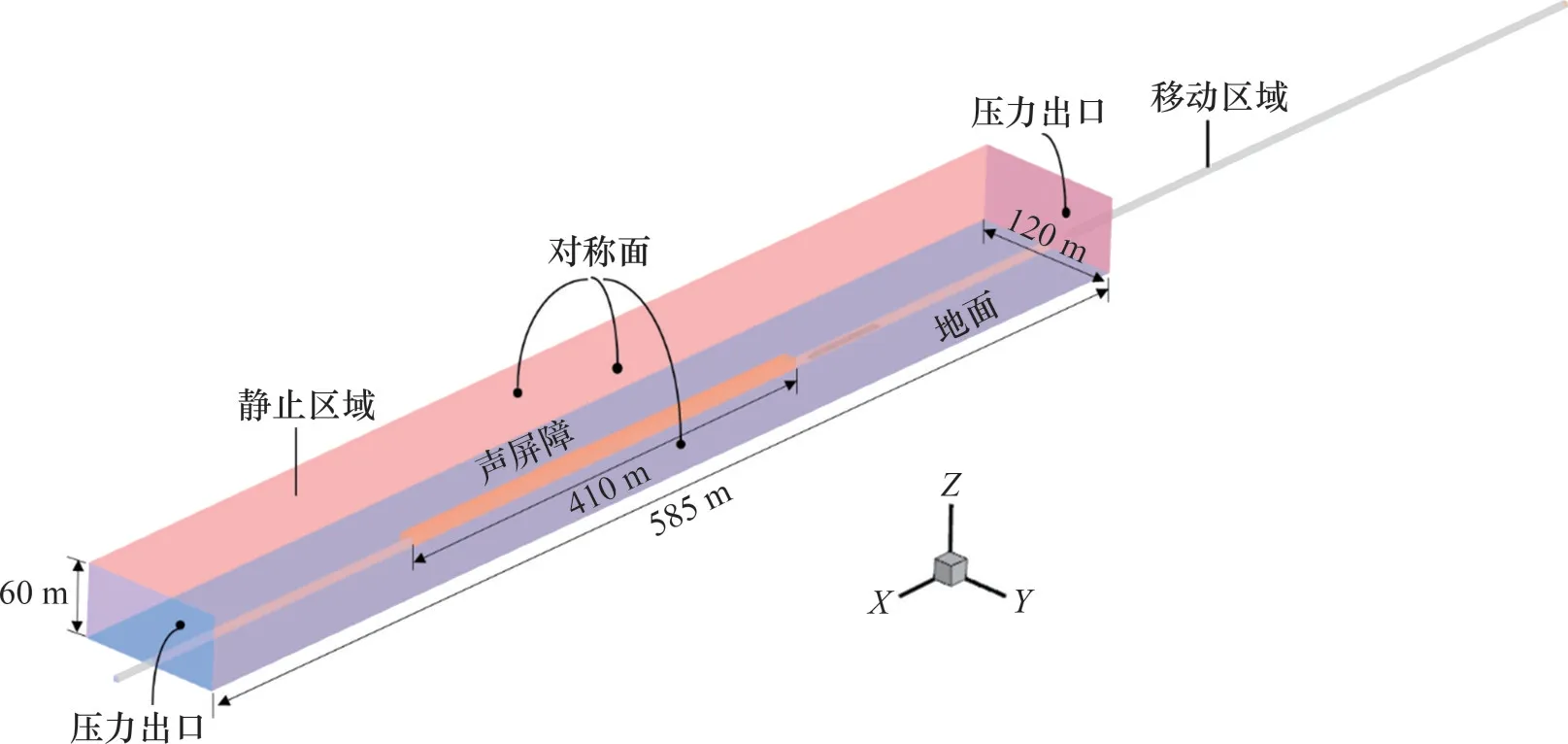
图3 计算区域及边界条件Fig.3 Calculation domain and boundary conditions
1.3 网格划分
采用gambit 软件对计算模型网格进行划分。为了精确模拟列车车体周围的流场,对车体周围网格进行加密,对地面、声屏障壁面等流动变化剧烈的区域合理加密网格,对远离声屏障和列车的区域,网格逐渐稀疏,从而减少网格总量,提高计算效率。计算模型采用六面体非结构化网格和棱柱层网格,如图4 所示。通过对比细网格(2 400 万个)和粗网格(1 600 万个)的计算结果进行网格无关性检验。利用粗网格和细网格对列车以350 km/h 通过顶部开口8 m 声屏障的过程进行计算。图5所示为使用2种网格计算得到的距声屏障入口100 m处P10点的压力时程曲线,这2种网格计算得到的压力峰值(即压力正峰值与压力负峰值之差)分别为402.2 Pa 和393.6 Pa,相对差为2.18%,说明采用网格量为1 600万的网格既能满足计算精度的要求,又能提高计算效率。
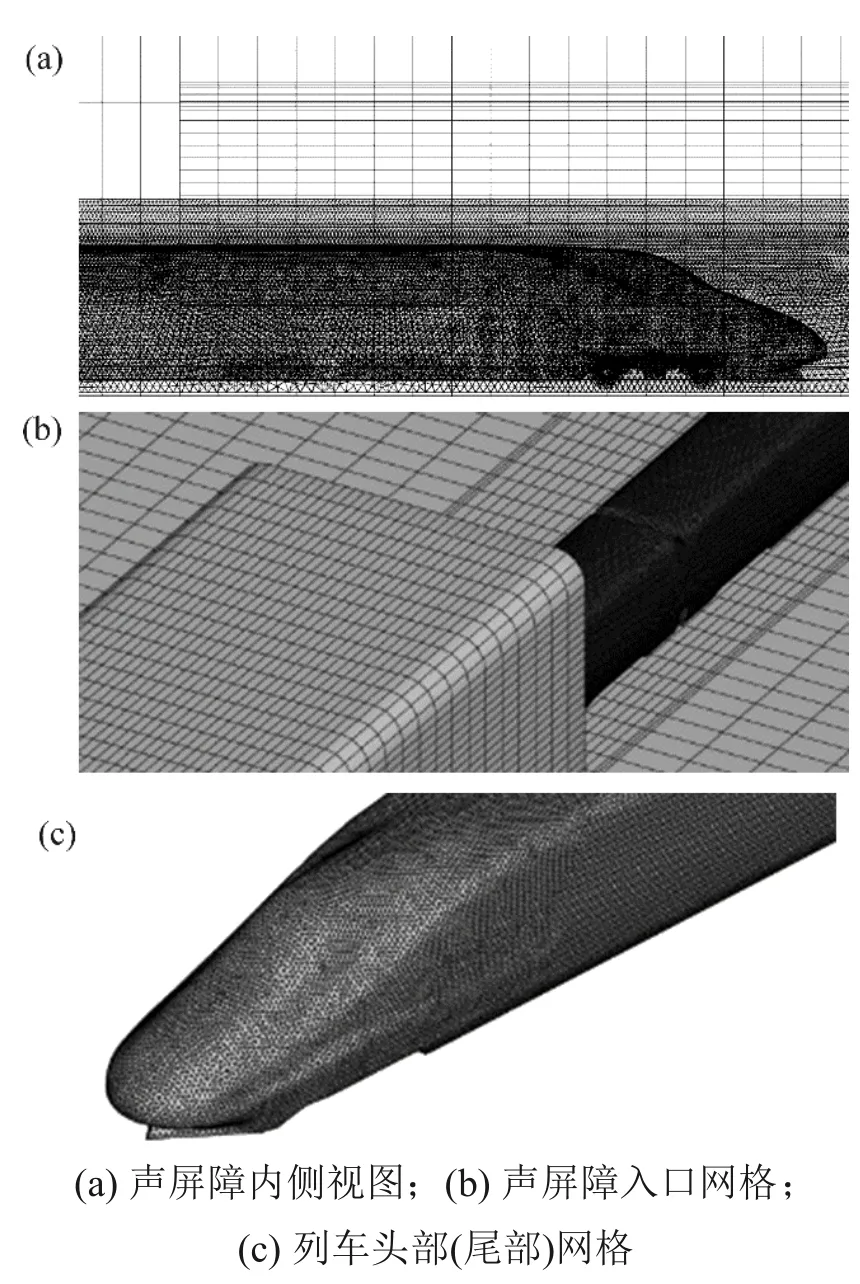
图4 网格划分Fig.4 Grid generation
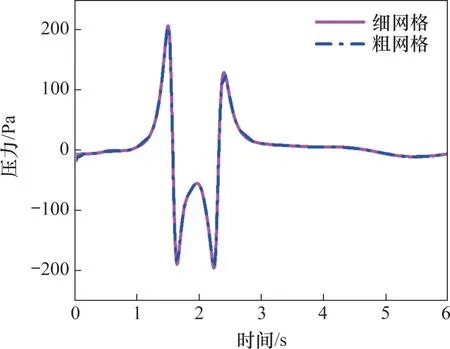
图5 不同网格量计算得到的压力时程曲线Fig.5 Relationship between pressure and time in different mesh resolutions
1.4 计算方法
声屏障内空气受壁面的限制无法自由流动,高当速列车通过声屏障时,空气会受到声屏障壁面和车体的强烈挤压,流场处于湍流状态,需考虑空气的压缩性。因此,数值计算采用非定常、黏性、可压缩N-S 方程,湍流模型为标准两方程k-ε模型[20]。标准k-ε模型的湍流动能k和耗散率ε方程如下:
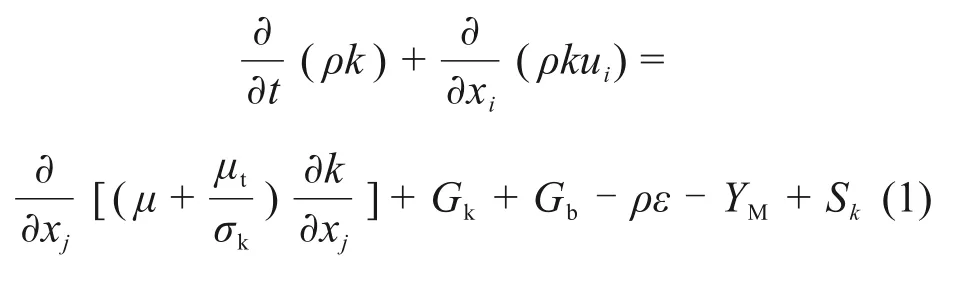
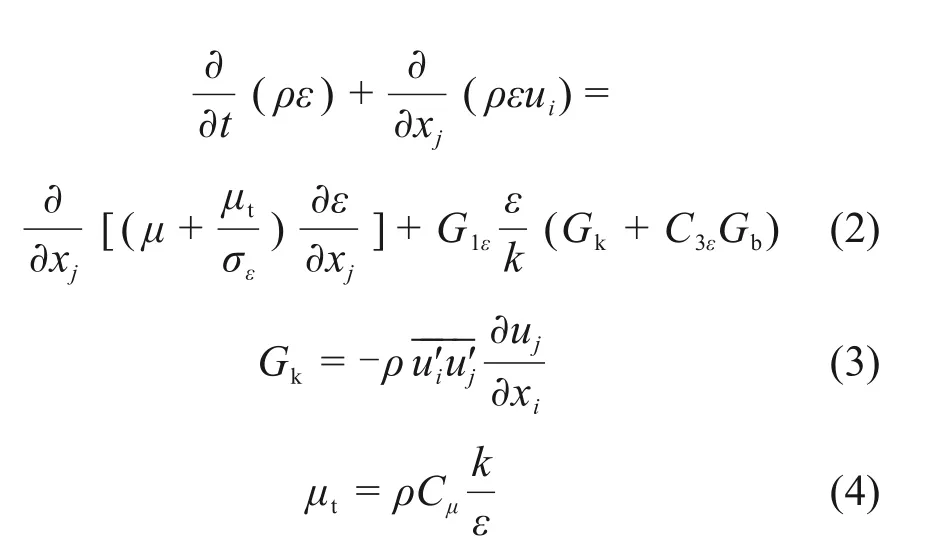
式中:k为湍流动能;ε为湍流耗散率;ρ为空气密度;t为时间;xi和xj为笛卡尔坐标(i=1,2,3;j=1,2,3);μ为空气压力黏度;ui和uj分别为列车周围流场在xi和xj方向上的速度分量;Gk为层流速度梯度而产生的湍流动能;Gb为由于浮力产生的湍流动能;Ym为可压缩湍流中脉动扩张的贡献量;μt为湍流黏性系数。其中,模型常数Cμ=0.09,C1ε=1.44,C2ε=1.92,C3ε为与浮力有关的常量,可忽略;湍流动能k与耗散率ε的湍流普朗特常数分别为σk=1.0,σε=1.3。
利用大型通用流体计算软件Fluent 进行计算,采用SIMPLEC 算法,根据文献[21]建议,计算时间步长取0.008 57 s,为保证每步计算达到收敛,内迭代次数为30 次。所有工况的计算过程均为列车从距离声屏障入口50 m 处出发,至列车车尾离开声屏障出口50 m处为止。
1.5 测点布置
由于声屏障内单线行车情况更普遍,数值计算暂只考虑单线行车情况。在声屏障纵向布置9个截面,每个截面上共布置15 个测点(顶部开口后,对应开口位置的测点一起去掉)。截面及各截面测点布置如图6所示。
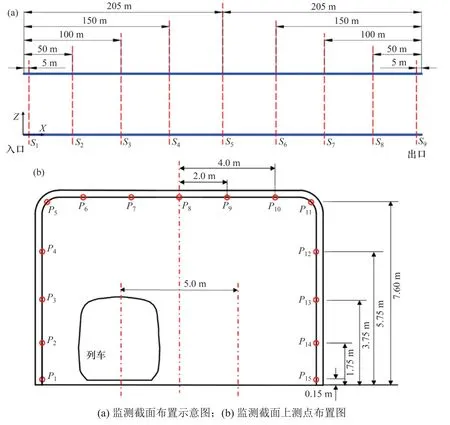
图6 声屏障壁面测点布置Fig.6 Positions of measuring points on a monitoring cross-section
2 方法验证
为验证数值模拟方法的准确性,以顶部开口8 m 声屏障为例,对高速列车动模型进行试验验证。试验在中南大学的列车气动性能动模型试验系统进行。该试验系统由双轨组成,分为发射段、试验段和减速段,总长163 m,列车模型的最高行驶速度可达400 km/h。试验使用1.0∶16.8 的动车组模型,由头车、中车和尾车组成,宽度和高度分别为0.201 m 和0.220 m,总长4.548 m;声屏障模型长为24.400 m。声屏障和列车模型的实际布置情况以及测量系统如图7所示,在声屏障壁面布置压力传感器用来测量壁面压力变化。试验前,对每个传感器重新进行校准和标定,完全满足试验精度要求,试验车速为350 km/h。

图7 动模型试验平台Fig.7 Dynamic model test rig
依照1.3中方法对试验中采用的模型进行网格划分,采用与试验相同的边界条件与车速。由动模型试验和数值模拟这2种方法所测得的单列车以350 km/h 速度通过声屏障时,距声屏障入口55.00 m,近车侧离地面5.25 m处(对应于声屏障实际尺寸)测点的压力时程曲线如图8所示。从图8可见:数值模拟计算得到的测点压力与动模型试验测得的压力变化趋势基本一致,证明了本文采用的数值模拟计算方法的可行性。
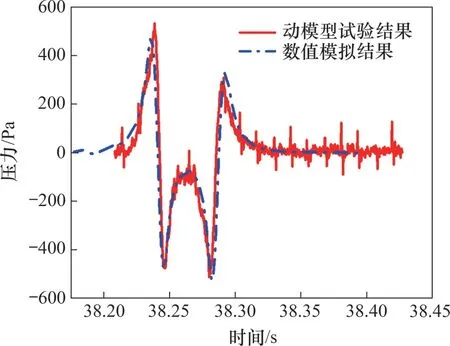
图8 数值模拟计算与动模型压力试验结果对比Fig.8 Comparison between numerical calculation pressures and dynamic model test pressures
3 计算结果与讨论
3.1 开口间距对声屏障线路纵向压力分布的影响
为研究350 km/h 高速列车通过顶部不同开口间距声屏障时声屏障纵向压力分布规律,绘制声屏障顶部不同开口间距下压力峰值随测压截面纵向位置的变化曲线,如图9 所示。从图9 可以看出:当列车通过全封闭声屏障时,声屏障中间部分的压力峰值高于靠近入口/出口处的压力峰值,最大压力峰值为5.945 kPa,出现在S5 截面;声屏障顶部开口0.1 m后,声屏障壁面各处压力峰峰值均有所下降,中间截面压力峰值下降幅度最大,为45.6%;随着声屏障顶部开口距离增大,各截面处的压力峰值逐渐降低;当开口间距为2~8 m 时,各截面处的压力峰值相差较小。
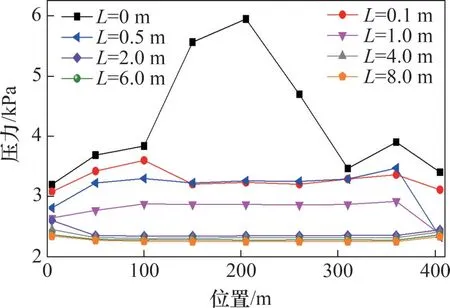
图9 压力峰峰值与截面测点纵向位置的关系Fig.9 Relationship between peak-to-peak values of pressure and longitudinal position of measured points on cross section
3.2 开口间距对声屏障横截面压力分布的影响
为了研究声屏障顶部开口间距对横截面压力分布的影响,以不同开口间距声屏障S5 截面为研究对象,所得S5 截面处左右两侧测点的压力时程如图10 所示(其中,N和T分别表示车头和车尾经过S5截面的时间)。从图10可以看出:列车经过全封闭声屏障时,压力不断变化,表现出一定周期性;当列车距离S5 截面较远时,各测点的压力变化基本相等;当列车经过S5 截面时,距离列车较近的测点压力变化量大于距离列车较远测点压力变化量,这与文献[19]中报道的基本一致。
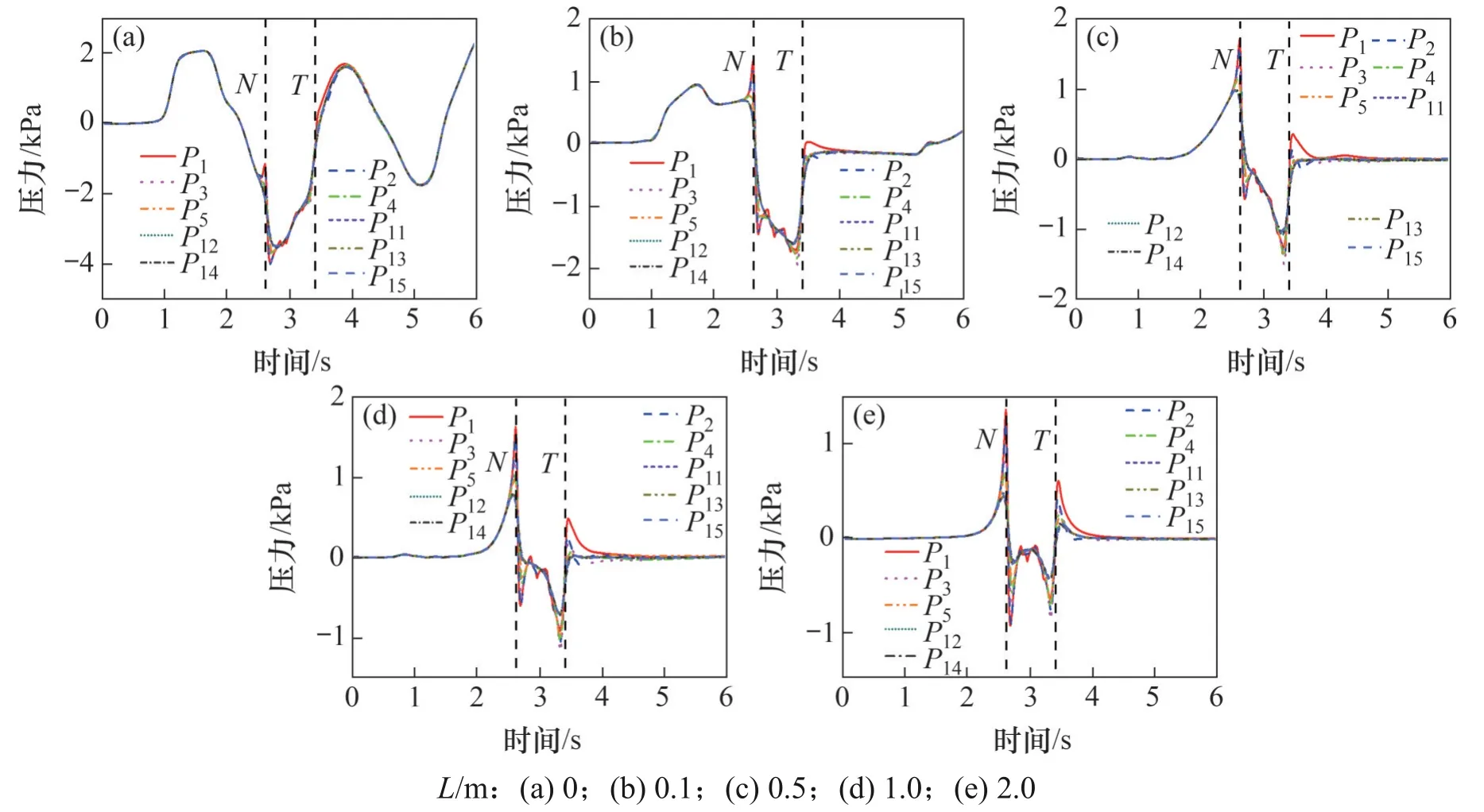
图10 顶部不同开口间距L下声屏障S5截面压力时程曲线Fig.10 Pressure time history curves on section S5 of sound barrier at different opening spacings
S5 截面测点的压力时程与压力波传播示意图如图11 所示,其中,红色实线和绿色实线分别表示车头和车尾的轨迹,紫色实线和蓝色虚线分别表示压缩波和膨胀波的传播轨迹。从图11 可以看出:车头驶入声屏障后产生压缩波,t1时传至S5截面,测点压力上升,车尾驶入声屏障时产生膨胀波;t2时传至S5截面,测点压力下降;压缩波传播到声屏障出口后,反射回来的膨胀波在t3时传至S5截面,测点压力持续下降;膨胀波传播到声屏障出口后,反射回来的压缩波在t4时传至S5 截面,测点压力上升;之后,多个压缩波、膨胀波传至S5 截面,测点压力随之上升、下降(t5,t6和t7时),此规律与隧道内列车压力波的传递规律一致[22]。
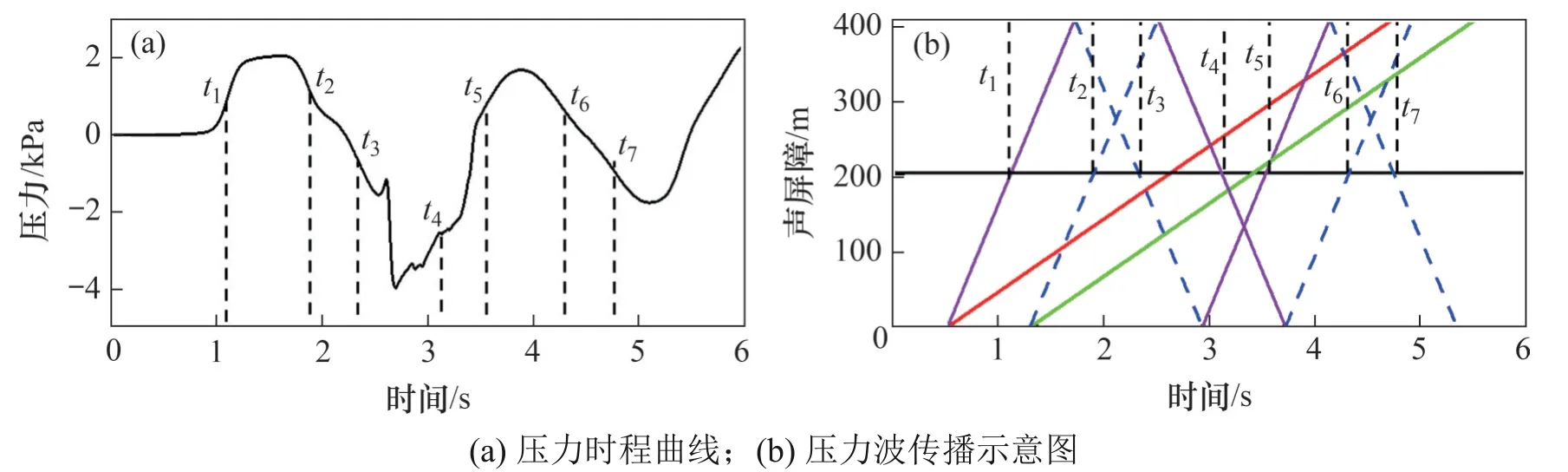
图11 全封闭声屏障S5截面测点压力时程曲线与压力波传播示意图Fig.11 Schematic diagrams of pressure time history curve and pressure wave propagation of measuring point at the central of enclosed sound barrier
声屏障顶部开口后,S5 截面测点压力时程曲线形状发生了改变,正压极值与负压极值减小,风荷载持续时间缩短。随着开口间距增大,当车头经过时,压力迅速上升为正压随即下降为负压;当车尾经过时,压力迅速下降为负压随即上升转变为正压,这与文献[13]实测得到的规律相吻合。在不同开口间距下,声屏障表面风荷载的持续时间见表1。从表1 可见:当开口间距从0 m 增加到2 m 时,风荷载持续时间从5.152 s 缩短为1.740 s,缩短了66.2%。
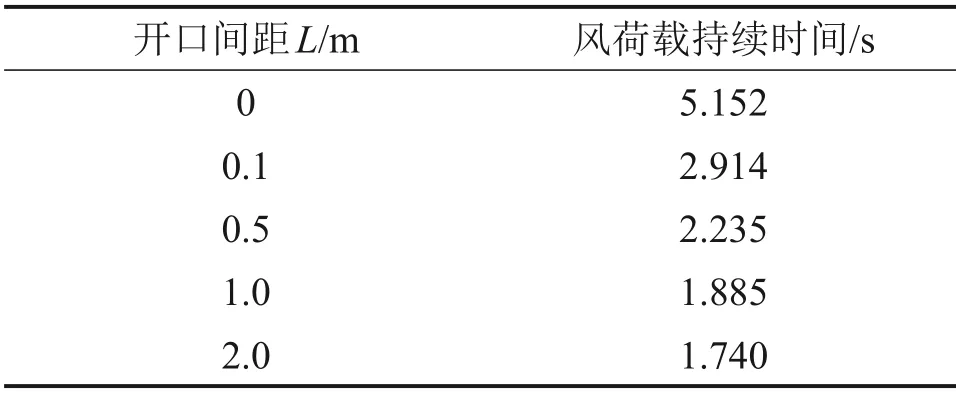
表1 顶部不同开口间距声屏障风荷载持续时间Table 1 Duration of wind loads on sound barriers at different opening spacings
3.3 开口间距对声屏障中间截面极值正压/负压的风荷载环向分布规律的影响
当开口间距L为0,0.1和2.0 m时,S5截面各测点达到正压/负压极值时瞬时的风荷载如图12所示。从图12 可以看出:当声屏障顶部未开口时,S5 截面环向测点的正压极值基本相等,近车侧的负压极值绝对值略大于远车侧负压极值绝对值;当顶部开口间距为0.1 m时,S5截面测点的正压极值沿声屏障环向呈现出明显的不对称性分布,近车侧的压力远高于远车侧的压力,最大和最小正压极值分别出现在P1和P11点,P1点的正压极值比P11点的正压极值高311.9%;当顶部开口间距为2 m 时,S5 截面正压/负压极值沿声屏障环向均呈不对称性分布,最大和最小压力极值同样分别出现在P1和P11点,P1点的正压和负压极值分别比P11点的正压和负压极值高337.8%和600.8%。在顶部开口声屏障的结构设计中,应该考虑截面风压荷载分布的不对称性。
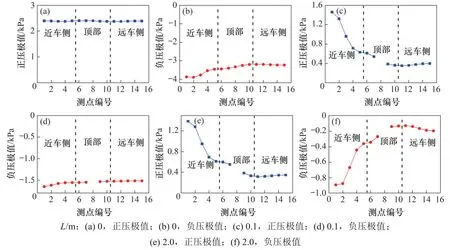
图12 顶部开口间距不同时声屏障产生压力极值时S5截面上的压力分布Fig.12 Pressure distribution on section S5 of sound barrier at different opening spacings when extreme pressure appears
3.4 开口间距对列车车头表面压力的影响
列车在声屏障内运行时,会在邻近的声屏障壁面产生瞬态的列车风致荷载,同样,声屏障的存在也会影响列车表面风压的分布,对列车的运行产生不利影响。当列车通过声屏障时,列车鼻尖的压力时程曲线如图13所示。从图13可知:当列车在明线行驶时(未进入声屏障时),车头压力保持不变;当列车驶入全封闭声屏障时,车头压力迅速升高,声屏障内压力波的传播导致车头压力大幅度变化;当列车驶出全封闭声屏障时,车头压力先下降然后恢复至明线运行时的压力;当声屏障顶部开口0.1 m,列车驶入声屏障时,车头压力迅速升高,随后持续下降,且压力峰值小于全封闭时的压力峰值;当列车驶出声屏障后,车头压力恢复至明线运行时压力;随着开口间距持续增大,各开口间距下列车鼻尖的压力时程曲线变化趋势基本一致;当开口间距为2~8 m时,开口间距的改变对列车鼻尖压力的影响很小。
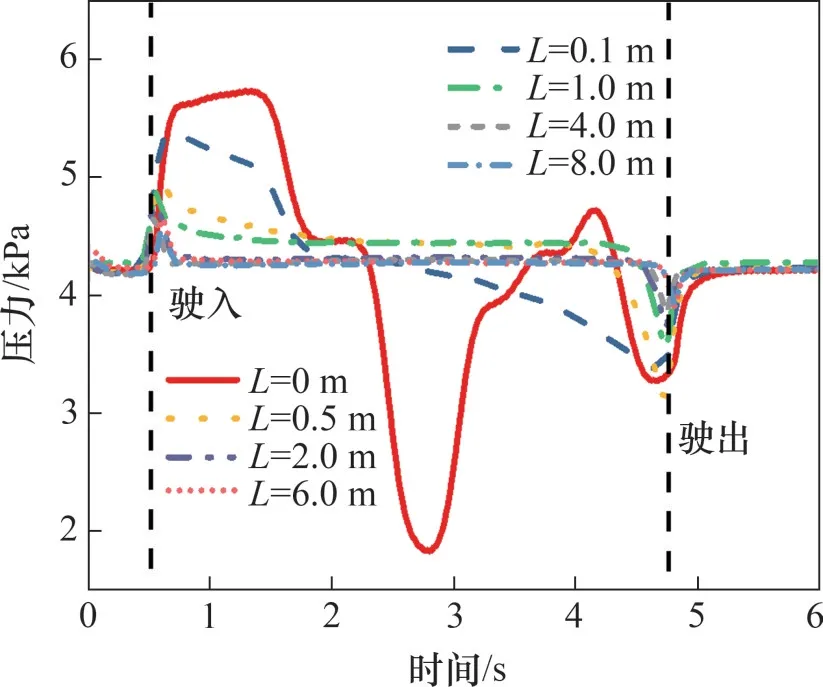
图13 顶部不同开口间距声屏障车头测点的压力时程曲线Fig.13 Pressure time history curves of measuring point on train head of sound barrier at different opening spacings
4 结论
1)当高速列车在全封闭声屏障内行驶时,最大压力峰值出现在中间截面,为5.945 kPa;当声屏障顶部开口后,各截面处的压力峰值逐渐降低;当开口间距为2~8 m时,各截面处的压力峰值相差较小。
2)当高速列车通过全封闭声屏障时,压缩波与膨胀波在声屏障内传播和反射导致同一横截面内的压力变化表现出一定的周期性;当声屏障顶部开口后,压力时程曲线形状发生改变,声屏障表面风荷载的持续时间缩短。
3)对于列车而言,声屏障顶部开口降低了列车前端的空气压缩程度,从而减小了列车鼻尖的压力;当开口间距为2~8 m时,开口间距的改变对列车鼻尖压力影响很小。
