基于频域积分的车体变形量间接获取方法及应用

谢素超，王进，谭鸿创

(1.中南大学轨道交通安全教育部重点实验室，湖南长沙，410075；2.中南大学轨道交通安全关键技术国际合作联合实验室，湖南长沙，410075；3.中南大学轨道交通列车安全保障技术国家地方联合工程研究中心，湖南长沙，410075)

随着高速列车朝着高速化和车体轻量化发展，铁路沿线大风环境对动车组行车安全带来的影响也越来越大，全球范围内已经发生多起行车安全事故，大风给列车行车安全、人民生命安全带来极大威胁[1-3]。且动车组在高速交会和经过隧道或明洞时，由于瞬变交会压力波和截面阻塞比突变引起的气动载荷也会引起车体表面变形，为探究动车组高速行车安全性能，需测量车体受到气动载荷时产生的变形量，分析动车组典型截面的结构刚度，为动车组在铁路沿线高速行驶的安全特性研究提供科学依据[4-6]。在条件允许的情况下，变形量一般都是直接通过位移传感器测量得到[7]。但在运行过程中，动车组车体的振动会使整车产生刚体位移，而车体表面变形主要是受气动载荷作用，体现在瞬时加速度的变化；传统的位移传感器(磁致伸缩位移传感器、拉绳位移传感器和激光位移传感器等)也难以安装在车体表面，不具备安装条件。在这种情况下，本文采用间接测试方法，即通过测量加速度间接得到车体表面位移[8-9]，再减去整车刚体位移获得车体表面变形量。目前，通过加速度信号间接获得位移的方法分为硬件积分法和软件积分法2种。硬件积分法需要的成本较高，且对振动信号处理效果不精确；而软件积分法理论比较成熟，因而得到更广泛的推广应用[10]。在使用软件积分前，需要对加速度信号进行预处理，如：冯坤等[11]采用一种改进的实时双通滤波算法消除低频干扰，解决了积分器不稳定问题；付晓强等[12]利用完备总体平均经验模态分解，消除了趋势项对深立井大药量爆破时近区信号的干扰；薛萍等[13]提出了一种法矢修正的点云数据去噪平滑的算法，具有良好的去噪效果；张芳等[14]对滚筒洗衣机振动信号进行了数据平滑处理，取得了很好的效果。

软件积分分为时域积分和频域积分[15]，时域积分的主要误差来自于累计的趋势项误差[16]。相比于时域积分，更多学者偏向于使用频域积分处理振动信号，如：李智勇[17]提出了基于频域积分的振动信号处理方法，简单实用且精度高；周华[18]采用频域积分对直升机振动信号进行处理，且验证了积分结果的频域特性和误差；成勋等[19]指出频域积分可以将繁琐的积分运算转化为简单的除法运算，提高运算效率，且频域积分相较于时域积分具有更高的准确性和稳定性。

针对以上问题，本文采用最小二乘法消除趋势项，利用五点三次平滑法对曲线进行平滑处理，并设置滤波函数以去除低频和高频噪声信号的影响，对加速度信号采用频域积分方法得到位移信号，通过实验验证积分算法的有效性，并应用于获取和分析动车组车体表面的变形量，为铁路沿线动车组高速行驶的安全特性研究提供科学依据。

1 信号预处理

1.1 消除趋势项

在采集加速度信号时，由于放大器温度变化引起的零点漂移、人为操作失误、样本长度选择不当等会使得采样数据偏离基线，这种采样数据偏离基线随机变化的整个过程称为趋势项。趋势项会直接影响采集信号和积分信号的正确性，因此，需要消除。

趋势项的消除方法有很多种，本文采用常用的多项式最小二乘法[19]，其基本原理如下。

假设采样加速度为{ak},k= 1, 2, …,n，采样间隔为Δt= 1，对于多项式

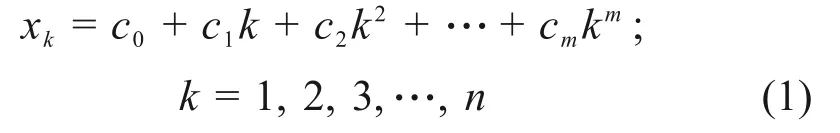
使用待定系数法求得xk的系数cd(d=0, 1, 2,…,m)，使xk与ak的误差平方和E最小，即

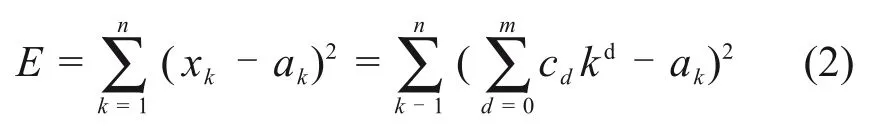
取最小值。E取得最小值。

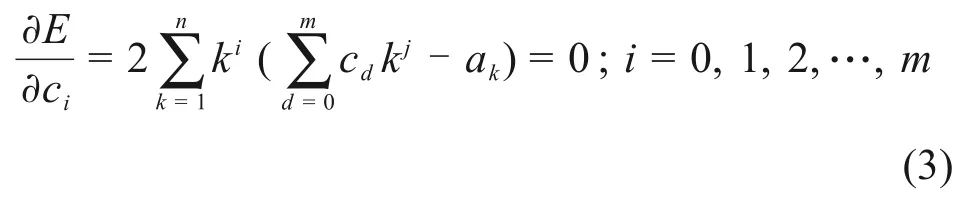
式(3)为(m+ 1)元线性方程组，求解该线性方程组可得满足条件的(m+ 1)个待定系数cd(d=1, 2, 3,…,m)。

带趋势项的原始信号如图1(a)所示，可以看出该信号趋势项随时间不断增大，最后会使信号完全失真。通过最小二乘法消除原始信号趋势项。消除趋势项后的信号如图1(b)所示。通过对比图1(a)和图1(b)可以看出，最小二乘法对于消除原始信号的趋势项具有明显效果。

图1 信号处理前后的对比Fig.1 Signal comparison before and after processing

1.2 平滑处理

受到测试环境和传感器自身干扰等因素的影响，加速度传感器测得的采样信号包含噪声和干扰信号，噪声又包括随机干扰噪声和有规律的干扰噪声，会造成原始数据曲线上出现很多小毛刺，看起来极其不光滑。

为了使原始数据曲线更加光滑，需要对原始数据进行平滑处理，削弱不规则的干扰信号对原始数据的影响，保留原始数据的重要基本特性，提高原始数据曲线的光滑度。常见的数据平滑方法有多种，本文采用五点三次平滑法对原始数据进行平滑处理，使原始数据曲线更加光滑。

五点三次平滑法[7,14]是利用最小二乘法拟合1条直线来计算未知点的函数值，属于一种均值滤波方法。五点三次平滑法的原理较简单，即在相邻的5个数据点中，拟合出1条3次曲线，然后用3次曲线上5个数据点相应位置的函数值作为滤波后结果。基本计算公式为

式中：i= 3, 4, …,m- 2。待处理的原始信号如图2(a)所示，可见曲线上带有很多毛刺。利用五点三次平滑法处理原始信号，经平滑后的信号如图2(b)所示。通对比过平滑前后2条曲线可以看出，平滑处理可以有效去除干扰信号的影响，使曲线更加平滑，波峰值、波谷值的过渡也更加缓和。利用五点三次平滑法处理带毛刺的原始数据曲线，能够有效地去除原始信号中的随机噪声，有较好的拟合效果。

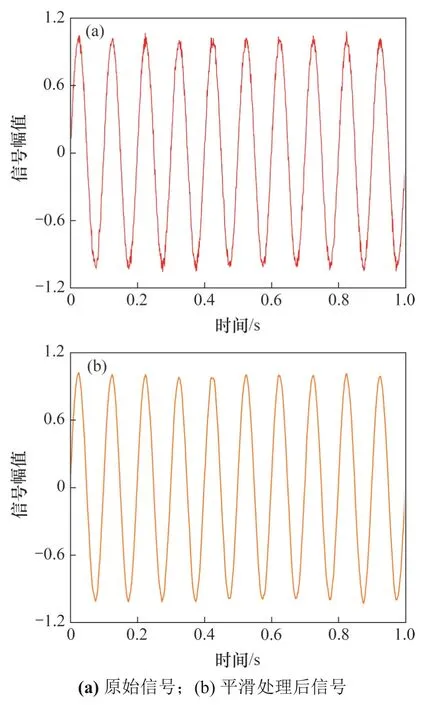
图2 平滑处理前后信号的对比Fig.2 Signal comparison before and after smoothing

2 频域积分

2.1 傅里叶变换

傅里叶变换是一种能够将满足一定条件下的函数关系表示成三角函数(正余弦函数)或者它们的线性组合的转化方法。傅里叶变换的核心就是时域和频域的相互变换，而这种变换是通过一组特殊的正交基实现的，即将直角坐标系中较难表达的曲线通过傅里叶变换在极坐标中简单地表示出来，同样也可以实现逆变换。

设f(t)F(ω)为傅里叶变换的表达形式，根据傅里叶变换的积分定义，有

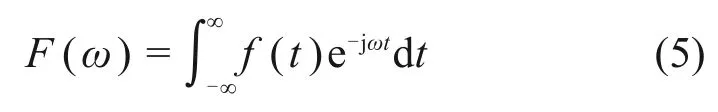
式中：f(t)为F(ω)的象原函数；F(ω)为f(t)的象函数；j为虚数单位，

2.2 数字频域滤波

数字频域滤波[20]是指利用快速傅里叶变换对输入采样数据进行离散傅里叶变换，分析输入信号的频谱，然后，根据相关滤波要求，将需要进行处理的信号值设置成零或加渐变过渡频带后再设置成零。常见的例子有在通带和阻带之间设置一段余弦类窗函数的过渡段，再对滤波后的数据进行离散傅里叶逆变换，得到处理好的时域信号。

数字频域滤波的表达式为

其中，带通滤波器的频响函数为

式中：H(k)为滤波器的频响函数，可确定滤波的方式；X(k)为输入工程信号的傅里叶变换函数；fd为最小截止频率；fu为最大截止频率；Δf为频率分辨率；N为数据点数量。

原始信号与经过数字频域滤波后的信号对比如图3所示，滤波方式为带通滤波，将高于最大截止频率和低于最小截止频率的信号值设置为零，可去除低频趋势项和高频干扰噪声。

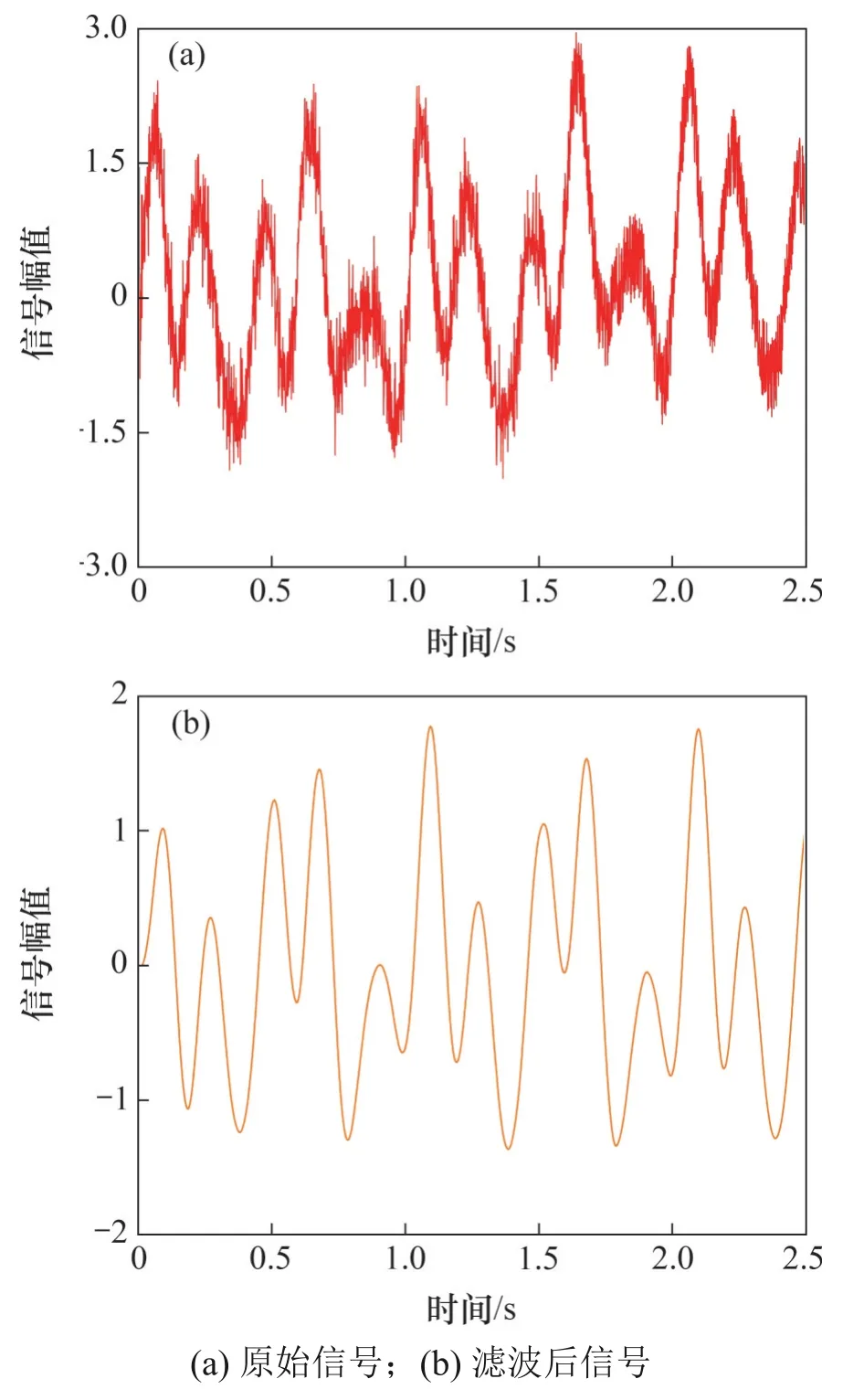
图3 滤波前后信号的对比Fig.3 Signal comparison before and after filtering

2.3 频域积分方法

利用频域积分间接获得位移信号时，先对加速度信号进行傅里叶变换，从而使时域的积分运算变为频域的除法运算，再对积分后的位移信号进行傅里叶逆变换，即可得到时域中的位移信号。频域内积分可以减少时域积分过程中需多次去除趋势项的繁琐流程，也可以降低趋势项带来的累计误差。

根据傅里叶变换公式，加速度信号在某一频率ω的傅里叶分量可以表示成

式中：a(t)为频率ω上的加速度傅里叶分量；A为系数。

当初始量都为0 时，在频域内进行除法运算，即可得到在频率为ω时的速度信号和位移信号的傅里叶分量。计算公式为

完成上述步骤后，再进行傅里叶逆变换，即可得到相应的速度信号分量和位移信号分量。最后将不同频率的傅里叶分量按照式(9)和式(10)进行计算，经过傅里叶逆变换即可得到时域中的速度信号和位移信号。

3 积分算法有效性验证实验

3.1 实验方法

为了验证上述积分算法的有效性，本文在LongDate 电磁吸含式振动台上进行有效性验证实验，通过对比实验采集到的位移信号与加速度信号积分所得的位移信号，验证积分算法的有效性。

高速列车在正常运行过程中，车体的振动主要受到低频激励的影响[21]，因此，本实验将振动台的激振频率设置为0～100 Hz，涵盖了车体典型频谱的峰值频率区间，且振动台最大振幅为10 mm。本次实验共进行4组小实验，采用磁致伸缩位移传感器和单轴加速度传感器分别采集位移信号和加速度信号，位移传感器型号为方易TR-200(量程为200 mm)，加速度传感器型号为朗斯LC-0101E(量程为50g，1g=9.8 m/s2)，位移信号采样频率为1 000 Hz，加速度信号采样频率为25.6 kHz，采样时间为2.5 s，振动台及测试系统如图4所示。

图4 振动台及测试系统Fig.4 Vibration table and test system

3.2 结果分析

对实验中采集的加速度信号进行预处理和频域积分，可以得到积分位移信号，如图5所示。从图5可以看出：积分后的位移信号较平稳，并未因原始信号中的随机噪声和直流分量等因素影响而失去稳定性，说明该积分算法能够有效滤除原始加速度信号中的随机噪声和直流分量。

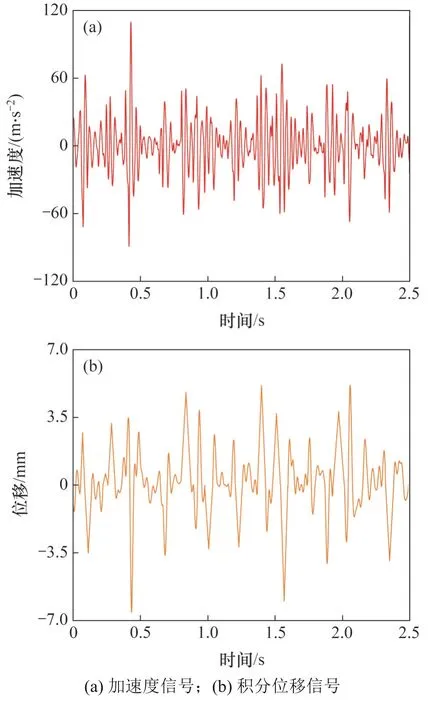
图5 频域积分结果Fig.5 Result of frequency domain integration

由于该方法将应用于实车实验中校核车体刚度，确定车体表面最大变形量是否在许用范围内，因此，在数据分析中更侧重于峰值变化，即主要对积分位移曲线和测试位移曲线的峰值进行对比分析。取4组小实验中前2组的测试位移信号曲线与积分所得位移信号曲线进行对比，如图6 所示。从图6可以看出：积分所得位移信号与测试位移信号峰值基本一致，曲线吻合的程度较高。

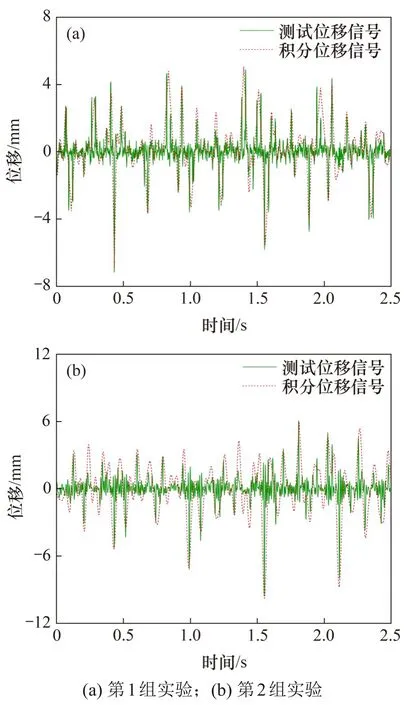
图6 测试位移与积分位移的对比Fig.6 Comparison of test displacementand integral displacement

为了更加准确地对比分析实验结果，用平均峰值误差[22]对4组小实验结果进行评价。误差计算公式为

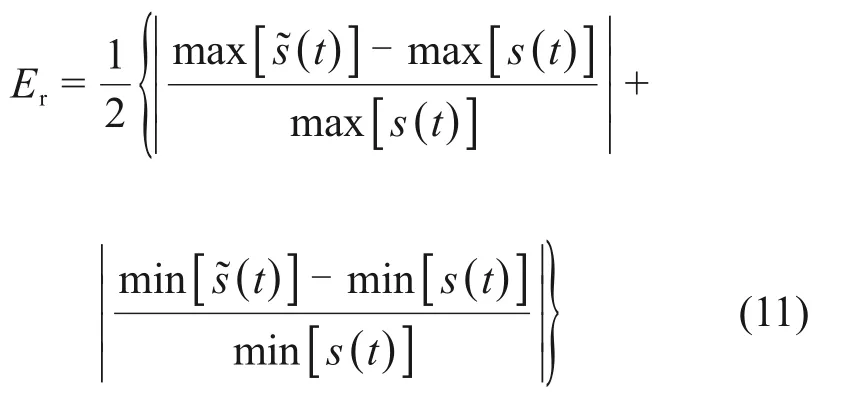
式中：积分位移；s(t)为测试位移；Er为平均峰值误差。

第1～4 组位移平均峰值误差分别为3.98%，2.07%，2.62%和2.53%，这4组实验位移的平均峰值误差均在4%以内，说明积分位移曲线的峰值与测试位移曲线的峰值吻合程度较好，该积分算法能够获得有效位移，可以应用于实车实验中车体变形量的测试。

4 实例分析

4.1 实验介绍

本次实验是对某型动车组在运行过程中1号车和3号车典型截面的车体变形量进行测试，为分析动车组典型截面的变形规律积累数据，并对动车组安全性能进行评估。

在本次实验中，动车组行进方向为下行，在0:00—0:33，动车组时速为200 km/h；在0:34—0:59，动车组时速为210 km/h；在1:00—2：14，动车组时速为220 km/h；且在2:00—2:14，动车组有会车情况。

4.2 实验测试方法

本次测试的主要内容为动车组的车体变形量，测试车厢选取动车组1号车和3号车，车厢具体位置如图7所示。

图7 某型动车组编组Fig.7 A certain type of EMU marshalling

变形测点选择在前端面、中端面及后端面的车体表面，各端面均设置7个变形测点，同时在车内基准测点(1-22，1-23，1-24，3-15和3-16)设置5个加速度传感器，1号车和3号车共布置40个加速度测点，如图8 所示，部分实车实验测点图如图9所示。

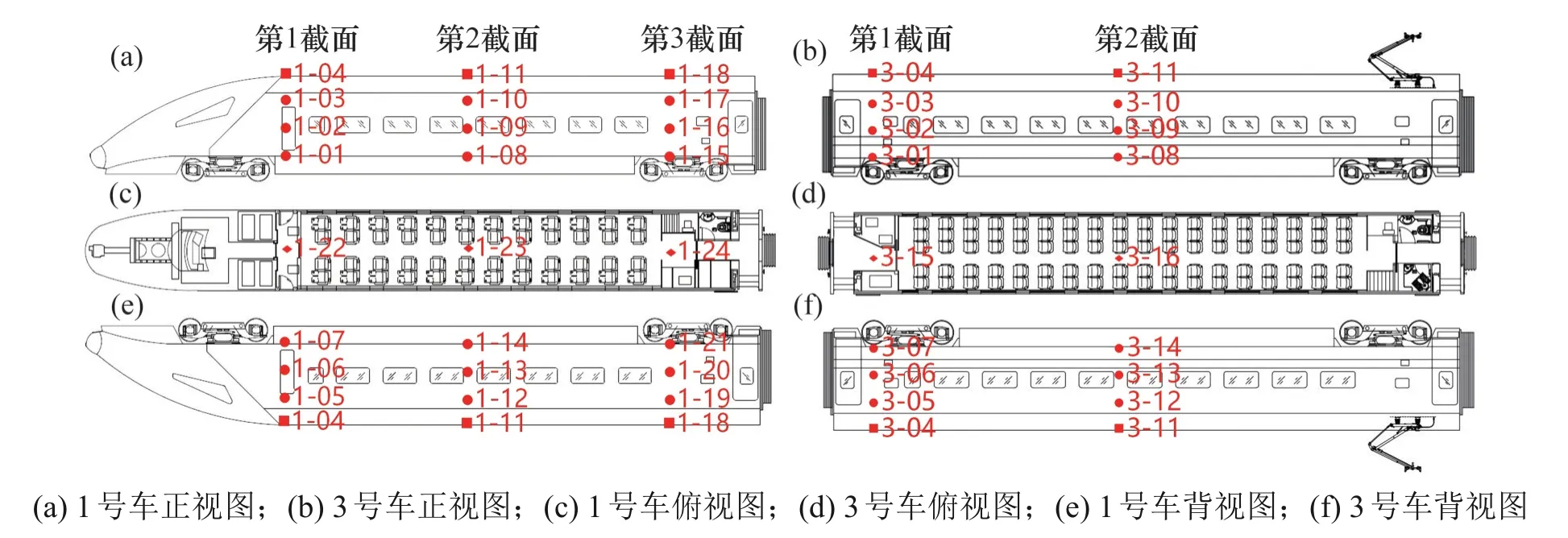
图8 实验测点布置Fig.8 Layout of measuring points

图9 实车实验测点Fig.9 Actual vehicle test points

车内测点加速度信号通过频域内二次积分，可得到车内地板基准相对于轨面的位移变化。车体表面测点加速度信号通过频域内二次积分，可得到测点相对于初始车体表面的位移变化，通过车体表面测点位移姿态与基准位移姿态差分计算，可得到测点相对于地板基准的位移，即测点位置车体表面位移减去刚体位移之后的变形量。

4.3 实验结果分析

本次跟踪实验长度较长，选取了最具代表性的一组测试结果作为分析对象。

对测得的加速度进行信号预处理和频域滤波及积分，可以获得对应位移信号，经整理后可以得到1号车和3号车各截面的最大变形量，如图10所示。

本文中车体变形量反映了一定时间内车体表面变形量。从图10可见：

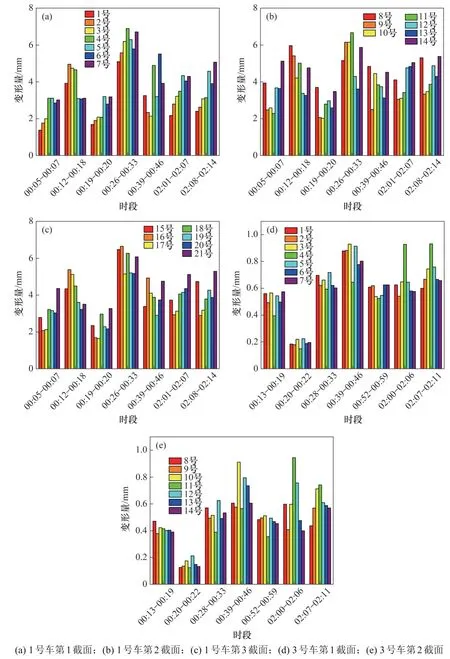
图10 车体截面最大变形Fig.10 Maximum deformation of vehicle body section

1)1 号车典型截面的变形量明显大于3 号车典型截面的变形量，说明1号车受到的气动载荷大于3号车受到的气动载荷。

2)1 号车各典型截面的变形量相差不大，3 号车各典型截面的变形量也相差不大，说明同一节车厢上受到的气动载荷基本上相等。

3)根据TB 1335—1996“铁道车辆强度设计及实验鉴定规范”中车体刚度相关规范，对于整体承载的客车车体，侧墙的相当弯曲刚度为

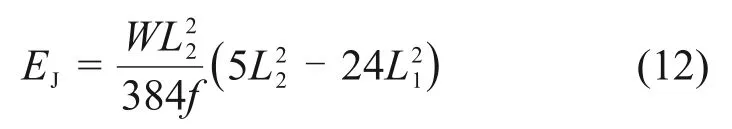
式中：EJ为侧墙相当弯曲刚度，为1.80×109N·m2；W为单位长度载荷；L1为底架外伸部分长度；L2为车辆定距；f为侧墙中央挠度。

对式(12)求解可得侧墙最大中央挠度为15.14 mm。1号车典型截面的最大变形量都控制在8 mm以内，而3号车典型截面的最大变形量控制在1 mm以内，均未超过侧墙最大中央挠度，说明车体典型截面的结构刚度能够满足要求。

4)在2:00—2:14，动车组发生了会车现象，与正常运行时间相比，该时间的车体典型截面最大变形量基本保持一致。

5 结论

1)在测量动车组车体表面变形量时，变形量不易通过位移传感器直接采集，可以通过测量加速度信号后进行积分处理间接获得车体变形量。

2)在对加速度信号进行频域积分前，必须对加速度信号进行预处理，以消除趋势项的影响，达到去除直流分量和随机噪声的目的。基于频域的积分算法可以将繁琐的时域积分运算转化为较简单的除法运算，提高计算效率。实验结果验证了该算法能够获得较好的位移信号。

3)在实车实验中，基于本方法获取了车体变形量，对比分析了动车组典型截面变形量，1号车典型截面的变形量明显大于3号车典型截面的变形量。同一节车厢中各典型截面的变形量相差不大，典型截面结构刚度能够满足要求。

4)由于本方法是通过对加速度信号2次频域积分间接获取变形量，测试结果存在一定误差，目前已通过初步的实验室振动台标定。建议后续细化振动工况，精确模拟轮轨激励条件下的基准振动效应，建立算法实现的真实条件，为车体变形量的间接测量方法提供可参考的理论依据。