基于ABAQUS 的飞机起落架扭力臂拓扑优化分析

苏晓旭

（200093 上海市 上海理工大学）

0 引言

随着航空业的快速发展，最安全、最轻质量、最小体积、结构紧凑的多型号飞机需求日渐增多，对飞机起落系统设计提出了更加严格的要求，对飞机起落架的结构设计、测试要求也更加严格。起落架是飞机起飞、着落、停放和滑跑的重要装置，在整个飞机结构中占据非常重要的位置[1]，其性能直接影响到飞机的起飞着落性能与飞行安全[2]。扭力臂作为起落架中缓冲、减震的关键部件，直接关系到飞机的安全性、平稳性和舒适度。

飞机起落架由扭力臂、连接销、下悬架、上悬架4 个部分组成，如图1 所示。扭力臂和连接销装配件组合如图2 所示。飞机在降落时，起落架上悬架与下悬架发生相对位移，扭力臂相对连接销发生扭转；飞机在地面转弯时，上悬架与下悬架发生相对扭转，此时扭力臂与连接销发生轴向弯曲。针对这两种加载工况，需要对扭力臂进行结构优化。

图1 飞机起落架装配示意图Fig.1 Schematic diagram of aircraft landing gear assembly

图2 扭力臂与连接销装配示意图Fig.2 Schematic diagram of the assembly of torque arm and connecting pin

本文以扭力臂为研究对象，利用ABAQUS 对扭力臂组件进行三维模型建模，并导入进行应力应变分析，利用拓扑优化对扭力臂进行材料分布分析，使用条件算法进行拓扑结构优化。

1 扭力臂初始模型的建立与分析

1.1 扭力臂初始模型的建立

利用ABAQUS 对扭力臂组件进行建模，如图3 所示。该扭力臂组件材料为钛金属，材料密度ρ=4 506 kg/m3，弹性模量E=114 GPa，泊松比υ=0.34，屈服强度σ0.2=461 MPa。使用线性、缩减积分模型划分网格，达到三维应力单元（C3D8R），该单元为连续单元[3]。

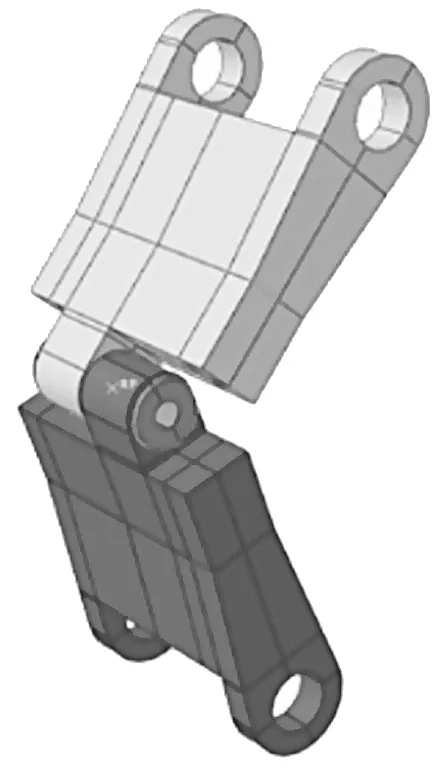
图3 扭力臂组件三维模型Fig.3 Three-dimensional model of torsion arm assembly

1.2 扭力臂静力学分析

起落架扭力臂主要受扭矩作用，在飞机起飞、着落过程中扭力臂受扭矩最大[4]。模型中对扭力臂的两端施加2 个运动耦合约束，连接销部分的连接单元使用刚体约束，扭力臂和连接销定义相互接触。在扭力臂轴孔中施加扭矩6 270 N·m，对其进行应力分析，应力云图如图4 所示。结果显示，扭力臂的最大应力为352 MPa，远远小于扭力臂所用材料的屈服强度461 MPa，故可知该初始扭力臂结构满足其结构强度要求。

图4 扭力臂应力云图Fig.4 Torsion arm stress cloud diagram

2 扭力臂拓扑优化分析

拓扑优化是作为结构设计的一种重要手段，从根本上获得创新的结构形式[5]。拓扑优化的思想是尽可能在保持模型承受载荷部分坚固的同时节省所需要花费的材料，因此优化要求移出模型的多余部分并仍然能够承受相应的预定载荷。在模型设计之初，为了方便后期结构的优化，需要将模型尺寸增大。在对结构进行拓扑过程中，需要应力约束、位置约束和最小尺寸构建的约束。通常可以描述为：

式中：X——结构的拓扑优化变量；xi——拓扑优化中材料的相对密度；f（x）——结构优化的目标函数；x*——优化结果的最值变量；σmax——优化结构单元中的最大应力；[σ]——结构的许用应力；δ——结构施加位移约束点处的挠度；[δ] ——结构的许用挠度。

本文的优化任务是在约束相对体积0.5，即相当于去除50%相对体积的条件下，扭力臂的最大应变能最小，即相当于刚度最大。

2.1 设计变量的选择

拓扑优化是一个在最小化/最大化目标的同时给出约束的材料布局的过程[6]。具体则为一种基于条件的优化情况，如体积约束的情况；去生成相应参数的最优良的拓扑结构，如刚度最优结构。飞机起落架的扭力臂与上悬梁、下悬梁连接的接头和螺栓孔柱位置是重要连接装置，除该区域外皆为设计区域，拓扑优化对设计区域进行结构布局，达到材料分布最优。

2.2 目标函数的设置

目标函数是扭力臂在满足正常约束条件的载荷下，使体积减少50%，满足扭力臂轻量化设计。目标函数输出是扭力臂的最大应力及体积。

2.3 约束的设置

约束条件为在不超过最大应变461 MPa 情况下，优化后的体积低于原设计机构体积50%。

2.4 优化分析设置

多数情况下，扭力臂存在多个复杂的载荷工况，在每个优化迭代中，只对最重要的区域进行分析，应力和应变在分析步中占主要部分。将最大值最小化是优化目标，这里对ABAQU 中设置迭代次数为15，可以查看15 个周期的不同结果。

为了获得更加合理的实际优化效果，建立几何限制。几何限制是对拓扑优化的额外约束，可使优化模型进行对称性约束。为简化优化结果、便于生产，增加几何平面对称性限制。

3 拓扑优化结果与分析

3.1 优化结果

在ABAQUS 中定义好设计区域，在拓扑优化模块Advanced 选项卡中选择Condition-based optimization，基于条件算法获得优化结构。优化后的结果应力体积变化云图如图5、图6 所示。扭力臂在体积减少不低于50%的情况下，应力最大仅337 MPa，依旧小于钛金属的许用应力461 MPa，满足扭力臂受载荷下使用，同时扭力臂的体积也大幅减少。由图6 可以看出优化后扭力臂剩余材料部分体积变化幅度。

图5 扭力臂拓扑优化后应力云图Fig.5 Stress cloud diagram after torsion arm topology optimization

图6 扭力臂拓扑优化后体积变幅Fig.6 Volume change after torsion arm topology optimization

3.2 优化分析

在优化过程中查看模型树不同计算周期中不同的模型结果。如图7 所示，上升曲线为优化刚度曲线，下降曲线为体积约束曲线。可以看出，随着迭代次数的不断增加，扭力臂的体积逐步减少，随之扭力臂的刚度优化效果不断提升，其最大的应变能由之前的352 MPa降低到337 MPa，同比减少4%，但是其体积减少了50%，极大地降低了材料损耗，提高材料利用率。

图7 优化刚度曲线与体积约束曲线Fig.7 Optimized stiffness curve and volume constraint curve

4 结论

通过有限元软件ABAQUS 对起落架扭力臂进行三维建模，施加载荷进行静力学仿真分析，利用ABAQUS 中条件算法对扭力臂结构进行拓扑优化，发现拓扑优化后应力分布得到提高，远远小于材料所需许用应力，说明条件算法的拓扑优化结果满足要求。并且，在承受载荷基本不变的工况下，扭力臂结构材料的体积大幅减少，减轻了扭力臂的质量，达到飞机起落架扭力臂轻量化设计目标。