元胞自动机模拟钢凝固组织演化研究进展

孟祥宁，崔磊，朱苗勇

(1.东北大学多金属共生矿生态化冶金教育部重点实验室，辽宁沈阳，110819；2.东北大学冶金学院，辽宁沈阳，110819)

凝固作为一个跨尺度现象，宏观上涉及热量、质量传输，介观上表现为枝晶与晶粒长大，微观上表现为形核生长。枝晶的形核与生长决定了微观组织形貌，目前主要的检测方法为枝晶腐蚀、断口扫描、电子探针和同步辐射原位观察等，但受成本、应用环境等条件的限制，无法大规模应用于实际生产[1-5]。随着数值模拟技术的高速发展，微观组织模拟已成为当下研究热点，主要方法有格子Boltzmann(LB)法[6-7]、水平集(LS)法[8-9]、相场(PF)法[10-11]、元胞自动机(CA)法[12-16]等，其中，LB法对于静止流体计算效率不高；LS 法计算复杂，图像分割精确度低；PF 法计算效率低，占用内存资源很大。相较于其他模拟方法，CA法具有如下特点：计算速度快，不依赖于单元网格划分结构，同时考虑了形核过程中生长动力学物理机制；在凝固组织微观模拟方面，可以定量反映过冷度与溶质分布对组织的影响；能描述晶粒的尺寸及分布、柱状晶、等轴晶竞争生长以及柱状晶向等轴晶转变(CET)，也可以模拟三维复杂大型铸件凝固组织。因此，CA法被广泛应用于微观组织演化和枝晶生长领域。

CA 法是由Von Neumann 在研究自我复制机制中提出[17-19]，已应用于物理、理论生物学、微观结构建模等多个领域[20-23]。本文从CA 方法原理、特点与应用，并对改进模型模拟组织演化展开论述。在此基础上，概括近年来CA法在钢微观组织演化模拟领域的研究进展，分析其存在的主要问题，并预测未来发展趋势。

1 元胞自动机方法发展

1.1 CA方法简介

自CA 算法提出以来，研究者们对CA 算法进行了不断探索， 特别是20 世纪90年代，MITCHELL 等[24-25]提出并且验证了CA 算法具有随机性和计算不可约性，但并未说明CA具有物理学基础。随后研究者们详细说明了其物理背景[26-29]，CA算法被广泛应用于各个领域，其理论和方法得到了进一步的发展。在计算材料中，CA算法不仅能预测介观尺寸下的晶粒生长，也能对微观尺度下的枝晶形貌进行描述[30]。20 世纪90年代，THÉVOZ 等[31-33]首先将CA 算法应用于凝固组织模拟，采用宏观传热的有限元(FE)模型计算温度场分布，运用动力学方程计算晶粒长大。现在该模型已成为商业软件Procast 软件CA-FE 模块的重要组成部分，被广泛应用于工业生产实际中。SPITTLE等[34]运用CA算法模拟了合金凝固过程枝晶生长和微观偏析，将其从介观尺度模拟拓展至微观尺度。随着CA 算法的不断发展，CA 算法可以用于描述枝晶演化、微观偏析、自然对流和强制对流对枝晶生长的影响以及共晶与包晶凝固等复杂的凝固现象[35-50]。

1.2 CA方法原理

CA算法作为一种全离散动力学模型，不需要建立和求解复杂的微分方程，而是采用最简单的单元化演化规则，便于计算和动态显示[51]。CA 元胞网格划分可以分为三角形、四方形和六边形3种网格，其中，三角形与六边形计算和显示不方便，因此最常使用的是四方网格[52]。CA 算法的基本原理是邻胞布置规则(如图1 所示)，邻胞布置规则有Neumann规则、Moore规则、Margolus规则等，即将计算区域离散为大量元胞组成的网格，元胞状态分为液相胞、固相胞和界面胞3种。建立各元胞与邻胞的之间关系，通过枝晶的生长理论和传输现象求得界面胞的生长速度，近而更新界面胞固相率。当界面胞的状态达到转变要求时，更新界面胞的状态，同时调整邻胞状态，再继续生长捕捉，从而通过简单的演变描述复杂的枝晶生长过程[53]。针对凝固过程的复杂性和CA 界面胞捕捉方式的灵活性，以及采用上述邻胞布置规则产生严重的网格各向异性，学者们提出一种新的界面捕捉规则即修正偏心正方形捕捉规则(MDCS)[36,54]，其捕捉规则如图1(d)所示。该捕捉规则利用一系列枝晶生长方向与对角线方向相同的四方形，辅助实现生长方向与元胞状态的传递。

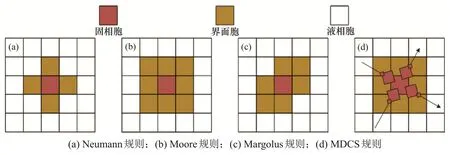
图1 二维CA邻胞类型Fig.1 Neighboring cell in two-dimensional CA approach

2 元胞自动机方法应用

凝固是一个复杂的动态演变过程，很难在实验中实时观测。随着计算机技术的快速发展，国内外学者对CA算法进行了深入研究，它已经成为国际研究的前沿热点。在微观枝晶生长模拟方面，研究者们着眼于界面生长动力学、提出了众多卓有成效的解决方案，从而更为直观地表现枝晶形貌和其生长历程；在介观领域，人们利用模型耦合和界面胞捕捉方法的优化再现了合金凝固过程组织演化[38-42,45-52,54-92]。

2.1 凝固过程模拟

BELTRAN-SANCHEZ 等[88]开发了VFT(virtual front-tracking)机制捕捉界面胞的BSS模型，再现了Al-4%Cu(质量分数)合金等轴晶凝固演化，减少了网格各向异性对枝晶生长的影响，同时验证了BBS 模型计算合金凝固网格的独立性。CHEN等[39,49]利用CA-FE耦合模型预测钨极气体保护弧焊(GTAW)期间晶粒结构的形成。结果表明，在遵循柱状颗粒竞争生长所形成的纹理下，该模型可以处理数百万个晶粒区域。BROWN 等[45]修正了CA模型，可以描述简单共晶系统中的成分对微观组织演变的影响。TAN 等[77]开发了二维CA-PF 耦合模型，预测了Al-Cu-Mg 合金的枝晶生长，模型结果与实验结果吻合良好。CHEN 等[78-80]对CA 模型网格各向异性进行了深入研究，准确模拟单个等轴晶、等轴晶多晶粒生长及定向凝固柱状晶生长，发现枝晶的优先生长方向对于枝晶间的竞争过程具有重要的影响。图2(a)和(b)所示分别为Al-Cu-Mg 三元合金在多晶生长过程中的枝晶形态和微观偏析。孙东科等[56-65]运用CA 法计算了Al-Cu，Al-Cu-Mg和Al-Cu-Mg-Si合金凝固过程中微观枝晶形貌演变以及溶质场分布，并结合计算流体力学模型讨论了强制对流和自然对流对枝晶演变的影响。

图2 枝晶形貌与凝固组织模拟[57,75,80,89,90]Fig.2 Simulation of dendrite morphology and solidification structure[57,75,80,89,90]

随着CA模拟计算的发展，研究者们针对Fe-C合金凝固过程中微观组织模拟展开了研究工作。韩日宏等[89]利用CA模型模拟了Fe-C合金在熔池不同区域中枝晶竞争生长过程，同时，CA模型还可以较为准确地描述凝固过程中的组织演变以及晶间偏析的出现。图2(c)所示为生长方向为25°的等轴晶生长[89]。解决了网格各向异性的问题，发现实际生长角度都与预设的生长取向完全一致，说明所建立的枝晶生长模型可以准确模拟任意取向的枝晶。张蕾等[57]开发了多相CA模型，预测了球墨铸铁凝固过程中奥氏体枝晶和石墨的演变行为与枝晶间气孔形成机理(见图2(d))。LUO等[73-76]将CA算法运用于连铸生产过程枝晶生长，模拟了Fe-0.82C 与Fe-0.6C 合金等温凝固等轴晶与定向凝固柱状晶形貌。WANG 等[75]预测了柱状枝晶的竞争行为，预测的枝晶臂间距接近于测量值(图2(e))。YAMAZAKI[70]在连铸坯有无电磁搅拌下，对其内部晶粒结构演化过程进行了模拟，通过与实验结果比较，验证了模型准确性，同时评估了坯料破碎程度。MICHELIC 等[90]基于CA 算法开发了一个计算Fe-C-Si-Mn-P-S合金凝固过程枝晶微观形貌和溶质分布的模型，计算的合金对象涵盖钢铁材料的主要溶质元素，但忽略了溶质间的相互作用。图2(f)所示为枝晶生长过程中C的溶质场分布，表明该模型不仅描述了从平面前部到树枝状凝固模式过渡，还再现了预期的次级臂。LI等[72]建立一个三元合金枝晶生长的CA模型，给定了界面胞中的固、液相溶质浓度与界面过冷度，描述了Fe-C-Si等轴晶生长。JIA 等[91]建立了一种介观CA 模型，用于研究C-Mn钢在临界退火奥氏体化过程中的微观结构演化和溶质再分布。YAO等[92]利用CA模型对合金磨削强化过程中微观组织演化的动态再结晶过程(DRX)进行了模拟，并与实验结果进行比较，发现该模型可用于模拟合金表面微观结构的动态演化(如图3所示)。

图3 磨削强化过程中再结晶模拟及实验结果[92]Fig.3 Recrystallization simulation and experimental results in grinding hardening[92]

为了更真实和直观地观察再凝固过程中的微观组织演化，研究人员对一些三维CA模型进行了模拟。CHEN 等[79]开发了CA-FDM 模型，预测了Al合金中的柱状晶与等轴晶形貌。从图4(a)～(c)可知：CA模型可以定量反映过冷度与溶质分布对等轴晶形貌演化的影响。由于CA在多组元合金枝晶生长动力学缺乏必要的物理基础，PAN等[63]基于界面各向异性参数与界面固相率之间的梯度，提出了一种界面权值平均曲率的计算方法，并将其应用于三维多取向枝晶生长。图4(d)所示为过冷熔体中等轴晶与定向凝固过程中柱状晶的形貌。此外，研究人员针对Fe-C 合金凝固过程中的三维微观组织模拟开展了研究[42-44,66-69]。ZHAO 等[42]对Fe-1.5%C(质量分数)合金定向凝固过程进行了模拟，得到的枝晶尖端速度和二次枝晶臂间距与实验结果吻合良好，表明该模型可用于模拟实际凝固过程中各种冷却参数下的组织演化。WANG等[66-69]开发了CA-FVM 块修正模型，预测了连铸生产过程中的CET转变，同时还加快了CA法求解速度，使其能够预测大断面连铸坯生产过程产生的中心缺陷。从图4(e)可见：可以清楚地区分辅助臂，随着凝固过程的进行，柱状枝晶不仅与热通量反平行地发展成熔体，而且还以次级臂的形式横向膨胀；在当前的冷却条件下，主分支处的次生枝晶臂可先与其他枝晶臂搭桥，然后因相互竞争生长而变粗。SU等[43]对Fe-1%C-1.5%Cr(质量分数)三元合金钢奥氏体晶粒生长过程进行了模拟，发现该模型可以较好地描述三维不同温度条件下的Fe-1%C-1.5%Cr(质量分数)合金钢的晶粒生长过程。OGAWA 等[44]利用CA 模型再现了Fe-C 合金凝固过程中的多相微观结构演变(如图5 所示)，并考虑了铁素体(δ)、奥氏体(γ)和液相(L)3种相。

图4 三维CA模型下枝晶形貌与凝固组织模拟示意图[63,68,79]Fig.4 Simulation of dendrite morphology and solidification structure under three-dimensional CA model[63,68,79]

图5 Fe-2.1%C(摩尔分数)高渗合金的显微结构形成[44]Fig.5 Microstructures formation of Fe-2.1%C(molar fraction)hyper-peritectic alloy[44]

2.2 夹杂物析出模拟

初始凝固过程直接决定了微观组织均匀性、溶质元素偏析和晶界间低熔点液相膜形成等，极易引起晶界开裂、气孔和局部元素富集等初始缺陷，严重影响钢基体抗变形能力和钢材的最终质量[3,81]。夹杂物的析出可以起到强化铁素基体、细化晶粒的作用，从而提高钢的性能[93,94]。最初对夹杂物析出模拟研究工作主要采用解析模型，PERRARD 等[95]建立了一个Fe-C-Nb 钢铁素体位错上NbC 析出的数学模型(图6)，对形核、生长和粗化规律进行了连续描述；该模型被成功地应用于小角度中子散射获得的大温度范围和2种合金含量的数据集，但该模型仅适用于位错上形成夹杂物的特殊情况。XU 等[96]提出了一种满足元素间Wagner 相互作用、析出物间相互溶解和合金元素守恒等的溶解度限制的高效计算模型，运用该模型计算了钢中氧化物、硫化物、氮化物以及硫化物的析出，还预测了在任何温度下液相、δ 相、γ相以及液相中多组分微合金钢稳定析出物的组分和数量。YOU 等[97]提出了一个耦合微观偏析和ChemSage 数据文件的热力学模型，成功预测了含钛和铝中碳钢夹杂物析出。DEKKERS 等[98]运用Gibbs自由能过饱和度解释了钢中Al2O3夹杂物的形貌和体积随钢液成分的演变过程，但其只对二次精炼钢液中的夹杂物进行了研究，没有分析凝固过程中夹杂物析出演变。IMAGUMBAI 等[99]考虑夹杂物形貌特征，用临界稳定性和扰动理论计算了小过冷度下钢中第二类MnS 夹杂物枝晶尖端半径，提供了用凝固理论方法计算夹杂物形貌的途径。

图6 NbC析出建模示意图[95]Fig.6 Details of NbC Precipitation modelling[95]

有关夹杂物形貌与析出位置模拟模型研究较少，这是因为钢凝固过程中夹杂物析出影响因素较多，需要考虑凝固后期温度场和溶质场分布、夹杂物析出热力学计算。LUO 等[71]利用连铸传热模型和MnS夹杂物析出热力学模型，对U75V钢轨钢大方坯中MnS 大小和分布进行了数值预测(图7(a))，其研究结果表明，对于高硫、粗大组织的连铸大方坯，硫化物夹杂的尺寸要大得多。在夹杂物形貌模拟方面，GAO等[12,82-85]开发了一种跨尺度多元合金CA 模型，该模型耦合第二相粒子(MnS，TiN，CrN，AlN 等)析出热力学及动力学，模拟了Fe 基四元合金中第二相粒子析出，同时解决了枝晶和第二相粒子之间尺度不统一的问题。应用该模型不仅可以计算基体枝晶生长和溶质分布，还能描述第二相粒子形核和生长，从而阐明第二相粒子在钢中的析出机理、形貌演变规律，并探讨钢液成分变化和凝固冷速对钢中第二相粒子析出生长影响。MENG等[83]利用跨尺度CA耦合模型模拟得到MnS 析出形貌和尺寸，如图7(b)所示，可见，MnS 形貌都呈点球状，与OIKAWA等[100]的实验结果(图7(c)和7(d))吻合较好；但二者在形貌上的微小差异说明需要进一步细化CA模型的网格。GAO 等[82]还将MDCS 和非均质成核模型引入CA 模型中，模拟了Fe-C-Ti-N 四元合金柱状晶区与等轴晶区中TiN 的析出演化过程。研究发现，等轴晶区的出现使TiN析出固相率从0.60增加到0.65，柱状晶区的出现使TiN总体积分数减少了70%。这意味着合适的工艺条件可以有效减少溶质偏析导致的铸坯缺陷，提高产品质量，同时，优化了凝固技术，为预测了夹杂物析出情况提供了依据。

图7 MnS演化、Mn溶质分布以及实验结果[71,83,100]Fig.7 MnS precipitation,distribution of solute Mn and experimental results [71,83,100]

3 结语与展望

随着计算机技术的高速发展与普及，CA算法在凝固过程中的应用迎来了新的机遇。采用CA模拟可以动态呈现微观组织演化的形态、分布等特征；有助于理解微观组织的形成机理和控制影响因素。虽然CA算法的应用极大地推动了凝固组织的研究，但CA 模拟的潜力并没有得到充分发挥。主要存在的问题有：

1)Fe-C 合金凝固过程微观组织模拟研究大多使用二维模型，而且在平方毫米级的区域内模拟微观组织变化；为了更真实和直观地再现和预测凝固过程中的微观组织演化，需要开展三维模型及模型二次开发工作。同时算法需要进一步优化，计算效率需进一步提升。

2)模型参数的修正与其准确性的验证有待进一步研究。如何设计合理试验仍是一个需要深入研究的问题。由于材料时空尺度有十几种量级，CA模型的多尺度耦合研究方式成了必然趋势。

3)为了更加真实地反映Fe-C 合金微观组织演变，应考虑各种因素(各种杂质、第二相粒子和多种形核方式等)的影响，夹杂物析出CA 模型还需要考虑凝固后期钢液温度场和溶质场分布、夹杂物析出热力学计算。这些因素严重制约了夹杂物析出模拟研究的发展。

虽然CA模拟在凝固组织演化过程中的应用仍存在一些困难和问题，但随着云计算和大数据的快速发展，其在微观组织模拟领域也将迎来前所未有的机遇：

1)从CA算法的作用和功能来看，对微观组织结构的辅助模拟提供“眼见为实”的确切影像，可以辅助人们透过现象认识本质，解释无法观测的实验现象；对金属力学性能的预测预报提高一个新层次；增材制造等新加工过程模拟涉及快速凝固、液固相转变、组织结构形成与演变等金属学问题，使得CA 算法可以找到用武之地；同时，尝试用CA算法对不同形状、不同性质、不同材料的各类裂纹、空位、位错等进行深入研究，揭示材料缺陷形成与演变的深层规律，有助于提高材料服役期限。

2)CA算法自身也需要向前发展，预期主要发展方向有CA通用软件开发、规则体系扩展、新模型开发以及前后处理功能开发等。经过程序标准化、软件模块化、功能实用化的商业软件开发过程将有望形成理想的CA商业模拟软件，初学者利用CA商业模拟软件可以节省编程调试时间，把更多精力集中在CA 应用创造性工作中。加大新CA机制的开发力度也可以使CA算法成为处理新科学问题的有力工具。前后处理功能开发是对过程记录和再现，对CA 模拟研究非常重要，未来CA 人机界面不但有最终结果，而且还可以获取这些结果的完整过程。