培养高中生数学建模素养的可视化教学

摘  要：数学建模素养是六大数学学科核心素养之一，可视化教学是培养数学建模素养的重要途径. 以三个教学案例为例，阐述如何在日常教学中通过可视化教学培养高中生的数学建模素养，并探索出通过可视化教学培养学生数学建模素养的三条路径：借助问题串，让全章内容体系可视;巧用流程图，让整节研究思路可视;借用思维导图，让思辨思维过程可视.

关键词：思维可视化;数学建模;核心素养

《普通高中数学课程标准（2017年版2020年修订）》（以下简称《标准》）指出，在学习数学和应用数学的过程中，学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养. 数学建模是对现实问题进行数学抽象，用数学语言表达问题，用数学方法构建模型解决问题的素养.

数学建模素养的培养应落实到课堂教学的各个环节. 章建跃博士指出，人教版教材关于数学建模活动的编写思路是：通过加强数学研究对象的抽象过程、加强现实背景的数学化过程、加强数学知识的应用环节、选取适当内容呈现数学建模素养的全过程，有计划地安排数学建模素养的某些环节渗透建模思想. 因此，如何在数学教学的各个环节精心处理教学内容，更好地渗透数学建模思想，成为培养学生数学建模素养的关键.

可视化教学有助于数学建模素养的培养. 所谓可视化教学，其核心是思维可视化，是以文字、图形等形式将教学内容合理整合，让教学内容的呈现更清晰，使原本看不见的思维过程清楚地呈现出来，进而促进知识的深度理解和思维的深度参与的教学形式.

数学思维可视化教学，有利于创造性地处理教材内容、优化教学环节，让学生更好地体会现实背景的数学化过程，更有效地经历数学研究对象的抽象过程，进而促进学生数学建模素养的发展. 下面结合教学实践分享如何在日常教学中运用可视化教学培养学生的数学建模素养.

一、借助问题串，让全章内容体系可视，在核心问题的解决中发展数学建模素养

大单元和核心问题是发展数学建模素养的重要载体. 人教A版《普通高中教科书·数学》每一章的内容体系通常是：实际问题—抽象出数学模型—研究数学模型—解决实际问题. 全章内容围绕一个核心问题展开，在解决问题的过程中需要对现实问题进行数学抽象，并运用数学语言刻画和表达现实问题，最终用数学方法建构模型解决现实问题. 因此，全章内容的学习过程本质上是建立数学模型解决问题的过程. 教学中，要善于利用教学素材，站在全章的角度，引导学生围绕核心问题提出一系列小问题，以问题串的形式，将推动全章内容发展的小问题逐个串联起来，后续内容的学习则围绕问题串中的小问题进行研究，通过解决问题串中的小问题，最终解决全章的核心问题. 问题串为全章内容编织了一张体系网，让全章内容体系可视，为数学建模素养的孕育提供了丰富的土壤.

案例1：“三角函数”章引言课.

（1）创设情境，提出核心问题.

出示以下情境：① 地球自转引起昼夜交替;② 地球公转引起四季更迭;③ 一周七天的循环往复;④ 摩天轮转动过程中，摩天轮上一点的运动.

问题1：以上情境有何共同特征？

生：具有循环往复、周而复始的特征.

师：我们把这种具有循环往复、周而复始特征的变化规律称为周期性.

问题2：如何用数学模型刻画周期性现象？

【设计意图】问题2是“三角函数”一章的核心问题，该问题的解决直接助推本章内容的深入研究.

（2）围绕核心问题，设计问题串.

师：为了用数学模型对周期性现象进行刻画，首先应该找到比较理想的、便于研究的周期性现象. 你能找到这样的周期性现象吗？

学生讨论后，认为可以从熟悉的圆周运动开始研究. 在此基础上，引导学生提问，设计如下问题串.

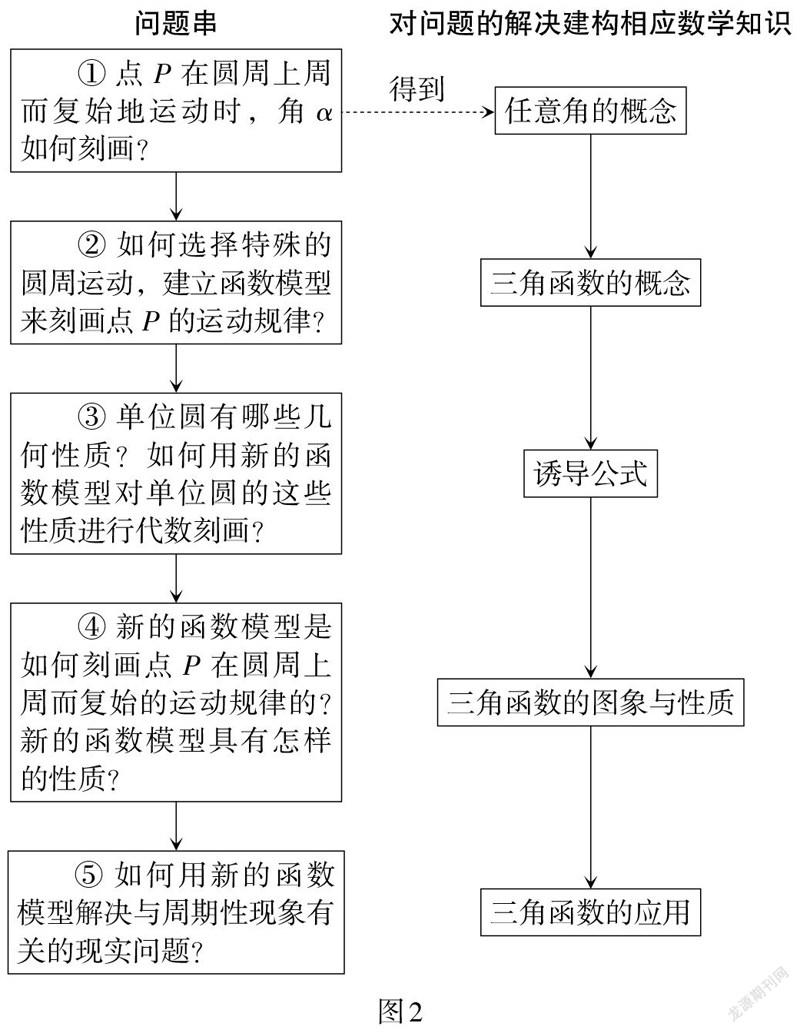
① 如图1，点[P]在圆周上周而复始地运动时，角[α]如何刻画？

② 如何选择特殊的圆周运动，建立函数模型来刻画点[P]的运动规律？

③ 单位圆有哪些几何性质？如何用新的函数模型对单位圆的这些性质进行代数刻画？

④ 新的函数模型是如何刻画点[P]在圆周上周而复始的运动规律的？新的函数模型具有怎样的性质？

⑤ 如何用新的函数模型解决与周期性现象有关的现实问题？

（3）引导学生构建本章可视化的知识体系和研究思路框架.

在本章的后续学习中，引导学生解决上述问题串中的5个小问题. 通过问题的解决，建构全章的主要知识，最终确定本章的知识结构体系和研究思路框架如图2所示.

“三角函数”一章从现实世界中的周期性现象到圆周运动，再到单位圆上点的运动，以单位圆为载体定义三角函数，并借助单位圆研究三角函数的图象与性质. 在此基础上，运用三角函数进一步解决与周期性现象有关的实际问题. 全章内容的建构过程就是建立数学模型刻画周期性现象的过程. 全章从现实世界中的周期性现象出发，提出“如何用数学模型刻画周期性现象？”的核心问题，在该问题的统领下，引导学生提出上述5个小问题，组成问题串. 问题串让本章的知识体系可视化，它直观呈现了本章的研究思路，提纲挈领地展示了全章即将研究的内容，给学生构建了全章的总体框架. 问题串中每个问题的解决直接助推学生将周期性现象抽象为三角函数模型的数学化过程. 学生在经历解决5个小问题的数学活动中，逐步积累用数学语言表达问题和用数学方法构建模型解决问题的经验，并在后续类似问题的思维过程中迁移运用，进而提升数学建模素养.

二、巧用流程图，让整节研究思路可视，在数学概念的生成中培育数学建模素养

概念教学是培养学生数学建模素养的重要契机. 在数学概念的学习中，学生充分体会如何从数学视角将现实问题抽象为数学问题，并建构数学概念解决问题. 在概念的建构过程中，将关键步骤和思考路径记录下来，以流程图的形式呈现. 随着研究的不断深入，逐步完善流程图，让流程图的生成过程成为师生共同建构数学概念的过程. 学生经历数学概念建构的全过程后，在课堂小结中进一步审视流程图，黑板上直观、清晰呈现的流程图让整节课的思维过程清晰可见. 学生借助流程图赏析一节课的精妙之处，回味一节课的探究思路和方法，对数学知识的掌握和数学建模素養的提升都能起到画龙点睛的作用.

案例2：“任意角”的第1课时.

教学流程：列举生活中的周期性现象—指出本章将要学习的新函数（三角函数），并以此来刻画这种周期性现象—从典型的圆周运动开始研究—用角刻画圆周上一点[P]的位置变化—将角的范围扩大到任意角—角的运算—将角放到平面直角坐标系中研究—从特殊到一般得到终边相同的角的集合—用流程图进行课堂小结.

教学过程中，逐步完善流程图，最后呈现流程图如图3所示.

结合上述流程图，引导学生回味本节课的研究思路和研究方法. 为了研究周期性现象，抽象出了圆周运动;为了刻画圆周上一点周而复始的运动，将角推广到了任意角;为了研究的方便，把任意角放到统一的平台——平面直角坐标系中研究，得到了象限角的概念. 在此基础上，从数和形两个角度认识了与角[α]终边相同的角的集合：从数的角度，[α+?k · 360° k∈Z]表示[α]与整数个周角的和;从形的角度，[α+k · 360°?? k∈Z]表示在角[α]的基础上，角[α]的终边转动[k]周. 这样一周一周地转动[k]周正是周而复始的周期性现象，这就是用数学语言表达现实世界.

流程图让“任意角”概念生成过程中蕴含的数学知识、数学知识背后的逻辑联系和数学思想方法清晰地呈现出来，让整节课的研究思路可视. 在数学知识上，可以直观地看出本节课的研究从生活中的周期性现象到任意角，然后将任意角放到平面直角坐标系中研究，得到终边相同的角及其坐标表示;在数学知识背后的逻辑联系上，终边相同的角的集合就是对周期性现象的代数刻画，与周期性现象相呼应;在数学思想方法上，可以感受到从现实问题中抽象出数学问题这种抽象的基本思想和研究终边相同的角的集合的过程中所蕴含的从特殊到一般的研究方法. 通过流程图，学生细细地回味整节课的思维过程，体会其中蕴含的思想方法，挖掘流程图中蕴藏的深意，这有助于学生将实际问题转化为数学问题的思考路径纳入已有的认知结构，有利于学生将如何用数学语言表达和刻画现实问题的思维方式浸入脑海，进而助推数学建模素養的发展.

三、借用思维导图，让思辨思维过程可视，在建模全过程中孕育数学建模素养

数学建模活动是培养学生数学建模素养的直接途径.《标准》将“数学建模活动与数学探究活动”单独作为一条主线，意在让学生通过其他主线内容的学习，积累一定的数学基础知识、必要的数学基本思想方法和建模经验以后，以课题研究的形式用数学眼光观察现实世界，进而提出问题，并抽象出数学问题，确定参数、建立模型、计算求解、改进模型，继而解决实际问题，经历数学建模的全过程.

在数学建模的全过程中，借助思维导图，将隐藏在建模背后的思维过程和思考方法用思维导图直观地展示出来，将建模过程中的思辨思维呈现在思维导图中，可以更好地帮助学生思考，并将思考的方式和路径迁移到其他建模问题的求解中，促进数学建模素养的提升.

案例3：建立数学模型解决茶水最佳饮用时间问题.

情境问题：茶水的口感与茶叶类型和水的温度有关，研究经验表明，某种绿茶用85[°C]的水泡制，在茶水温度降至60[°C]时饮用，口感最佳. 在室温为20[°C]的情况下，刚泡好的茶水需要放置多长时间可以达到最佳口感？

学生经过讨论得出如下解决方法：首先，收集数据;然后，在平面直角坐标系中以时间为横轴、水温为纵轴，作出散点图;最后，根据散点图选择合适的函数模型，求出解析式，并求出函数值为60时，自变量的值.

利用温度计，收集到数据如下表所示.

根据散点图，学生讨论生成三种函数模型选择思路. 根据学生的思路，在课堂上绘制思维导图，如图4所示.

用思维导图将学生建立数学模型解决茶水最佳饮用时间问题的模型选择和改进过程直观地展示出来. 一方面，便于学生在建模过程中进行下一步思考，思考如何对现有模型进行改进，让建模思路更清晰、更有条理，促进学生思维的深度参与;另一方面，便于学生比较各种模型的优、缺点，选择更适合的数学模型，也可以借鉴其他模型在改进过程中的思路和方法，用于改进自己的模型. 例如，思路3的改进1和改进2可以借鉴思路2的改进方法. 通过思维导图，清晰地呈现模型选择和改进过程中隐藏在问题背后的思考路径和思辨过程，有助于将其内化为学生的自觉行为，使学生在后续处理数学问题的过程中不自觉地调用已经内化的思考方法，进而让数学建模素养在思辨思维的运用和建模全过程的体验中自然发展.

可视化教学和数学建模素养的发展应落实在日常教学中，教师要用教学艺术让数学化的过程和数学对象的抽象过程中隐藏在数学活动背后的数学思维可视，继而让数学建模素养在可视化教学中获得更好的发展.

参考文献：

[1]中华人民共和国教育部制定. 普通高中数学课程标准（2017年版2020年修订）[M]. 北京：人民教育出版社，2020.

[2]章建跃，张艳娇，金克勤. 数学建模活动的课程理解、教材设计与教学实施[J]. 中学数学教学参考（上旬），2020（5）：13-19.

[3]张艳娇. 谈“数学建模活动与数学探究活动”如何在教科书中落实：以人教[A]版高中数学教科书为例[J]. 中学数学杂志，2020（9）：1-7.

[4]何承生. 指向高中数学建模的教学实践：“茶水最佳饮用问题”课堂实录与思考[J]. 中学教研（数学），2020（9）：20-23.

[5]张治才. 立足单元高度  凸显数学本质：“单元”视角下的“任意角的三角函数”教学片段分析与反思[J]. 高中数学教与学，2019（4）：28-31.

[6]傅海伦，曾冠予，王彬. 培养高中生数学建模素养的课例及分析[J]. 中学数学杂志，2020（11）：22-27.