基于ARMA模型的股价短期预测——以古井贡酒股票为例

李 易

(华东交通大学，江西 南昌 330013)

随着中国资本市场的发展与开放,股票市场在金融领域中的地位越来越高。股票价格的波动可以作为衡量一个国家经济发展的动态变量,但是其价格的变动通常对时间这一因素尤其敏感,结合理论背景分析,因为时间是股票价格变动的解释变量,所以股价的波动可以看作是典型的时间序列数据。在大多数文献中,研究时间序列所使用的建模方法是自回归移动平均模型(以下简称ARMA)。ARMA模型是一种综合性模型,其特点使ARMA模型所包含的信息更加全面,所解释的信息也更加精确，而且该模型处理平稳的时间序列或者非平稳的时间序列都有较好的效果。因此本文通过建立ARMA模型对古井贡酒的开盘价历史信息进行拟合,并对其未来三天的开盘价进行预测。

一、ARMA模型简介及其建模步骤

(一)ARMA模型的背景知识介绍

ARMA在文献研究中被广泛应用于对时间序列的分析预测,由于大多数经济金融数据满足时间序列的特征,因此该模型尤其适用于研究经济学问题,是拟合满足平稳性约束的时间序列最经典的模型。ARMA 模型是由 AR 自回归过程和 MA 移动平均过程组成的自回归移动平均模型,其基本思想是通过揭示历史时间序列的运行规律,对未来的事物发展进行预测。

在 ARMA(p,q)模型的参数中,p代表自回归部分的滞后阶数,q代表移动平均部分的滞后阶数。通常ARMA(p,q)模型的形式可以表示为:

xt=φ0+φ1Xt-1+…+φpXt-p+εt-θ1εt-1-…-θpεt-p

(1)

其中,{εt}是白噪声序列。AR模型和MA模型都是特殊的ARMA(p,q)模型。当p取值为0时,ARMA(0,q)代表的本质含义就是MA(q);当q取值为0时,ARMA(p,0)代表的本质含义就是AR(p)。但是,如果所要研究的时间序列数据不满足平稳条件的限制,此时便要通过d阶差分等方法使其满足平稳条件的约束,之后才能对此序列进行分析与研究。

(二)ARMA模型的定阶方法

ARMA模型的定阶方法主要是通过观察自相关图与偏自相关图,并且根据其系数的特征显示去选择适合的阶数,如表1所示。对已经满足平稳性要求的时间序列,可以结合相关理论与该时间序列的样本自相关函数和样本偏自相关函数的特征,选择合适的模型与滞后阶数进行参数估计。但是由于样本具有随机性,在现实的时间序列建模实践中情况较为复杂,自相关图与偏自相关图的阶数可能并不会出现完全符合理论的情形,为了选出一个更加合适的模型,这时便要选取可能的阶数建立多个ARMA(p,q)模型,并根据信息准则AIC、SBC、HQ选择三者统计量最小的模型作为确定模型的阶数,构建符合该序列的最优拟合模型。

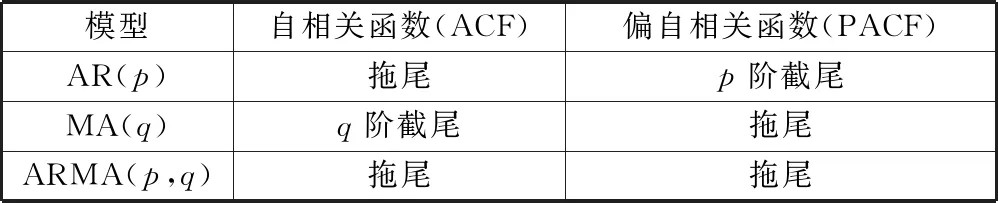
表1 模型特征表

(三)ARMA模型建模步骤

若要深入分析该时间序列数据,首先要确定该时间序列是否满足平稳性条件的约束,因为对于满足平稳性要求的时间序列与不满足平稳性要求的时间序列,所要使用的分析工具是不一样的,本文利用ARMA模型所针对的时间序列必须满足平稳性要求。对于给定的时间序列进行ARMA模型建模,通常步骤如下:

1.平稳性检验。对原序列进行平稳性检验,如果序列不满足平稳性条件,可以通过差分变换或者其他变换方法使该序列满足时间序列平稳性条件的要求。

2.模型的定阶。利用软件计算可以得到描述序列特征的统计量(如自相关系数与偏自相关系数等),之后再通过信息准则等方法确定ARMA模型的滞后阶数p和q。

3.参数的估计与检验。确定好最优模型形式后,通过使用EViews等统计软件进行非线性最小二乘法或极大似然估计法估计计算模型所含有的未知参数,并检验模型参数的t统计量是否满足临界值的标准,以及模型本身的合理性。

4.模型的检验。检验所构建模型的残差序列是否是白噪声序列,可用检验序列相关的方法检验残差序列的纯随机性,或者观察残差序列的自相关图以及偏自相关图。

5.模型的预测。利用经过以上步骤拟合出来的模型预测该时间序列在未来的趋势走向。

二、股票价格预测的实证分析

本文通过Wind数据库选取了古井贡酒(000596)从2020 年 10 月 26 日至 2021 年 9月 21日的股票交易日开盘价数据,共237个样本，运用 EViews 10 软件对此时间序列进行建模分析，并对未来三天股票的开盘价进行预测。

(一)原始数据的平稳化处理

因为影响股价的因素错综复杂,导致股票价格波动较大,故股票价格的时间序列数据往往不能满足平稳性要求,可能需要借助差分、对数化等方法使该序列满足平稳性要求,以便对数据进行后续的深入分析。首先,本文通过EViews 10软件画出原始序列{Y}的时间序列图,如图1所示。由图1可以看出,古井贡酒股票的开盘价原始数据{Y}在这段期间的长期折线图趋势并没有明显规律,短期内波动也比较大,根据折线图可以大致推断出该序列数据可能并不满足平稳性条件。

图1 古井贡酒股票交易日开盘价

为了更加准确地验证其是否满足平稳性,需要对该序列进行ADF单位根检验,由于原始数据并未表现出确定的时间线性趋势,故检验只包含截距项的模型,对该模型进行ADF单位根检验，结果如图2所示。由图2可以看出，在5%的显著性水平下,其p值大于0.05,故原始的时间序列数据不满足平稳性条件。

图2 ADF单位根检验

若要充分判断该时间序列的平稳性,还可以对该时间序列数据的样本自相关图和样本偏自相关图进行观察,如图3所示。由图3可以看出,其相关系数的减弱比较缓慢,因此可以确定该时间序列是非平稳的时间序列。

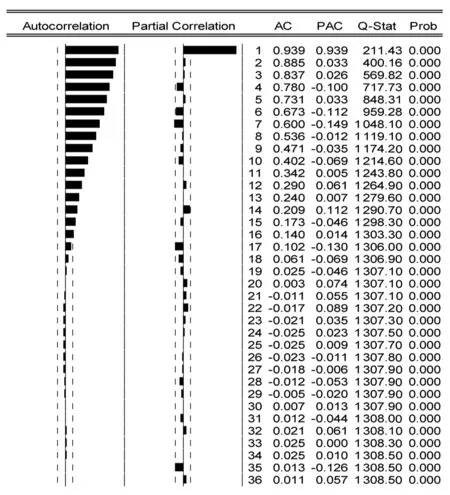
图3 序列{Y}平稳性检验结果

对原始数据的时间序列进行一阶差分处理之后,利用软件画出该差分序列的折线趋势图,如图4所示。由图4可以看出，差分序列的趋势明显比原序列的趋势更加平缓稳定,因此推断出该序列可能属于平稳的时间序列。

图4 一阶差分序列的时间序列图

然而仅通过观察并不能准确判断差分后的时间序列{SY}的平稳性,为了验证其平稳性,分别选择无截距项无趋势项、有截距项无趋势项、有截距项有趋势项进行ADF单位根检验，结果分别如图5、图6、图7所示。可以看出，其ADF test statistic值分别为-16.324 520、-16.290 650和-16.273 490,p值分别为0.000 0、0.000 0、0.000 0,经分析发现三种情况的单位根检验的p值均小于 0.05,拒绝原假设。因此,需要通过利用最小的AIC、SC、HQ值判断哪种模型最合适。无截距项无趋势项的AIC、SC、HQ值分别为6.948 229、6.962 951、6.954 164;有截距项无趋势项的AIC、SC、HQ值分别为6.956 671、6.986 114、6.968 541;有截距项有趋势项的AIC、SC、HQ值分别为6.964 013、7.008 178、6.981 818。经过判断,综合三个模型的AIC、SC、HQ值会发现，无截距项无趋势项模型的AIC、SC、HQ值比较是最小的,因此选择无截距项无趋势项的模型。

图5 无截距项无趋势项的ADF单位根检验

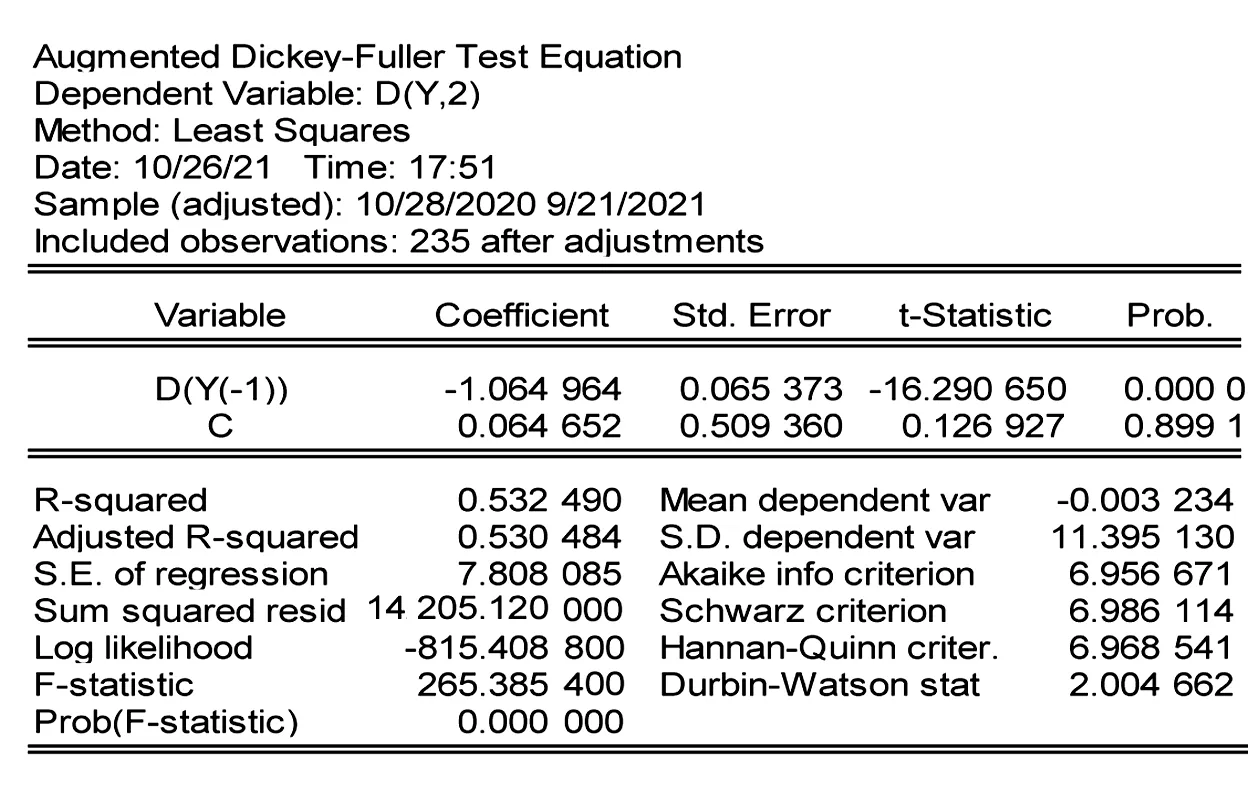
图6 有截距项无趋势项的ADF单位根检验

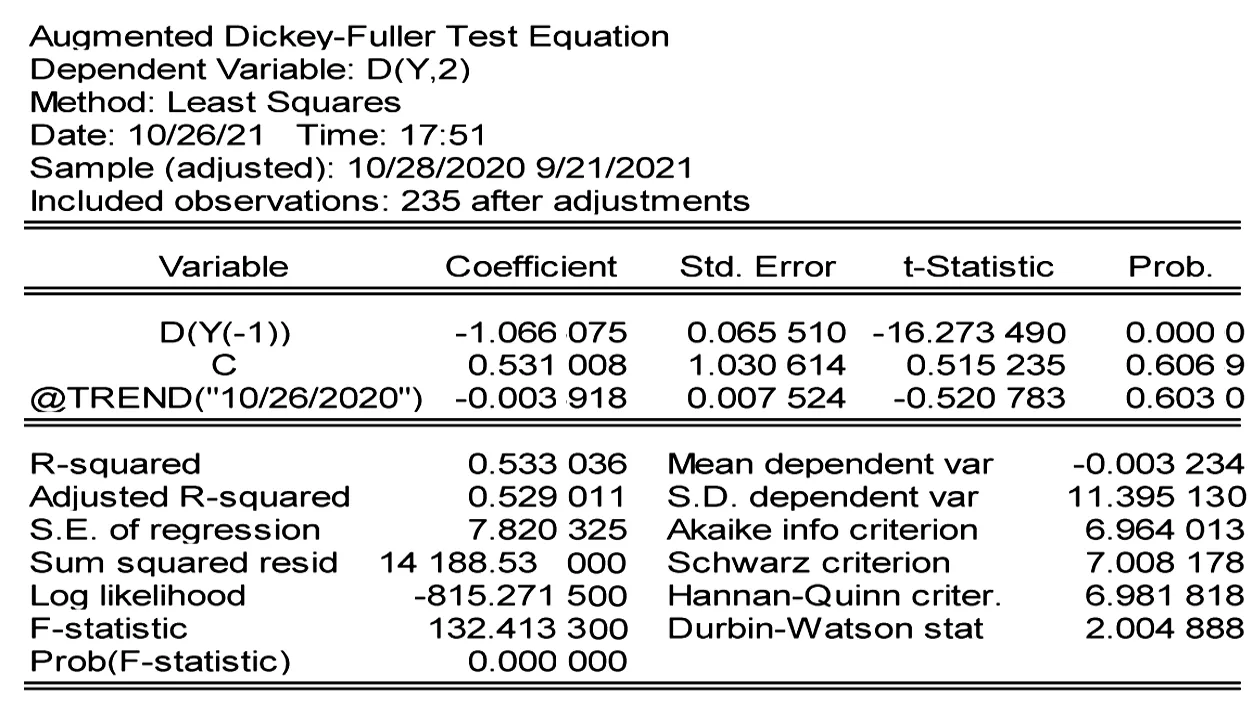
图7 有截距项有趋势项的ADF单位根检验

(二)对模型的识别

一阶差分后的时间序列{SY}的样本自相关图和样本的偏自相关图两者都没有截尾特征,因此满足ARMA建模的定义条件。但如果要获取准确的滞后阶数p和q的值,还需要利用AIC信息准则、SC信息准则和t统计量进行具体判断，如图8所示。

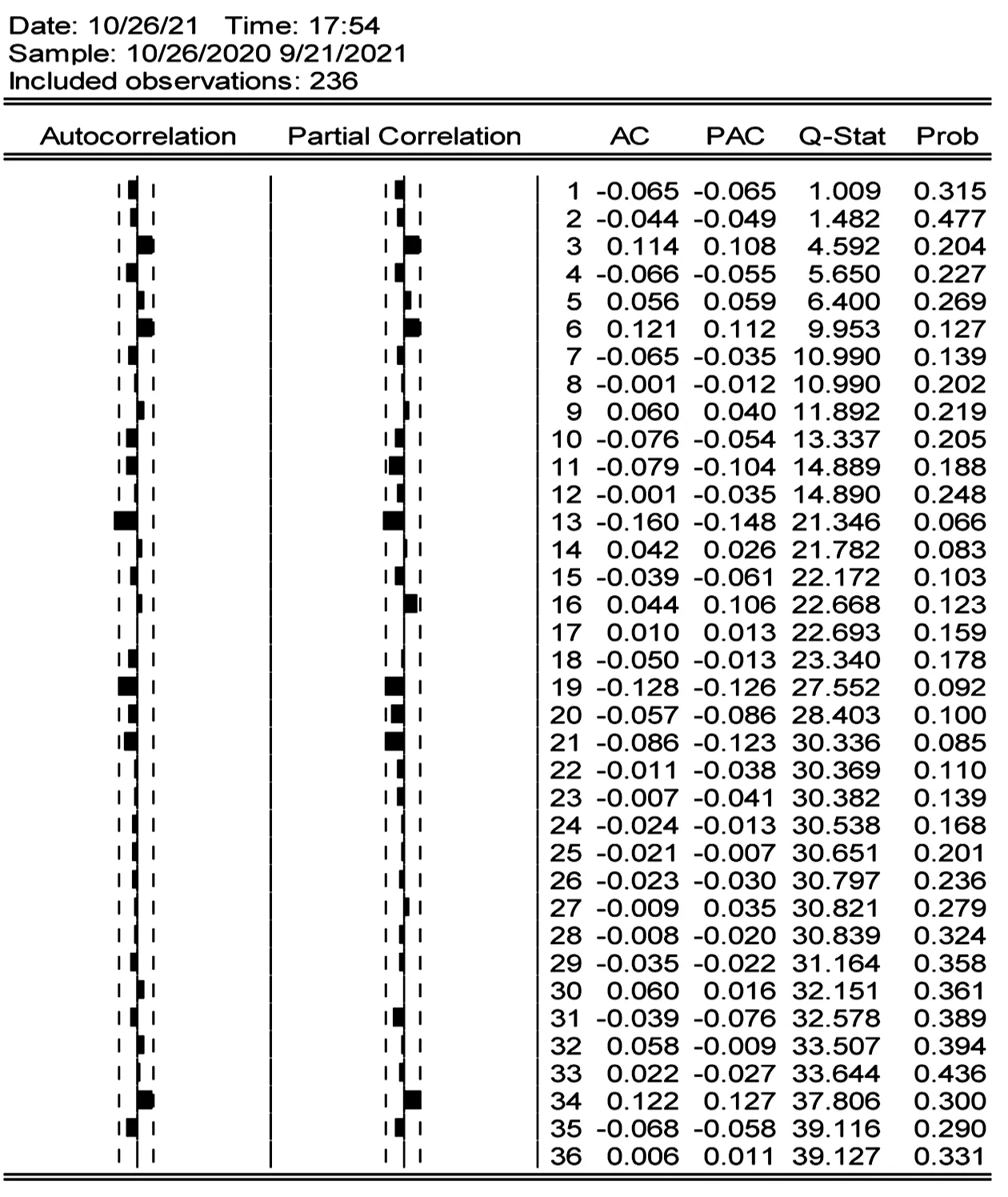
图8 序列{SY}的样本自相关图和样本偏自相关图

根据以往的实证经验可以得知,大多数金融与经济变量的模型满足p值与q值都≤2的分析模型,由于该序列是一阶差分后的时间序列,故I取值为1。因此本文选取模型阶数覆盖p≤2和q≤2的共4种模型进行比较,以判断最佳的模型阶数。这4种模型分别为ARIMA(1,1,1)、 ARIMA(1,1,2)、ARIMA(2,1,1)、ARIMA(2,1,2)。

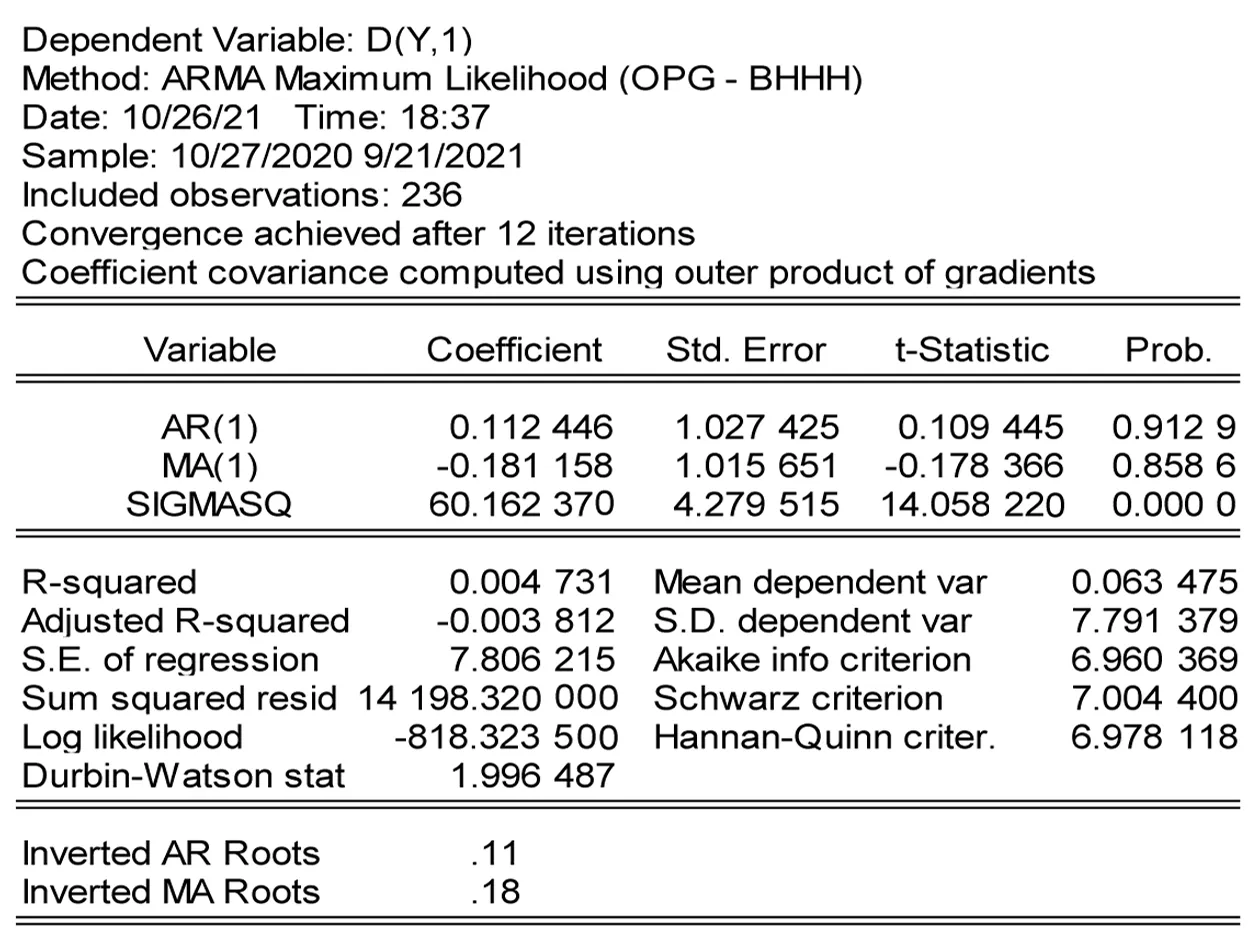
选择考察变量为一阶差分后的序列数据,考察样本的范围为2020年10月26日至2021年9月21日。综合不同滞后期模型的t统计量与信息准则AIC值、SC值、HQ值等多项检验指标,对比模型各个统计量的标准临界值。经比较得出:ARIMA(2,1,2)模型中AR(1)、AR(2)和MA(1)、MA(2)的系数表现都尤其显著,并且此模型的AIC值、SC值、HQ值都相对较小,结合信息准则等方法,选择ARIMA(2,1,2)模型作为该序列的最优模型，如图9所示。

ARIMA(1,1,1)

(三)开盘价序列模型的建立与参数估计

根据以上一系列检验判定,选择 ARIMA(2,1,2)模型作为最佳预测模型,对该模型的各项参数进行估计计算,如图10所示。根据图10结果,模型 ARIMA(2,1,2)的各项参数对应的p值全部为0,小于0.05,该模型参数显著有效。根据参数估计,可以写出模型的表达式为:

图10 模型系数图

Yt=-0.084Yt-1+0.217Yt-2+0.867Yt-3+εt+0.772εt-1+1.031εt-2

(2)

其中{εt}为残差序列。

(四)开盘价序列模型的残差检验

完成上述参数估计步骤后,最关键的步骤就是要对该拟合模型的残差序列进行检验,观察其是否满足白噪声的定义条件,因为只有该模型的残差序列为白噪声,才可说明构建的ARMA模型已经把该序列的关联信息都提取出来了。白噪声过程的特点在于其纯随机:各个时期的随机变量没有相关性,该随机性说明已经没有足够的关联信息来支撑模型构建。因此，可以把白噪声序列特殊的性质作为判断此拟合模型是否构建合理的标准。若发现该残差序列各个时期的随机变量仍具有相关性,代表该残差序列仍含有相关信息,说明需要继续改进构建的ARMA模型;如果残差序列是白噪声序列,则说明构建的ARMA模型已经把关联信息都提取出来了。对残差序列进行白噪声检验结果如图11所示。由图11可以看出，p值对应列所显示的概率值全部大于0.05,表明不拒绝残差为纯随机序列的原假设,意味着残差中不再包含该时间序列的关联信息。故推断出所构建的ARIMA(2,1,2)模型可以提取该时间序列数据的全部关联信息,可以作为模拟古井贡酒股票开盘价发展规律的最优模型。

图11 残差序列的自相关图和偏自相关图

(五)对开盘价序列进行预测分析

使用最优模型对2020年10月26日至2021年9月21日的数据进行拟合,比较拟合值与输入的真实值并绘制折线图，如图12所示。由图12可以看出，实际值{Y}与预测值{YF}趋势高度相似,模拟效果良好。

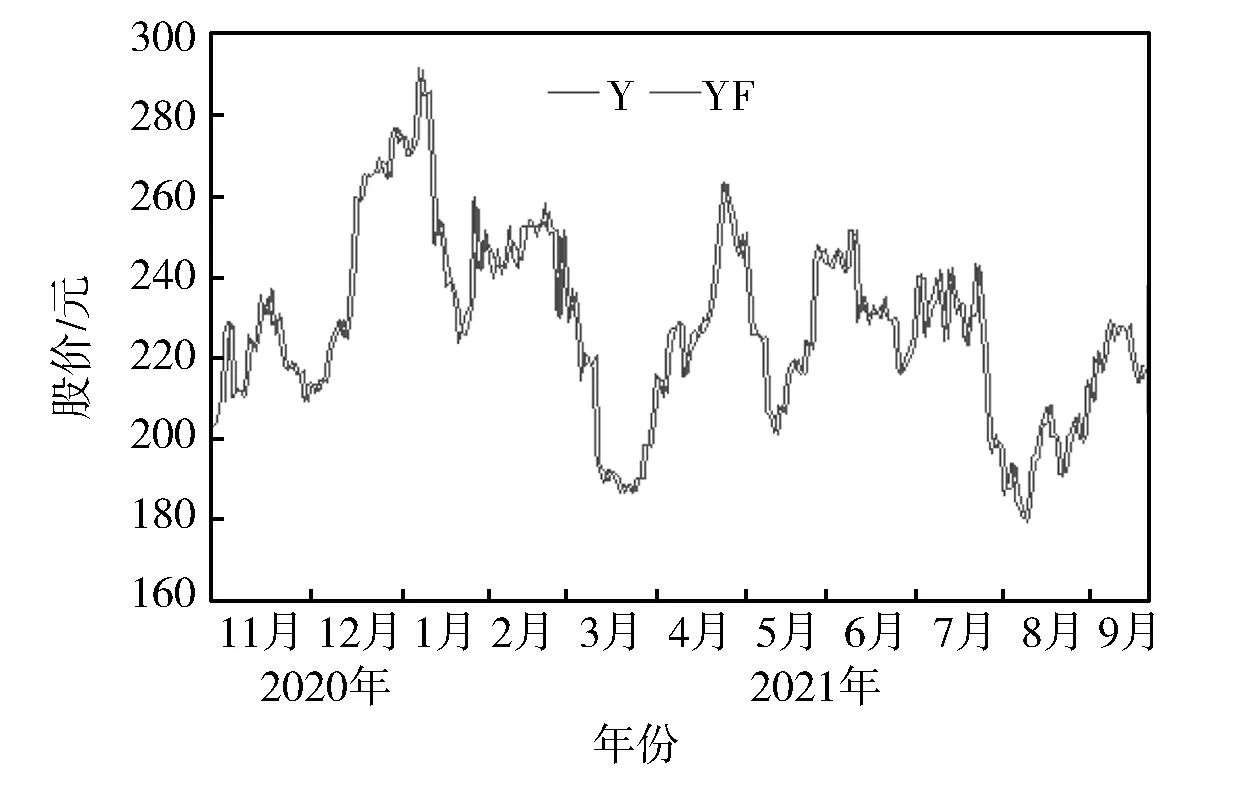
图12 序列{Y}和序列{YF}的时间序列图

利用所构建的ARMA模型对古井贡酒股票的日开盘价进行预测,短期内得到的结果较为精确;但是由于投资者预期、政府出台的政策以及公司自身所具有的非系统性风险等因素都会干扰股票价格的走势波动,故长期预测的结果误差比较大。所以本文只是对股票价格波动做出较短期限内的预测,预测2021年9月22日至2021年9月24日的开盘价,如表2所示。

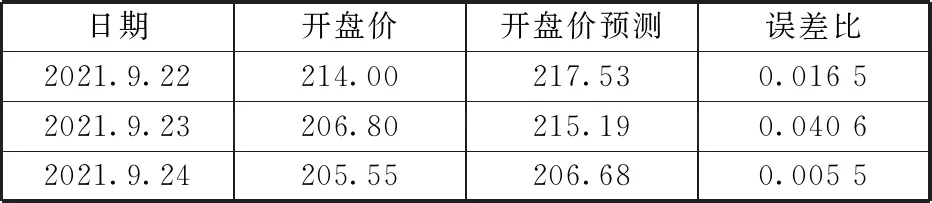
表2 开盘价与预测价结果

由表2可以看出,使用该模型预测得到的古井贡酒股票2021年9月22日至2021年9月24日的开盘价分别为217.53,215.19,206.68,误差比分别为0.016 5,0.040 6,0.005 5。不难发现,预测值和实际值之间的误差比相对较小。由此也进一步验证了本文建立的模型是较为准确的,对古井贡酒股票日开盘价的预测相对准确。

三、结语

本文通过应用于时间序列分析的ARMA模型对古井贡酒(000596)股票的开盘价进行实证分析,在此基础上使用所建立的最优ARMA模型对其未来三天的开盘价进行预测。

首先,针对选取的原始数据制作趋势图后发现，该原始数据具有下降的长期趋势,并在短期内呈现不断波动的特点。根据趋势图的走势可以大致分析出，该时间序列数据并非一组平稳的时间序列数据,故随后对该数据进行差分处理以使该序列满足平稳性条件的要求。其次,根据一阶差分后数据的自相关图与偏自相关图,结合信息准则AIC、SC、HQ，t统计量等相关统计量对该模型进行阶数与系数的估计确定,并根据最终估计出的相关系数写出该模型的表达式。再次，通过对该模型的残差序列进行检验,判断其是否满足白噪声序列的性质,从而判断该模型的建模是否适用于预测未来的股价趋势。最后,通过该模型对古井贡酒开盘价进行预测并与实际值进行比较,由于预测走势图与实际走势图的拟合程度非常高,所以该模型在短期内的预测效果优良。

综上所述,ARMA模型确实是分析预测时间序列的一种有效的工具方法,可以将其应用在经济金融投资领域中,对中小投资者的短期投资活动提供较为科学的参考价值。但是,股票价格的时间序列是非平稳的时间序列,因此对其进行差分后可能会损失很多重要信息,而且股票价格的长期趋势受到外部冲击的影响较大，如国际趋势变化、国内政策变化等各种不确定因素都会干扰股票价格的变动，而短期预测受到干扰因素的影响较小。因此ARMA模型只是适用于短期预测,并不能精确拟合股票价格的长期趋势。要想分析预测变量的长期变化,还需要设计更加精确、细致的模型。