曲线系视角下的直线过定点问题*

中山市桂山中学(528463)刘丹峰

广东省五邑大学(529020)王喜建

解析几何中动直线过定点问题是高考中常考的类型题,以近五全国卷为例,在2017年、2018年以及2020年这三年的考查方向均为直线过定点问题的正向或逆向考查.所不同的是题中的主干条件或所推结论或是斜率之和为定值关系,或是斜率之积为定值关系.文[1-2]均对这两种情况作了推广得出一般化的结论,然而均是对和与积关系的独立分析,论证中均是通过斜率和或积的定值关系去构建关于动直线的斜率与截距之间的等量关系,从而得到直线过定点.值得思考的是,若题中所给条件兼有和积关系,动直线是否还有过定点的性质呢? 本文通过对浙江省杭州市第二中学一道周末练习题的逐步深入分析,引入曲线系概念,旨在综合分析这一模型,以期能将问题模型更加一般化.

一、似曾相识燕归来

二、柳暗花明又一村

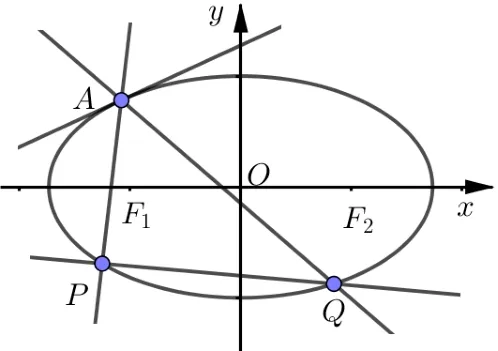
不难发现以上两种方法计算都非常繁杂,计算核心难点在于直线AP,AQ与动圆相切所得到的关系式21(k1+k2)+ 20k1k2-20 = 0 相对于所列的高考题更为复杂.考虑到这一点,笔者引入曲线系的概念和方法来处理,以图减少计算量.基于本文模型,给出如下曲线系概念.如图所示,设二次曲线方程为f(x,y)= 0,A为曲线上一点,直线l为曲线在点A处的切线,过点A的两条直线l1,l2与曲线交于P,Q,记直线PQ为l3,显然,A,P,Q三点坐标均能使得方程ll3+λl1l2= 0 成立(这里的l,li表示直线方程非零端),则过A,P,Q点的二次曲线系方程可表示为ll3+λl1l2=0.

三、举网以纲,千目皆张

由文[1-2]可知,当过曲线上一点的两条直线,若两斜率之和为定值,则PQ过定点;若斜率之积为定值,则PQ亦过定点.而在该题中,由直线AP,AQ与动圆相切所得到的关系式21(k1+k2)+20k1k2-20 = 0 中既有斜率之和,又有斜率之积,和与积之间满足一个线性关系式,此时亦有过定点的性质,这是该题的巧合还是性质使然.为此笔者提出下述定理,并对其加以证明,以探求该题模型背后的意义.

定理不失一般性,假设曲线C:mx2+ny2= 1,点A(x0,y0)为曲线上的任意一点,过点A作斜率分别为k1,k2两条直线交曲线于P,Q,若k1,k2满足p(k1+k2)+qk1k2+r=0,则直线PQ经过定点

证明设直线PQ的方程为y=kx+b,过点A(x0,y0)的切线为l,则l的方程为mx0x+ny0y-1 = 0 由题可知AP:y-y0=k1(x-x0),AQ:y-y0=k2(x-x0),则过点A,P,Q的曲线系方程可表示为l·lPQ+λlAP ·lAQ= 0,代入直线方程可得:(ny0y+mx0x-1)(y-kx-b)+λ(y-k1x+k1x0-y0)(y-k2x+k2x0-y0)=0,整理可得:

由此我们论证了,只要斜率的和与积之间满足一个线性关系式,直线便会经过定点.所得推论中,由参数的不同取值,再次证明和与积分别为定值时,直线所过定点坐标与题干参数之间的关系,并得到斜率的倒数之和为定值时,亦能得到直线过定点的性质,可谓“举网以纲,千目皆张”.

四、不畏浮云遮望眼

基于以上所得定理及其推论,下面给出相对应问题用以说明其应用