极点极线背景试题的计算策略
2022-03-25湖北省天门中学431700代成红
湖北省天门中学(431700)代成红
以极点极线为背景的试题在中学各级考试中屡见不鲜.这一类问题往往算法复杂、计算困难.在教学实践中,笔者总结了一些处理极点极线背景试题的计算策略,现在写出来,求教于方家.
一、设线策略
以极点极线为背景的试题考查的主要是直线与圆锥曲线的位置关系,所以设线策略(设直线方程并与圆锥曲线方程联立求解)依然是我们解题中的首选策略.但设线策略在计算过程中经常会用到韦达定理,自然需要计算式子是对称的.如果计算过程中出现不对称的情况,可以采用以下策略.
(一)同构方程策略
解析几何中,分析图形是设计算法的基石.理清图形含有的元素(点、直线、圆锥曲线)以及它们的相互关系是分析图形的出发点.如果图形中有两个点从元素间相互关系来看,地位相同,我们围绕其中一个建立等式,另一个同理可得相似的等式,此时就可以构造方程,简化计算,提高运算效率.
例1(2020年高考北京卷第20 题)已知椭圆C:过点A(-2,-1),且a=2b.
(1)求椭圆C的方程;
(2)过点B(-4,0)的直线l交椭圆C于点M、N,直线MA、NA分别交直线x=-4 于点P、Q,求的值.
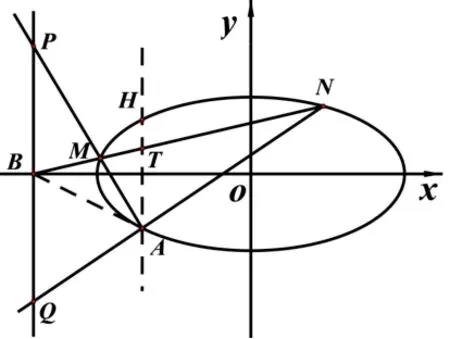
图2
分析常规设线法首先是联立直线MN与椭圆C方程,得到点M,N的纵坐标yM,yN的关系,然后将点P,Q的纵坐标yP,yQ用yM,yN表示,再消去参数yM,yN算出答案.但是在直线MN与椭圆C的相交关系中,点M、点N地位相同,这是容易计算出对称式yM+yN,yMyN的原因;图1中点P、点Q是直线x=-4 与两条不同直线MA,NA相交而成,地位并不相同,这是在计算yP,yQ的比值时,算出yM,yN非对称式的原因.处理非对称式需要一定运算技巧,运算量大,是常规设线法难点所在.
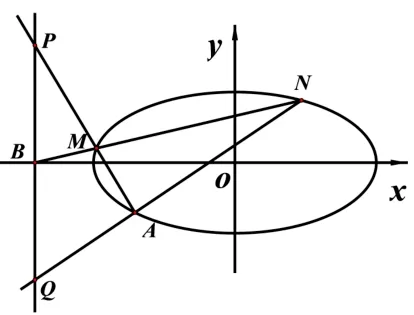
图1
如果仔细分析图1 中六个点以及它们与其它元素的关系,可以发现:点M是椭圆与直线MN、PA的公共点,点N是椭圆与直线MN、QA的公共点,它们的地位相同.如果我们以点M代入椭圆方程得到一个等式,用点N同理可得到完全类似的等式,从而可以构造二次方程,使用韦达定理.这样处理,回避了非对称式,极大地减少运算量.

分析图3 中包含一个椭圆,四条直线,六个点,从它们相互关系来看,点A是两直线MA、AB与椭圆的公共点,点B是两直线MB、AB与椭圆的公共点,地位是相同的,因此可从点A、B入手构造同构方程来简化计算,提高运算效率.

图3

图4


(二)非对称式消元策略
当用设线法求解极点极线背景试题时,很容易碰到计算非对称式的情形.在这种情形下,最直接的思路是消元.只不过在消元的时候一是要打破思维桎梏,敢于把使用韦达定理得到的对称式拆开;二是消元前根据解题要求确定好消那个元,一消到底.

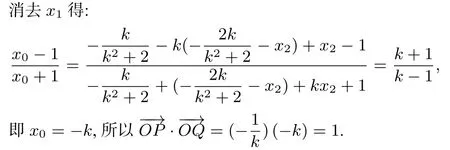
评注①如图5,点Q在点P的极线xP x= 1 上,因此②在例3 中,因为xP与k有关,因此计算x0时应保留k继续参与运算,所以选择消去x1(或x2),消元时要敢于破坏x1+x2的对称性,将x2(或x1)一消到底,留下x1(或x2),k进行运算.
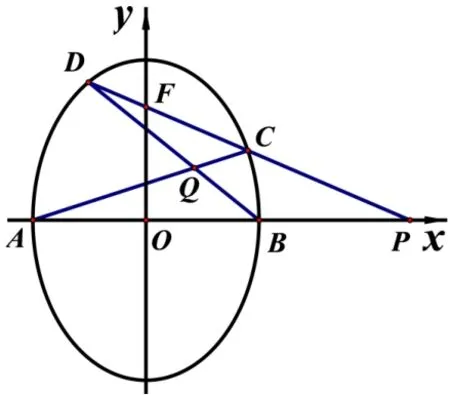
图5
(三)非对称式转化为对称式策略
在很多极点极线为背景的试题中,遇到计算非对称式的情况,可以先分析图形中的各个元素,寻找它们之间的数量关系,如果能利用这些关系将非对称的式子转化成对称的式子,就可以用常规的方法解决问题了.
例4(2020年高考全国卷Ⅰ理科第20 题)已知A、B分别是椭圆E:1(a >1)的左、右顶点,G为E的上顶点,为直线x=6 上的动点,PA与E的另一个交点为C,PB与E的另一个交点为D.(1)求E的方程;(2)证明:直线CD过定点.
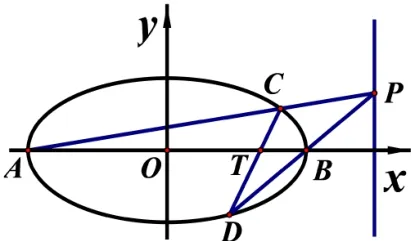
图6


二、设点策略
设线策略在进行计算时,直线与圆锥曲线的交点总是成对出现,单独计算其中某一点坐标,计算较为繁琐,实际运算中很少这样算.在解决极点极线背景的问题时,常常需要由一个点的坐标求出另一个点的坐标,然后再进行下一步的计算,因此我们大可放下设线联立的套路,采用设点法来进行运算.在教学实践中,如果面对的是抛物线中的问题,由于抛物线方程简单,引入参数描述抛物线上的点,用设点法来解决问题经常是师生的首选.椭圆、双曲线标准方程比抛物线标准方程复杂一点,所以容易形成一个错误认知,椭圆、双曲线的问题设点法计算困难,只能选择设线法来解.其实设点与设线,只是思考问题时出发点不一致,从原理上讲,能用设线策略解决的问题,设点策略也可以解决.在极点极线背景的试题中,以下两种情形如果用设点策略,运算效率比设线法要高出不少:


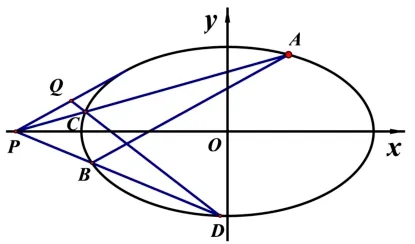
图7

图8

三、向量策略
极点极线涉及的是图形的射影性质.在中学范围内,射影性质往往表现为点在直线上、直线过定点这类与结合性相关的性质,因此极点极线背景的试题,经常要根据点共线的条件求点的坐标.处理共线问题,向量是一个有效的工具,因此向量策略在极点极线问题的求解中也是常用策略.使用向量处理点共线问题时,常会用到以下与共线有关的结论:
A、B、C三点共线⇔存在三点共线⇔存在其中O是平面内任意一点.
例6(2015年高考北京卷文科第20 题)已知椭圆x2+ 3y2= 3,过点D(1,0)且不过点E(2,1)的直线与椭圆C交于A、B两点,直线AE与直线x=3 交于点M.
(1)求椭圆C的离心率;
(2)若直线AB垂直于x轴,求直线BM的斜率;
(3)试判断直线BM与直线DE的位置关系,并说明理由.
分析观察图形易得直线BM与直线DE平行,于是考虑证明,因此可以选择向量法完成证明.
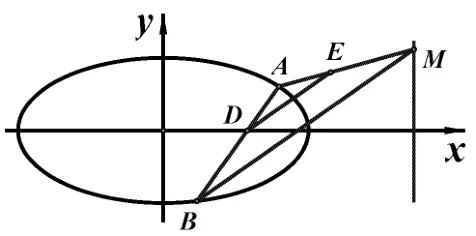
图9
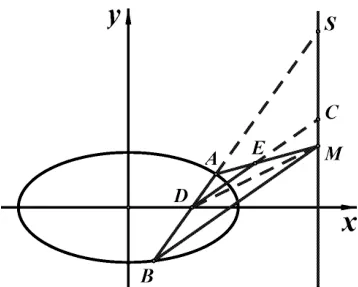
图10
四、几何策略
解析几何问题终究是几何问题,因此利用几何知识探究图形性质,配合解析法解决问题是解析几何中非常自然的策略,处理极点极线背景的问题亦是如此.
例7如图11所示,已知椭圆E:过点P(2,1)的直线交椭圆于M、N两点,过N作斜率为的直线交椭圆于另一点Q,求证:直线MQ过定点.共点,因此MQ过GP与P∞B的交点A.理清例7 背景,就不难作出例7 辅助线,减少运算量.如果没有这些辅助线,一味硬算,计算量会非常巨大.
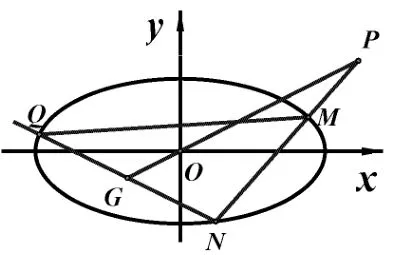
图11
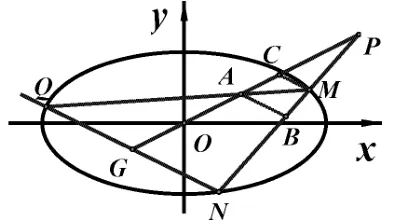
图12

五、曲线系策略
因为平面上五个点(其中无三点共线)唯一确定一条非退化二次曲线,所以二次曲线上如果有三个或者四个不共线的点,我们就可以引入二次曲线系方程来表示这条二次曲线,再比较方程的系数得到参数间的关系,这就是所谓曲线系策略.曲线系策略是解决极点极线问题的一种非常有效的策略.
例8已知椭圆E:A,B分别为椭圆E的上顶点和右顶点,与AB平行的直线MN与椭圆E相交于M、N两点,记k1,k2分别为AM与BN的斜率,求证:k1k2为定值.
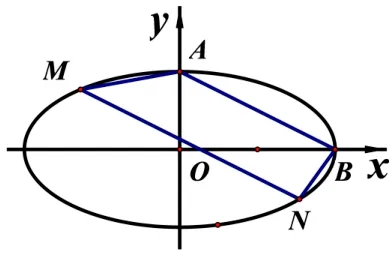
图13
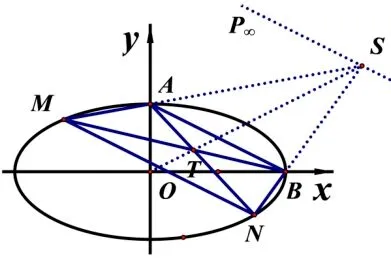
图14

