由2019年高考北京卷第17题引发的联想

北京市房山区教师进修学校(102401)刘雪明

1 试题再现

题目(2019年高考北京卷理科第17 题节选)改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100 人,发现样本中A,B两种支付方式都不使用的有5 人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:

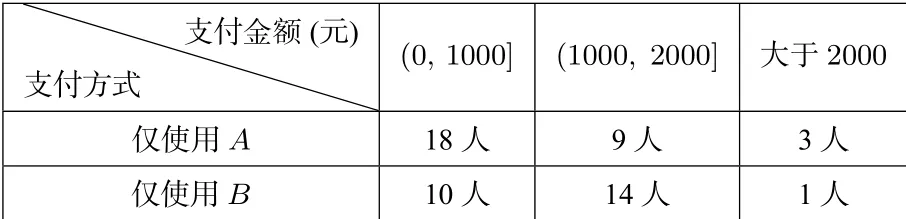
支付方式支付金额(元)(0, 1000](1000, 2000]大于2000仅使用A 18 人9 人3 人仅使用B 10 人14 人1 人

(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3 人,发现他们本月的支付金额都大于2000 元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000 元的人数有变化?说明理由.

2 试题解答

分析本题答案开放,可以有不同的结论,只要理由合理就可以.

设事件H=“从样本仅使用A的学生中,随机抽查3 人,他们本月的支付金额都大于2000 元”.

答案一认为样本仅使用A的学生中本月支付金额大于2000 元的人数有变化.

因为P(H)很小,概率很小的事件在一次试验中一般不容易发生,现在发生了,所以可以认为仅使用A的学生中本月支付金额大于2000 元的人数发生了变化.

答案二不能确定样本仅使用A的学生中本月支付金额大于2000 元的人数是否发生了变化.

虽然P(H)很小,概率很小的事件在一次试验中一般不容易发生,但是也是有可能发生的,所以不能确定仅使用A的学生中本月支付金额大于2000 元的人数是否发生了变化.

3 试题解法再分析

我们重点分析一下答案一的思维过程:

首先提出假设:假设仅使用A的学生中本月支付金额大于2000 元的人数没有变化;然后在该假设下,计算随机事件H的概率;最后进行推断:推断的依据是小概率原理(概率很小的事件在一次试验中一般不容易发生).

实际上,这就是典型的假设检验的思维过程.假设检验,是用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法.其基本原理是先对总体的特征做出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受做出推断.常用的假设检验方法有Z检验、t检验、卡方(独立性)检验、F检验等[1].

独立性检验是由被称为数理统计学之父的卡尔·皮尔逊于1900年提出的.高中阶段学习的独立性检验是一种利用χ2的取值推断某两个分类变量是否独立的统计方法,独立性检验在生物统计、医学统计、社会统计等领域有非常广泛的应用.

4 对独立性检验的再认识

独立性检验开启了人类认识世界的一种新的思维方式.学习独立性检验不仅要学会用已知的样本数据和确定的检验方法,会使用相关软件,会正确解释结果,更重要的是要理解独立性检验中蕴涵的基本思想和方法.

4.1 关于变量

有些同学可能会有疑问:相关系数可以反映两个变量之间的相关程度,为什么还要通过独立性检验来检验两个变量之间是否关联呢? 这是因为相关分析和独立性检验所研究的变量不一样.相关分析所研究的对象是数值变量,比如人的身高、数学成绩等,数值变量的取值是实数,其大小和运算都有实际意义.而独立性检验研究的对象是分类变量,分类变量是说明事物类别的一个名称,其取值是分类数据,比如“性别”是一个分类变量,其变量值为“男”或“女”,“学业成绩”也是一个分类变量,其变量值为“优秀”、“合格”、“不合格”.分类变量值也可以用实数表示,比如男生、女生可以用1,0表示,优秀、合格、不合格可以用1,2,3 表示,这些实数一般只作为标记使用,并没有通常的大小和运算意义.高中阶段的独立性检验中涉及的分类变量均有两个变量值.

4.2 关于假设

有些同学可能还会有疑问:为什么要先提出假设? 零假设能设为两个分类变量相关吗? 实际上,假设在实际生活中无处不在,只是我们没有意识到而已.当我们要对一件事物做出判断的时候,其中就隐含着假设.假设检验要求把这个隐含的假设显性化,也是为了首先明确检验的目的.假设包含原假设(记作H0)和备择假设(记作H1),原假设也叫零假设,备择假设也叫对立假设,原假设和备择假设是相互对立的.“是不是互为对立的两个假设中哪一个作为零假设都可以呢? ”回答是否定的,假设的设置遵循着一些原则:

(1)保护原假设.如果错误地拒绝假设A比错误地拒绝假设B带来更严重的后果,则选A作为原假设;比如在检验“某药物是否有毒副作用”时,一般H0为“药物有毒副作用”.

(2)原假设维持现状.为解释某些现象或效果的存在性,原假设常取为“无效果”“无改进”“无差别”等,拒绝原假设表示有较强的理由支持备择假设.比如在前面高考题中,H0为“人数没有变化”.在独立性检验中,一般H0为“两个变量不相关”.可见,原假设和备择假设的地位是不对等的.

在这些原则的基础上,广大师生在教学实践中也总结出一些简单易行的确定假设的方法:一般把有历史数据或经验支持的陈述作为原假设,把需要充分理由支持的陈述作为备择假设.

4.3 关于构造χ2 统计量的基本思路

关于χ2的构造过程,我们只要理解其合理性就可以了.χ2值表示观察值与期望值之间的差异,χ2的构造思路:

(1)设A代表观察频数,E代表基于H0计算出来的期望频数,A与E之差称为残差;教材中通过实例解释了观察频数与期望频数的含义[2];

(2)仿照方差的构造过程,不能将所有残差简单相加,可以将残差平方后相加;

(3)残差大小是相对的,比如,相对于期望频数10,残差50 就很大,但相对于期望频数1000,残差50 就非常小.为了合理平衡这种影响,又将残差平方除以期望频数后再求和.于是得到χ2统计量,.

可以算出,在2×2 列联表中,

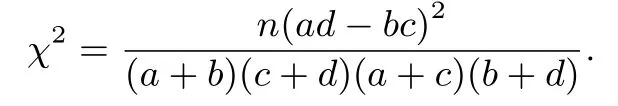
4.4 关于临界值

正态分布是一个连续型随机变量的分布,我们知道,若X ～N(μ,σ2),则X取值不小于x的概率P(X≥x)为图1中区域A的面积,x值越大,区域A的面积越小,也就是相应的概率值越小;概率值越小,x值越大.对于任何小概率值α,可以找到相应的实数xα,使得P(X≥xα)=α,称xα为α的临界值.

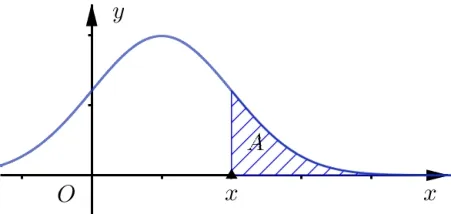
图1

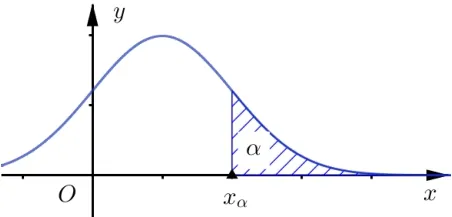
图2

统计上已经证明，在假定H0的条件下,当样本量很大时,χ2近似服从一个已知的分布χ2(1),并可以得到几个常用的小概率值和相应的临界值.我们可以类比正态分布来理解独立性检验中的临界值.表1 给出了独立性检验中几个常用的小概率值和相应的临界值

表1

由表1 可知,P(χ2≥ 3.841)≈0.05.可理解为在H0成立的情况下,χ2的观测值大于等于3.841 的概率不会超过0.05.现在在一个具体问题中由抽样数据算得χ2= 5.059＞3.841,这表明这一事件发生的概率不会超过0.05,这是一个小概率事件,但是发生了.因此,可以认为H0不成立,从而判断X与Y有关系.我们做出这样的判断有可能犯错误,χ2的观测值仍然可能大于3.841,但这一事件发生的概率不超过0.05,也就是说犯错误的概率不超过0.05.

4.5 独立性检验的一般步骤

设两个分类变量X,Y均有两个变量值,独立性检验的一般步骤:

(1)提出原假设H0:X与Y相互独立;

(2)根据2×2 列联表,计算χ2的值;

(3)确定临界值xα,得出推断结论:

若χ2＞xα,拒绝H0,认为“X与Y之间有关系”,此时犯错的概率不超过α;

若χ2＜xα,就认为没有充分的证据拒绝H0,于是接受H0,认为“X与Y相互独立”.

4.6 反证法与独立性检验

用反证法证明结论A正确的一般步骤是:首先否定A,即假设结论A错误,然后以结论A错误为前提条件进行推理,推理得出一个矛盾结论,从而说明假设不成立,即结论A正确.在全部逻辑推理正确的情况下,反证法不会犯错.

独立性检验的统计思想是:要研究“两个分类变量有关系”的可靠程度,首先假设该结论不成立,即假设“H0:两个分类变量没有关系”成立[3],在该假设下,如果出现一个与H0相矛盾的小概率事件,则推断H0不成立,且该推断犯错误的概率不大于这个小概率值.从反证法与独立性检验的比较中我们还可以再次感受到,原假设与备择假设的不对等性.

身处大数据时代,统计无处不在,数据分析素养已成为当代公民必备素养之一.我们学习常用统计方法,就要领悟其思想、从数据中找出规律、感悟推断结果的合理性,并运用统计知识解决实际问题,进一步体会统计的作用与价值.