基于区间q-Rung Orthopair模糊正弦相似测度的决策方法
2022-03-24林志超周礼刚陆艾静陈婷婷
徐 露,林志超,周礼刚,陆艾静,陈婷婷
(安徽大学 数学科学学院,安徽 合肥 230601)
多属性决策在人们实际生活中起着十分重要的作用,是指决策者对不同方案的属性做出相应的评价值,通过对多个属性的评估,最终选择一个最优方案的过程。目前,多属性决策在金融风险管理、人工智能、医药评估等领域应用广泛。但在实际决策中,由于环境的复杂性和人类认知的局限性,决策者难以用一个单独且准确的评价数字来量化信息。因此,ZADEH[1]给出了模糊集的概念,奠定了模糊集相关理论的基础,用隶属度来描述对象的模糊性。随后,为了扩展模糊集,ATANASSOV[2]将模糊集推广到直觉模糊集,用隶属度和非隶属度来刻画对象,但两者之和不能大于1。为了更精确地描述对象的模糊性,YAGER[3]拓宽了直觉模糊集的范围,毕达哥拉斯模糊集理论进而产生。YAGER[4]进一步提出了q-Rung Orthopair模糊集的概念,其中隶属度与非隶属度的q次方之和不超过1。此时的隶属度和非隶属度均是用[0,1]的实数来表示。但是随着社会环境的多元化发展,单个实数难以表达全面客观的评价信息,于是WANG等[5]提出了区间q-Rung Orthopair模糊集的理论,用隶属度和非隶属度区间来代替之前的[0,1]上的实数。由于q-Rung Orthopair模糊集的适用性和广泛性,许多学者对此展开了讨论研究。RANI等[6]提出了一种新的q-Rung Orthopair模糊集相似度度量方法和广义改进分数函数,在此基础上发展了标准权重评估方法;LIU等[7]提出了加权广义麦克劳林对称均值(q-ROFWGMSM)和加权广义几何麦克劳林对称均值(q-ROFWGGMSM)算子;LI等[8]采用基于区间q-Rung Orthopair模糊集的加权几何聚合算子来处理复杂的偏好信息,并应用到决策选择排序中。
TOPSIS方法是一种多属性决策方法,其基本思想是通过比较可行方案与正负理想解的接近程度来选择最优方案。随着决策问题的复杂性和模糊性越来越高,一些学者将TOPSIS方法拓展应用到模糊环境中,如SUN等[9]定义了相似正负相关系数决策因子和距离类正负相关系数决策因子,构建了一种新的TOPSIS方法,并提出犹豫模糊多属性决策方法;WANG等[10]在q-Rung Orthopair犹豫模糊环境中提出了一种改进的TOPSIS模型。值得注意的是,相似性测度常被用来衡量模糊集间的相似程度,多被用到模式识别、决策分析等模糊环境中。如XU等[11]定义了区间q-Rung Orthopair模糊集的一些距离和相似测度;杨勇等[12]通过考虑隶属度、非隶属度和犹豫度3方面的信息,定义了一种关于直觉模糊集的正弦相似测度。
基于上述理论,笔者提出一种新的区间q-Rung Orthopair正弦相似测度,并研究该测度的优良性质,同时考虑到决策者权重和属性权重未知的情形,利用权重优化模型求解出决策者最优权重和属性最优权重,进而提出一种基于该相似测度的TOPSIS多属性决策方法,并通过实例说明其合理性和可行性。
1 预备知识
定义1设X为一论域,则称I={
定义2设X为一论域,则称P={

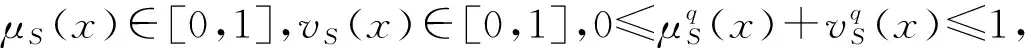
可以看出,当q=1时,S是X上的一个直觉模糊集;当q=2时,S是X上的一个毕达哥拉斯模糊集,q-Rung Orthopair模糊集是对直觉模糊集和毕达哥拉斯模糊集的推广。

显然,区间q-Rung Orthopair模糊集是q-Rung Orthopair模糊集的推广形式。

(1)
(2)

2 一种新的区间q-Rung Orthopair模糊相似测度

(3)








3 基于新的区间q-Rung Orthopair正弦相似测度的多属性决策方法


(4)

(5)

(6)
(7)
(8)
(5)根据式(9)和式(10)分别计算各个方案Ai与正理想解、负理想解的相似度:
(9)
(10)
(6)计算各个方案Ai的贴近度σi,σi越大,说明该方案越优。
(11)
4 案例分析
随着经济全球化快速发展,各行各业针对专业人才的需求不断增加,高校人才引进对建成高水平的师资队伍,为社会源源不断地培养并输出专业人才具有重要意义。某高校要从海外5位专业人才Ai中选择一位引进到本校,并组织3位专家构成评审团队,分别为学校校长T1、管理学院院长T2和人事处处长T3,3位评审专家将从思想道德C1、科研能力C2、教学技能C3和教育背景C4这4个方面对5位海外人才进行评审,并依据候选人才提供的个人材料,使用区间q-Rung Orthopair模糊数给出相应的评价值。3位评审专家对5位海外人才的具体评价信息如表1~表3所示。

表1 专家T1的区间q-Rung Orthopair 模糊评价矩阵A(1)

表2 专家T2的区间q-Rung Orthopair 模糊评价矩阵A(2)

表3 专家T3的区间q-Rung Orthopair 模糊评价矩阵A(3)
基于3位专家的评价信息,利用所提出的基于区间q-Rung Orthopair正弦相似测度的TOPSIS多属性决策方法进行分析(这里取q=2),具体决策过程如下:


表4 区间模糊综合评价矩阵B
(3)根据优化模型(6)求解得到属性最优权重w*=(0.002 7,0.009 6,0.545 9,0.441 8)。
(4)根据式(7)和式(8)确定方案的正理想解、负理想解分别为:


(5)根据式(9)和式(10)计算方案Ai与正理想解、负理想解的相似度分别为:
S+=(0.503 3,0.992 8,0.117 9,0.626 4,0.183 2)
S-=(0.205 4,0.119 3,0.993 1,0.146 1,0.351 7)
(6)根据式(11)计算方案Ai的贴近度分别为:σ1=0.710 2,σ2=0.892 7,σ3=0.106 1,σ4=0.810 9,σ5=0.342 6,根据贴近度大小对方案进行排序,即A2≻A4≻A1≻A5≻A3,最优方案为A2,因此第二位海外人才为最优候选者。
为分析不同参数q值对方案贴近度σi的影响,分别对q取值2~8,重复上述步骤,观察各方案贴近度的变化情况,计算结果如表5所示。由表5可知,对于新的区间q-Rung Orthopair正弦相似测度,除q=6外,其他参数q值下最优候选者均为第二位或第五位候选者。这与文献[16]中态度参数γ∈[0,0.7]时,第二位为最优候选人,γ∈(0.7,1]时,第五位为最优候选人的结果几乎相同,这表明笔者所提出的方法对解决多属性群决策问题具有一定的实用性和参考价值。
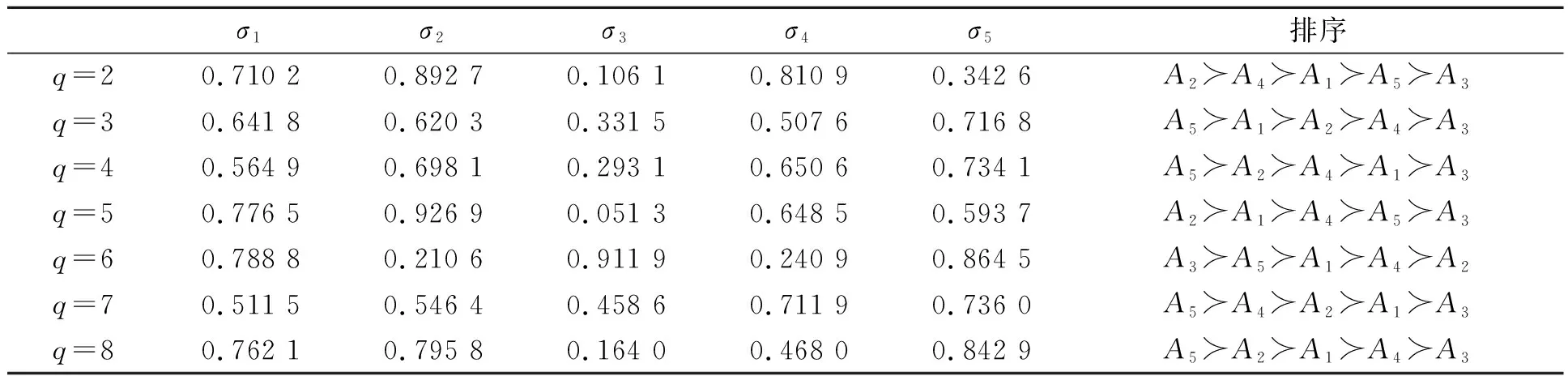
表5 不同q值下5位海外人才的贴近度σi及其排序结果
方案贴近度σi随区间q-Rung Orthopair正弦相似测度参数q值改变情况如图1所示,可以看出方案A5的贴近度随q值增大后基本处于上游区域,方案A1的贴近度从q=2开始逐渐下降后呈缓慢上升趋势,有些起伏,后期逐渐靠近方案A2,方案A2和A4的贴近度随q值变化较为同步,且相差不大,在中游位置起伏变化,方案A3的贴近度除q=6外,始终最小。各方案的贴近度均具有一定程度的起伏变化,大多数情况下方案A5和方案A2总是优于其他方案。这说明在解决实际问题时,需要根据实际情况和决策者自身偏好选择合适的参数q值。

图1 方案贴近度随区间q-Rung Orthopair正弦相似测度参数值改变情况
5 结论
(1)基于正弦函数的直觉模糊集相似测度,提出了区间q-Rung Orthopair模糊正弦相似测度,并研究了其相关性质,对直觉模糊集的相似测度的推广。
(2)对于多属性决策问题,如何确定决策者权重和属性权重是十分重要的。笔者在各决策者权重、方案属性权重均未知的情况下,分别构建决策者权重与属性权重求解模型,降低了主观性。
(3)结合TOPSIS方法,利用得分函数确定正负理想解,运用区间q-Rung Orthopair模糊正弦相似测度计算各方案与正负理想解的相似度,求解得到各方案的贴近度,由大到小进行排序择优,并最终将其应用到人才引进决策过程中,证明了该方法的有效性和可行性。
