基于模糊影响图的冬奥全球赛事突发危机事件风险评估
2022-03-24周义棋杨宇轩钟茂华
苏 鑫,周义棋,杨宇轩,钟茂华
(清华大学 公共安全研究院,北京 100084)
北京2022年冬奥会是国际重大标志性活动,是展现我国国家形象、促进国家发展、振奋民族精神的重要契机。新冠肺炎疫情在世界各地持续蔓延,许多大型体育赛事被迫推迟或取消。习近平总书记在冬奥会筹办工作汇报会上强调,切实把筹办工作重点放在统筹抓好疫情防控和组织好赛事上来。围绕如期办赛目标,突出“简约、安全、精彩”办赛新要求,全面防范化解各种风险,最大限度降低疫情风险。冬季是传染病疫情、寒潮、风雪等灾害的高发期,突发危机事件风险评估工作是科学高效处置冬奥赛事突发危机事件的基础支撑,更是我国安全举办冬奥会、塑造国家形象、构建人类命运共同体的核心任务。因此,分析北京冬奥会背景下突发危机事件的风险因素及因素间相互作用与影响,建立风险评估模型,预测冬奥赛事突发危机事件的风险概率,并采取干预措施,对保障北京冬奥会安全办赛、提升国家形象具有重要意义。
2008年成功举办北京奥运会以来,体育赛事风险评估与防控受到了学术界的高度关注。随着理论探讨的进一步深入,各种定性和定量研究方法在体育赛事风险评估方面得到广泛应用。关于大型体育赛事风险评估的研究方法主要分为3个方面:①风险致因性评估,采用文献分析、情景推演、损失清单排列等方法,分析大型体育赛事面临的网络安全风险、赛事运行规律等,构建不同层次的风险评估体系并进行权重分析,提出预防措施及管理建议[1-2];②严重程度分析,采用仿真方法模拟计算事故过程,确定风险范围后评估损失[3];③风险预警分析,构建风险预警指标体系,根据赛事风险特征、突发危机事件风险因子、事故风险抵消因子等对体育赛事风险进行评估,采用神经网络分类、模糊层次分析、德尔菲、帕累托分析等方法对因子风险程度进行分类及风险等级划分[4-5]。此外,还有学者采用结构方程模型对体育赛事风险进行质证分析[6]。但以上研究方法需要一定的适用条件,且忽略了影响因素之间的关系,具有主观性强或决策现实考虑不全等缺点。
鉴于此,笔者采用模糊影响图方法,从风险评估目标入手,逐级递进式识别风险的各类节点(包括价值、机会、独立、中间节点),建立风险影响因素模糊不确定性的数值层,通过函数层的计算明确节点间关系,最后计算价值节点的频率矩阵确定隶属度并计算概率分布,求得冬奥全球赛事突发危机事件发生风险的概率,并通过模糊关系明确风险因素关系链。模糊影响图方法直观且灵活,是很好的决策建模工具[7],有助于决策者有效解决动态环境下的复杂、非线性决策问题,构造决策问题的影响结构并揭示变量间的关系,且能够基于不确定推理得到答案[8]。
1 风险评估方法
1.1 模糊影响图
基于图论视角,直接图是由一组特定的节点和直弧组合成的图形,网络则是在节点与弧中包含条件数据的图形。因此,影响图应该是一个由非循环直接图构成的网络。具体来说,包括3个层次:①关系层,对问题进行定性分析,是关系层次的诠释,确定风险评估的整体结构,关系层的构造过程包括价值节点确定、机会节点识别、节点核查合并、节点编码实现;②数值层,单一节点的模糊不确定性是通过数值层来描述的,数值层包含状态模糊集和频率模糊集两个集合;③函数层,明确节点间变量间的关系。影响图类似于决策网络,可以处理诸如概率评估、推理识别、预测研判等复杂决策问题。需要注意的是,影响图一般对边缘概率与条件概率的准确性要求很高,其准确性直接影响研究对象的评价效果,而冬奥全球赛事突发危机事件处于快速变化的复杂环境之中,再加上人们认知的偏差,较难准确地评估出相应的概率值,模糊集理论为解决概率评估问题提供了很好的思路[9]。因此,将模糊数学与影像图相结合的模糊影响图方法,为冬奥全球赛事突发危机事件风险评估提供了很好的评价建模与计算工具。
1.2 评估算法
在SHACHTER[10-11]研究的基础上,结合相关文献对模糊影响图算法进行设计,包括节点模糊关系[12]、独立节点评估算法[13]、非独立节点评估算法和价值节点概率分布[14]。
1.2.1 节点模糊关系
假设V=(G,α)为数据图,G=(Am,E)为一个无循环直接图;Am={x1,x2,…,xm}为节点随机变量;α:Am={1,2,…,m}为与G对应的节点序号;对于弧(xi,xj)∈E,α(xi)<α(xj)。Am={x1,x2,…,xm}的紧前影响图是Am基于m-1个条件独立的(G,α),即xr⊥{xj|α(xj)<α(xr)}|P(xr),α(xr)=2,3,…,m。其中,P(xr)⊆{xj|α(xj)<|α(xr)},xi∈p(xr)⟺(xi,xr)∈E;若Q(xj)为节点xj的集合,在Am中没有从xi到xj的直接图,则xi⊥Q(xj)|P(xi),P(xi)为xi的直接前序节点。
影响图求解的难点是构建各个节点的边缘概率及不同节点之间的条件概率。一般来说,概率分布是依据从前的经验进行推断的,亦或是基于知识认知主观判断出来的,边缘概率和条件概率的估计可能会存在很大误差。另外,主观概率估计方法还可能会出现违反概率理论的情况。模糊影响图将影响图方法与模糊集理论相结合,允许模糊集间的交叉重叠,可以克服上述困难。
假设模糊集合中两个模糊子集A和B之间的模糊关系为R,而μR(xi,yj)=μA×B(xi,yj)=min[μA(xi),μB(yj)]。其中,x∈U,y∈V,U、V分别为论域。两个模糊关系R与S的和为R∪S,其特征值为μR∪S(xi,yj)=max[μR(xi,yj),μS(xi,yj)],R与S的交R∩S的特征值为μR∩S(xi,yj)=min[μR(xi,yj),μS(xi,yj)]。
1.2.2 独立节点评估算法
语言变量的量化是基于模糊集理论解释影响图中节点之间关系的基础。因此,要对两个类型的模糊集进行定义。其中一种是描述独立节点的事件和发生频率;另一种是表示前序和后序节点之间的模糊关系。影响关系示意图如图1所示,X为明确频率矩阵的独立节点(即无紧前节点),X的向量可表示为PX=(PX1,PX2,…,PXn)T,PX1,PX2,…,PXn为基于语言变量定义得到的事件模糊集合。假设独立节点X的频率向量为fX=(fX1,fX2,…,fXn)T,fX1,fX2,…,fXn是与节点X的频率向量中的每个可能状态相对应的频率模糊集合,则独立节点X的频率矩阵FX可表示为:
FX=(fX1×PX1)∪(fX2×PX2)∪…∪(fXn×PXn)
(1)

图1 影响关系示意图
1.2.3 非独立节点评估算法
参照文献[14]的研究设计非独立节点评估算法。由图1可知,如果节点Z的前一个节点是m个随机节点Y1,Y2,…,Ym,则Z的所有前序节点频率矩阵的联合FZP为:
FZP=FY1∪FY2∪…∪FYm
(2)
从节点Y1到节点Z的模糊关系RY1Z为:
RY1Z=(PY11×PZi)∪(PY12×PZi)∪
…∪(PY1n×PZi)
(3)
式中:PY11,PY12,…,PY1n∈PY1;PZi∈{PZ1,PZ2,…PZn}=PZ。
从节点Ym到节点Z的模糊关系RYmZ为:
RYmZ=(PYm1×PZi)∪(PYm2×PZi)∪
…∪(PYmn×PZi)
(4)
则模糊关系RY1Z,RY2Z,…,RYmZ的联合为:
RZP=RY1Z∪RY2Z∪…∪RYmZ
(5)
节点Z的频率矩阵FZ为:
FZ=FZP∘RZP
(6)
1.2.4 价值节点概率分布
从价值节点频率矩阵FZ中,选择使该行之和与其相对应的频率乘积在所有行中最大的行作为随机结果的隶属度,因此每个随机结果的概率函数可表示为:
(7)
2 突发危机事件风险分析过程
2.1 节点识别
2.1.1 价值节点与机会节点
对冬奥赛事突发危机事件进行风险评估,分析各风险因素的作用力大小及因素间相互作用关系,因此选取冬奥赛事突发危机事件风险水平作为价值节点。
冬奥赛事突发危机事件的风险因素多样且复杂,为了尽量简化并能有效识别各类风险,从宏观角度考虑突发危机事件的引发因素、属性类别及发生机理,将突发危机事件划分为4类,即自然灾害、事故灾害、公共卫生事件和社会安全事件。同时,根据近一年来对全球知名智库、学者、杂志及媒体文献的数据监测,可知北京冬奥会已经成为国际社会重点关注的议题之一。鉴于涉北京冬奥会国际舆情特征与趋势,考虑北京冬奥会在国际上的影响力,将冬奥赛事突发危机事件的影响因素划分为5个方面,分别为自然灾害、事故灾害、公共卫生事件、社会安全事件和舆情意识形态。
2.1.2 独立节点与中间节点
2022北京冬奥组委发布的《防疫手册》指出,将实施全点位全过程闭环管理。综合考虑冬奥会的管控措施与冬奥会的风险特征,按照节点选取的全面性、科学性、系统性原则,对风险指标进行精减与逻辑关联构建。自然灾害的子节点选取气象灾害、地震灾害、地质灾害、水旱灾害、森林草原火灾、海洋灾害和生物灾害7个节点;事故灾害子节点选取环境污染事件、生态破坏事件、公共设施与设备事故、交通运输事故、企业各类安全事故、重大群体性事件6个节点;公共卫生事件子节点选取传染病疫情、群体性不明原因疾病、动物疫情、食品安全、职业危害、其他严重影响生命健康与公共安全的事件6个节点;社会安全事件子节点选取生产安全事件、经济安全事件、交通安全事件、生活安全事件、社会治安事件5个节点;舆情意识形态子节点选取法规因素、政治因素、社会因素、文化因素、专业因素和传播技术因素6个节点。
2.2 拓扑层构建
对风险指标进行精减与逻辑关联构建后画出影响图,并对风险影响节点进行编码。冬奥赛事突发危机事件风险水平的模糊影响图拓扑结构如图2所示,其中1~36为节点序号。
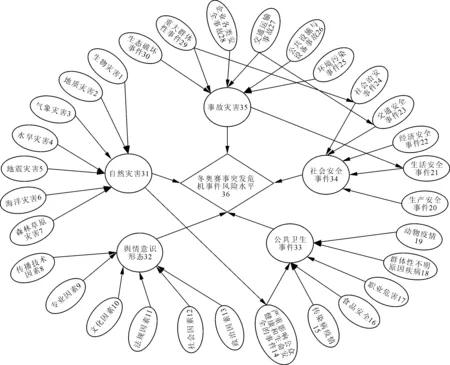
图2 突发危机事件风险水平的影响拓扑结构
2.3 突发危机事件风险关系构建
2.3.1 频率模糊集
定义概率论域U={0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0},划分频率范围。确定频率模糊集及隶属度:高(h)={0.7|0.5,0.8|0.7,0.9|0.9,1.0|1.0};中(m)={0.3|0.2,0.4|0.8,0.5|1.0,0.6|0.8,0.7|0.2};低(l)={0.0|1.0,0.1|0.9,0.2|0.7,0.3|0.5};非常高(vh)=(h2)={0.7|0.25,0.8|0.49,0.9|0.81,1.0|1.0};非常低(vl)=(l2)={0.0|1.0,0.1|0.81,0.2|0.49,0.3|0.25}。
2.3.2 状态模糊集
描述不确定性的状态模糊集及隶属度:增加很少(NA)={1.0|0%,0.8|10%};增加较少(LA)={0.5|10%,1.0|20%,0.7|30%};增加较多(MA)={0.4|30%,1.0|40%,0.8|50%,0.2|60%};增加很多(HA)={0.8|60%,1|70%,0.9|80%};增加非常多(GA)={0.4|80%,0.8|90%,1.0|100%}。
部分独立节点状态为确定性取值,按照以下方法确定其状态模糊集及隶属度:严重(G)={严重|1.0,中等|0.4,轻微|0.0};中等(M)={严重|0.4,中等|1.0,轻微|0.4};轻微(T)={严重|0.0,中等|0.4,轻微|1.0}。
2.3.3 建立数值层与函数层
按照紧前节点模糊计算传递至紧后节点,计算紧后节点的模糊频率。因此,对独立节点进行模糊估计,求其频率模糊集合和状态模糊集合,并基于层级关系计算得到价值节点的频率矩阵。选取危机事件风险评估相关领域的15位专家,利用专家的经验、知识与技能,采用专家判断法,依据冬奥会举办期间的气候特征、举办赛区以往的公共安全事件与事故灾害发生特征及对疫情趋势研判结果,结合态势感知获取冬奥赛事相关舆情信息,分析独立节点间的模糊关系,确定独立节点频率估计及其紧前节点、紧后节点关系,如表1所示。
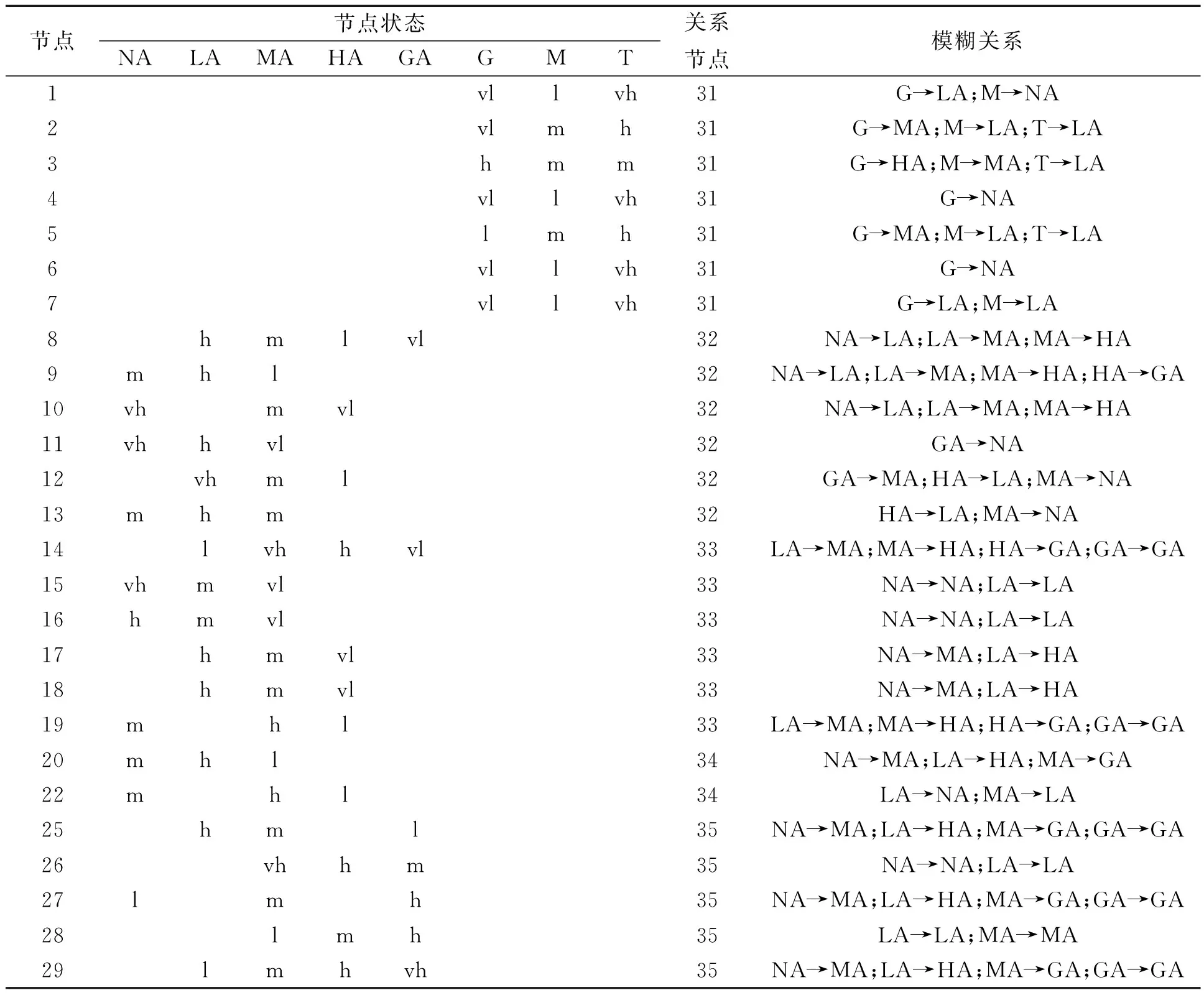
表1 各个节点频率和不同节点模糊关系
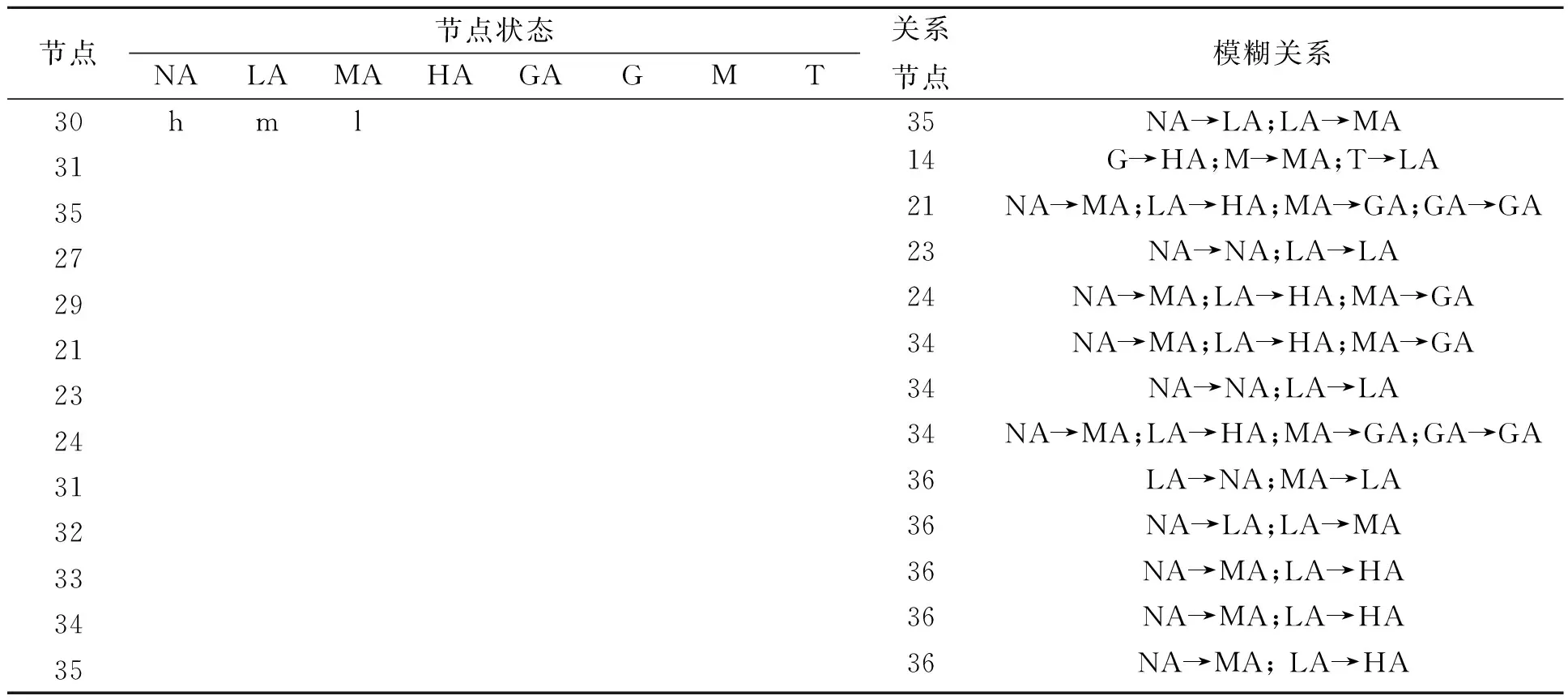
续表1
2.3.4 独立节点频率矩阵
由式(1)可得独立节点频率矩阵并逐步释放各个节点,F(1)~F(20)、F(22)、F(25)~F(30)的频率矩阵为:

2.3.5 非独立节点频率矩阵
(1)非独立节点的紧前节点频率矩阵联合。先计算所有前一个节点的频率矩阵的联合及与所有前一个节点的模糊关系:F(14A)=F(31A);F(21A)=F(35A);F(31A)=F(1)∪F(2)∪F(3)∪F(4)∪F(5)∪F(6)∪F(7);F(32A)=F(8)∪F(9)∪F(10)∪F(11)∪F(12)∪F(13);F(23A)=F(27);F(24A)=F(29);F(33A)=F(14)∪F(15)∪F(16)∪F(17)∪F(18)∪F(19);F(34A)=F(20)∪F(21)∪F(22)∪F(23)∪F(24);F(35A)=F(25)∪F(26)∪F(27)∪F(28)∪F(29)∪F(30);F(36A)=F(31)∪F(32)∪F(33)∪F(34)∪F(35)。再由式(2)可得节点F14、F21、F23、F24、F31~F36的紧节点频率矩阵联合:

(2)模糊关系矩阵联合。依据表中的结点关系,由式(5)可得节点间的模糊对应关系:R(14P)=R(31-14);R(21P)=R(35-21);R(19P)=R(10-19)∪R(11-19);R(24P)=R(29-24);R(31P)=R(1-31)∪R(2-31)∪R(3-31)∪R(4-31)∪R(5-31)∪R(6-31)∪R(7-31);R(32P)=R(8-32)∪R(9-32)∪R(10-32)∪R(11-32)∪R(12-32)∪R(13-321);R(33P)=R(14-33)∪R(15-33)∪R(16-33)∪R(17-33)∪R(18-33);R(34P)=R(20-34)∪R(21-34)∪R(22-34)∪R(23-34)∪R(24-34);R(35P)=R(25-35)∪R(26-35)∪R(27-35)∪R(28-35)∪R(29-35)∪R(30-35);R(36P)=R(31-36)∪R(32-36)∪R(33-36)∪R(34-36)∪R(35-36)。进而得到所有紧前节点模型关系矩阵联合:

(3)含紧前节点的频率矩阵。基于式(6)可知,F(14)=F(14P)∘R(14P);F(21)=F(21P)∘R(21P);F(23)=F(23P)∘R(23P);F(24)=F(24P)∘R(24P);F(31)=F(31P)∘R(31P);F(32)=F(32P)∘R(32P);F(33)=F(33P)∘R(33P);F(34)=F(34P)∘R(34P);F(35)=F(35P)∘R(35P),则含紧前节点的频率矩阵为:

2.3.6 价值节点频率矩阵
得到节点14、21、23、24、31~36的频率矩阵后,说明节点已被释放,最后需计算价值节点36的频率矩阵。先计算其所有紧前节点频率矩阵联合与所有紧前节点模糊关系联合,再由F(36)=F(36A)∘R(36P)可得冬奥全球赛事突发危机事件风险节点的频率矩阵F(36):
通过价值节点36的频率矩阵可确定节点36的变动概率分布。由式(7)确定隶属度,从矩阵F(36)中选择所有行中该行与其对应频率之和的乘积最大的行,并计算概率分布和概率累计情况,如表2所示。

表2 价值节点概率分布
由表2可知,冬奥全球赛事突发危机事件风险在10%~30%的累计概率为0.212 5,30%~60%的风险累计概率为0.325 0,60%~80%的风险累计概率为0.237 5。由此分析,冬奥全球赛事突发危机事件风险属于中等偏高风险。根据对冬奥全球赛事突发危机事件风险概率的分析结果,明确突发危机事件属于30%~60%间的累计概率最大,依据隶属度与模糊状态间的关系,按照表1中的关系进行推导,突发危机事件风险主要影响过程如图3所示。
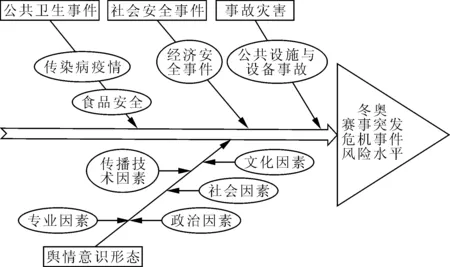
图3 冬奥全球赛事突发危机事件风险较高的关键节点
由图3可知,冬奥全球赛事突发危机处于中等偏高风险的原因主要受到事故灾害、社会安全事件、公共卫生事件及舆情意识形态的作用,其中公共设施与设备事故增加了事故灾害的风险;针对冬奥赛事的社会安全事件受到经济安全的影响;食品安全与传染病疫情使公共卫生事件发生的风险增加;影响舆情意识形态的风险关键节点较多,包括文化因素、社会因素、政治因素、传播技术因素和专业因素。
3 结论
(1)基于冬奥全球赛事突发危机事件风险问题,以风险评估为目标,针对冬奥全球赛事重点区域防控需求,分析冬奥赛事突发危机事件的风险因素,依据突发危机事件基本属性和常用类型划分标准,从自然灾害、事故灾害、公共卫生事件、社会安全事件和意识形态5个方面确立了36个风险评估指标。
(2)通过模糊影响图风险评估方法定义突发危机事件风险的频率模糊集与状态模糊集,并建立数值层与函数层以较好地表征冬奥全球赛事突发危机事件过程节点的风险水平,在风险分析结果中可更加直观地观察到冬奥全球赛事突发危机事件风险属于中等偏高风险。
(3)通过模糊关系推理,确定冬奥全球赛事突发危机事件风险的关键节点,包括事故灾害中的“公共设施与设备事故”;社会安全中的“经济安全事件”;公共卫生中的“传染病疫情”“食品安全”;舆情意识形态中的“文化因素”“社会因素”“政治因素”“传播技术因素”“专业因素”。关键节点的确定将有助于采取更有针对性的风险防控措施。
(4)笔者研究在一定意义上揭示了冬奥全球赛事面临的突发危机事件风险,为风险防控的关键领域与重点方向提供了一定的参考。结合研究结论,针对冬奥全球赛事突发危机事件风险防控提出以下几点建议:①在应对国际舆情事件方面,要防范外部势力的干扰抵制,谨防境外各类反华势力将北京冬奥会政治化,做好应急处置和舆论防控,引导舆论良性发展;②在应对事故灾害事件方面,要提高应对突发事件和潜在风险的能力,完善冬奥场馆等的配套设施建设,强化极端天气预警;③在应对公共卫生事件方面,要全面落实闭环管理措施,做好冬奥防疫与城市防疫无缝对接,内外联动保障赛事与城市双安全,严格遵循《防疫手册》,坚持常态化防疫。
