基于犹豫度特征改进的新的直觉模糊相似度

韩 琦，李为民，罗 骁

（1.空军工程大学防空反导学院，西安 710051；2.国防大学联合作战学院，石家庄 050000）

0 引言

直觉模糊集（Intuitionistic Fuzzy Sets，IFSs）最初由著名学者K.Atanassov［1］于1986 年提出。作为近年来新兴的研究领域，其理论和应用研究受到国内外众多学者的关注，成为当前研究的一个热点领域，发展很快，是Zadeh 模糊集理论最有影响力的一种扩展和发展。

直觉模糊集相似度，直觉模糊距离，直觉模糊熵等作为直觉模糊集之间的度量方式，是直觉模糊聚类分析，直觉模糊推理与应用，直觉模糊多属性决策等应用的基础。Chen［2］，Eulalia Szmidt［3］等提出了直觉模糊集间的相似度距离在直觉模糊集之间的度量及应用；Hung［4］等研究了基于Hausdorff 距离的直觉模糊相似度；Zeshui Xu［5］研究了直觉模糊相似度及在多属性决策上的应用。除了以上研究，现存方法还有很多，它们各有侧重点，且满足绝大部分直觉模糊相似度的条件，但这些方法几乎都会在某些应用情况下出现反例。

本文针对直觉模糊集产生信息的“波动性”和“不确定性”特点，对直觉模糊相似度进行了补充拓展定义，并基于此给出了直觉模糊相似度的计算公式。给出的计算方法克服了现存方法存在的典型反例，从而验证了本文方法的可靠性和有效性。

1 预备知识

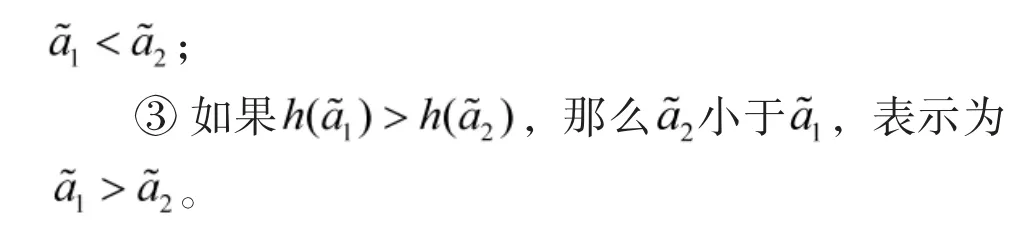
2 以往直觉模糊相似度存在的局限

3 一种新的直觉模糊相似度计算公式

文献［14］总结了以往文献中出现的反例，并建立了由不同单元素直觉模糊集构成的人工测试框架，用以测试直觉模糊相似性测度和距离。虽然这个集合不能覆盖所有的反例，但它们具有代表性。为了进一步说明所提直觉模糊相似度的有效性，本文利用测试框架中所有的IFSs 对本文所提方法和Hong 等所提方法进行比较。为了反映出直觉模糊集的特点，还在测试集中加入了一组新的单元素IFSs，扩展的人工框架测试集如表1 所示。

表1 测试的IFSs

从表2 中可以看出本文所提方法在测试集下的结果不存在反例。事实上目前绝大多数方法都存在反例，可能导致一些应用情况下无法有效区分直觉模糊集之间的差异。

表2 相似度之间的比较（加粗斜体为反例）

之所以直觉模糊集比传统模糊集能够更加有效地描述不确定信息，是因为其引入了直觉指数来刻画“亦此亦彼”的状态。在这个例子中，因为直觉指数自身包括不具体的信息即Atanassov 算子不确定（直觉指数支持和反对的比重不确定），所以即使直觉模糊集数值相同，实质上也无法确定直觉模糊集所表示的信息之间有没有差异（即此时它们之间的相似度也不一定为1）。本文所提计算相似度的方法正是体现了直觉模糊集的这一特点，因而才能更有效地计算直觉模糊集之间的相似度。

4 结论

针对直觉模糊集存在的信息波动性与不确定性因素，本文重新补充定义了直觉模糊相似度，并在此基础上提出了一种新的直觉模糊相似度公式，一方面尽可能避免反例出现，另一方面能够有效地体现直觉模糊集信息的波动性和“亦此亦彼”性。并在人工框架测试集中进行了验证，说明了所提方法的有效性。