含孔隙金属陶瓷功能梯度圆柱壳的模态频率研究

刘 超，刘文光

（南昌航空大学航空制造工程学院，南昌 330063）

0 引 言

功能梯度材料（Functionally Graded Materials，简称FGMs）作为一种新型复合材料，由于其物理属性沿着空间位置梯度分布，具有耐高温、高强度、低质量、有效缓解热应力集中等诸多优点[1-3]，在航空航天和机械工程等领域具有广阔的应用前景。

因为圆柱壳大量应用于客机的机身、轮船推进系统等领域，而且这些结构通常服役于复杂的多场耦合环境中，所以FGMs 圆柱壳的设计得到研究者的关注[4-5]。FGMs 作为一种先进材料，受其制造技术的限制，材料内部可能存在诸如气孔等缺陷[6-7]。气孔的存在不仅影响材料的声学特性和传热性能，而且还影响材料的力学行为。近年来，越来越多的研究者开始分析材料孔隙率对功能梯度壳力学行为的影响。利用一种新的半解析法，Li等[8]研究了任意边界条件下含孔隙FGMs壳的自由振动行为；基于正弦剪切理论和Rayleigh-Ritz 法，Wang 等[9]研究了不同孔隙分布形式下FGMs 壳的自由振动特性；基于一阶剪切变形理论和修正的偶应力理论，Ghadiri等[10]研究了热环境下含多孔FGMs壳的自由振动问题。

由于FGMs 的性质受体积分数定律的支配，调整FGMs的体积分数指数即可改变结构的力学性能和热传导性能，所以研究者通过提出不同体积分数模型来设计FGMs以满足工程结构在特定环境下的功能需求。现行研究中，基于幂律分布体积分数模型的FGMs 应用最为广泛[11]。以此为基础，研究者陆续提出了新的FGMs模型。Arshad等[12]将幂律分布体积分数模型修改为底数为e的指数函数分布模型；进一步地，Shah 等[13]把指数体积分数模型修改为广义的指数体积分数模型。但是，由于基于幂律分布或指数分布体积分数模型设计的FGMs结构可能在连续但快速变化的材料界面上出现应力集中，所以Chi 等[14]提出了一种Sigmoid 型分段体积分数模型，该模型结构可以在一定程度上降低应力集中的影响。以Sigmoid 型FGMs（S-FGM）圆柱壳为对象，Nguyen 等[15]采用三阶剪切变形理论研究了含孔隙S-FGMs圆柱壳的非线性动力响应；Wang等[16]采用伽辽金法及谐波平衡法研究了纵向运动S-FGMs板的非线性受迫振动特性。

工程实际应用中，因为FGMs圆柱壳经常与一些弹性介质接触，比如航天飞机推进剂罐、装满固体推进剂的弹道导弹外壳、地上和地下的储液罐、地下管道以及换热器/冷凝器等，在影响FGMs 圆柱壳振动特性的诸多因素中，弹性基础是其中之一。因此，有必要了解FGMs 圆柱壳与弹性地基间的相互作用，分析弹性基础作用下FGMs 圆柱壳的振动特性[17-18]。尽管如此，很少有研究者探讨弹性介质作用下含孔隙S-FGMs圆柱壳的自由振动行为。本文利用Sanders壳体理论和Rayleigh-Ritz 法研究含孔隙S-FGMs圆柱壳在热载荷和轴向荷载作用下的模态频率，并分析非线性温升、孔隙率、S型体积分数指数和弹性基础参数等对S-FGMs圆柱壳模态频率的影响。

1 功能梯度圆柱壳的几何模型

如图1 所示，假设FGMs 圆柱壳环向均匀分布Winkler 型弹簧，弹性系数为Rw，且圆柱壳内部存在均匀分布的孔隙I模型或者非均匀分布的孔隙II模型。圆柱壳的几何参数包括：长度L、厚度h和中面半径R。分析时，圆柱壳的材料属性只沿厚度方向连续变化，圆柱壳的外表面为纯金属，内表面为纯陶瓷。取圆柱壳的中面建立如图1所示的正交曲面坐标系（x,θ,z），坐标系x、θ、z方向的位移分量分别用u、v、w表示。

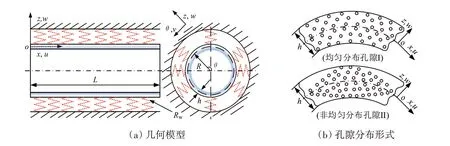
图1 含孔隙FGMs圆柱壳Fig.1 FGMs cylindrical shell with porosity

2 功能梯度材料的热物理属性

式中，N是体积分数指数，取值0≤N＜∞，V1m和V2m分别表示不同区间段的体积分数，该体积分数沿厚度方向的变化趋势如图2所示。

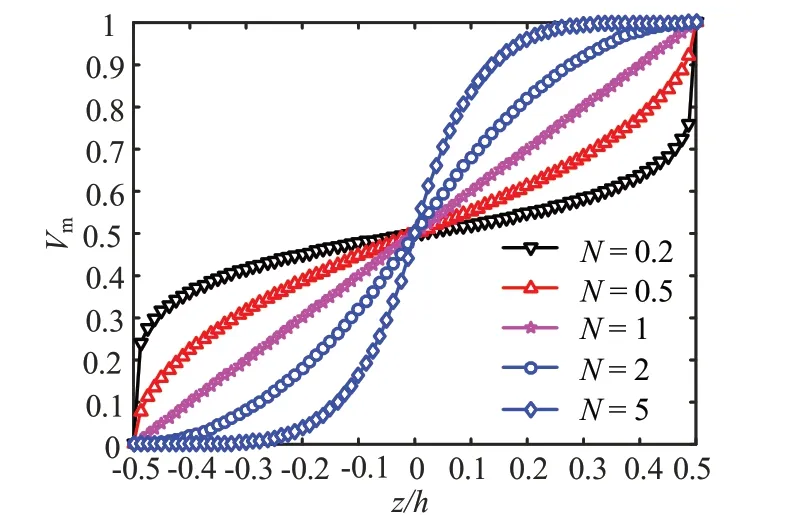
图2 S-FGMs壳分段体积分数沿厚度方向变化趋势Fig.2 Piecewise volume fraction of S-FGMs shell along the thickness direction

结合Sigmoid 型分段体积分数，S-FGMs 的有效物性参数表达式为

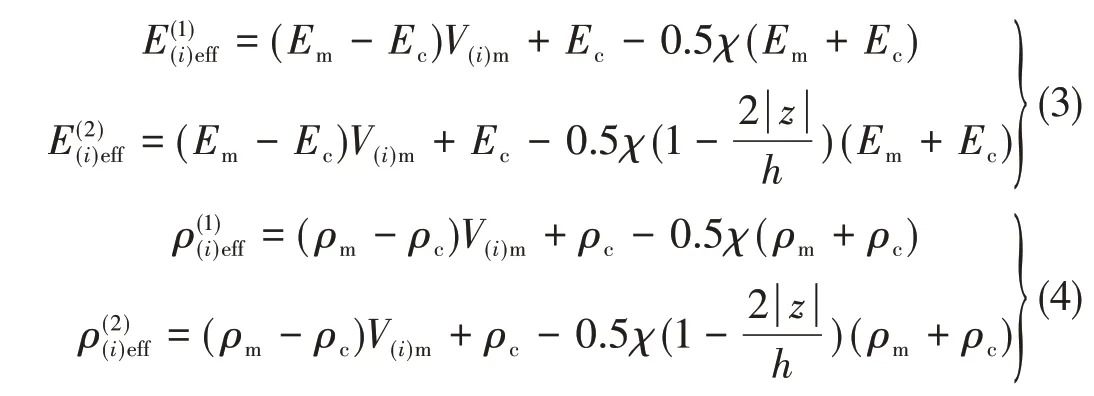
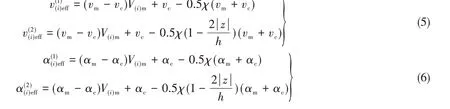
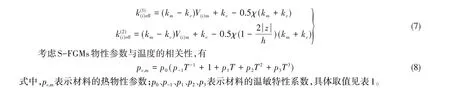
热环境下，假设S-FGMs 圆柱壳内沿厚度方向非线性分布温升，壳内表面（z=-h/2）的温度为Tc、外表面（z=h/2）的温度为Tm。取环境温度Tm=300 K，圆柱壳内部无热应力。由稳态热传导方程以及热边界条件得到沿厚度方向分布的温升T（z）为

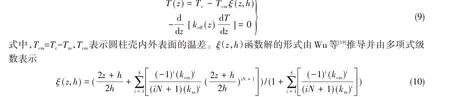
式中，kcm=kc-km，且kc和km分别表示陶瓷和金属的热传导系数。

通过式（9）和式（10）可计算S-FGMs圆柱壳沿厚度方向的温差ΔT=T（z）-Tm。鉴于弹性模量相对于热传导系数、密度等参数对S-FGMs 壳刚度的影响更大，下面只探讨非线性温升Tcm=200 K 下S-FGMs壳弹性模量与空间位置和孔隙率之间的关系。如图3所示，无孔隙S-FGMs的弹性模量总是大于含孔隙的S-FGMs，而非均匀分布孔隙S-FGMs的弹性模量基本大于均匀分布孔隙的S-FGMs。

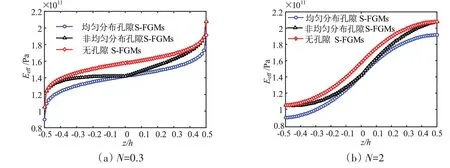
图3 含孔隙S-FGMs有效弹性模量变化趋势Fig.3 Effective elastic modulus of S-FGMs with porousity

3 S-FGMS圆柱壳的自由振动

式中，gi（i=1，…，4）为方程系数。

假设S-FGMs 壳由不锈钢和氧化锆组成，材料参数见表1。忽略环向弹性基础、温度载荷以及轴向荷载的作用，取N=1，L/R=20，h/R=0.05。基于温度控制的线性离散分层建模方法，利用Abaqus 建立S-FGMs壳的有限元模型。表2显示了无孔隙S-FGMs壳在自由边界条件下模态频率和环向波数的关系，结果表明，采用式（25）求解的模态频率与有限元求解的模态频率基本吻合，误差在一定范围内，即S-FGMs 壳模态频率方程可行。进一步地，假设FGMs 壳由不锈钢和镍组成，体积分数采用Vm=（z/h+0.5）N。取N=0.5，h/R=0.002，L/R=20，n=1，λ=mπ/L，Rw=1.5×107N/m2，图4 显示了FGMs 壳在环向弹性基础下模态频率与轴向参数λ之间的关系。结果表明，本文模型分析结果与文献[20]结果十分吻合，验证了模型的合理性。

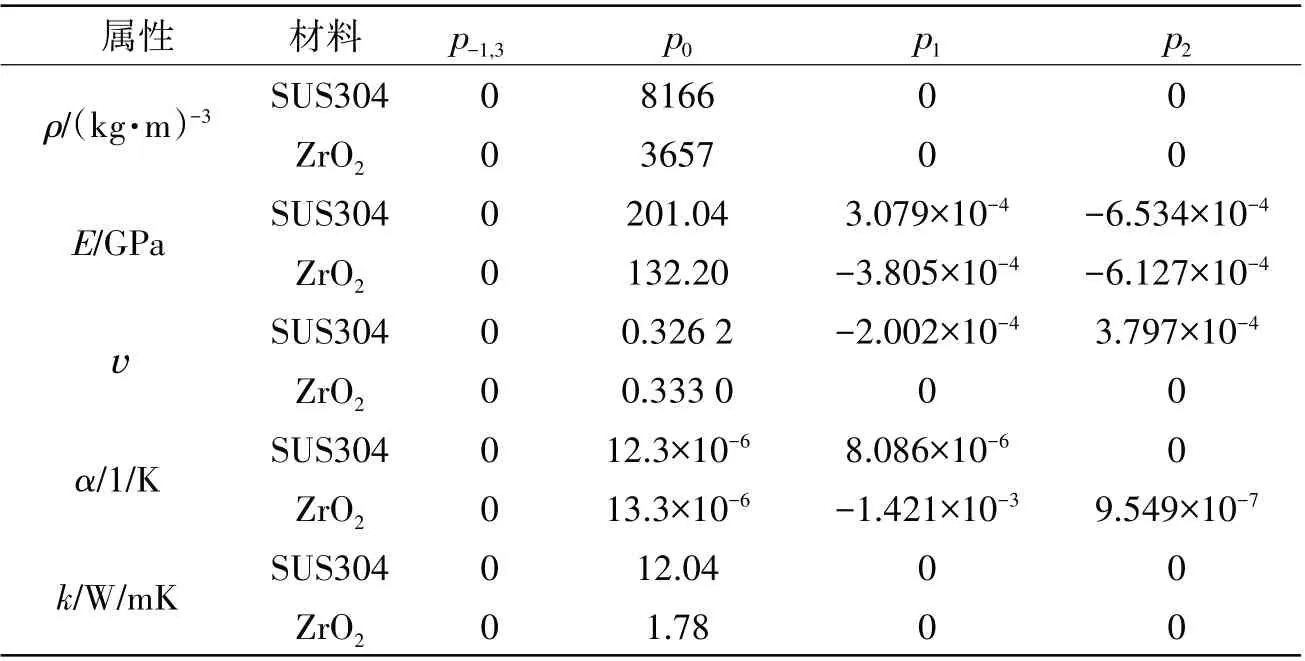
表1 ZrO2-SUS304温敏特性系数[2,4]Tab.1 Temperature-dependent coefficients for ZrO2-SUS304[2,4]

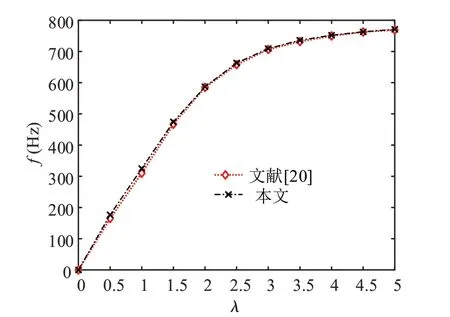
图4 环向弹性基础下FGMs壳模态频率比较Fig.4 Comparison of the modal frequencies of an FGMs shell surrounded by elastic foundation

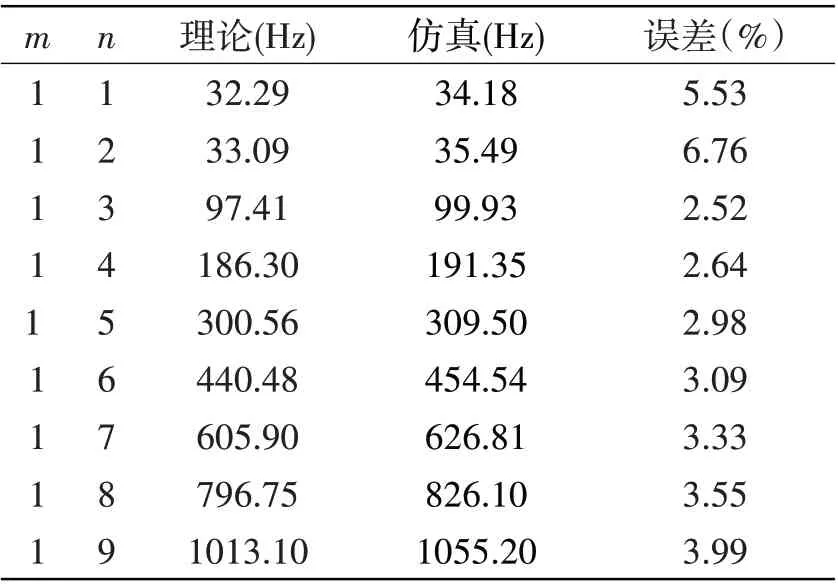
表2 S-FGMs壳模态频率对比分析Tab.2 Comparison of the modal frequencies for an S-FGMs shell

4 结果与讨论

本章以含孔隙S-FGMs圆柱壳为对象，圆柱壳由不锈钢和氧化锆组成，分析热荷载、弹性荷载以及轴向载荷作用下圆柱壳的模态频率。

数值计算时，除特别说明外，圆柱壳的几何参数均取L=10 m，h=0.01 m，R=1 m，体积分数指数N=1，温度梯度Tcm=700 K，（m，n）=（1，1）。

图5显示了不同孔隙率体积分数时，温度梯度对S-FGMs壳模态频率的影响。分析发现：

（1）χ一定时，增大Tcm会减小S-FGMs 圆柱壳的模态频率；增大振动波数（m，n）会减小Tcm对SFGMs 圆柱壳模态频率的影响；振动波数（m，n）=（4，4）时Tcm对模态频率的影响非常小，但是χ对模态频率的影响随振动波数(m,n)的增大而增大。

（2）Tcm一定时，S-FGMs 的模态频率会随着χ的增大而增大；χ为零时，I型孔隙圆柱壳的模态频率等于II 型孔隙圆柱壳的模态频率；χ不为零时，I 型孔隙的模态频率总是大于II 型孔隙的模态频率，同时I型孔隙模态频率的增长率也比II型孔隙模态频率的增长率高。究其原因，孔隙的出现对圆柱壳刚度的影响主要体现在材料的有效弹性模量和有效密度上；其中，II型孔隙模型的有效弹性模量总是大于I型孔隙模型的有效弹性模量，而I型孔隙模型的有效质量密度总是小于II型孔隙模型的有效质量密度。换而言之，I型孔隙对圆柱壳质量削减造成结构整体刚度上升的贡献大于II型孔隙弹性模量对圆柱壳刚度提升的贡献。

（3）由图3 已知含II 型孔隙S-FGMs 的弹性模量大于含I 型孔隙S-FGMs 的弹性模量，结合图5 可以说明I 型孔隙对S-FGMs 圆柱壳刚度的影响更大。分析认为，这主要是由于S-FGMs 壳内孔洞的出现类似于一种桁架结构，一定程度上孔隙率的出现不仅减少了S-FGMs 壳结构的重量，而且提高了圆柱壳的刚度。因此，设计I型孔隙圆柱壳，可为工程应用中如何降低自重和提高结构刚度提供重要的参考依据。

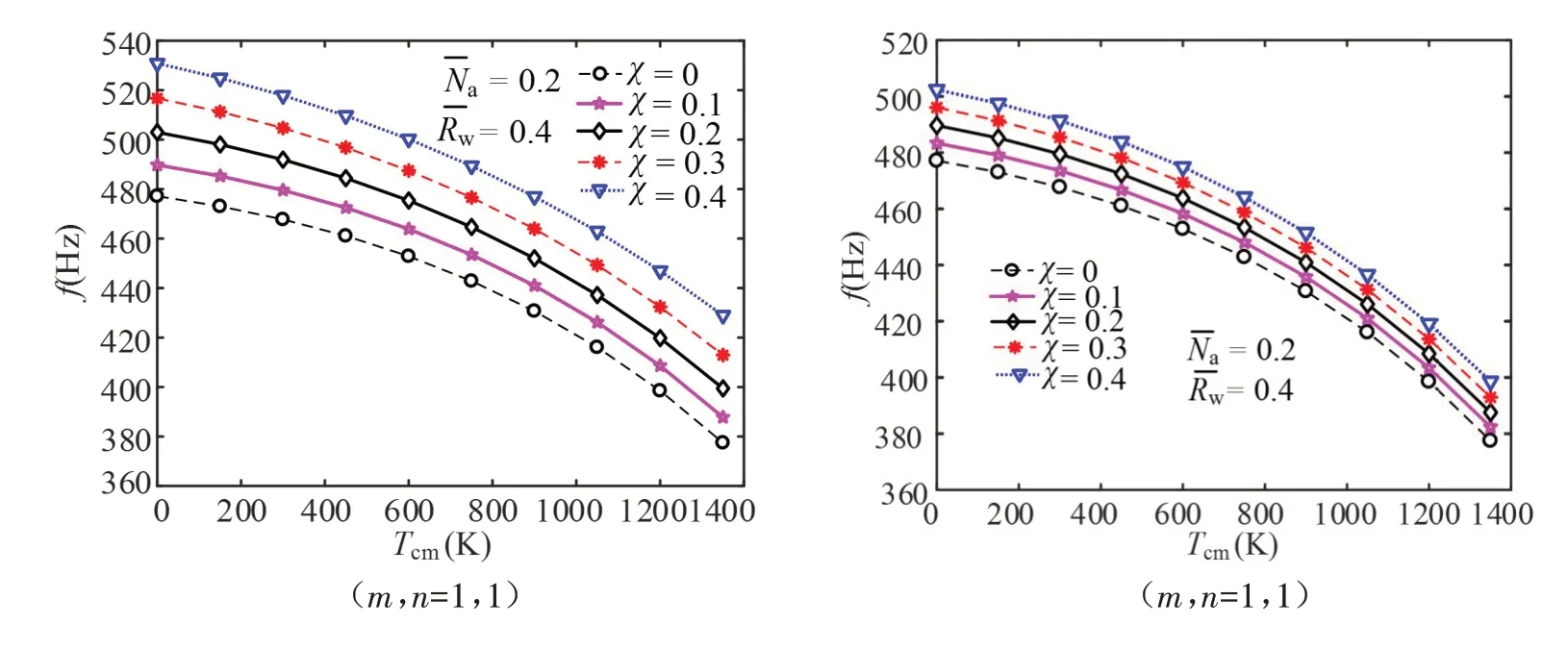
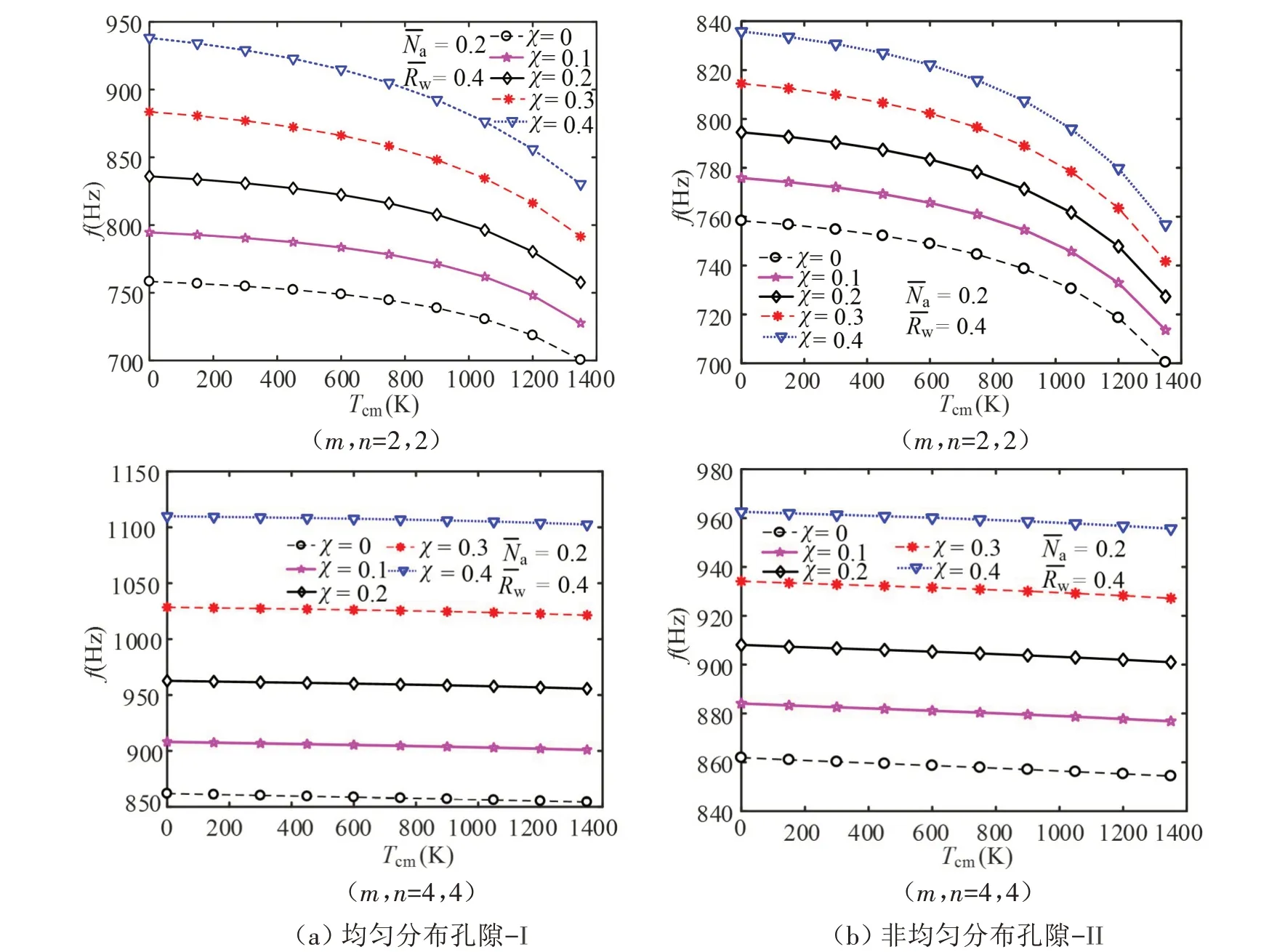
图5 不同孔隙率体积分数时温度梯度对S-FGMs壳模态频率的影响Fig.5 Effects of temperature gradient on modal frequencies of an S-FGMs shell under different porous volume fractions

图6显示了不同体积分数指数时，温度梯度对含孔隙S-FGMs壳模态频率的影响。分析表明：

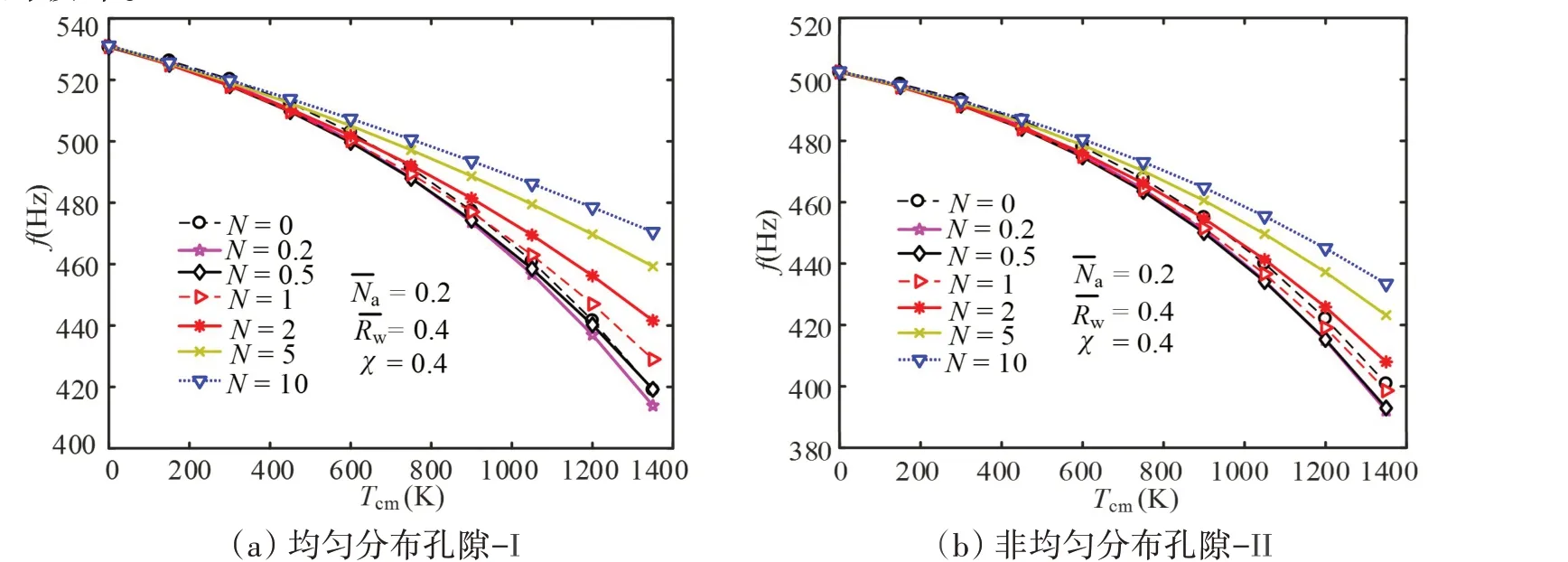
图6 不同体积分数指数下温度梯度对S-FGMs壳模态频率的影响Fig.6 Effects of temperature gradient on modal frequencies of an S-FGMs shell under different volume fraction indexes

（1）N对I型和II型孔隙圆柱壳模态频率的影响规律相似，只是在数值上有差异。

（2）Tcm较小时，N对模态频率的影响很小，N对模态频率的影响随着Tcm的增大越来越显著，且Tcm对N较小时的模态频率的影响更大。

（3）N等于0 时，垂直于厚度方向所有平面的组分含量由50%的金属和50%的陶瓷组成，对应的圆柱壳模态频率比N等于0.2时大，而比N等于1时小；随着N的增大，S-FGMs壳的模态频率也越来越大。这是因为较小的Tcm对材料内部总体刚度影响不大，模态频率基本无差异；Tcm较大时，随着N的增大，圆柱壳内表面陶瓷的含量越来越多，外表面金属的含量也越来越多；由于陶瓷的隔热性、耐热性较好，与金属比较，受热的影响更小。因此，当FGMs 应用到高温领域，采用S 型分段体积分数并增大N，不仅结构的刚度不会随着温度的升高而减小，而且组分含量中有一定量的金属具备足够的强度，能够抵抗一定的破坏。

假设轴向荷载受压为正，受拉为负，图7显示了不同轴向载荷下，温度梯度对S-FGMs壳模态频率的影响。分析表明：

图7 不同轴向荷载时温度梯度对S-FGMs壳模态频率的影响Fig.7 Effects of temperature gradient on the modal frequencies of an S-FGMs shell under different axial loads

（1）无论是I型还是II型孔隙，轴向压力Na都会让S-FGMs圆柱壳模态频率升高。

（2）当Na小于S-FGMs 圆柱壳屈曲载荷Ncr时，模态频率的变化非常小。究其原因，Na远小于圆柱壳的自身刚度，因此对模态频率的影响很小；当Na大于S-FGMs壳的Ncr且逐渐增大时，S-FGMs壳的模态频率会产生较为显著的变化，主要在于Na对S-FGMs圆柱壳刚度的影响逐渐增大并趋近于S-FGMs壳的自身刚度。

（3）I 型和II 型孔隙S-FGMs 壳的刚度随着温度的升高逐渐减小，导致模态频率逐渐减小，并呈现非线性的变化规律。

图8显示了不同弹性基础时，温度梯度S-FGMs圆柱壳模态频率的影响。分析表明：

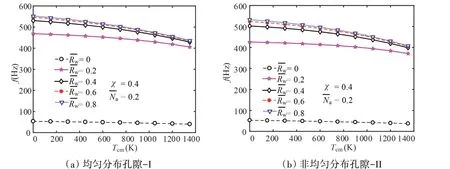
图8 不同弹性基础下温度梯度对S-FGMs壳模态频率的影响Fig.8 Effects of temperature gradient on the modal frequencies of an S-FGMs shell under different elastic foundations

（1）I型孔隙总是大于II型孔隙的模态频率。

（2）温度梯度对不同弹性基础S-FGMs壳模态频率的影响较小。

（3）含弹性基础S-FGMs 圆柱壳的模态频率是无弹性基础壳模态频率的8～10 倍。应用中，当SFGMs 壳的几何尺寸、边界条件等不便改变时，可施加弹性基础提高S-FGMs 壳刚度，防止低频共振等危害。但随着弹性基础参数的不断增大，S-FGMs壳的模态频率呈现收敛的趋势。

由于I型和II型孔隙对S-FGMs壳模态频率的影响规律相似，下文只考虑I型孔隙对S-FGMs壳模态频率的影响。图9 显示了不同孔隙率、轴向荷载及弹性基础等参数时，体积分数指数对S-FGMs 壳模态频率的影响。分析表明：

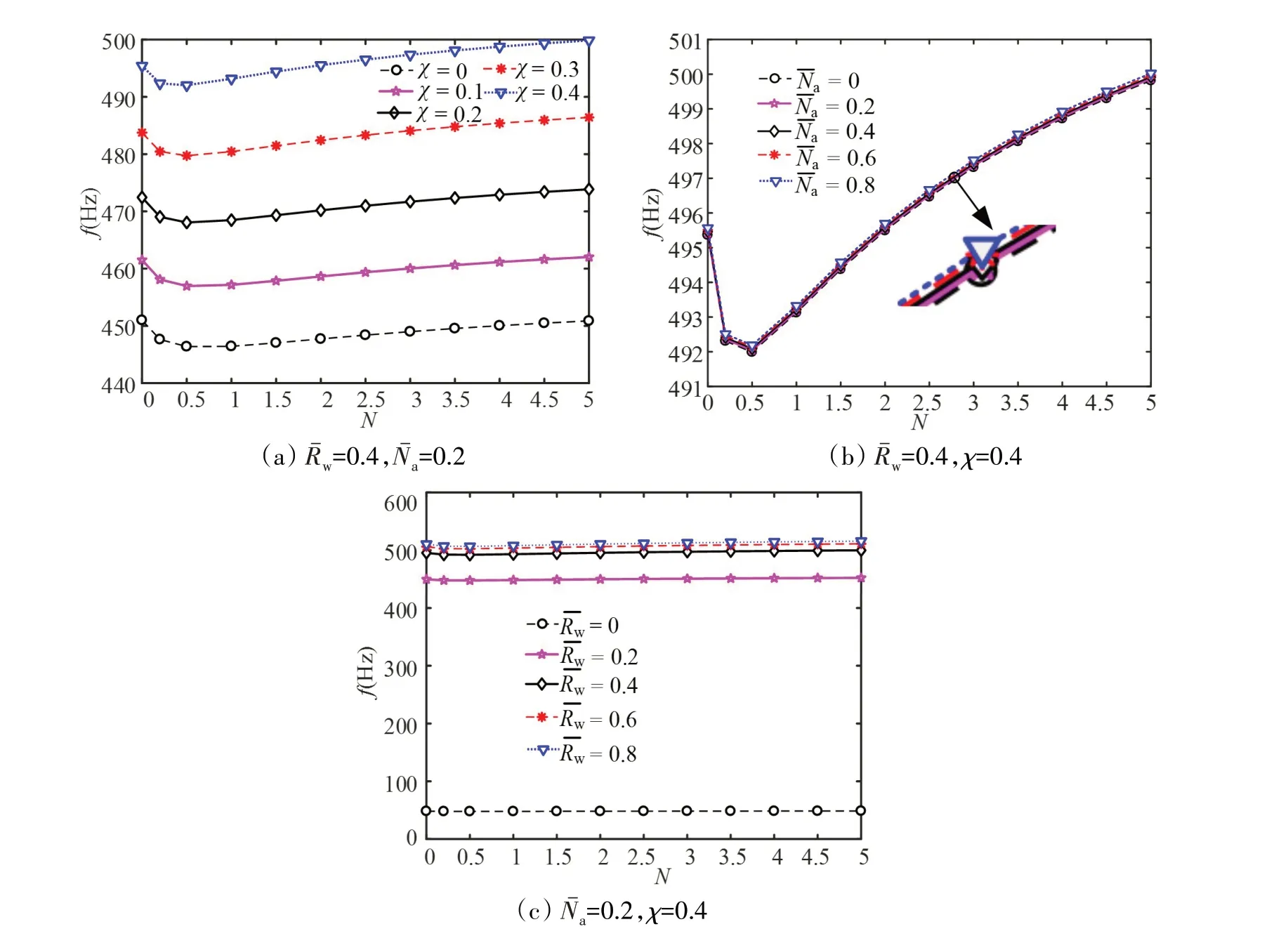
图9 不同参数下体积分数指数对S-FGMs壳模态频率的影响Fig.9 Effects of volume fraction index on modal frequencies of an S-FGMs shell under different parameters

（1）不同孔隙率和轴向荷载下，随着N的逐渐增大，圆柱壳模态频率均呈现先下降后上升的趋势，并且在N等于0.5左右时出现频率最低值。

（2）不同弹性基础参数下，N对S-FGMs圆柱壳模态频率基本无影响。

（3）调控N不仅可以提高圆柱壳的刚度和耐热性，而且S-FGMs壳模态频率的变化率很小，这说明采用S型分段体积分数材料更容易使圆柱壳结构处于稳定服役的状态。

图10分别显示了不同长径比下孔隙率、轴向荷载和弹性参数对圆柱壳模态频率的影响。分析表明：

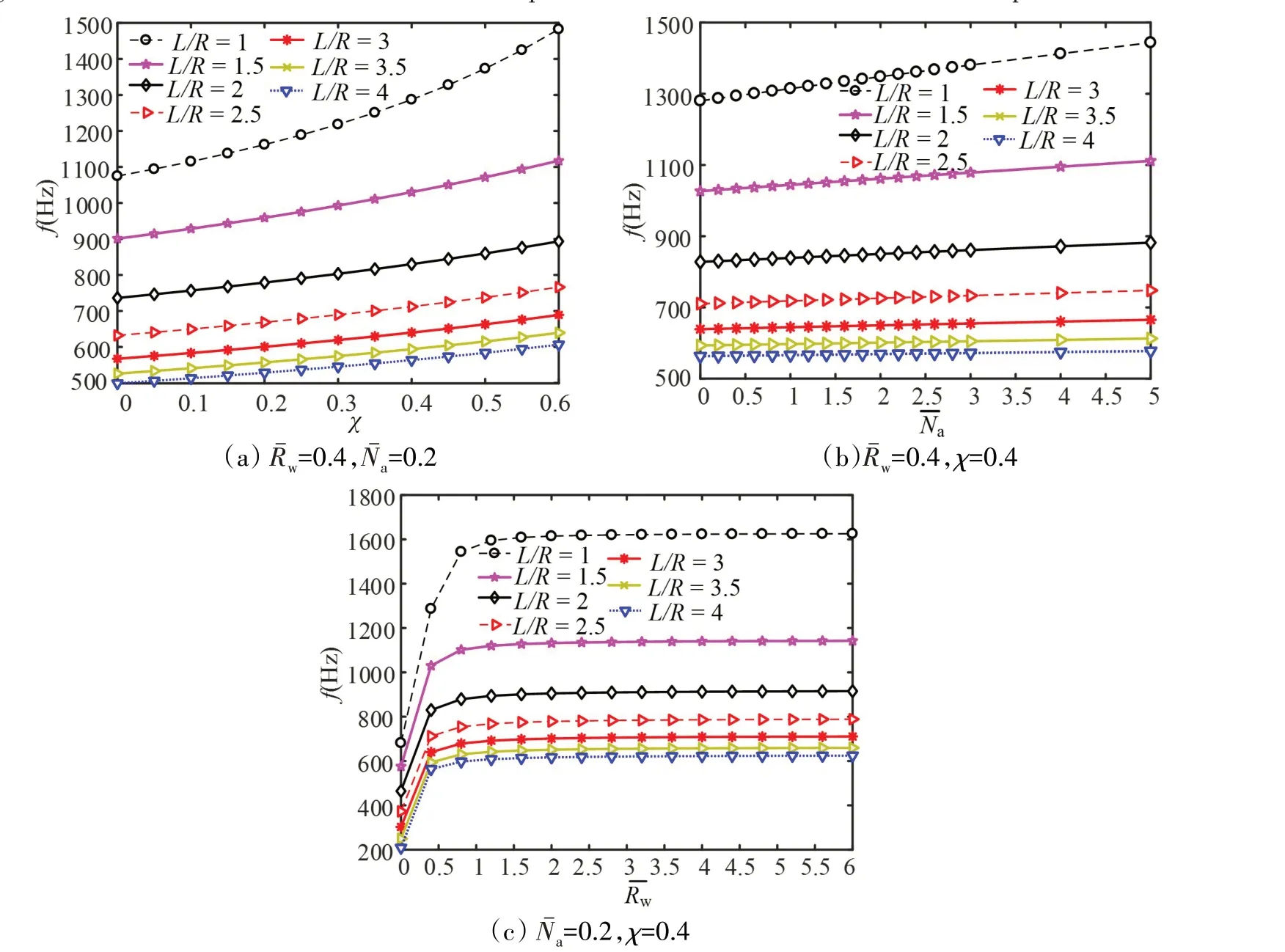
图10 不同参数下长径比对S-FGMs壳模态频率的影响Fig.10 Effects of L/R on modal frequencies of an S-FGMs shell under different parameters

（1）随着圆柱壳长径比的逐渐增大，模态频率逐渐减小且最终呈现收敛性。

（2）长径比较小时，孔隙率体积分数和轴向荷载对圆柱壳模态频率的影响更为显著。随着弹性参数逐渐增大至0.5左右，模态频率呈现快速增大后趋于稳定的规律。

5 结 论

本文基于Sanders 薄壳壳体理论和Rayleigh-Ritz 法推导了含孔隙金属陶瓷功能梯度圆柱壳的自由振动方程，探讨了热荷载、弹性基础以及轴向荷载作用下模态频率的变化趋势。主要结论如下：

（1）在同一孔隙率体积分数下，I型孔隙模型相较II型孔隙模型对刚度更为敏感，提高结构模态频率更为明显，工程应用中可注重采用I型孔隙模型。

（2）S-FGMs 壳在低振动波数下，温度梯度相较孔隙率体积分数对结构模态频率的影响更大，而在高振动波数下，孔隙率对结构模态频率的影响起主导地位；采用S 型分段体积分数，并增大该体积分数指数不仅能够削弱圆柱壳刚度受温度梯度的影响，而且组分含量中有一定量的金属而具备足够的强度，有利于结构长时间服役于复杂的热环境，但应避免体积分数指数等于0.5 时出现的模态频率最低值现象。

（3）对S-FGMs壳施加弹性基础，不仅温度梯度对含弹性基础S-FGMs壳模态频率的影响较小，而且含弹性基础壳的模态频率是无弹性基础壳模态频率的8～10倍，添加弹性基础有利于提高结构刚度避免低频共振，但当无量纲弹性基础增大至0.5，模态频率将逐渐趋于稳定。