一种低周疲劳损伤演化模型及裂纹成核缺口敏感性分析
2022-03-24黄小光王志强张典豪程斌亮叶贵根
黄小光,王志强,张典豪,程斌亮,叶贵根
(中国石油大学(华东)储运与建筑工程学院,山东 青岛 266580)
0 引 言
疲劳是工程结构和材料在交变载荷作用下的低应力破坏行为[1]。随着金属材料在机械、电子、航空航天等领域的广泛应用,疲劳逐渐成为此类部件的主要失效模式之一[2-5]。疲劳失效一般可分为裂纹萌生、裂纹扩展和断裂三个阶段。对于没有初始损伤的材料,裂纹萌生寿命通常占总寿命的80%以上[6]。因此,研究金属材料的裂纹萌生寿命具有重要意义。
根据应力应变与疲劳寿命的关系,疲劳通常可以分成应力疲劳与应变疲劳问题。人们根据对疲劳问题的理解,逐步建立了疲劳的材料力学、断裂力学和损伤力学研究方法,以及相应的疲劳寿命预测模型。S-N和ε-N曲线是最常用的高周或低周疲劳寿命预测材料力学方法[7-9]。断裂力学方法最著名的当属Paris 公式,用于预测疲劳裂纹扩展速率[10-11]。近几十年来,随着连续损伤力学的发展,基于损伤演化的疲劳寿命预测受到了广泛的关注[12-14]。Memon 等[15]利用损伤力学有限元方法研究了加载顺序对疲劳寿命的影响,验证了基于损伤力学有限元法的疲劳寿命与实验结果相一致;Tommy等[16]提出了一种针对关键部位进行详细的疲劳损伤分析的方法,可以大大简化工程实际问题的计算过程;基于损伤步长的概念,张彦军等[17]推导了疲劳裂纹萌生和扩展的预测公式,并对不同几何参数的2024和7075铝合金缺口板试件的全寿命进行了预测;关迪等[18]根据连续损伤力学和能量原理,提出了一种新的低周疲劳损伤演化模型,有效预测了金属材料的低周疲劳寿命。为满足工程设计的要求,疲劳构件不可避免地存在不同的缺口形状。在循环荷载作用下,由于局部的应力集中裂纹通常在结构缺口处萌生。因此,设计合理的缺口形状对提高缺口构件的疲劳寿命至关重要。谢季佳[19]使用改进的Tanaka-Mura模型揭示了梯度硬化厚度对疲劳裂纹萌生位置和寿命的影响;幸杰等[20]预测了缺口板试样在高、低周疲劳载荷下的裂纹萌生寿命;李聪成等[21]结合初始应力应变场、连续损伤力学理论、单元失效与裂纹萌生准则,构建了蠕变-疲劳交互作用下P92钢裂纹萌生的预测模型。
通过上述研究不难得知,对于必须加工缺口的疲劳试样,缺口形貌设计及优化对于提高疲劳寿命具有非常重要的意义,但即便如此,疲劳裂纹萌生对于缺口形貌的敏感性却很少受到关注。因此,本文从损伤力学理论出发,建立低周疲劳损伤演化模型,并将其编写为UMAT 用户材料子程序耦合到ABAQUS 中,模拟APL X65 钢缺口试样疲劳损伤演化规律,统计裂纹萌生寿命与最大应力的关系,分析缺口形貌对X65钢裂纹萌生寿命的影响。分析结果对含缺口疲劳构件的疲劳耐久性设计具有一定的参考价值。
1 损伤演化模型
对于受单轴交变载荷试样,材料性能劣化的主要机制是微裂纹以及微孔洞导致的有效承载面积的减少。如图1 所示,AD为材料受损时微裂纹及微孔洞的面积,A为材料无损状态下的横截面积。因此材料的损伤D可以表示为
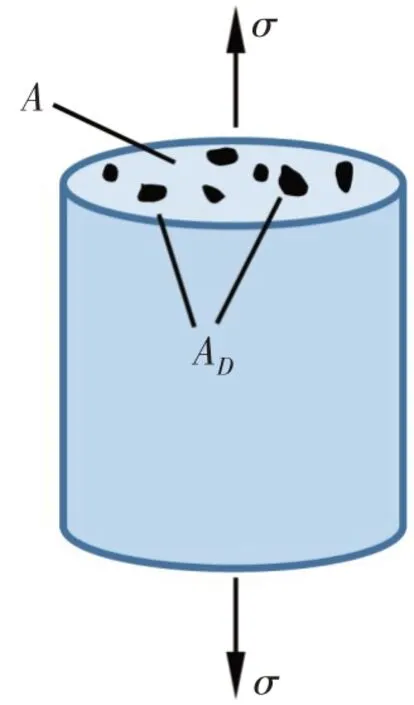
图1 单轴拉压试样损伤示意图Fig.1 Schematic diagram of uniaxial sample damage

由连续损伤力学理论可知,低周疲劳损伤通常由能量耗散势来表示,即
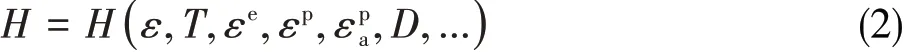


式中,Δεp表示单次循环的累积塑性应变,Δσeq表示应力幅,K和n分别为循环强度系数和循环应变硬化指数。
由于单次循环累积的损伤很小,可将式(7)中的损伤变量D看成定值,将式(7)两边微分,则可以得到塑性应变率的表达式为

假设材料初始损伤为0,裂纹萌生时,材料损伤D=1。即:N=0,D=0;N=Ni,D=1。对式(10)积分,材料低周疲劳裂纹萌生寿命可表示为

2 模型参数与损伤演化模拟
2.1 参数验证
本文以X65管道钢为研究对象,由文献[22~23]给出的低周疲劳实验数据,拟合得到上述低周疲劳损伤演化方程参数,如表1所示。

表1 X65管道钢材料参数Tab.1 Material parameters of X65 pipeline steel
利用拟合所得的损伤参数,借助FORTRAN语言将损伤演化方程编写为UMAT 子程序,并耦合到ABAQUS 有限元软件中。如图2 所示,UMAT 子程序的实现主要分为以下几个部分:参数输入、失效判定、应力应变场计算以及损伤计算。模拟过程中,ABAQUS 调用UMAT 用户子程序,首先将用户预设相关材料参数传递给子程序;计算开始之前,判定单元是否达到失效条件(本文认为D=1时为裂纹萌生的临界条件),若达到则直接结束,若未达到则继续计算相关应力应变;再根据计算所得应力应变结果得到单次循环的损伤增量∆D;当循环次数较多,为减小计算量,可将每N次循环内的损伤增量视为相等,这样程序每循环一次代表实际N次载荷循环;最后,将所得计算结果存储于状态变量,并在每次循环结束时返回ABAQUS 主程序,直至达到失效条件。这里设定裂纹萌生尺寸为0.1~0.2 mm,当失效单元的尺寸达到裂纹萌生尺寸时,裂纹萌生[20]。
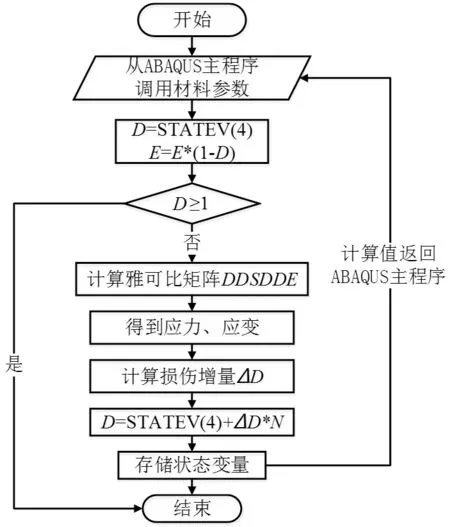
图2 UMAT计算流程示意图Fig.2 Flow diagram of UMAT implementation
利用以上原理,模拟文献[23]中各加载条件下的低周疲劳损伤演化,裂纹萌生寿命模拟值与试验值误差对比如图3所示。由此可以看出,模拟所得X65 管道钢裂纹萌生寿命与试验数据吻合较好,验证了拟合参数的合理性以及UMAT实现过程的正确性。
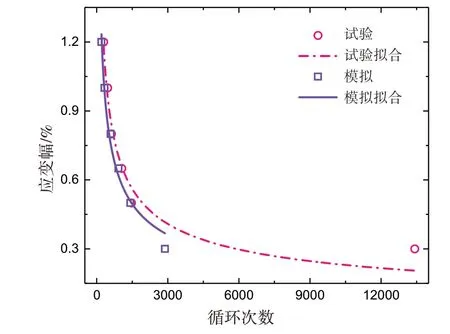
图3 X65钢裂纹萌生寿命模拟值与试验值对比Fig.3 Comparison in simulation and experimental data of crack initiation life of X65 pipeline steel
2.2 模型建立
为研究缺口参数对X65管道钢低周疲劳损伤演化以及裂纹萌生寿命的影响,本文采用与文献[24]相同的试样尺寸,在试样两侧分别预设相同缺口,如图4所示,其中H、R与θ为描述缺口类型的三个参数,分别表示缺口深度、缺口根部半径以及张开角度。本文设计不同形态的缺口组合,以研究缺口形貌变化对疲劳损伤演化及裂纹萌生寿命的影响,如表2所示。
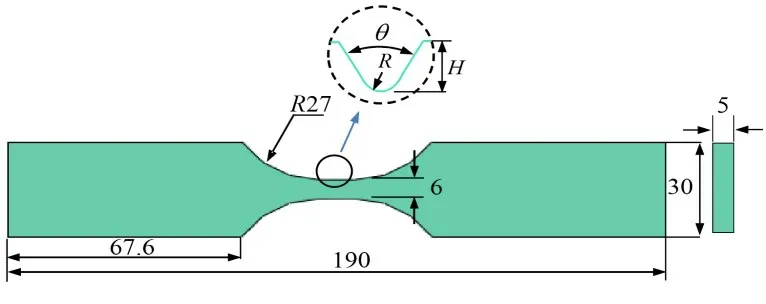
图4 缺口试样示意图(单位:mm)Fig.4 Sketch of the notched sample(unit:mm)

表2 缺口参数取值Tab.2 Shape parameters of notch
在ABAQUS有限元软件中,根据对称性建立缺口疲劳试样1/4有限元模型,如图5所示。在X方向和Y方向对称面上添加对称约束,并在试样端部施加沿X方向的交变载荷,载荷波形为三角波,周期T=4 s,应力比R=-1,最大应力为100 MPa。此外,为提高计算的精度,对试样缺口处的网格进行细化,单元类型为8节点六面体线性减缩积分单元。图6为有限元收敛性分析结果,当缺口根部局部网格尺寸小于0.02 mm 时,试样最大应力不再变化。因此在以下的有限元分析中,缺口处网格尺寸设为0.02 mm。

图5 缺口试样1/4有限元模型Fig.5 FE model of notched sample
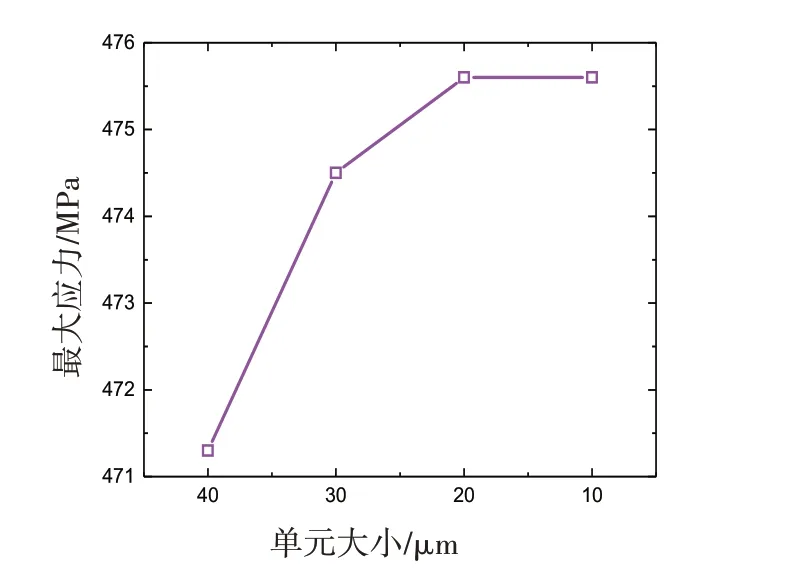
图6 收敛性分析结果Fig.6 Results of the convergence analysis
3 有限元结果与分析
3.1 参数敏感性分析
图7(a)-(c)分别显示了缺口深度、根部半径以及张开角度对裂纹萌生寿命的影响。不难看出:当缺口深度以及张开角度保持不变,缺口根部半径增大时,裂纹萌生所需的载荷循环次数也将随之增加;然而,随着缺口深度不断增加,低周疲劳损伤累积速率逐渐增大,裂纹萌生所需的循环周次也相应减少;此外,低周疲劳损伤累积也受缺口张开角度的影响,张开角度越大,疲劳裂纹萌生寿命也越长;当张开角度小于90°时,张开角度的改变对裂纹萌生寿命的影响较小,当张开角度由90°增大到150°时,裂纹萌生寿命显著增加。

图7 裂纹萌生寿命对缺口参数的敏感性Fig.7 Sensitivity of crack initiation life to notch parameters
从缺口根部中心点出发,规定沿缺口方向、厚度方向以及宽度方向分别为N、Z和Y方向。以R=H=1 mm,θ=0°缺口试样为例,研究了试样缺口处的损伤、应力及塑性应变分布,如图8所示。

图8 缺口根部损伤、应力及塑性应变分布图Fig.8 Damage,stress and plastic strain distribution near the notch root
疲劳损伤沿N方向和Y方向逐渐减小,而在Z方向上,疲劳损伤呈先增大后减小的趋势。裂纹萌生最先并不出现在缺口中心点,而是距中心位置约1 mm处。从图8还可以看出,疲劳载荷下的缺口试样损伤分布规律与应力、塑性应变分布相似,N方向和Y方向的应力、塑性应变值随着与缺口根部中心点的距离的增加而逐渐减少,而在Z方向上,缺口处应力变化不大,但总体分布趋势与损伤分布相同,呈先增大后减小的趋势。
3.2 裂纹萌生位置分析
考虑到板材厚度可能对试样裂纹萌生位置产生的影响,本文分析了双侧缺口为R=H=1 mm,θ=0°,厚度W分别为1 mm、2 mm、3 mm、5 mm、6 mm 和10 mm 的缺口试样。对比分析了不同板材厚度下,试样缺口处的应力、损伤分布规律,并考察了裂纹萌生位置与板材厚度的关系。图9显示的是不同厚度下试样缺口根部应力沿厚度方向的分布情况,图中d表示缺口部位沿厚度的距离。不难看出:随着板材厚度的增加,试样最大应力将会减小;当板材厚度小于或等于3 mm时,试样最大应力出现在缺口根部中心位置;而当厚度大于3 mm 时,其应力均将呈现先增大后减小的趋势;并且随着厚度增加,最大应力位置与缺口中心点的距离也将逐渐增大。
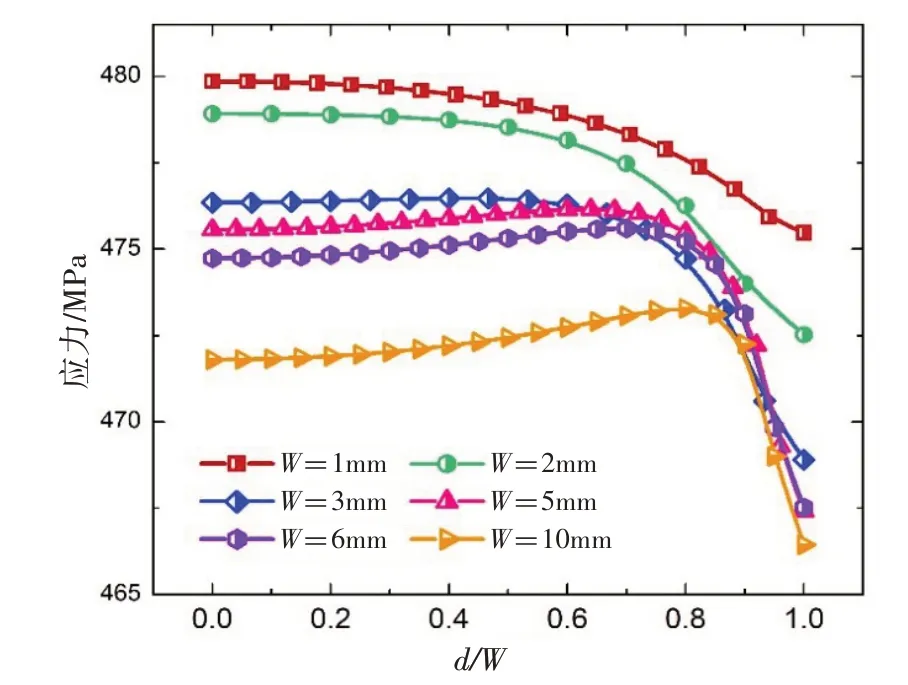
图9 板材厚度对应力分布的影响Fig.9 Influence of plate thickness on stress distribution
图10为不同厚度下试样缺口根部损伤沿厚度方向的分布情况,板材厚度对疲劳裂纹萌生位置也有一定的影响。与应力分布类似,当板材厚度小于或等于3 mm时,裂纹将在缺口中位置萌生;而当厚度大于3 mm时,裂纹萌生位置则将随着厚度的增加逐渐远离缺口中心点;并且随着板材厚度的增加,缺口中心点在裂纹萌生时刻的损伤值将越来越小。图11 所示的不同厚度下缺口根部损伤云图可以清晰地显示以上规律。当厚度W=1 mm 时,缺口中心位置损伤最先达到临界值,裂纹开始萌生,而当厚度W=10 mm时,最大损伤位置出现在靠近板的边缘处。
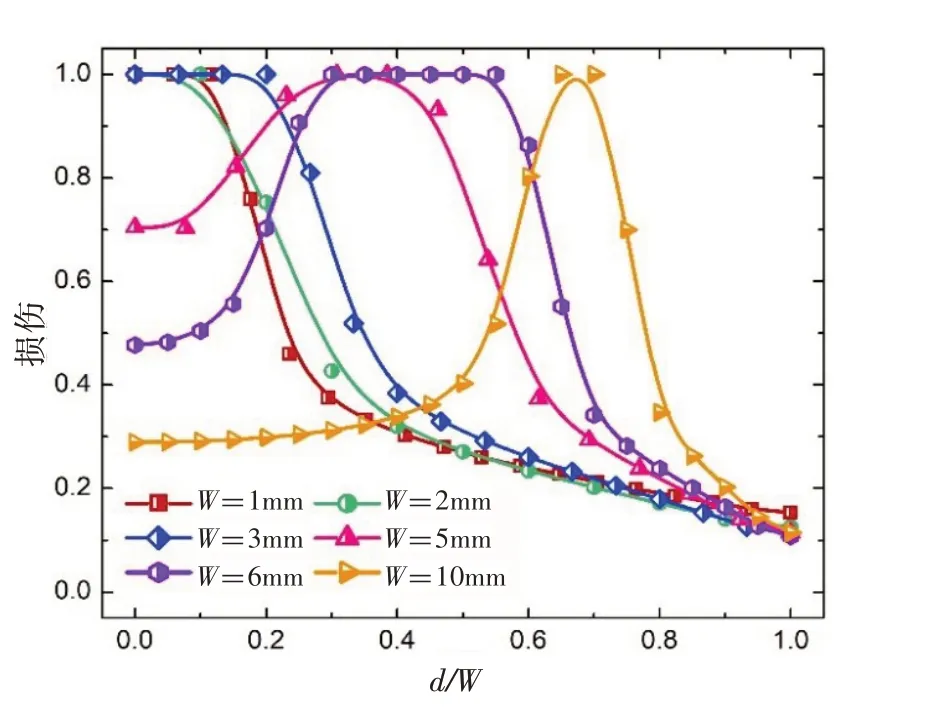
图10 板材厚度对损伤分布的影响Fig.10 Influence of plate thickness on damage distribution


图11 不同厚度下缺口根部损伤分布Fig.11 Damage distribution at the notch root with different thicknesses
3.3 最大应力与裂纹萌生寿命
图12所示为缺口试样的疲劳最大应力与裂纹成核寿命关系曲线,对比各个不同缺口试样的疲劳裂纹萌生寿命模拟结果与其对应的最大应力可知,二者可近似为线性关系,其线性关系拟合如下:
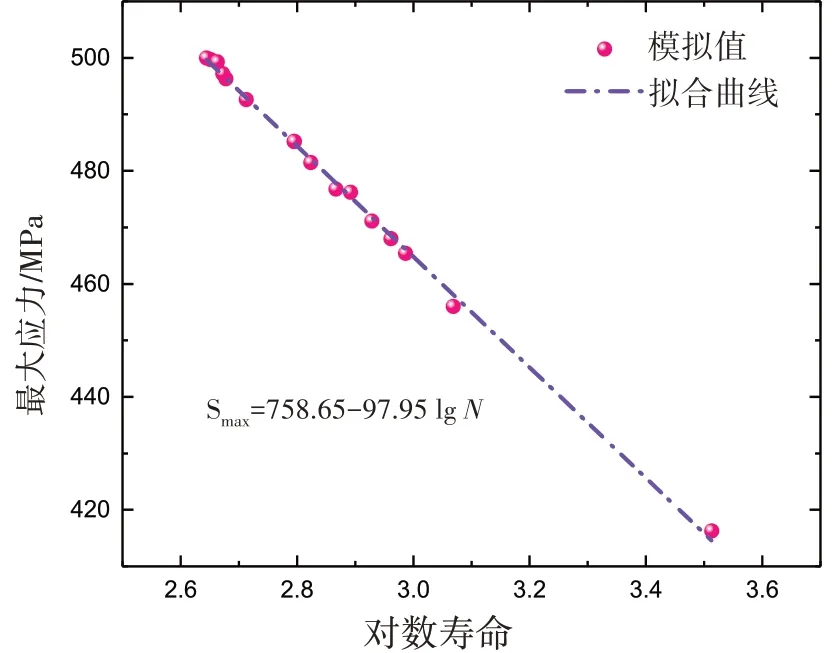
图12 最大应力/寿命关系曲线Fig.12 Maximum stress versus fatigue life

为验证上述拟合公式的正确性,本文对比了厚度分别为1 mm、2 mm、3 mm、6 mm以及10 mm时缺口试样的疲劳裂纹萌生寿命模拟结果与公式(12)的预测值,结果如图13 所示。从图中可以看出,预测值与模拟值之间的最大误差为3.7%,在工程可以接受的误差范围内,表明公式(12)能较好地预测缺口试样疲劳裂纹萌生寿命。
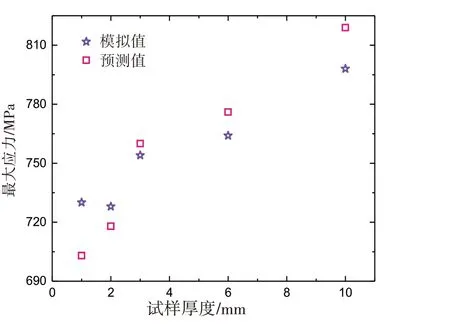
图13 疲劳寿命预测值与模拟值对比Fig.13 Comparison of predicted and simulated fatigue lives
4 结 论
本文建立了金属材料的低周疲劳损伤演化模型,通过ABAQUS软件编写损伤演化UMAT子程序,模拟了APL X65 钢缺口试样的疲劳损伤演化过程,探讨了缺口形貌对X65 钢低周疲劳裂纹萌生寿命的影响。得到的主要结论如下:
(1)缺口深度H的增大将缩短疲劳裂纹萌生寿命,而当缺口根部半径R或张开角度θ增大时,疲劳损伤累积速率将相应变慢,裂纹萌生寿命也随之延长。且当θ<90°时,疲劳裂纹萌生寿命对参数θ并不敏感,当θ≥90°时,θ的改变将导致疲劳裂纹萌生寿命发生较为显著的变化。
(2)对于同样缺口尺寸的板状试样,板材厚度对试样缺口处应力分布及裂纹萌生位置有一定的影响。当厚度W≤3 mm时,最大应力点及疲劳裂纹萌生位置均出现在缺口中心处;当W>3 mm时,缺口沿厚度方向的应力分布呈先增大后减小的趋势,疲劳裂纹也将在靠近板的边缘处萌生。
(3)拟合最大应力与缺口试样疲劳裂纹萌生寿命之间关系,得到的关系为Smax=758.65-97.95 lgN。
