波浪周期对小型船舶动力响应的影响研究

沈文君，赵志娟，刘利琴，金瑞佳，陈汉宝

（1.交通运输部天津水运工程科学研究所，港口水工建筑技术国家工程研究中心，天津 300456；2.中国直升机设计研究所，江西 景德镇， 333011；3.天津大学水利工程仿真与安全国家重点实验室，天津 300072）

0 引 言

船舶安全系靠泊并高效地进行装卸作业是港口设计和运营中的重要问题，泊位的泊稳条件不仅通过限定允许作业波高来保证，同时也考虑船舶的六自由度运动量作为安全作业标准[1]。受到防波堤掩护的港口，泊位处的波浪方向多为顺浪和斜浪，在系泊船舶六个自由度的运动分量中，横荡、纵荡和横摇是港内系泊船舶运动的主要形式，容易超出规范[2]给出的限制。系泊船舶对波浪周期非常敏感，小吨位船舶对应的固有周期也偏小，与波浪周期更易接近，系泊船舶产生大幅剧烈运动的可能性更大。而船舶运动量过大不仅影响装卸作业的效率，还易导致缆绳断缆等安全问题。因此，在港口设计和运营管理中，针对波浪周期对小型系泊船舶运动的影响开展系统研究是非常必要的，明确系泊船舶在不同波浪周期下的运动响应特性，可为设计及运营提供技术支持。

国内外已有不少学者针对波浪作用下系泊船舶的运动特性开展了研究，研究重点集中在波浪条件、船舶装载度、系缆方式和码头结构等因素对系泊船舶运动的影响，然而，针对小型船舶运动特性开展系列研究的还非常少。

Ligteringen 等[3]在分析长周期波浪作用下系泊船舶物理模型和原型测量数据的基础上，提出了长周期波浪作用下系泊船舶纵荡、横荡和横摇三个自由度运动量的估算公式。Van der Molen[4]等采用六自由度模型对澳大利亚西北部Withnell 海湾系泊LNG船舶的运动响应和系泊荷载进行了数值模拟研究，研究结果给出了涌浪作用下系泊船舶回转运动的估算公式；Van der Molen等[5-6]还采用亚长周期重力波模型，联合切片理论对日本Tomakomai 港内长周期波浪作用下的系泊船舶运动响应进行了研究，计算表明，数值计算结果与现场实测数据吻合较好，纵荡运动的固有周期与港池振荡周期接近，会导致系泊船舶的大幅运动响应；Prashant Kumar 等[7]建立了一种基于港口的几何结构以及相关波浪的绕射和折射等特性下分析系泊船舶运动的水动力模型，研究了系泊船舶在不同共振条件下不同方向的小振幅长波的运动；结果表明，入射波的方向和共振模态是分析港内固定位置系泊船舶运动的关键参数，根据波场信息，可在港口或港口站找到安全位置，指导船舶更好地进行装卸作业。

杨宪章[8]针对受涌浪和长周期波影响严重的毛里塔尼亚友谊港，对波浪和系泊船舶的运动进行了研究，研究指出，系泊船舶对低频长周期波浪响应敏感，波列中的长周期波浪成分可引起船舶的剧烈运动，从而给码头系泊及装卸作业造成危害；刘必劲[9]对20万吨级散货船和聂鸿鹏[10]对40万吨级油轮的系泊试验研究均表明船舶的运动量随着波浪周期的增大而增大；Shi 等[11]研究了横浪作用下26.6×104m3LNG 船舶的系泊运动响应特性，研究结果表明船舶的横荡运动为周期性运动，横荡自振周期与船舶横摇固有周期比值在1.11～1.23 之间，横荡和横摇运动峰值随着波浪周期的增大而逐渐增大；李越[12]利用OPTIMOOR 软件对20 万吨系泊散货船的运动进行了研究，计算结果表明，不同运动量对于波浪周期有着各自的响应特征，横荡和升沉运动随着波浪周期的增大先增大然后逐渐减小；Shen等[13]研究了波浪周期和波高对大型系泊船舶的影响，详细分析了运动随波浪周期的变化，并对危险波浪周期进行了预测，计算结果表明在横浪作用下，横摇和横荡运动占主导作用，在计算周期范围内横摇运动随着波浪周期的增大先增大后减小，横荡运动随着波浪周期的增大而增大，当波浪周期达到一定数值后，数值变化缓慢；史宪莹等[14]以一艘26.6×104m3LNG 船舶为对象，对混合波浪作用下系泊船舶的运动响应规律进行了试验研究，结果表明当混合浪能量一定时，系泊运动量大多随着低频部分波浪能量的增大而增大；沈雨生等[15]采用物理模型试验对一艘10 万吨级散货船进行了不同周期下的系列试验，研究结果表明，系泊船舶横荡运动量总体上均随着波浪周期的增大而增大，横摇和升沉运动量随着波周期的增大先增大后减小。以上工作表明，以往工程建设多以大型船舶系泊的泊稳情况为关注点，因此学者多选择大吨位船舶与波浪周期的影响关系进行研究，同时针对该耦合系统的运动频率特性开展讨论的文献较少。近几年某些小型码头的建设逐渐增多，如国内LNG运输船、国外电厂码头小型驳船或小型集装箱船等，这些船的固有周期偏小，对常见的波浪周期敏感性更高。

因此本文选取一艘小型驳船进行研究，通过对不同波浪作用角度、不同波浪周期下船舶与缆绳及护舷组成的非线性耦合系统响应特性进行模拟，旨在掌握该船舶的运动响应规律；然后通过频谱分析得到系统的频率特性，并基于小波分析，进一步了解该耦合系统在时域内的频谱变化规律。

1 数值计算

1.1 数值理论及方程的建立

系泊船舶在环境载荷、系泊载荷和护舷荷载的共同作用下处于平衡，本文通过Hydrostar软件获得频域内波浪激振力、附加质量及阻尼系数，然后基于时频转换理论，进行傅立叶变换得到时域下波浪作用力、附加质量和迟滞函数，进而在时域内建立系泊浮体的运动响应方程，如式（1）所示。

式中：[aij]为浮体的惯性质量矩阵；[mij(t)]为浮体的附加质量矩阵；[Kij(t)]为延迟函数矩阵；[Cij]为静水恢复力矩阵；[xj(t)]为浮体六自由度位移矩阵；Fwave(t)为波浪激励力矩阵，包含一阶力和二阶慢漂力；Fcurrent(t)为流力矩阵，根据OCIMF 中的流力系数计算；Fwind(t)为风激励力矩阵，根据受风面积和OCIMF 中的风力系数计算；Ffender(t)为船舶所受的护舷挤靠力矩阵，根据图1 中的护舷性能曲线计算；Fmoor(t)为缆绳拉力荷载，根据图1中的缆绳性能曲线计算。

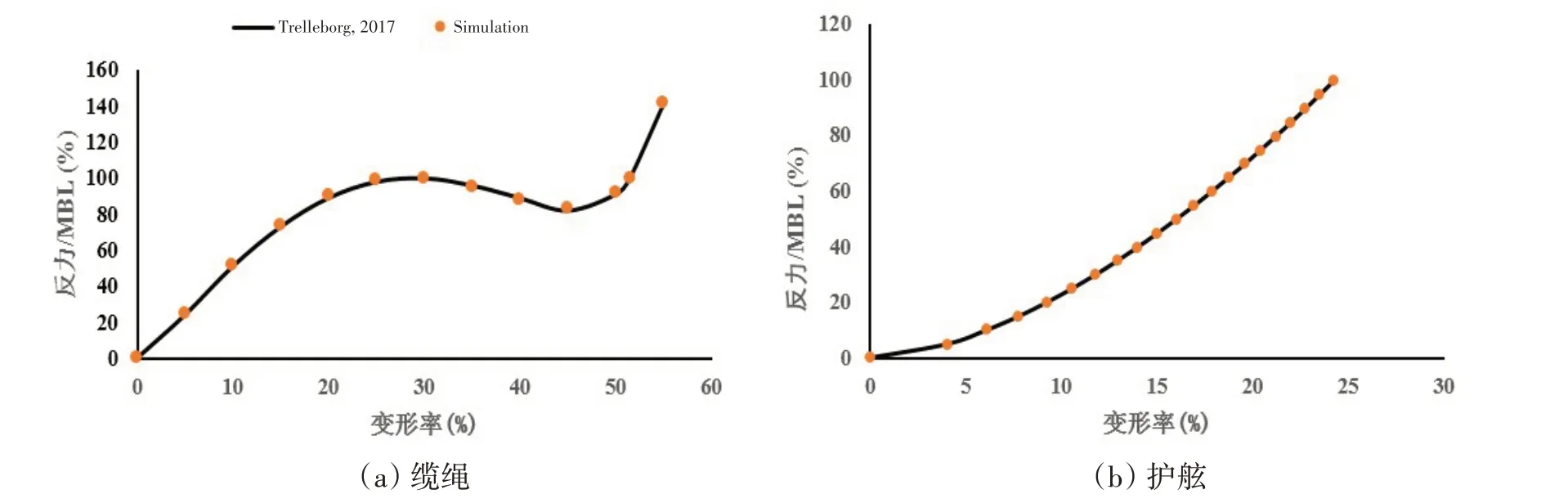
图1 缆绳与护舷性能曲线Fig.1 Performance curve of mooring line and fender

延迟函数矩阵[Kij(t)]为

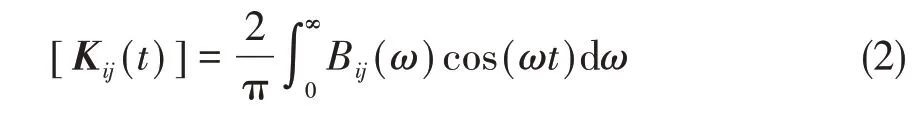
该函数可由频域水动力求解处的辐射阻尼Bij(ω)经傅里叶逆变换求出。

缆绳和护舷荷载的计算方法类似，以缆绳荷载的计算为例进行解释说明，再计算模拟的每个时间步长，计算每根系泊缆绳的系船柱至导缆孔的水平距离和方位角，方位角根据图2确定。

图2 导缆孔与系船柱之间的系泊缆绳Fig.2 Mooring line between fairlead and anchor

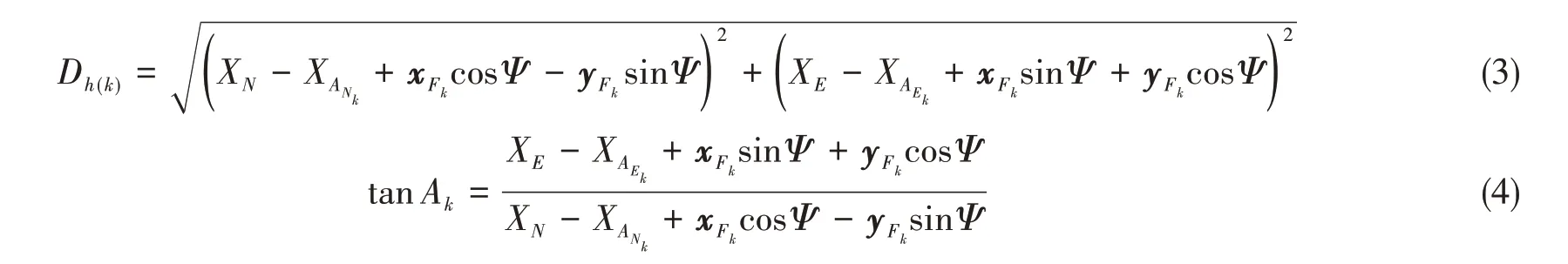
式中：xFk、yFk、zFk分别为第k根系泊缆绳导缆孔在船体坐标系中的坐标；Dh(k)为第k根系泊缆绳系船柱至导缆孔的水平距离；Ak为第k根系泊缆绳导缆孔至系船柱方向与固定坐标系N轴的方位角；XAEk为第k根系泊缆绳系船柱在固定坐标系中的坐标；(XE,XN)为坐标原点O在固定坐标系中的坐标；Ψ为船头与固定坐标系N轴的方位角。

通过式（3）计算出缆绳长度，进而得到缆绳长度的变化量，然后根据缆绳的变形与拉力曲线（图1）即可得到缆绳的拉力，将所有缆绳的拉力加在一起得到方程（1）中的Fmoor，根据同样的方法计算Ffender。

1.2 算例模型

计算所用驳船主尺度如表1 所示，水动力计算模型如图3 所示。该船系泊在码头上，码头为高桩透空结构，钢管桩直径为1.0 m，间距为10 m。考虑到这种细长体结构对波浪影响较小，因此未在Hydrostar 中建立码头的水动力模型。

图3 驳船水动力网格模型Fig.3 Hydrodynamic model of the vessel

表1 浮体主尺度参数Tab.1 Parameters of principal dimension of the vessel

缆绳为聚酰胺双编织的缆绳，直径为38 mm，最小破断力为210 kN，安全工作荷载为105 kN。选用SANPE1.1 型护舷，设计反力为1081 kN，间距为6.6 m。缆绳和护舷的性能模拟曲线如图1 所示。船舶停靠码头系泊作业时的系泊布置如图4所示。

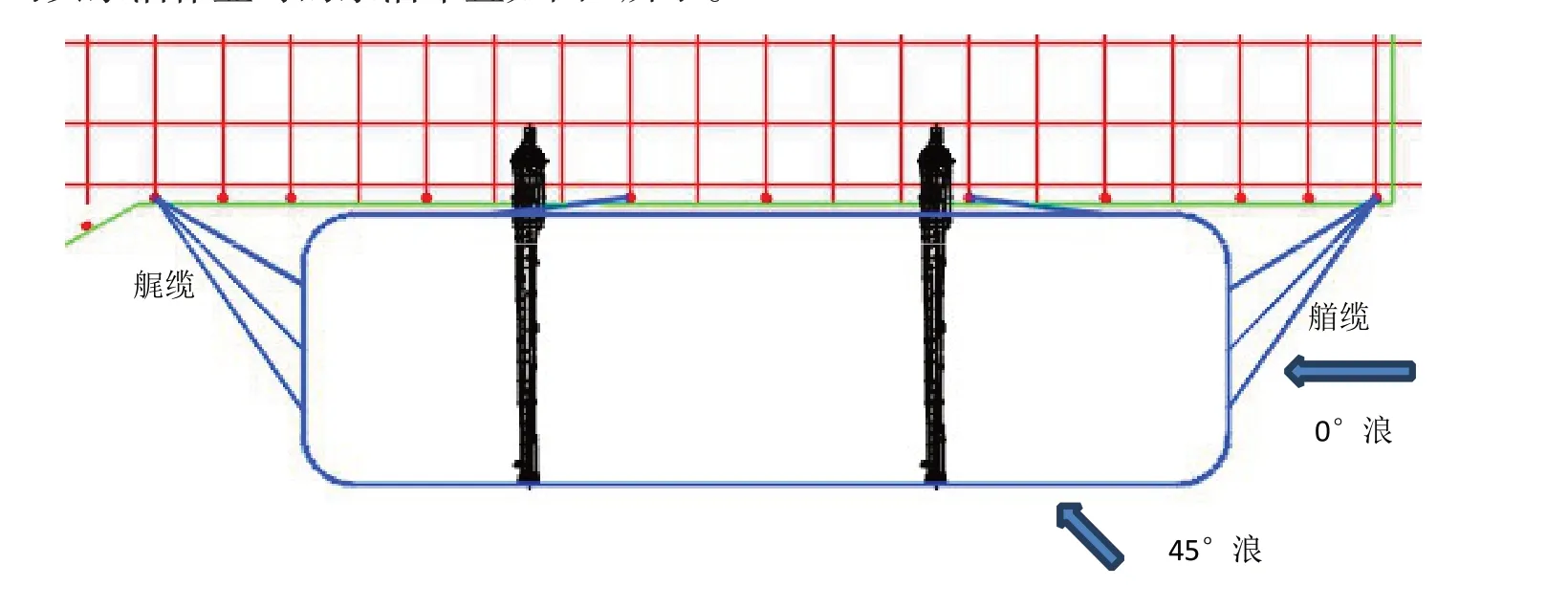
图4 作业时系泊布置方案图（3：2）Fig.4 Mooring layout plan during operation（3：2）

1.3 计算工况

试验船舶装载为满载，分别进行0°、30°和45°三种浪向下不同周期的试验组次，试验组次见表2。

表2 计算工况参数表Tab.2 Calculation cases

2 计算结果与分析

2.1 计算结果统计

Mamoun 等[16]开展了一艘液化天然气船作业于15 m 水深时的水动力荷载计算研究，对比了7个主流商业计算软件的计算结果，结果显示Hydrostar软件展现了良好的计算性能，因此本文未再进行数值验证。

将频域的水动力结果经过傅里叶变换后，代入到式（1），计算过程采用全耦合计算方法，即船舶运动响应与系泊缆的动力响应完全耦合分析，船舶波频运动和低频运动在时域范围内共同求解，进而得到船舶的运动响应曲线。图5 为不同浪向时船舶横摇和纵摇运动响应RAO，图6 为船舶在45°浪向、谱峰周期Tp为16 s时的横荡和横摇运动时历曲线。

图5 横摇和纵摇频域计算结果Fig.5 Calculation results of roll and pitch in frequency domain

将表2中的所有工况进行模拟计算，每组工况重复3次，统计分析3次结果最大值的平均值，观察船舶运动响应随波浪周期、浪向等的变化规律。

2.2 不同波浪因素对运动响应的影响

2.2.1 波浪周期对运动量的影响

按照上述统计方法，三个浪向下谱峰周期与六自由度运动量的关系如图7 所示。从图中可以看出，不同浪向下的规律基本相同，船舶的横摇运动均随着谱峰周期的增大先增大后减小再增大，三个浪向横摇运动的最大值对应的谱峰周期不同，0°、30°、45°浪向横摇运动对应的峰值周期分别在10 s、9 s、8 s附近。其他自由度基本随着谱峰周期的增大而增大。

图7 波浪周期对六自由度运动量的影响Fig.7 Influence of wave period on motion of six degrees of freedom

2.2.2 浪向对运动量的影响

在三个浪向下将六个自由度运动规律分别进行对比，结果如图8所示。从图中可以看出，横荡和艏摇运动随着波浪入射角度的增大而增大，在0°、30°和45°浪向下，波浪周期为16 s 时横荡运动分别为0.7 m、1.21 m 和2.16 m，艏摇运动分别为1.19°、1.98°和2.87°；纵荡运动在三个波浪入射角度下的结果比较接近，0°波浪对应的纵荡略大；在波浪周期为4～8 s 时，船舶的垂荡运动非常小，三个波浪入射角度下基本一致，当周期大于8 s 后，垂荡运动基本随着波浪入射角度的增大而增大，波浪周期为16 s时三个角度对应的垂荡运动分别为0.38 m、0.45 m 和0.66 m；在波浪周期为4～8 s时，船舶的横摇运动随着波浪入射角度的增大而增大，例如波浪周期为8 s时三个角度对应的横摇运动分别为0.48°、0.78°和0.97°；波浪周期为8～10 s时，30°对应的横摇角度最大，45°次之，0°对应的横摇角度最小，例如波浪周期为9 s时三个角度对应的横摇运动分别为0.67°、1.05°和0.93°，而波浪周期大于10 s后，横摇运动又随着波浪入射角度的增大而增大，波浪周期为16 s 时三个角度对应的横摇运动分别为0.66°、0.89°和1.36°。

图8 波浪入射角度对六自由度运动量的影响Fig.8 Influence of wave incident angle on motion of six degrees of freedom

2.3 频率特性分析

为了掌握船舶运动的频率特性，进一步进行频谱分析，对比了代表性周期4 s 和16 s 在0°、30°和45°波浪入射角度时对应的结果。从图9 可以看出，当受入射角度45°作用，波浪周期为4 s（0.25 Hz）时，除纵荡运动表现出明显的低频特性（纵荡固有频率）外，其他自由度的运动均以波频运动为主；波浪周期为16 s（0.062 5 Hz）时，横荡、垂荡、纵摇和艏摇的主特征频率为0.062 5 Hz，也还是以波频为主，但纵荡和横摇两个自由度的运动除了含有波频成分（0.062 5 Hz）外，还出现了明显的倍频，纵荡运动呈现出低频（纵荡固有频率）和1倍波频的特点，横摇运动呈现出2个特征频率，一个为1倍波频，另一个在0.12 Hz 附近。从图5 横摇运动的RAO 曲线可知，横摇运动的第一个峰值对应的周期在8.5 s左右，从而判断较长周期的波浪激励力不仅使系统产生了波频运动，同时，也在固有频率附近发生了振动。对0°和30°对应的结果也进行了频谱分析，与45°时的规律类似。

图9 船舶运动的频谱特性分析Fig.9 Analysis of frequency spectrum characteristics of ship motion

从上述分析可知，在较长周期时，横摇和纵荡自由度的运动不仅含有与波浪激励频率一致的成分，还含有自身固有特性的频率成分。为了进一步分析纵荡和横摇运动频率特性在时域内的变化，引入Morlet 小波变换，一般来说，任意级数ξ（t）的连续小波变换可以通过在a尺度上展开（与频率成反比）并在τ中平移母小波ψ（t）得到

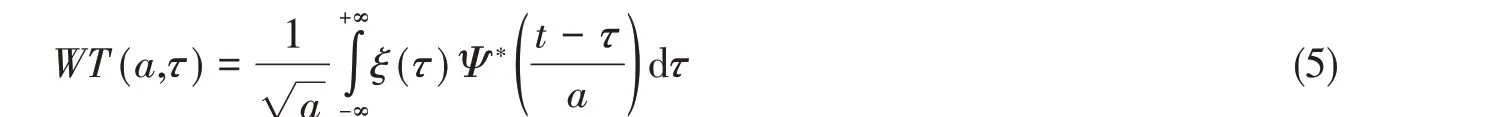
式中，星号（*）表示复共轭。计算中，选取Morlet小波作为母小波基函数，

按照上述方法，纵荡和横摇运动的小波分析结果见图10～11。从图中可以看出，系泊船舶的运动频率在较高周期时具有明显的多频和时变特性。

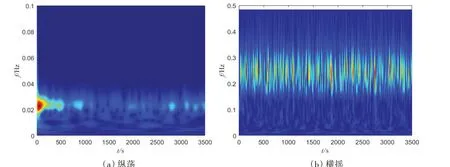
图10 Tp=4 s时，纵荡和横摇运动时频分析（45°浪向）Fig.10 Time frequency analysis of surge and roll motion with a wave period of 4 s(45°wave direction)

图10是4 s波浪周期对应的结果，纵荡运动的主要特征频率在0.03 Hz左右（纵荡固有频率），横摇运动的主要特征频率范围稍大，主要在0.15～0.35 Hz 之间（波浪频率）。图11 是16 s 波浪周期对应的结果，纵荡运动的主要特征频率有两个范围，能量较多的部分还是集中在0.03 Hz左右，能量少部分集中在0.05～0.1 Hz之间（波浪频率）；横摇运动的主要特征频率也有两个范围，两个范围对应的能量相差不太大，一部分集中在0.05～0.1 Hz之间（波浪频率），一部分集中在0.1～0.15 Hz之间（横摇固有频率），更加直观地显示了系泊船舶的时频变化特性。

图11 Tp=16 s时，纵荡和横摇运动时频分析（45°浪向）Fig.11 Time frequency analysis of surge and roll motion with a wave period of 16 s（45°wave direction）

3 结 论

为了掌握小型船舶运动响应特性与波浪周期之间的关系，本文基于频域势流理论获得了该船的水动力荷载，然后基于时频转换理论，建立了系泊船舶与护舷、系泊缆绳组成的非线性耦合系统的动力学方程，针对不同波浪作用角度、波浪周期，对该系统进行了模拟分析。主要结论如下：

（1）船舶的横摇运动均随着谱峰周期的增大先增大后减小再增大；随着浪向角的增大，横摇运动的最大值对应的谱峰周期逐渐变小；不同波浪入射角度下的规律大体相同。

（2）波浪周期为4～8 s 时，船舶的横摇运动随着波浪入射角度的增大而增大；波浪周期为8～10 s时，30°对应的横摇角度最大，45°次之，0°对应的横摇角度最小；波浪周期大于10 s 后，横摇运动又随着波浪入射角度的增大而增大。

（3）短周期波浪作用时，除纵荡外，船舶的其它五个自由度的运动均以波频运动为主，主要是波浪强迫激励运动；随着波浪周期的增大，纵荡和横摇两个自由度的运动含有双频率特征，除波浪强迫激励运动外，还存在自身的固有运动频率成分。