基于参数化水平集方法的水下耐压结构的拓扑优化

蒋垣腾，赵敏

（1.上海交通大学海洋工程国家重点实验室,上海 200240；2.高新船舶与深海开发装备协同创新中心,上海 200240）

0 引 言

随着潜水器的工作环境向着更大的深度发展，其耐压结构起到极大的作用。潜水器的耐压结构用来装载电子元件以及检测设备，为确保这些设备不会因为受到海水的压力与腐蚀而损坏，其耐压结构需要有足够的强度和稳定性。但是，其结构的质量增加同样造成总体性能的下降，因此，潜水器的耐压结构优化的目的是在保证结构强度与稳定性的条件下使结构的质量最小，并且使其结构的浮力与重力之比最大。

在以往的耐压结构设计中，常见的潜水器耐压结构有球形、椭球形、圆筒形等。采取的优化手段往往是通过尺寸优化或者简单的形状优化，尺寸优化方法主要是以结构的厚度、半径以及加强筋等的尺寸大小为设计变量进行的以轻量化等为目标函数的优化设计，形状优化则是在给定的形状下，以与设计结构物理参量无关的形状参数作为设计变量进行的结构优化设计，这类优化方式得到的结构在该形状下可以满足最优化条件。因此，究竟如何选取潜水器耐压结构的最优拓扑形式，即材料空间分布的最佳拓扑形式，有必要在常规的设计经验基础上，采用一种新的设计方法进行深入探究。目前，越来越多的设计者将目光投向拓扑优化，拓扑优化方法是一种根据给定的负载情况、约束条件和性能指标，在给定的区域内对材料分布进行优化的数学方法。在拓扑优化方法下，以结构的形状作为设计变量，通过这种优化手段，寻求得到一个满足设计要求的最佳拓扑形状。这一方法很大程度上将打破工程设计人员的思维定式，在工程实践中具有一定的指导意义。

在水下耐压结构的优化设计中，施加在结构上的载荷与传统拓扑优化设计中的固定载荷不同，该类静水压力载荷随着结构轮廓的变化而发生改变，因此，此类载荷又被称作设计相关载荷[1]。关于在设计相关载荷作用下的拓扑优化问题，其关键问题在于受力边界的搜索。

在以往的研究中，在受力边界的搜索方法上，国内外许多研究者提出了多种解决方案。2000 年，由Hammar和Olhoff[2]开创了设计相关压力载荷拓扑优化的先河，采用基于SIMP模型的变密度方法，在固体各向同性材料的灰度密度分布范围内利用贝塞尔样条曲线代表加载边界，样条曲线的控制点是由节点相对密度插值得到的等值点；2007 年，Sigmund 和Clausen[3]提出了一种混合位移压力有限元公式，其中使用重叠压力变量将空白单元定义为静水不可压缩流体；2008年，Zhang 等[4]提出了新的边界搜索算法，通过预设搜索的起点与终点，并规划压力的加载路线，直接将压力加载于结构单元边界上，并避免了载荷的灵敏度分析；2009年，Zheng 等[5]引入了伪等势函数来确定结构的边界，采用伴随法进行灵敏度分析；2012年，Lee 等[6]同样直接连接单元边界上的等密度值点作为压力作用边界，但是在设计模型中引入初始空白区域，压力则是由空白区域加载到设计区域边界上。从而，无需预先定义压力作用曲线的端点，这种方法的优点在内部受压和多压力舱的优化设计中得到了充分的体现。并且，利用高斯积分的方法将等效节点力表达为节点密度值和密度阈值的表达式，并提出了载荷灵敏度计算的解析方法。

也有研究者针对水下耐压结构设计这一工程问题，给出了解决方法。2006 年，苟鹏等[7]提出一种以柔度最小化为目标的优化算法OC-LE 法，用以解决在设计相关载荷作用下的结构优化问题，并给出外部边界受静水压力作用下的结构设计算例，证明该方法在水下耐压结构设计中的可行性；2015年，王存福等[8]提出一种基于图像分割技术的加载面搜索算法，利用Li 等[9]提出的DRLSE 模型实现图像边界探测，为了避免载荷灵敏度分析，运用了新的优化算法模型，即认为加载面在连续的一定迭代步内保持不变，并且，着重讨论了水下耐压结构的设计问题；2017年，戴扬等[10]讨论了采用不同复合材料的水下耐压结构设计问题，从复合材料的铺层方式以及角度的变化等因素，探究了复合材料在水下耐压结构设计的前景以及应用意义。

上文提到的文献都是采用密度法对在设计相关载荷下的结构拓扑优化设计或水下耐压结构设计进行的研究，密度法虽然具有较强的拓扑表现能力以及成熟的优化算法，但是由于密度法得到的结构边界过于模糊，导致在计算过程中有大量时间花费在边界搜索上，因此降低了计算效率。但是，水平集方法在优化过程中将时刻提供轮廓清晰的结构边界，这在处理表面发生多物理场相互作用的问题时具有优势，并缩短计算时间，大大提高计算效率，在工程实践中，这将缩短设计周期，具有一定的应用价值。

由于上述优势所在，水平集方法吸引了许多学者进行研究。2005年，赵康等[11]提出一种利用水平集演化技术求解设计相关载荷作用下结构拓扑问题的数值方法，由于结构的边界可以用零水平集加以描述，文中利用适当的数学变换，方便地处理施加在结构上的设计相关载荷，避免了以往算法中繁复的边界提取工作以及为了处理设计相关载荷所采取的特殊技巧；2015 年，Xia 等[12]分别利用两个水平集函数及其对应的水平集，来确定结构的压力边界以及进行水平集方法的拓扑优化，并且，为了保证优化结构的最优性，文中采用了一种周长正则化处理的方法；2019年，Picelli等[13]采用一种伪单元材料插值的固定有限网格，文中边界搜索策略是采用由拉普拉斯方程控制的流体场来计算静水压力场加载线弹性结构，并将固定网格的伪单元材料法与等效节点力相结合。

在以往的研究中，学者普遍采用传统水平集方法应用于设计相关载荷下的拓扑优化设计中，但是，传统水平集方法在处理该问题上存在一些缺陷：第一，传统水平集方法的偏微分方程的解法主要采用有限差分法，有限差分方法不适应不规则网格；第二，由于有限差分法对迭代步长的限制，因而导致寻优过程过长；第三，在结构的轮廓演化过程中，反复的重新初始化操作影响了计算效率。此外，在不考虑拓扑导数的条件下，传统水平集方法的优化结果依赖于初始结构轮廓选取，即传统水平集方法无法自行为设计结构开孔。为了提高计算效率，并提高计算结果的可信性，本文采用基于径向基函数的参数化水平集方法。参数化水平集方法由Wang 等[14]在2006 年首次提出；2018 年，Wei 等[15]提供了以柔度最小为目标的88行参数化水平集方法下的MATLAB 程序，该方法继承了传统水平集方法的优点：如结构轮廓光滑且清晰，无需重新划分网格等，将该方法应用在设计相关载荷作用下的问题可以解决传统水平集方法中在该问题上诸如需要重新初始化等的一些弊端，最为重要的是这一方法将提高耐压结构优化设计的效率。

本文将采用参数化水平集方法来解决水下耐压结构优化设计问题，研究在体积约束下不同边界约束条件下的以水下耐压结构柔度最小化为目标的拓扑优化设计。由于水平集方法中结构的边界信息隐含在水平集函数中，因此，本文提出一种边界扫描的方法，简便地提取压力边界信息，同时提出与参数化水平集方法匹配的拉格朗日算子更新策略，实现水下耐压结构的拓扑优化设计，并通过四个经典水下耐压结构设计的数值算例以证明本文方法的有效性。

1 参数化水平集方法

参数化水平集方法是指采用径向基函数插值得到的水平集函数的方法，其中，径向基函数的插值精度和插值过程中的计算效率与所选取的径向基函数的种类有关，径向基函数一般按种类分为全局径向基函数(GSRBF)和紧支径向基函数(CSRBF)[15]。

本文将采用的径向基函数为MQ（Multiquadric）样条曲线，这种径向基函数属于全局径向基函数，这种曲线用公式表示为

式中，D为设计区域，xi为设计区域的一个样本点，c为一个常数。一般而言，采用MQ 样条曲线插值的精度由样本点的选取个数与c的大小决定，本文中c取10-4。在水平集方法中，水平集函数正是一个相对结构轮廓而言的大型高维度标量场，随时间推演而变化，并且没有具体的函数表达形式。因此，将一组径向基函数分布在对应的n个样本点处，对水平集函数进行拟合，表示为

采用径向基函数对水平集函数进行插值拟合，将Hamilton-Jacobi 方程从偏微分方程简化成为一个常微分方程，将对计算产生积极影响，主要表现为以下几点：

首先，采用径向基函数插值后得到的水平集函数保证了其光滑性和连续性要求，并在其零水平集的附近能保持符号距离函数的特性，因此这种方法不需要在优化过程中反复地重新初始化，大幅减轻计算压力并提高计算效率。

其次，步长不再受限于CFL 条件，步长的选取相较于传统水平集方法更大，并得到合理的结构。这将会加快目标函数向最优解收敛的时间，并减少得到最优解所需的迭代步数。同样，这一因素将会大幅提高计算效率。

此外，在传统水平集方法中，初始设计结构的选取对最终设计结构的影响较大，而在基于径向基函数插值的参数化水平集方法中，优化结构对初始设计结构的选取依赖较小，即在这种方法下，结构在优化过程中可以自行生成孔洞，这使得优化结果更具有普遍性意义。

2 问题描述

首先，本文所讨论的问题为考虑静水压力载荷下的结构拓扑优化，为了简化所涉及的优化问题，本文在二维空间内讨论，并且讨论的问题均认为处于平面应力状态下。在设计相关载荷作用下的优化问题中，结构轮廓边界可以划分为三部分：

式中：ΓN为Neumann 边界，即压力所施加的边界；ΓD为Dirichlet 边界，即固定位移边界；Γ0为自由边界，在Γ0边界上位移不固定且没有施加外力。在优化过程中，这三种边界将随着结构轮廓的演变而变化。

结构的力平衡条件以及边界约束条件如式（7）所示：

式中，u为结构的位移场，f为结构内部的体积力，为了将问题简化，本文将不考虑体积力，即令f=0，p0（p0≤0）为Neumann边界上的压力。

本文目标函数为结构的柔度，结构的柔度等于外力在结构作用点上作的功，在设计相关载荷作用下，目标函数可以写作

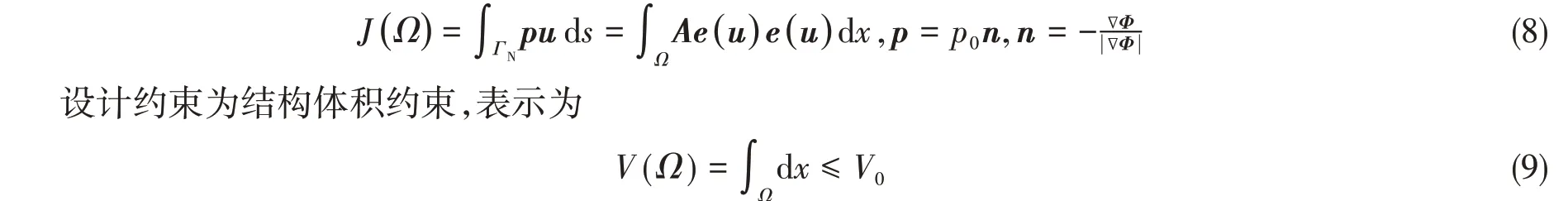
以上是本文优化问题的数学模型，设计变量为结构的形状。由于优化算法要基于梯度的下降方向，因此，本文引入形状导数的概念，关于形状导数的具体定义与定理，已有多篇文献[12,16]给出，本文将不再赘述。

3 灵敏度分析

本文将采用形状导数的理论得到Hamilton-Jacobi方程的速度场，对于优化问题的目标函数，存在两种约束：结构平衡方程以及边界条件和设计约束，即体积约束。所以，下面将逐一求解在两种约束下的速度场，即先求解在结构平衡方程以及边界条件约束下的速度场，再在此基础上，求解在体积约束下的速度场。

根据平衡方程，并通过高斯散度定理，可以得到平衡方程的弱形式为

4 体积约束处理

体积约束通过确定上文所提到的拉格朗日算子来实现，此前，有多篇论文讨论过拉格朗日乘子的选取问题，例如：采用固定拉格朗日乘子[16]，通过每一迭代步中得到的速度场求得拉格朗日乘子[11]以及采用二分法[14]求解等，这些方法得到的拉格朗日算子应用于基于径向基函数插值的水平集方法表现相对保守，收敛过程较长；针对载荷数量较大时，如设计相关载荷条件下，不能保证使目标函数在收敛过程中过渡平缓。因此，本文采用以下的拉格朗日算子的更新方法：

5 边界搜索方法以及等效静水压力载荷

为了处理设计相关载荷，需要确定载荷作用的边界，本文的搜索策略为：沿外载荷作用方向逐行或逐列进行定向扫描，在扫描方向上依次对每一个节点在与扫描方向垂直的方向进行侧向扫描，直到节点的ϕ≥0 后停止扫描，并标记为主标记点。之后再把与其邻近的单元节点标记为副标记点。只有在主副标记点上，静水压力系数p0(x)不为0。压力边界搜索实现的基本思想如图1所示。

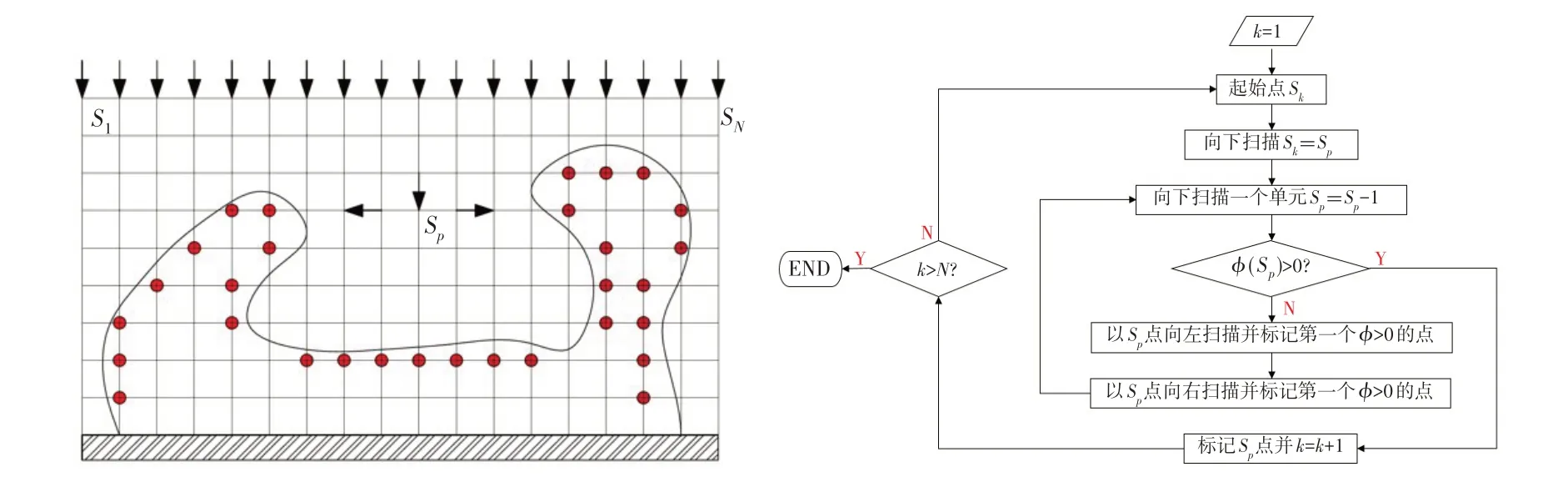
图1 静水压力边界搜索的实现方式Fig.1 Realization of hydrostatic pressure boundary search

本文提出的压力边界搜索方法可以有效解决有结构遮蔽区域的问题，得到的压力边界将更加准确。

为了准确且方便地将设计相关载荷施加在结构的压力边界上，将讨论设计相关载荷的计算方法，通过有限元分析中等效节点力的方式以及线积分转化为体积分的公式，可以得到

6 数值算例

本文的算法总结如下：

（1）初始化水平集函数，定义结构轮廓以及结构内外区域；

（2）输入一组径向基函数并对水平集函数进行拟合，从而得到这组径向基函数的插值系数；

（3）输入材料参数以及结构的边界条件；

（4）进入迭代步，检测压力边界并计算压力大小，形成有限元分析中的力向量F；

（5）组装当前结构的总刚度矩阵K，通过有限元分析得到位移场U；

（6）计算当前结构的形状导数以及拉格朗日算子，得到Hamilton-Jacobi方程的速度场；

（7）演化水平集函数，更新径向基函数前的插值系数；

（8）判断收敛性，比较目标函数在相邻5 个迭代步中的相对误差是否在合理范围内，若不满足收敛性条件，则返回到（4）。

本文通过具体数值算例来表明上述方法处理设计相关载荷作用下结构拓扑优化问题的有效性，数值算例为平面应力拓扑优化问题，杨氏模量的取值为1，泊松比的取值为0.3，编程语言为Python。

6.1 受外压拱形结构设计

本文将先通过水平集方法中的经典算例，初步证明方法的有效性。受外压的拱形耐压结构模型的设计区域、位移边界条件以及初始压力载荷条件如图2 所示，设计区域为（6 m×4 m）的矩形。结构在左右两端部附近受到固定约束，其约束宽度为0.3 m，设计材料体积为不超过设计区域的30%。设计区域的网格划分为60×40，受静水压力的大小为1。

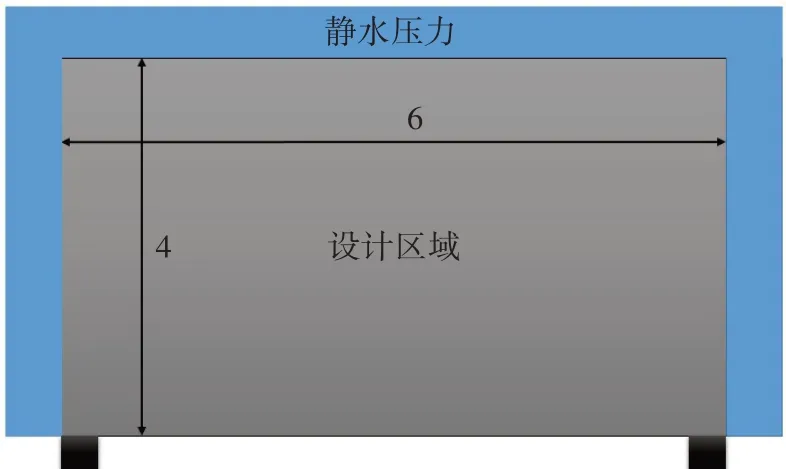
图2 受外压拱形结构设计模型Fig.2 Design model of arched structure subjected to external pressure

受外压的拱形耐压结构设计的最终结果如图3 所示，最终柔度为81.56。这一算例作为经典算例出现在中外多篇水平集方法的研究论文[11-13]中，本文得到的结构形式与以往论文相类似，算例的计算模型与赵康等[11]文中相似，赵康等对比了在初始设计域设置空洞与否以及在不同网格尺寸下的结果，得出刚度最大的结构为初始设置空洞的结果，其柔度为92.32。拓扑优化设计作为概念设计阶段的主要工具，其主要目的是为工程设计提供方案，因此在概念设计中得到的结果将极大程度影响结构的性能，这将会更好地为工程实践服务。

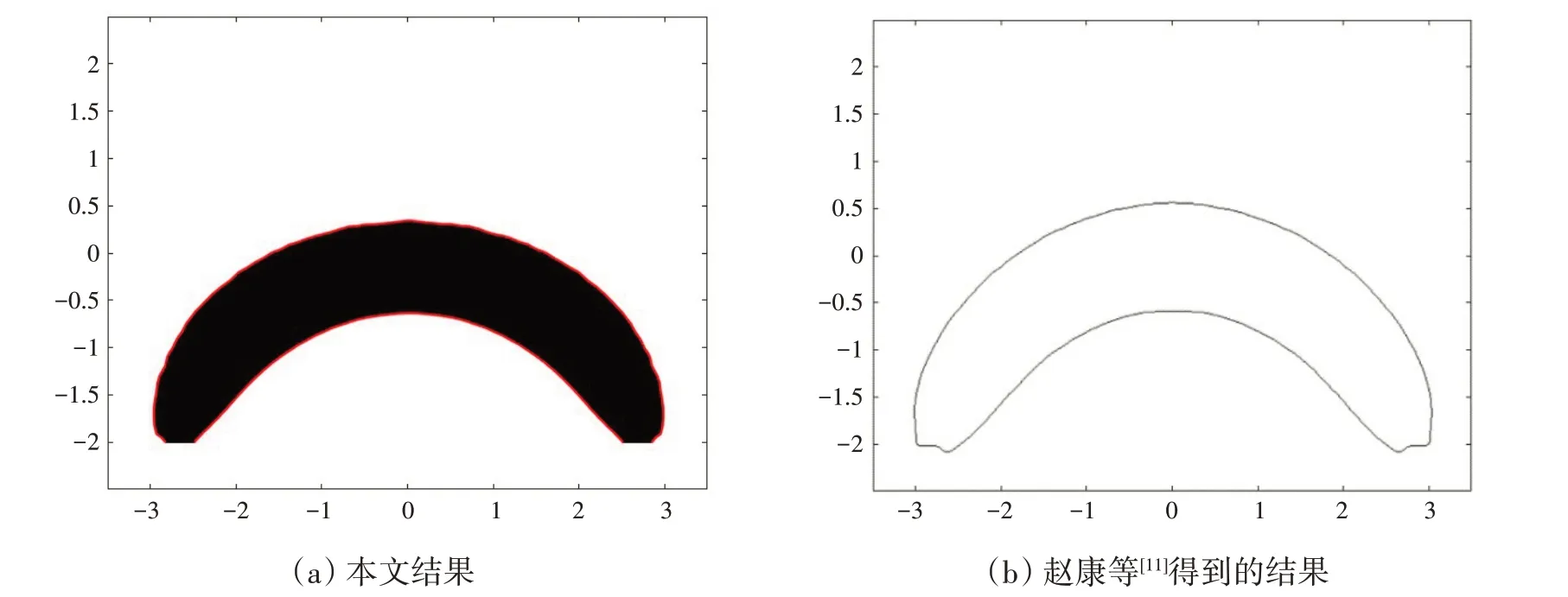
图3 本文最终结果与赵康等[11]得到的结果对比Fig.3 Comparison between results in this paper and those obtained by Zhao et al[11]

6.2 静水压力下的结构设计

耐压结构在水下工程中起到至关重要的作用，尤其是在潜水器的设计过程中。在实际工程中，耐压结构的设计需要考虑诸多方面的因素，为了方便研究，本文只在静水压力下分为两种情况进行讨论，在固定约束下受静水压力的耐压结构设计和自由约束下受静水压力的耐压结构设计，这两种情况在工程中具有应用意义，可应用于潜水器的封头以及平行中体的形状设计中。

6.2.1 在固定约束下受静水压力的结构设计

在固定约束下受静水压力的耐压结构设计的设计区域、位移边界条件以及初始压力载荷条件如图4 所示，设计区域为一个正方形（4 m×4 m），其固定约束点位于正方形中线距中心点1.5 m 处，设计约束为体积约束，最终结构的体积不超过设计区域的20%。且为了计算的简便性，本算例取用1/4 模型，设计区域的网格划分为40×40，受静水压力的大小为1。

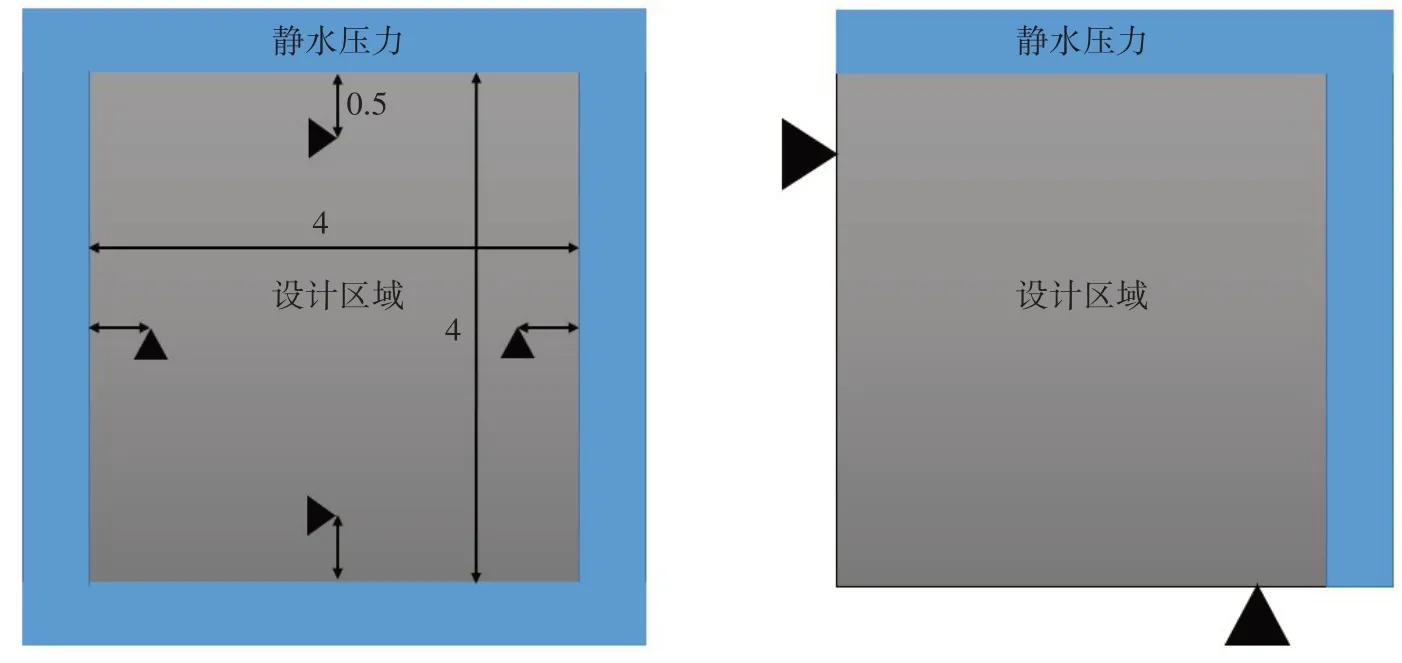
图4 在固定约束下受静水压力的结构设计模型和1/4模型Fig.4 Design model and 1/4 model of underwater pressure structure under fixed constraints

1/4 模型的结构优化结果如图5 所示，最终结构的柔度为16.41，目前本算例没有出现在以往的水平集方法的研究文章中。因此，对比在密度法下得到的结构，本文算例结果与Zheng 等[5]、Li 等[17]得到的结果类似。Zheng等[5]在文中没有给出具体的柔度值，因此，将本文的柔度与Li等[17]得到的结果相比较，在其论文中，杨氏模量取100，体积约束取设计区域的30%。在算例中提供了目标函数柔度在优化过程中的收敛曲线，再经过换算，在本文体积约束的条件下，本文结果的柔度依然小于Li 等[17]得到的结果（见图6）。

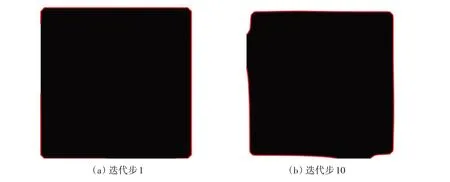
图5 在固定约束下受静水压力的结构设计的中间结果以及最终结果Fig.5 Intermediate results and final results of underwater pressure structure design subjected to hydrostatic pressure under fixed constraints

图6 本文结果与Zheng[5]等得到的结果对比Fig.6 Comparison between results in this paper and those obtained by Zheng et al[5]

6.2.2 自由约束下受静水压力下的结构设计

自由约束下受静水压力的耐压结构设计的设计区域、位移边界条件以及初始压力载荷条件如图7所示，设计区域同样为一个正方形（4 m×4 m），本算例中在正方形的两条对称轴上设计约束，限制对称轴上的区域只能在中心线方向移动，约束宽度为0.9 m，设计约束为体积约束，最终结构的体积不超过设计区域的10%。同样，为了计算的简便性，本算例将取用1/4模型，设计区域的网格划分为40×40，受静水压力的大小为1。

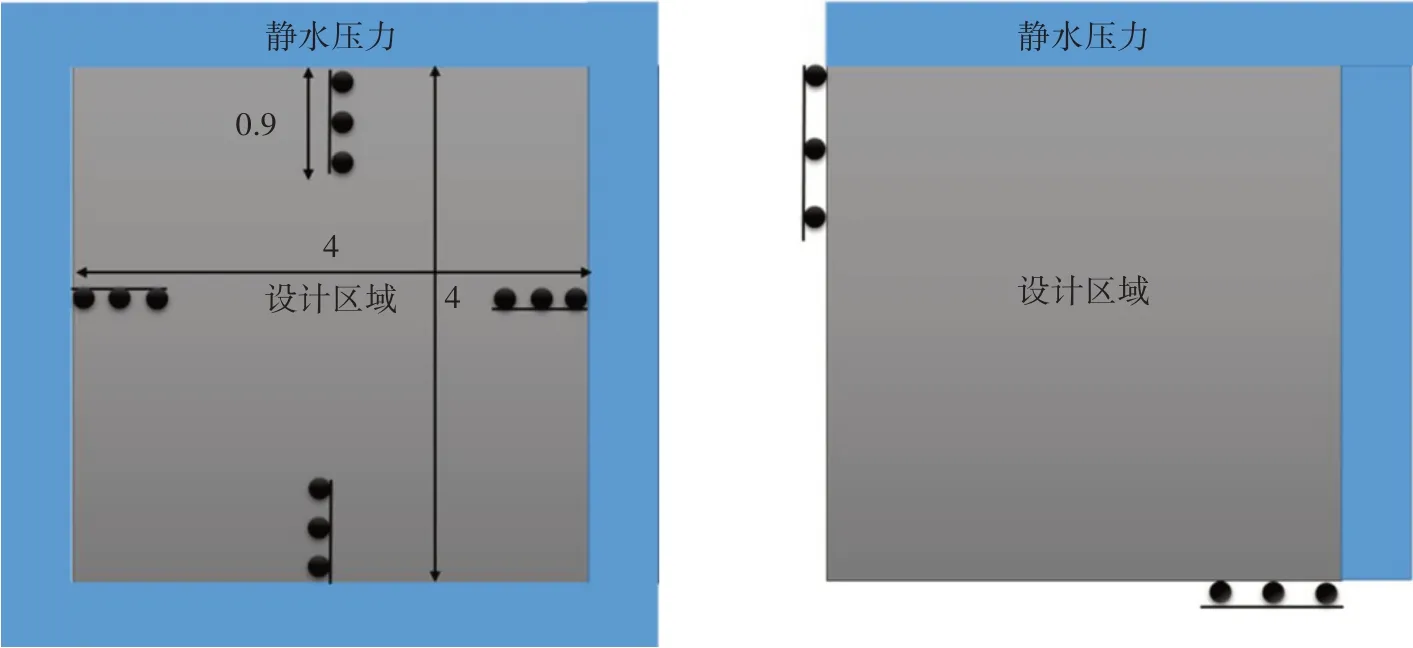
图7 自由约束下受静水压力的结构设计模型与1/4模型Fig.7 Design model and 1/4 model of underwater pressure structure under free constraints

1/4 模型的结构优化结果如图8 所示，最终结构的柔度为13.13，目前这一算例也没有出现在以往水平集方法的研究文章中。因此，对比在密度法下得到的结构，本文算例结果与王存福等[8]的论文中得到的结果完全相似，在王存福等人的论文中，取材料的杨氏模量为210 GPa，泊松比为0.3，静水压力大小取2 MPa，体积约束与本文相同，王存福等文中得到的结构最终柔度为250.15 J，无量纲化后的最终柔度值为13.15，本文结构的柔度略小于王存福等文中的柔度，得到的结构趋近于圆环状（见图9），这一结果与实际设计中采用的形状相同。

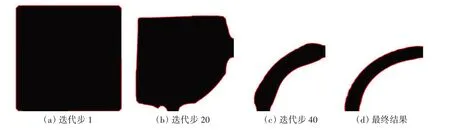
图8 自由约束下受静水压力的结构设计的中间结果以及最终结果Fig.8 Intermediate results and final results of underwater pressure structure design subjected to hydrostatic pressure under free constraints

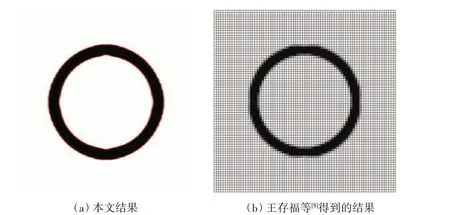
图9 本文结果与王存福等[8]得到的结果对比Fig.9 Comparison between results in this paper and those obtained by Wang et al[8]

6.3 空心水下耐压结构优化设计

在潜水器耐压结构的设计中，一般需要提供一定的储物空间，因此空心耐压结构的优化设计更加具有工程意义。与静水压力下的耐压结构设计不同，上述讨论给出了潜水器横剖面的优化形状，在本节将讨论潜水器的纵剖面的优化形状。空心耐压结构的设计模型中，在其矩形设计区域（20 m×8 m）中预留一块矩形（16 m×4 m）空白区域，空心耐压结构设计模型的设计区域、位移边界条件以及初始压力载荷条件如图10 所示，作用在设计模型上的约束在图10 中进行了标注，约束类型分为完全固定和纵向固定两种情况。设计材料体积为不超过设计区域的30%，为了降低计算压力，本算例将选用1/4模型，设计区域的网格划分为100×40，受静水压力的大小为1（见图11）。

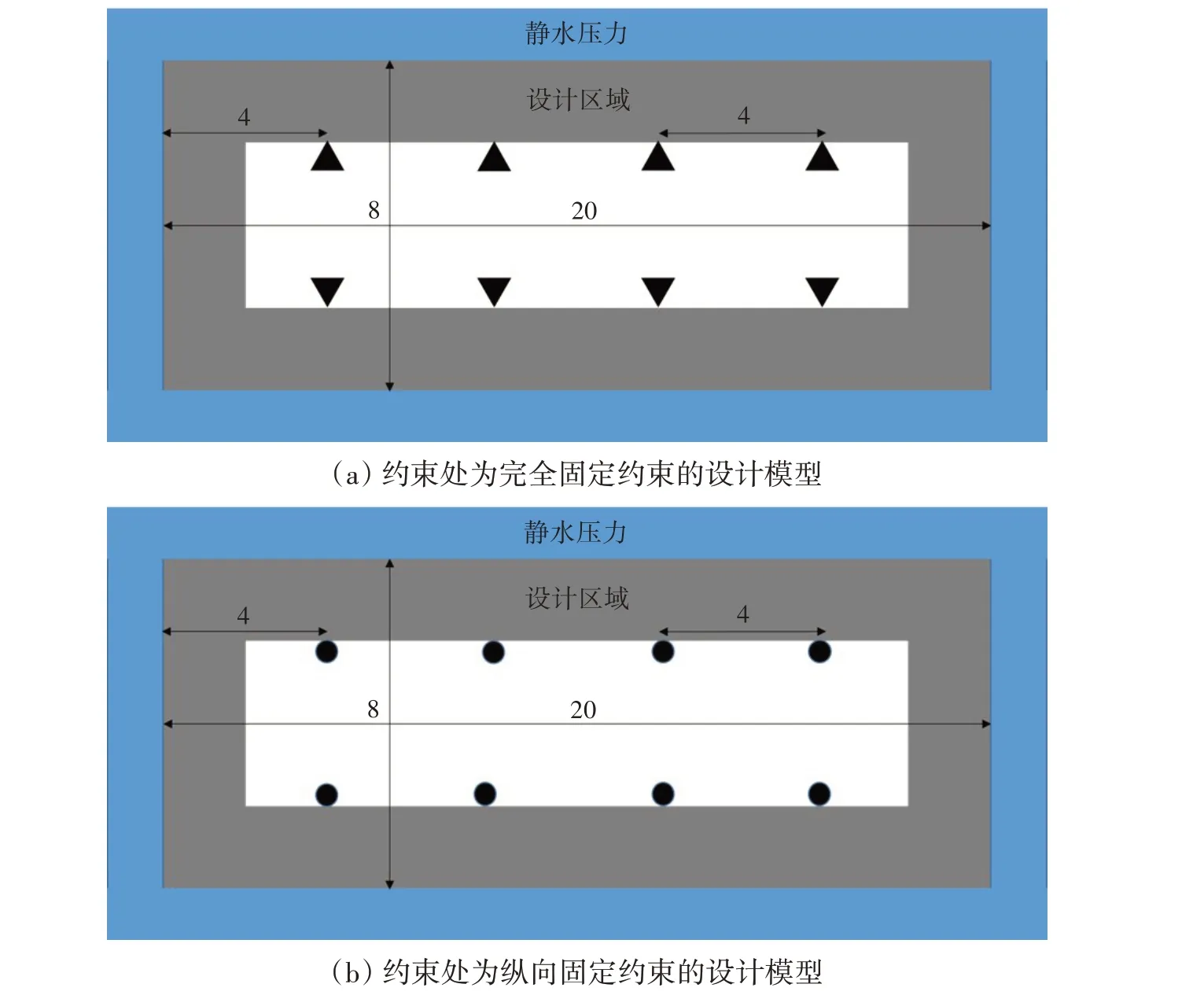
图10 空心耐压结构的设计模型Fig.10 Design model of hollow underwater pressure structure

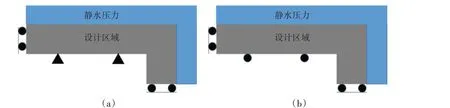
图11 空心耐压结构的1/4模型Fig.11 1/4 model of hollow underwater pressure structure

1/4 模型的结构优化结果如图12 中所示，其中图12（a）是约束处为完全固定约束的，最终结构的柔度为80.32，图12（b）是约束处为纵向固定约束的，最终结构的柔度为94.88。目前这一算例也没有出现在以往的水平集方法的研究文章中。因此，与用密度法下得到的结构进行对比，本文结果与以往论文中得到的多球交接结构在形式上类似，用Li等[17]的算例对比本文，其杨氏模量以及受力大小分别为7.0×1010Pa、10 000 N/m，其体积约束取设计区域的30%，得到的结构柔度值为0.5877 和0.6771,两个算例换算为本文单位结果分别为83.96 和96.72，本文结果与Li 等[17]得到的结构柔度值相比较小，因此，证明了本文结果的有效性。图13 中比较了本文结果与Li 等[17]的结果，图14 为MIT 水下潜水设计团队[17]提出的多球交接耐压结构模型，本文结果的结构形状与其类似，这一概念设计的提出预示着这种结构形式具有工程参考价值，且本文方法将会引导工程设计的实践。

图12 空心耐压结构设计的1/4模型的最终结果Fig.12 Final results of 1/4 model of hollow underwater pressure structure

图13 本文最终结果与Li等[17]得到的结果对比Fig 13 Comparison of the results in this paper and those obtained by Li et al[17]

图14 MIT提出的多球交接耐压结构模型[18]Fig.14 Multiple intersecting spherical pressure hull model proposed by MIT[18]

7 结 语

本文研究了考虑静水压力下水下耐压结构的拓扑优化设计问题，该问题是一个典型的设计相关载荷作用下的拓扑优化问题。由于传统水平集方法在该问题中的低效性，因而选取基于径向基函数插值的水平集方法，并利用参数化水平集方法可以得到结构轮廓清晰边界的特性，提出了一种可扫描有遮蔽区域的边界搜索方法。该方法利用了参数化水平集方法中边界信息隐含于水平集函数的特性，通过逐列或逐行扫描的方式得到了结构受静水压力的边界，可以有效并完整地得到结构的受力边界，在此基础上可以有效解决静水压力下水下耐压结构的拓扑优化设计问题。

本文重点讨论了水下耐压结构设计以及在壳体内部局部加强对耐压结构刚度的影响。水下耐压结构拓扑优化设计是以柔度最小化为目标，以结构体积为设计约束，结合改进的拉格朗日算子，在平稳的优化过程中，得到了在不同边界约束条件下水下耐压结构的优化设计结果，文中的边界约束条件是对诸如加强筋以及球壳交接处等的简化。优化结果表明，该方法可以处理诸如多球交接耐压结构等存在较为复杂边界下的水下耐压结构设计问题，经过对比可知，该方法与以往研究得到的结构形式相吻合，且得到的结构相较以往论文得到的结构具有较高的刚性。在未来新型水下耐压结构的探索过程中，该方法可以为工程设计人员的设计工作提供参考依据，具有重要的工程应用价值。

综上，本文提出的边界搜索方法在二维平面应力问题中简易且有效，为了进一步与工程实际情况接轨，接下来将针对在三维空间中的水下耐压结构设计问题、以及探究考虑应力约束下的水下耐压结构设计问题进行研究。