共轭梯度法的直观解释

何国良， 张文星， 赵熙乐

(电子科技大学 数学科学学院，成都611731)

1 引 言

数学是一门实践性很强的学科，目的是从数量关系和空间结构来研究客观对象的一些特殊属性(恩格斯、布尔巴基学派、李大潜等语). 数学成果的发现通常不是简单的灵机一动，而是需要反复实践，是建立在直观和多次失败的计算分析上，尤其是现代数学更是如此. 但和物理、化学、生物学等需要做各种各样的实验来发现新的问题不一样，数学研究主要实验方式是“思考”. 这种方式和其他学科的“硬核实验”比起来，显得比较抽象，难以理解. 实践表明如果让“思考”变得直观一些，则无论对概念、方法的理解，还是把数学作为一种工具来处理实际问题就会更加流畅. 著名数学家F. Enriques、G. Castelnuovo、J.A. Todd、小平邦彦(菲尔兹获得者)等人均认为数学的发现需要直观，需要通过“观察”数学现象来总结规律[1].

共轭梯度法(Conjugate Gradient Method)，简称CG法，是应用数学和工程领域中的一种重要方法，自该方法被研发出来以后，无论是在工程界还是在理论界都引起了大家的广泛兴趣和应用[2-5]. 目前仍然是一个非常活跃的研究话题. 人们对其不断改进，不断推广其应用场景，获得了良好的效果[6-7]，尤其是在如日中天的智能算法方面，更是起着举足轻重的作用[8-9]. 共轭梯度法已经成为理工类大学本科或者是研究生课程数值分析教学里面的一个重要内容[10-12]. 然而，由于这个方法涉及比较多、比较深的数学理论，在教学过程中我们发现，如果直接按照纯粹代数推导的方法去讲授，同学们普遍掌握不了抽象、繁琐的推导方法，或对于该方法的基本思想理解不是很透彻，就影响了该方法在实践中的应用.

本文结合多年的教学经验，从几何的角度来讨论共轭梯度法基本思想. 在此基础上，通过把代数的严密和几何的直观结合起来，比较流畅地展示了该方法“自然而然”的思维发展和递进过程，为学生进一步理解和掌握共轭梯度法提供了一种比较简单的途径.

2 基本概念

极小化方法是求函数极小值的典型方法，在工程设计、人工智能、运筹与优化、线性方程组和非线性方程组求解等方面都有广泛的用途[5，8，9]. 为避免引入过多的背景知识，这里以求解线性方程组所导出的非线性模函数(多元二次函数，参见下面定理1中的公式(2))的极小值为例来讨论共轭梯度法，这与在其他方面导出的求函数极小化方法是一样的. 下面简要介绍一下将方程组求解转换为函数极小化问题的简要过程.

设A是n阶对称正定矩阵，x，y∈n，待求解的线性方程组为

Ax=b.

(1)

若x*为方程组(1)的唯一解，则有如下重要的结果[10]：

定理1设A= (aij)n×n为n阶实对称正定矩阵，b，x∈n，则使下面二次函数

(2)

取极小值的x*是线性方程组Ax=b的解，即Ax*=b；反之亦然.

上述定理1是线性方程组与函数极小值的等价定理，通常把函数(2)叫模函数[10].根据该定理，求解线性方程组的唯一解就转换成为求模函数极小值的问题：

任取一个初始向量x(0)；

构造迭代格式:

x(k+1)=x(k)+αkx(k)， (k=0，1，2，…)，

(3)

其中p(k)是搜索方向，αk是搜索步长；

选择p(k)和αk，使得

φ(x(k+1))=φ(x(k)+αkp(k)) <φ(x(k+1))，

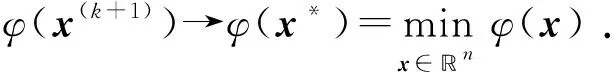
在上述的计算过程里面，关键是搜索方向p(k)的选取.实际计算中k一般取不太大的有限值，只要x(k)满足一定要求即可停止迭代.

3 共轭梯度法的一般特点

3.1 共轭梯度法的出现缘由

无论是出于工程方面的需求还是算法研究本身，都要求数值方法能迅速找到模函数(2)的极小值.由于模函数(2)是一个多元连续可微的函数，并且在矩阵是正定、对称情况下，模函数是一个凸函数，所以为迅速求模函数的最小值点，人们自然的想法就是把模函数的负梯度方向作为搜索方向，从而得到经典的最速下降法[10，12]：

算法1 最速下降法

(i) 选取x(0)∈n；

(iii) 当‖x(k+1)-x(k)‖<ε时，终止迭代.

从上面算法1可以看出，该方法计算格式简单，其搜索方向p(k)就是残差方向r(k)，整个迭代过程只需要一些矩阵和向量作代数运算即可.但实践表明，该方法整体效率可能不高，甚至对于一些对称正定矩阵，也可能存在严重的锯齿现象，如图1所示.这样一来，为了提高求解效率，人们研究发展了共轭梯度法.从上面的思路发展过程可以看出最速下降法、共轭梯度法的发生、发展情况如下：

求模函数极小值→最速下降法→需要改进→共轭梯度法

一般来说，教学活动如果按照如上过程设计，到此具有此逻辑清晰、容易理解等特点，思维也是比较流畅的.

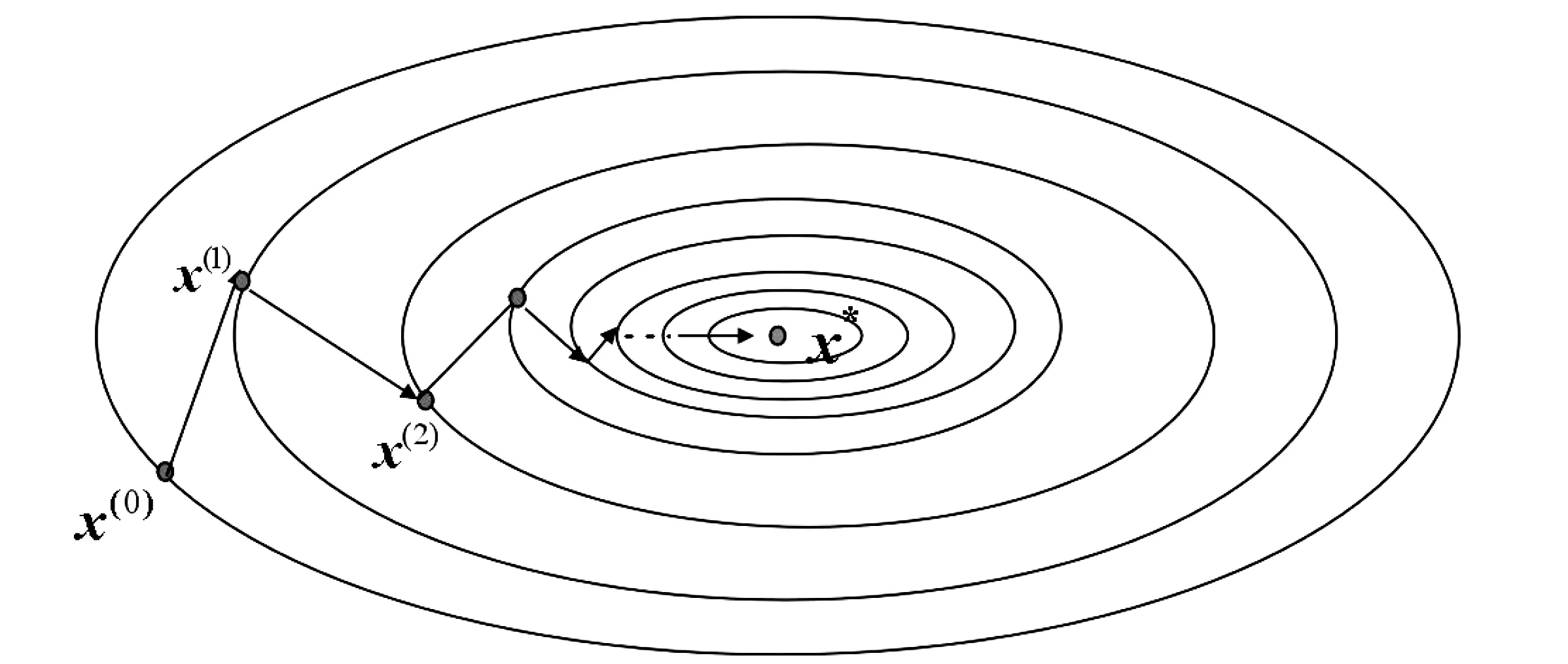
图1 最速下降法的锯齿现象

3.2 共轭梯度法的传统教学设计

从前面关于极小值的通用计算过程可以看出，极小值计算过程中，关键是公式(3)中的方向向量p(k)的选取.纵观国内外教材，由于共轭梯度法“不直观”，所以通常采用纯代数分析的角度来展开讨论选取方案——共轭(一个抽象概念)，下面简要介绍一下传统的处理方法，比如如下形式[10]：

设p(0)=r(0)，当k≥1时，对于搜索方向p(k)的确定，不但希望使

而且希望{p(k)}的选择使

由于x∈span{p(0)，…，p(k)}，则可将x记成

x=y+αp(k)，y∈span{p(0)，…，p(k-1)}，α∈.

所以有

(4)

为比较简单地计算(4)，可令

(Ay，p(k))=0，y∈span{p(0)，…，p(k-1)}，

即

(Ap(j)，p(k))=0，j=0，1，…，k-1.

(5)

公式(5)在计算过程(4)中起着重要作用，为此需要引出下面共轭的定义：

定义1设A是对称正定矩阵，若n中的向量组{p(0)，p(1)，…，p(k)}满足

(Ap(i)，p(j))=0，i≠j，

这样一来，如果将方向向量取为共轭向量组，则

(6)

对上式(6)中的第一个最小问题的解为x(k)；对于第二问题，若取p(k)，使得A(x(k)，p(k))=0(共轭)，则通过一些和最速下降法一样的简单推导，就可以到如下的共轭梯度法[10，12]：

算法2共轭梯度法

(i) 选取x(0)∈n，r(0)=b-Ax(0)；

(iii) 当‖x(k+1)-x(k)‖<ε时，终止迭代.

从前面关于极小值的通用计算过程可以看出，极小值计算过程中，关键是求公式(3)中的方向向量{p(k)}.由于模函数(公式(2))的负梯度方向在求解模函数极小值方面的意义明确清晰，并且对于对称正定矩阵来讲，其对应模函数负梯度方向刚好就是残差方向，所以无论从代数角度还是从几何角度来讲，最速下降法都容易理解.但是对于从“基”及“向量空间”的构造来介绍的共轭梯度法，虽然组织方式严谨，但是不具备良好的几何直观性，也无法向学生直观展示共轭是什么，为什么要这样选，在迭代过程中解有什么样的变化特点等.根据笔者的教学经验来看，以这种方式来介绍共轭梯度法方法，事倍功半，讲解时间花不少，但是学反应不佳.对于空间抽象思维比较好的学生，基本能够顺利理解该方法，但是对于数学基础稍弱的学生，上面的介绍过程就很具有挑战性了.

4 图解共轭梯度法

下面简要介绍从几何图形的角度来的讨论共轭梯度法，为简单起见，这里首先以二维情况来说明.

4.1 二维情况

对求解两个变量的对称正定线性方程组来讲，其对应的二元模函数，不妨记为φ(x1，x2)(注意这里的x1，x2表示二维向量的两个分量)，该函数的图形为三维空间一曲面，如下图：

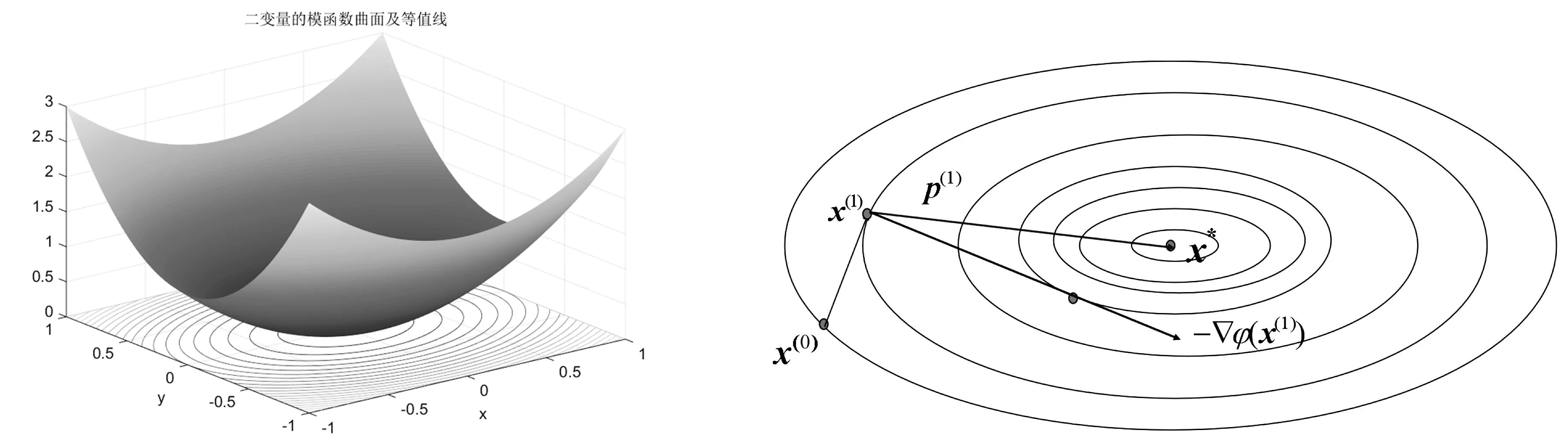
图2 二维方程组模函数曲面及在XOY坐标面的投影 图3 二次搜索计算示意图

在给定初值的情况下，为求该曲面的最小值，也选取初值的残差作为首次搜索方向.在此基础上，下面研究第二次搜索方向该如何选取——希望直接选取类似图3中的p(1)向量(直接指向最小值点)，而不是负梯度向量-▽φ(x(1))，这样总共只需要2次迭代就可以得到极小值点，从而实现高效计算.下面来看看是否能够找到这样的向量.

如果p(1)存在，希望在x(1)和p(1)的基础上，通过选择恰当的t，就可以得到

x*=x(1)+tp(1)，t∈，

其中x*表示原来方程组的解.

下面具体来看这样的p(1)是否存在.将上式带入原始的线性方程组有

Ax*-b=Ax(1)-b+tAp(1).

当A为对称正定矩阵时，由于▽φ(x)=Ax-b，所以上式可写为

▽φ(x*)=▽φ(x(1))+tAp(1).

由于▽φ(x*)=0，有

0=▽φ(x(1))+tAp(1).

在上式两端同时左乘p(0)T，有

0=p(0)T▽φ(x(1))+tp(0)TAp(1).

由于p(0)和第1次迭代的残差向量垂直，即(p(0)，▽φ(x(1)))=0，则上式变为

0=p(0)TAp(1).

(7)

上式说明什么呢？上式说明：要想两次迭代就得到线性方程组的准确解(忽略舍入误差的意义下)，那么第2次迭代中理想的搜索方向应该满足(7)式，也就是前面提到的共轭(定义1).那具体如何计算这个共轭向量呢？

对于二维问题，由于-▽φ(x(1))⊥p(0)，且三向量p(0)， -▽φ(x(1))，p(1)共面，则可将向量p(1)表示为

p(1)=-▽φ(x(1))+β1p(0).

上式两边左乘(p(0))TA，得到

p(0)TAp(1)=-p(0)T▽φ(x(1))+β1p(0)Tp(0).

由于p(0)和p(1)共轭，得

0=-p(0)T▽φ(x(1))+β1p(0)Tp(0)，

即得

这样一来，就唯一确定出第2次的方向向量.通过这样的过程，不仅从几何知道理想的方向向量是存在的，而且是可计算的.

4.2 对于三维情况

三个变量的方程组对应的模函数，不妨记为φ(x1，x2，x3)，其图形在笛卡尔坐标系下为四维超曲面.为直观起见，这里用如下的3维空间(OXYZ)来展示.图4中的左图为超曲面在Z方向取不同的值得到不同三维曲面，右图为在左图的基础上将图形沿着XOY平面的第一象限对角线条逐渐平移的结果：包括曲面和在XOY平面上的等值线变化情况.

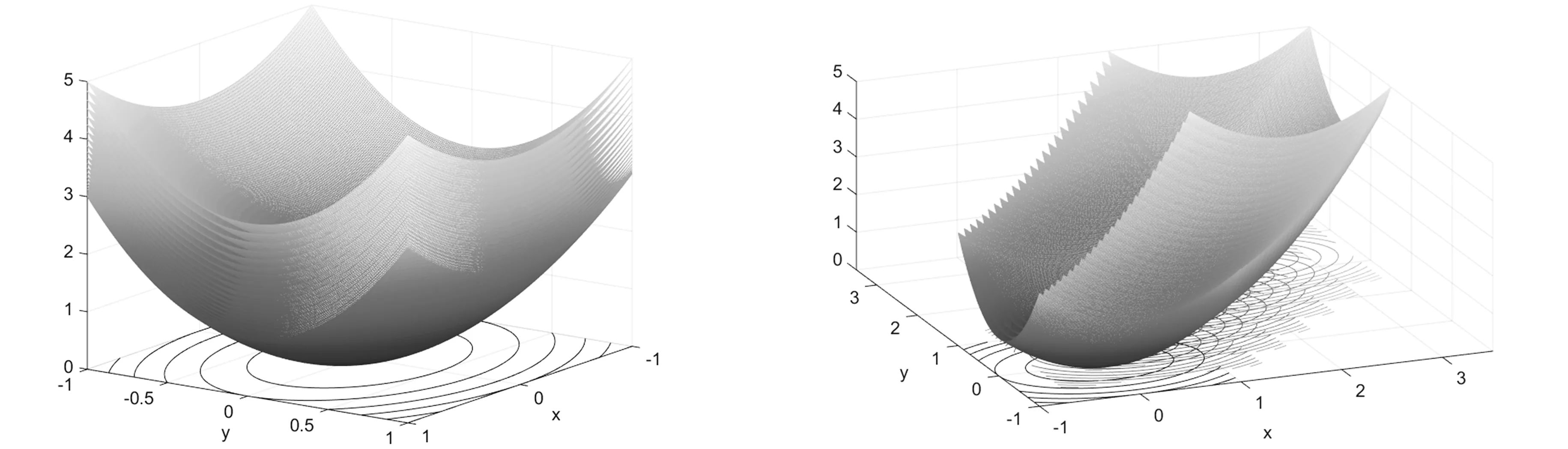
图4 三维方程组模函数曲面及在坐标面的投影

图5为三元模函数φ(x1，x2，x3)在x3=0的投影曲面和在x2=0的投影曲面，蓝色曲线为x2=0的投影曲面在XOZ平面的等值线，彩色曲线为x3=0的投影曲面在XOY平面的等值线.通过图4和图5可以从不同的角度理解模函数的基本特点.下面讨论三元函数的共轭梯度的几何特点.

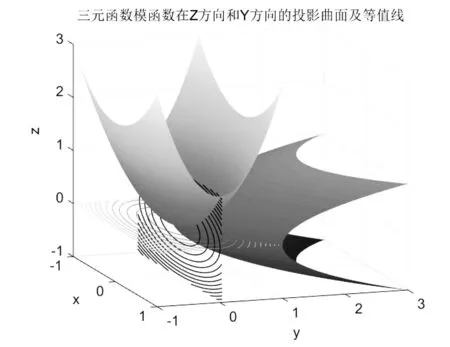
图5 三元模函数投影曲面及在坐标面的等值线投影

如图6所示，三维问题的共轭梯度法首先可以看成在超曲面的在3维空间的一个投影曲面上找一个初值x(0)，然后选取该点的负梯度方向作为搜索方向，沿着这个方向到达一个平面x(1)，这样一来，三维的共轭梯度法就被降维为变成二维的共轭梯度法(投影)，这样再运用前面二维的讨论方法就可以得出完整的三维共轭梯度法，如图6的左图和右图所示.为进一步直观，下面通过几个数值例子来进一步了解共轭梯度法的一些其他特点.

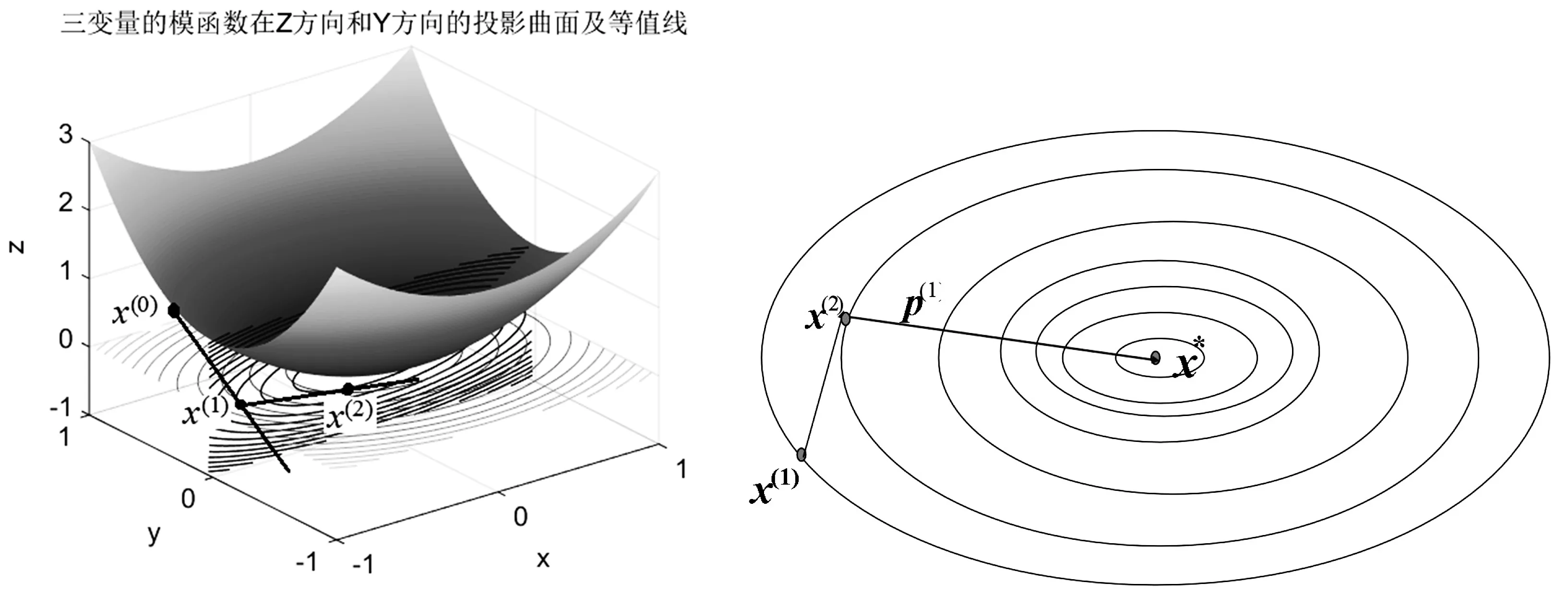
图6 三元模函数共轭梯度法搜索方向示意图

4.3 数值例子

例1利用共轭梯度法求AX=b的解.其中

该矩阵对应的模函数为

共轭梯度法计算结果如下表：

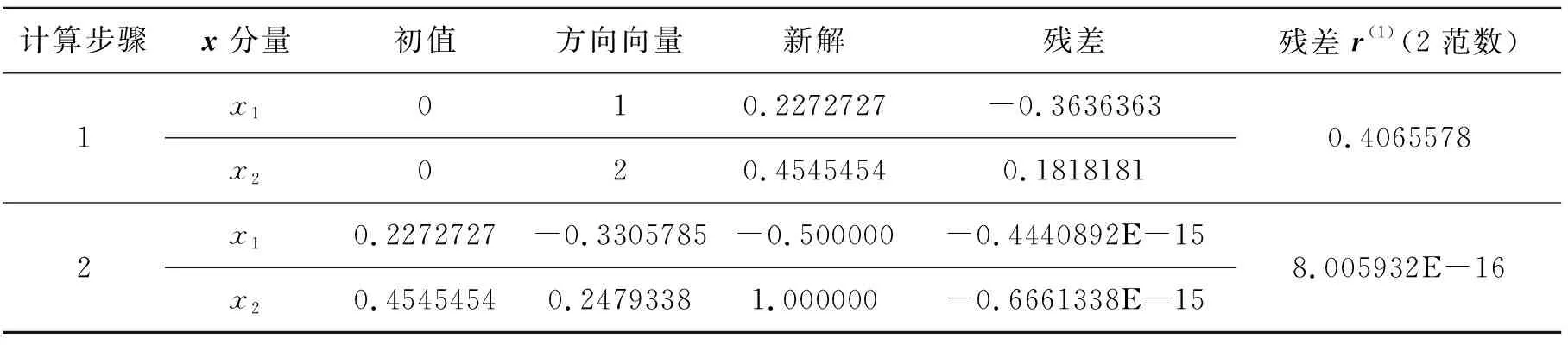
表1 2阶方程迭代情况

这里选的初值为x=(0，0)T，该问题的真解为x=(-0.5，1)T.所以在四舍五入范围内，共轭梯度法只需要2步就可以得到非常准确的结果.从计算结果来看，确实符合前面的几何解释.

例2利用共轭梯度法求3阶线性方程组AX=b的解.其中

迭代计算结果为

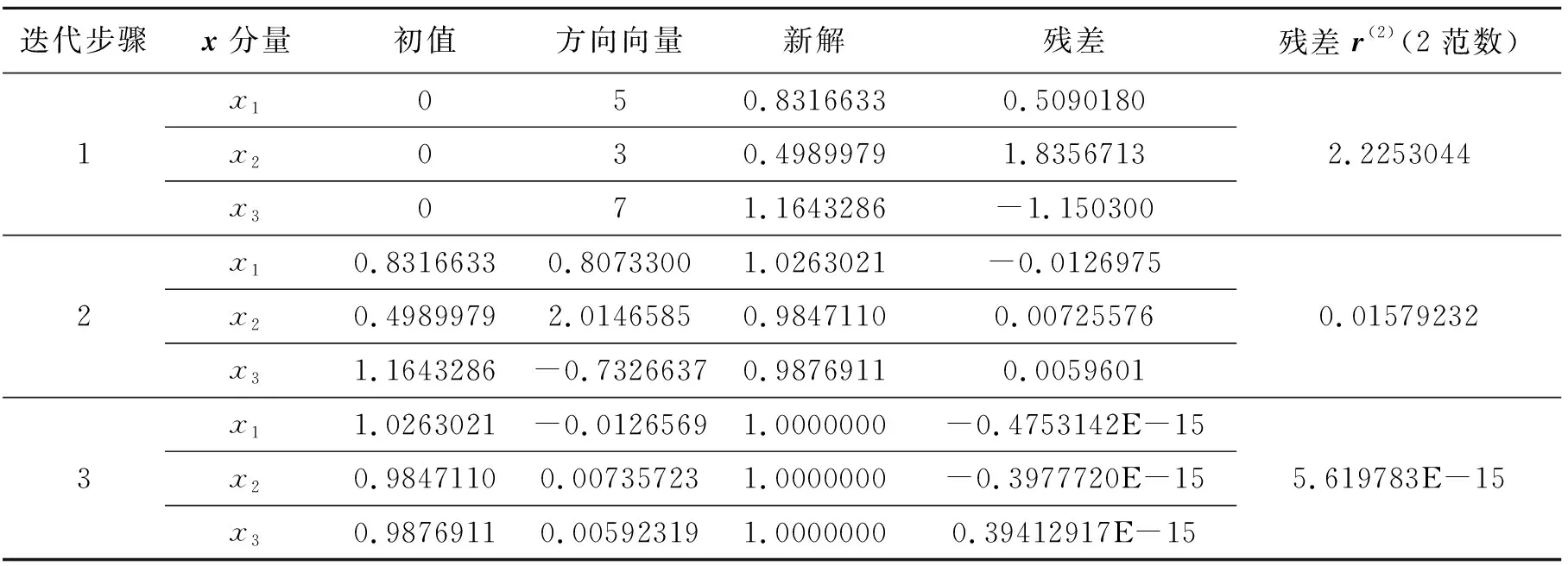
表2 3阶方程迭代情况

这里选的初值为x=(0，0，0)T，该问题的真解为x=(1，1，1)T.所以在四舍五入范围内，共轭梯度法也只需要3步得到非常准确的结果.表3是不同初值对求解过程的影响.

表3 不同初值对应的共轭向量

从上表3可以看出，选取不同的初值，只需经过3次迭代后都可以得到理想的结果，且共轭梯度法确实保持的前后向量的共轭性(在矩阵乘法意义下的正交).

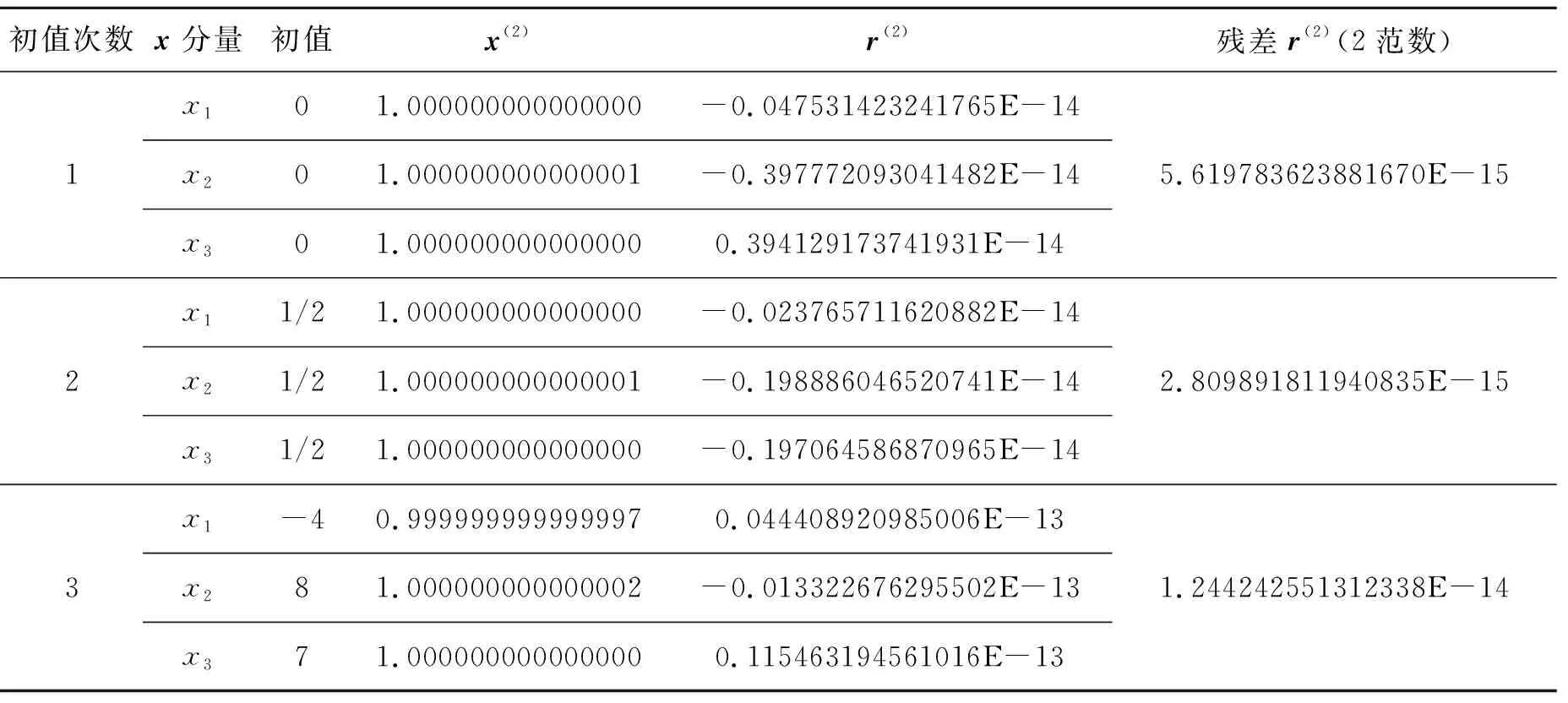
表4 不同初值对应的求解精度

不同的初值，经过3次迭代后的残差向量和解的绝对误差都很小，所以都能得到精度很高的解而且计算稳定.

例3利用共轭梯度法求AX=b的解， 其中

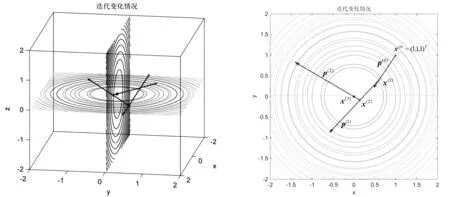
图7 三元模函数共轭梯度法搜索路径

图7分别从三维和二维角度展现对于3阶线性方程，当初值选为x(0)=(1，1，1)T时，共轭梯度法的搜索向量是如何变化的.它能从几何上地展现正交性以及近似解到达最小值点的变化过程——这样就便于学生理解共轭梯度法.

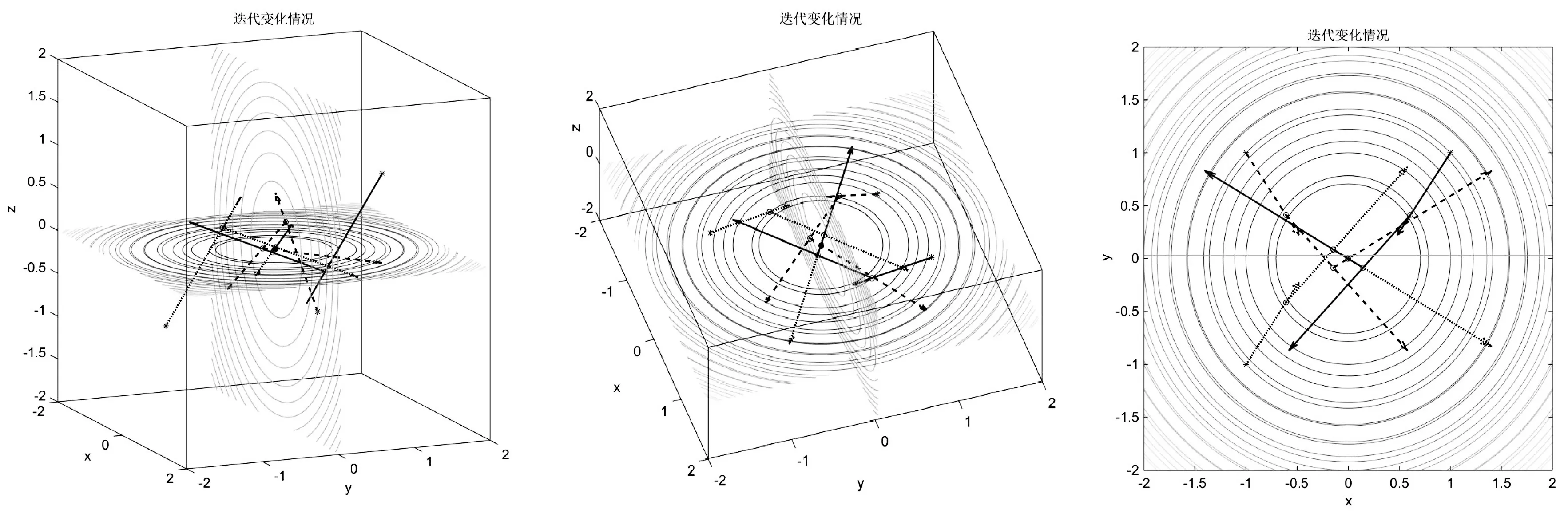
图8 不同初值对三元模函数共轭梯度法搜索路径的影响

图8分别从三维和二维的几个不同角度展现3个初值：x(0)=(1，1，1)T，x(0)=(-1，1，-1)T，x(0)=(-1，-1，-1)T，对于3阶线性方程的搜索向量和在近似解到达最小值点的变化过程.从这里可以看出，不同的初值搜索方向系不一样.当然，这是容易理解的，不同的初值残差自然不同，这导致紧随其后的搜索方向也不同.此外，这个例子也展示了该算法的稳定性——对初值不敏感.

4.4 高维推广

图9是高维空间堆积示意图.虽然下面这种构成很简单，但它向我们展现了高维空间的一种直观构成形式，这种形式类似于直角坐标系(标准正交)的叠加构成.从这个示意图，可以大致理解抽象的高维空间的构成形式及体会共轭梯度法在其中的变化过程.

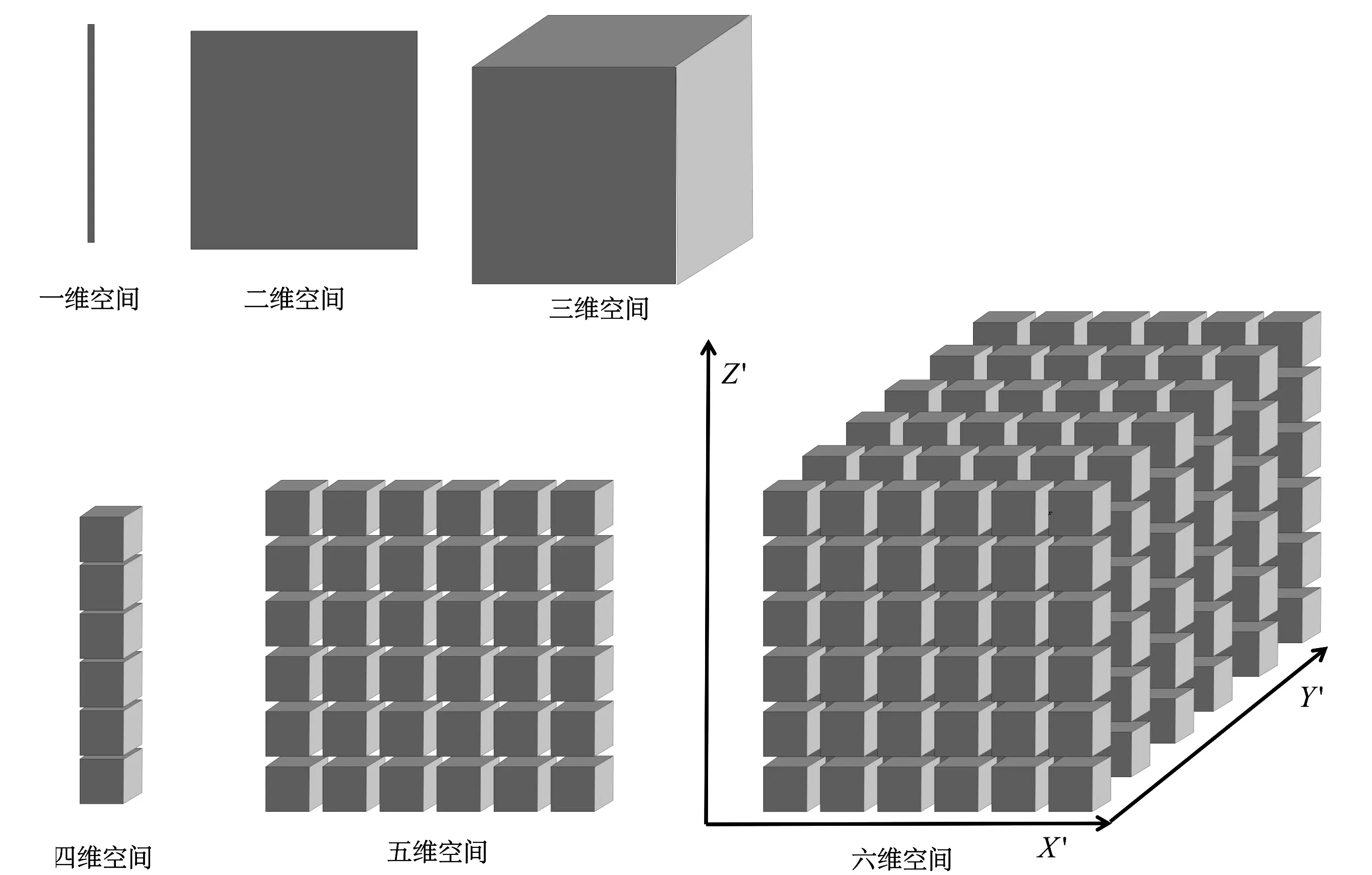
图9 1至6维空间构成示意图

这样一来，高维空间的共轭梯度法，就可以比较容易理解了.比如对含5个自变量线性方程组，其对应的的5元模函数为6维空间(由三位空间叠加而成)的一个超曲面.那么为求其在该空间的极小值(方程组的解)，可以直观地理解为：首先将6维空间的超曲面投影到5维空间中——沿着6维空间的竖直方向(Z′方向)进行投影，并在该5维超曲面上取一个初值，x(0)∈5；然后再沿着斜向方向(Y′方向)求一次最小值，得x(1)∈5，再沿着横向方向(X′方向)求最小值x(2)∈5.这样两次迭代以后，最小值将落入普通的三维空间曲面(值还是5维的)，这样就可以利用继续前面三维空间的图示来理解了.

利用类似的思想可以继续构造或理解7维、8维、9维的空间的共轭梯度法，它们可以3的倍数进行跃迁.这似乎和我们传统文化的“三生万物”有异曲同工之效，所以先贤们确实具有非凡智慧和想象力.由于这种共轭梯度采取空间投影来实现降维的目的，共轭梯度法有时候也被归入投影法，或子空间方法的范畴.

值得说明的是，当然可以采取仿射变换、非线性坐标变换的形式去构造非线性、非正交的空间叠加形式，只不过这种构成比较复杂，这里就不展示了.

5 结 论

和其他学科自然学科一样，如果能把数学方法和结果作为一种可以直接观察的现象时，所产生的进步是非常显著的，这也能让抽象的数学概念或方法成为一个有意思，容易被理解、接受的的成果.怀这样的愿望，从二维问题出发，讨论了共轭梯度法的几何意义和实现：首先通过图形进行直观分析，然后再进行数学推导，从而比较直观地导出了共轭梯度法.通过比较丰富的数值例子和在不同空间中的推广，本文比较好地解释了共轭梯度法的基本思想和计算过程.近两年的教学实践也表明，这样的教学设计，比起传统纯代数分析的教学过程，学生更容易理解，也更能体会到该方法的好处.尤其是在理解诸如“投影”“正则化”这些在数学和工程应用中非常重要，但又很抽象概念和方法的基本思想时至关重要，这也能让学生将这些方法广泛地应用科学研究和工程实践中.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见；感谢学校数学分析课程教学团队在教学交流过程中予以的富有启发意义的建议；感谢《大学数学》编辑予以的耐心指导和细致编撰工作.