基于认知理论的数学概念的教学设计与实践
——以微分概念为例
2022-03-21张冬燕郭从洲
张冬燕, 郭从洲, 刘 倩
(信息工程大学 基础部,郑州450002)
1 引 言
函数的微分是微积分理论中几个重要的核心概念之一,它是构建微分学知识体系的细胞,是领悟微积分思想精髓,实现微积分概念间融合贯通的关键.然而,在实践教学中微分概念一直以来都是学生理解、掌握的难点.文献[1]对浙江某省属重点大学278位同学在学完一元微积分后进行问卷调查,发现55%的同学认为“微分的概念”与中学的内容衔接困难,只有15%位同学能够给予微分准确的定义和描述.从我校课后作业“简述导数与微分概念实质”和“总结:极限、连续、导数与微分概念间的联系与区别,说明理由”的反馈看,仅有9.6%的同学能够建立微分与极限的关系,11.5%的同学理解到微分是函数增量的近似值.而大部分学生对微分概念的掌握停留在微分的计算层面,不能够真正理解并掌握微分是函数增量的近似值这一本质含义.文献[2]调查了这一现象,分析了学生理解微分概念的认知方式并提出“建议以多种表征进行概念教学”.然而,是什么原因造成了微分概念的理解困难?又该如何基于学生的认知方式多表征地进行微分的概念教学呢?下面,笔者尝试从认知心理学的角度分析、揭示学生对微分概念理解困难的原因所在,并基于学习理论采取针对性的策略重构教学设计,促进学生对微分概念的深入理解.
2 微分概念理解困难的原因分析
现代认知心理学告诉我们,在概念学习中学生主要通过两种形式获得概念,分别是概念形成和概念同化[3].概念形成是指学生通过辨别概念的正反例证,在提出、假设、检验中发现概念的本质属性[3].概念同化由美国教育心理学家奥苏伯尔提出,意思是说,学习者头脑中储存了某种认知结构(或知识结构),学习者通过发现新知识与原有认知结构(或知识结构)中的旧知识之间的联系,吸收新知识,把新知识纳入已有认知结构(或知识结构)中,从而使原有认知结构(或知识结构)发生扩大、限制或深化等变化[3].奥苏伯尔对这一学习方式做了一个形象的比喻.他把新学习的知识比作刚驶进港口的船,把头脑中原有的旧知识比作锚桩,当船靠进岸以后,要把船的锚固定在这个事先设置好的牢固的桩上,即锚桩上,船才能停靠岸边,新知识才能被吸收纳入到原有认知结构(或知识结构)中.这个固定新知识的“锚桩”,是与新知识具有相似性的先有经验(包括生活经验、数学知识、活动经验),我国心理学家称之为“同化固定点”[4].同化固定点对学生学习新知识的影响是巨大的,一个人的头脑中储存的同化知识点越丰富,越稳定,越清晰,对新知识的吸收、同化能力就越强.反之,如果一个人头脑中与新知识相关的先有经验(包括生活经验、数学知识、活动经验)也即同化固定点缺乏,模糊不清,那么他同化吸收新知识、新概念的能力就弱.
概念形成和概念同化是学生概念学习中获得概念的主要方式,它们相辅相成,根据认知结构(或知识结构)的复杂程度灵活转换.当学生的认知结构(或知识结构)复杂,先有经验较丰富时,概念同化的学习方式占据主要,当认知结构(或知识结构)单一,先有经验空白、缺乏时,学习方式倾向于概念形成.而无论是概念形成还是概念同化,学生头脑中存储的与新知识相关的先有经验(包括生活经验、数学知识、活动经验)是实现知识吸收、同化的先决条件.
分析学生对微分概念的学习过程,由于高中课程重点介绍极限和导数,未涉及微分相关知识,而导数的定义与微分的定义在形式上相差千里,如果教师在教学时仅以导数概念为学习微分的固化知识点,就会造成学生学习微分时与微分概念相似相近的知识经验缺乏,同化新概念的准备不足而出现学习微分概念时感到陌生,接收困难.事实上,国内绝大部分教材以Δy=AΔx+o(x)的形式定义微分,从概念的表征看,定义中紧密关联的是函数的增量、高阶无穷小概念,和以主部代替全部的“抓大舍小”的近似代替思想.因此要理解微分的定义,必须先掌握函数的增量和高阶无穷小概念,而要领悟微分概念的本质含义,还需要有“抓大舍小”的近似代替思想.也就是说,函数的增量、高阶无穷小概念和近似的思想是学生吸收微分概念的“同化固定点”.函数的增量容易理解,教材强调的不多,是很容易掌握却也极容易被忽视的概念.而高阶无穷小对学生而言,也是一个崭新的初学概念,它在学习微分概念之前一章中学习,有的学生对它还没有形成概念意向,有的对它的理解止于“无穷小”,大部分学生还不能理解高阶无穷小“较快地趋于零”这一性质,也没有高阶无穷小因此可以被“舍弃”做近似计算的思想.这些认知盲点如同一道道屏障影响着学生对微分是函数增量的近似值的深刻认知.因此,可以说,在微分概念的学习过程中,学生对高阶无穷小概念的理解不透彻,对高阶无穷小所隐含的近似代替思想的缺乏是导致微分概念理解困难的链式反应.
3 构建概念形成与概念同化相结合的“混合式”概念教学模式
根据认知心理学理论,学生的认知结构处于不断的发展变化过程中.当学习者的认知结构比较简单,知识经验比较贫乏,作为“固定点”的先有知识不具备或很少,不足以支撑新概念的同化时,学习者将采取概念形成的方式来学习新概念.当学习者的知识结构牢固、系统、丰富,知识经验充足时概念同化的学习方式将成为主要的概念获得方式.为此,针对学生微分概念理解困难的原因,构建如下概念形成和概念同化相结合的“混合式”概念教学模式.

图1 “混合式”概念教学模式
阶段1:针对新概念的“固定点”知识缺乏,设计先行组织者,为学生提供学习新概念所必需的“固定点”知识;
阶段2:尊重学生的认知规律,采用概念形成模式组织教学,引入具体例子,设计概念性例题引导学生发现概念的本质属性,形成概念;
阶段3:利用概念同化学习原理,通过比较新旧概念之间的异同,揭示概念内涵,明辨概念外延,充分利用已有知识同化新概念的理解与吸收.
4 微分概念的教学设计
在此模式下进行微分概念的教学设计,具体教学流程如下:.
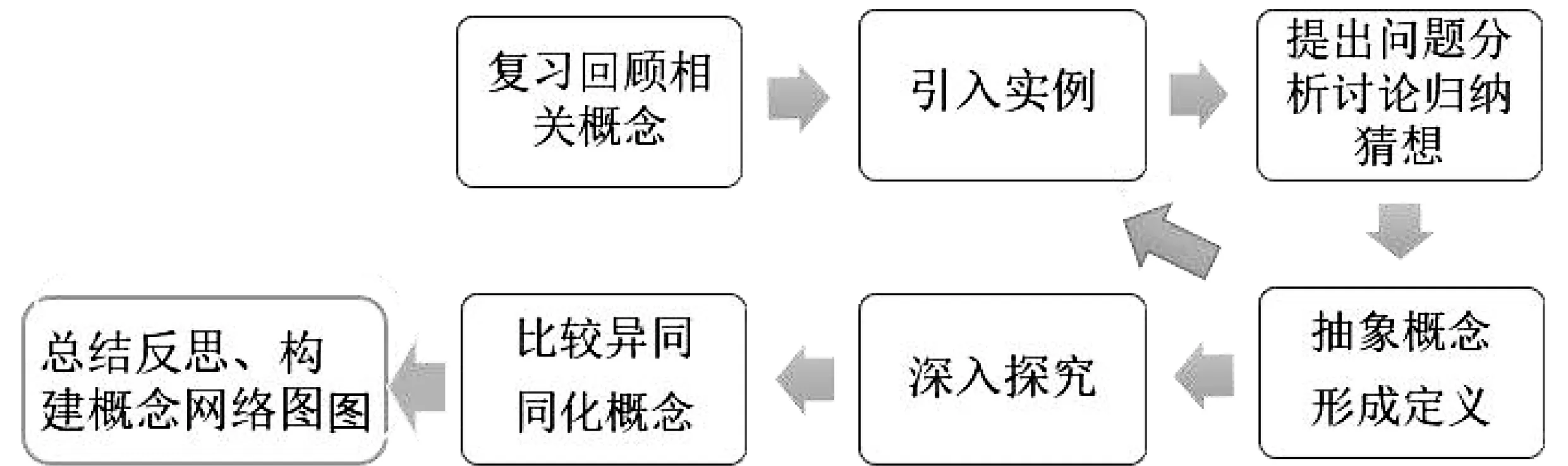
图2 微分概念的教学设计
4.1 以高阶无穷小概念和等价无穷小概念的复习为先行组织者
在学习微分之前,复习回顾高阶无穷小和等价无穷小的概念.如果两个无穷小α(x)与β(x)的商的极限是1,就称α(x)与β(x)为等价无穷小.等价无穷小α(x)与β(x)是否相等呢?不是,是指它们近似相等.为什么说它们近似相等呢?对此问题的剖析中,强调高阶无穷小“较快的趋于零”以至可以被“舍掉”的性质,突出近似代替思想.
4.2 引入实例,复习函数增量概念,为增量近似计算问题的提出埋下伏笔
例1设正方形的边长为x0,面积为y,当边长由x0增加到x0+Δx时,面积增加了多少?
例2给一个边长为r0的立方体的表面涂上厚度为Δr的油漆,需用多少体积的油漆?
例3有一座钟,原摆长0.1m,到了冬季摆长因热胀冷缩短了0.0023m,问这只钟表每分钟快了多少?
4.3 提出问题,分析实例,归纳猜想,抽象出微分定义
从以上例题可以看出,随着函数复杂程度的增加,函数增量的计算越来越复杂,可否退而求其次,对函数的增量作简化的近似计算?
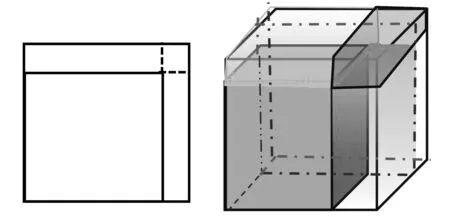
图3 图4
4.4 深入探究可微的条件和微分的计算,利用导数知识同化微分概念
定理函数f(x)在点x0可微等价于f(x)在点x0可导,且A=f′(x0)或dy=f′(x0)Δx.
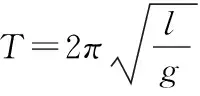
函数在l0=0.1处微分
4.5 比较异同,同中见异,利用同化策略完成微分概念深化、延伸

图5
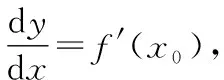
4.5.1 从几何图形上作对比.
导数刻画的是函数的变化率,而微分反映的是函数改变量的估值.从几何上看,Δy-dy=o(Δx),PN=o(Δx),当|Δx|很小时,|Δy-dy|=|PN|更小,因此当|Δx|=|x-x0|很小时,曲线y=f(x)与它在点M的切线近乎重合,“曲线”可视为“直线”.
4.5.2 从应用上作对比.
导数用于解决变化率问题,而微分作为函数增量的局部近似值,常用于近似计算.将近似式Δy≈dy展开,即有
f(x)≈f(x0)+f′(x0)(x-x0).
(*)
(*)式右边是线性函数,所以在代数上,(*)式表示在微小局部用线性函数近似代替非线性函数,即非线性函数的局部线性化.“局部线性化”是微积分的基本思想,利用微积分处理实际问题时,通常将“不均匀”的视为“均匀的”,将“非线性的”视为“线性的”[5],如此等等,使原本复杂的问题大大简化.如例3,虽然无法得到钟表的每分钟快了的精准时间,但是却可以简单地估算钟表每分钟快的大致时间.事实上,用dT≈ΔT得
因此钟表每分钟大约快了0.437s.当然,用dT近似代替ΔT的近似程度如何?近似误差是多少呢?这些问题我们将在后面继续研究.
4.6 指导总结反思,构建概念网络图,培养元认知能力
以问题的形式指导学生回顾总结微分概念的学习,引导学生反思、审视自己的认知过程,促进学生元认知能力的发展.
(i) 这节课学习的主要内容是什么?什么叫可微?什么是微分?对微分的概念是否理解并记住了?可以说出你对微分概念的理解吗?
(ii) 与微分概念相关的知识点是什么?你能列出或画出它与其他知识点之间的联系吗?你能分辨出微分与其他知识点的区别吗?和学生共同构建与微分概念相关的知识点之间的网络结构图;
(iii) 在这节课的学习中有不清楚、没有理解的地方吗?有经思考仍没有明白的问题吗[6]?
4.7 教学效果
按照以上教学设计开展微分概念的教学,与往届学生相比,从历年的课后作业来看,在作业“简述导数与微分概念实质”和“总结:极限、连续、导数与微分概念间的联系与区别,说明理由”的简答中,能够从几何和近似计算角度理解性的描述微分定义的人次大幅提升,具体结果见表1.
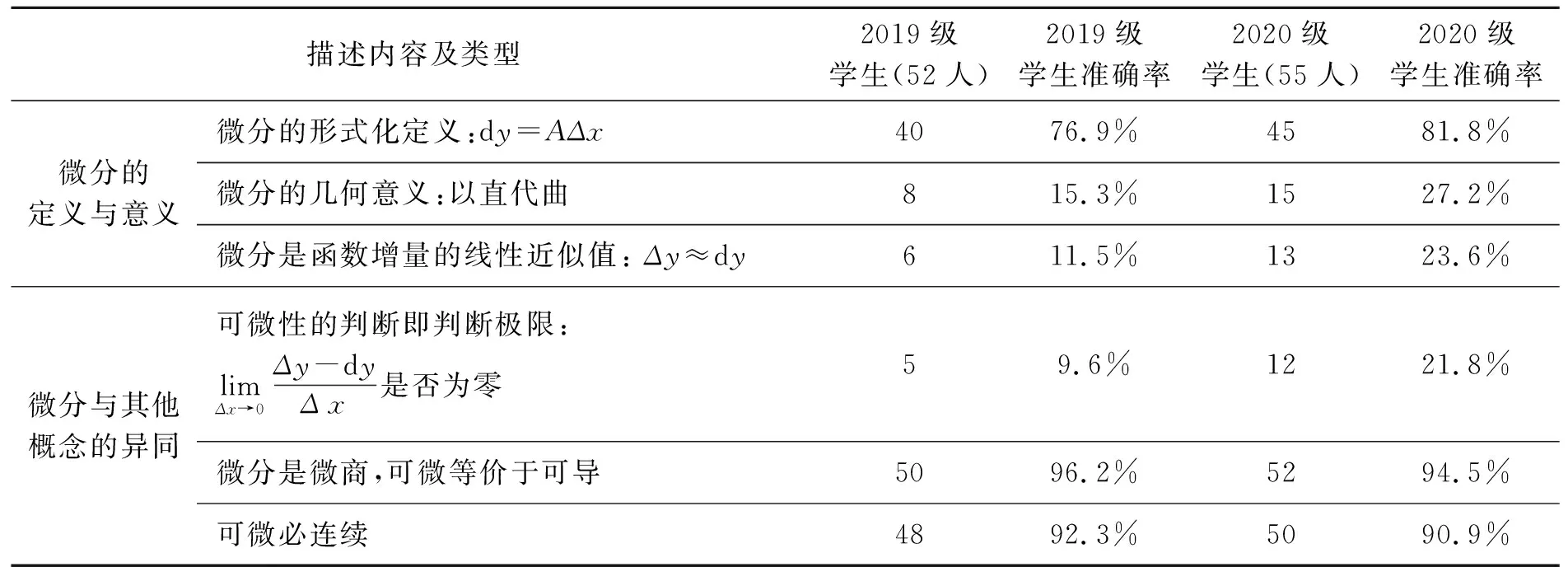
表1 对微分概念的理解作答情况
从表格的统计数据可见,本届教学班学生所获得的微分概念意象与微分定义原型的吻合度增加,学生对微分概念的认知有所加深,“混合”了概念形成和概念同化两种概念吸收方式的微分概念的教学有效促进了学生对微分概念的理解.
5 结 论
数学概念是学生在学习数学中赖以思维的基础.2004年喻平教授提出了数学概念教学的三种模式:概念形成模式,概念同化模式和问题引申模式[7].然而“概念形成和概念同化不是相互独立的,概念形成包含着同化因素,概念同化也含有概念形成因素.因此在概念教学中,应当把两种方式结合起来…”[8]正是基于这样的思考,本文首次构建了融合概念形成和概念同构两种概念获得方式的数学概念教学模式,并在此模式下开展了微分概念的教学实践.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
