事件创设稳中求新 概率求解活而不难
2022-03-21邓艳花陈远刚
邓艳花 陈远刚

摘 要:针对“事件的概率”这一专题,分析全国各地中考数学试卷,发现试题关注学生“双基”,聚焦学生提取、分析及处理数据能力的特点,具有突出数学文化育人的价值取向. 试题设计贴近生活,考查学生的数学建模素养,结合统计初步知识进一步考查学生的数据分析素养. 文章分析各地中考数学试题,为本专题中考备考提供建议.
关键词:中考试题;事件的概率;试题赏析;备考建议
根据教育部2014年《关于全面深化课程改革落实立德树人根本任务的意见》,在中考数学试题的设计上,全国各地更多地注重考查课堂教学是否落实培养、发展学生的核心素养.“统计与概率”是《义务教育数学课程标准(2011年版)》(以下简称《标准》)的四大板块之一,“事件的概率”在考查上更关注学生的数学建模及数据分析素养.
一、2021年中考数学“事件的概率”试题分布一览表
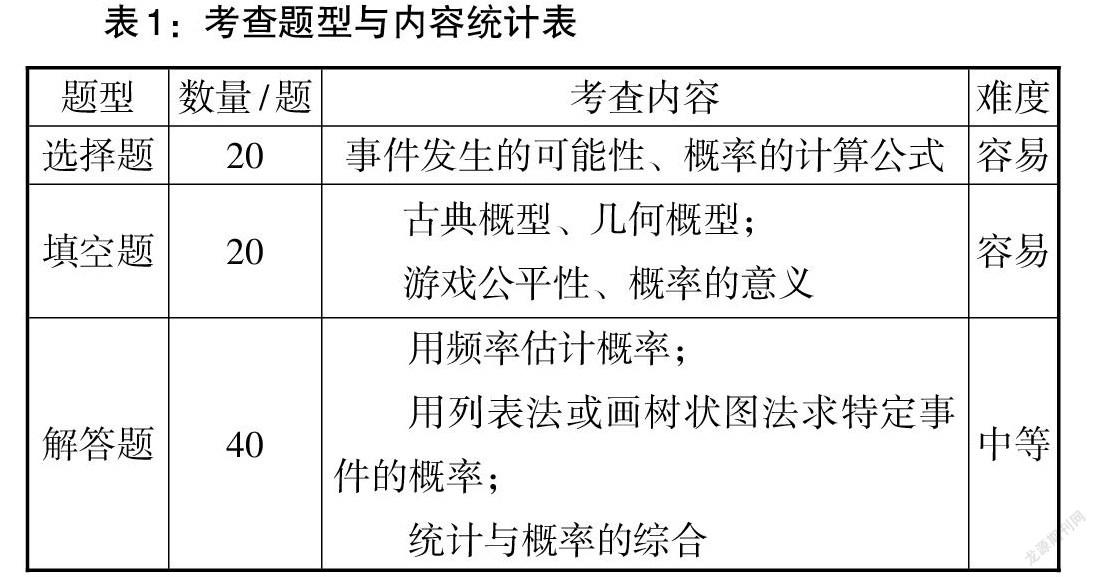
分类统计2021年全国各地中考数学试卷,涉及“事件的概率”的试题共有80道题,题量设计以1道题居多,题型与内容具体情况如表1所示.
由表1可知,试题的考查题型以解答题为主,选择题、填空题为辅.考查内容主要是:判断事件发生的可能性;会计算简单事件发生的概率;根据题设情境,能抽象概括出概率模型,从而准确利用列表法或画树状图法计算事件的概率;能综合运用统计学知识进行数据分析.
二、试题特点分析
1. 在实际情境中考查学生对基础知识的理解和对基本技能的掌握
(1)对基础知识的理解.
与中考数学中“数与代数”“图形与几何”的考查难度相比,“事件的概率”考查难度较低,着重考查学生对基本概念、基础知识的简单运用,得分率较高.
例1 (湖北·武汉卷)下列事件中是必然事件的是( ).
(A)抛掷一枚质地均匀的硬币,正面朝上
(B)随意翻到一本书的某页,这一页的页码是偶数
(C)打开电视机,正在播放广告
(D)从两个班级中任选三名学生,至少有两名学生来自同一个班级
例2 (浙江·湖州卷)下列事件中,属于不可能事件的是( ).
(A)经过红绿灯路口,遇到绿灯
(B)射击运动员射击一次,命中靶心
(C)班里的两名同学,他们的生日是同一天
(D)从一个只装有白球和红球的袋中摸球,摸出黄球
【评析】例1、例2考查必然事件、不可能事件、不确定事件的概念:一定会发生的事件叫做必然事件;一定不会发生的事件叫做不可能事件;不确定是否会发生的事件叫做不确定事件,亦叫做随机事件.
在学习的过程中,需要通过观察生活中的客观规律、数学事实和自然现象等(如抛出的篮球会落回地面、掷出两枚骰子的点数之和大于1、日出东方等)来理解必然事件. 通过判断是否违背客观规律事实(如两个正数的和为负数、水中捞月、日出西方等)来理解不可能事件. 通过明天下雨、过马路遇到红灯、打开电视机正在播放新闻等来理解什么是可能发生的事件,什么是可能不发生的事件. 而这些有可能发生也有可能不发生的事件就叫做随机事件. 在学习的时候,一定要清楚事件分类的原则,切忌生搬硬套.
(2)对基本技能的掌握.
例3 (湖南·岳阳卷)一个不透明的袋子中装有5个小球,其中3个白球,2个黑球,这些小球除颜色外无其他差别,从袋子中随机摸出1个小球,则摸出的小球是白球的概率为 .
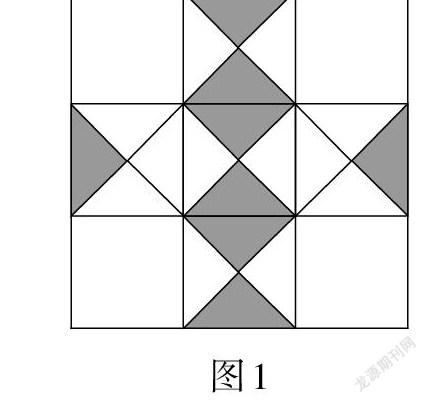
例4 (江苏·苏州卷)一个小球在如图1所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
【评析】例3可以通过直接列举法,利用简单事件的概率计算公式[PA=mn]求解出正确答案.学生一定要掌握簡单随机事件的概率的计算公式:如果一个事件的发生有n种可能,且这些可能的发生几率都是相同的,其中事件之一(记为A)出现的数量为m,那么事件A出现的概率[PA=mn]. 理解公式的本质,避免因为对公式的不清晰导致数据用错而失分. 例4则是以几何图形为载体,考查“命中率”的概率问题,也称几何概型. 求解几何概型题的方法:先求题目提供的几何图形的面积S(或体积V),再求事件A发生的目标区域的面积[S](或体积[V]),则[PA=SVSV].
考查简单随机事件概率的计算类试题难度较低,设计的实际情境往往都是教材延伸而来的摸取、转盘等事件,与学生的认知发展水平高度契合. 对应的概率模型集中于单次重复试验或几何概型. 通过直接列举法,正确运用概率的计算公式,即可完成解答. 学生在学习时,要懂得数学来源于生活,数学就存在于我们身边,学会用数学眼光观察生活中的“事件的概率”. 除了能用公式计算事件的概率,还应注重逐渐使自己具备将实际情境转化为数学模型的能力.
2. 在生活情境中考查能运用列表法、画树状图法求事件的概率
例5 (江苏·南京卷)不透明的袋子中装有2个红球、1个白球,这些球除颜色外无其他差别.
(1)从袋子中随机摸出1个球,放回并摇匀,再随机摸出1个球. 求两次摸出的球都是红球的概率.
(2)从袋子中随机摸出1个球,如果是红球,不放回再随机摸出1个球;如果是白球,放回并摇匀,再随机摸出1个球. 两次摸出的球都是白球的概率是
.
分析:第(1)小题是有放回的重复试验,每1个球被摸出来都是等可能的. 这种情况下,如果直接运用列举法,易出现事件结果总数重复或遗漏,建议使用列表法或树状图法来进行事件的整理、分析、计算,最后获得准确的结论.
第(2)小题涉及分类讨论:如果摸出红球则进行不放回的重复试验;如果摸出白球,则进行有放回的重复试验. 需要注意的是,此时并不是等可能事件,所以不能用树状图或列表法直接解题,选用概率分步原理解题即可.
解:(1)畫树状图如图2所示.
所以共有9种等可能的结果.
而两次摸出的球都是红球的结果为4次,
所以两次摸出的球都是红球的概率为[49].
(2)第一次拿出红球的概率为[23].
不放回,再拿出白球的概率为[12].
第一次拿出白球的概率为[13].
放回后,再拿出白球的概率为[13].
故两次摸出的球都是白球的概率是[0+13×13=19].
故填[19].
例6 (江苏·苏州卷)4张相同的卡片上分别写有数字0,1,-2,3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上数字是负数的概率为
;
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜. 小敏设计的游戏规则公平吗?为什么?(试用树状图或列表等方法说明理由.)
分析:此题设计的是游戏公平性问题. 值得注意的是,游戏是否公平并不是胜、负事件发生的概率均为二分之一,而是彼此之间概率相等则公平,否则不公平.
第(1)小题由于只进行了一次试验,所以可以运用直接列举法,利用概率的计算公式即可求出正确答案.
第(2)小题在两次试验中加入有理数的减法和不等式的知识,题目中已明确要求用树状图或列表等方法计算游戏规则下事件发生的概率.
解:(1)共有4种等可能的结果,其中数字是负数的情况占1种.
P(数字是负数) =[14].
(2)用树状图(如图3)列出所有等可能的结果.
因为共有12种等可能的结果,两个数的差为非负数的情况有6种,
所以P(结果为非负数)[=612=12],
P(结果为负数)[=612=12].
所以游戏规则公平.
在画树状图或列表时,要注意所列举的情况不重复、不遗漏,在平时积累学习经验时,就要有意识地总结画树状图或列表时所遵循的原则:从上到下,从左到右,不重不漏.
“事件的概率”使数学具有了更浓厚的生活气息,揭示了数学的生活属性. 学生备考时要注重数学与其他学科的融会贯通:读题、审题时需要结合其他学科的解题特点找关键词、关联词、时间顺序等,厘清事件发生的条件与先后顺序,挖掘隐含条件,从而准确将文字材料转化为数学模型.
3. 在数学知识背景下进行知识转化
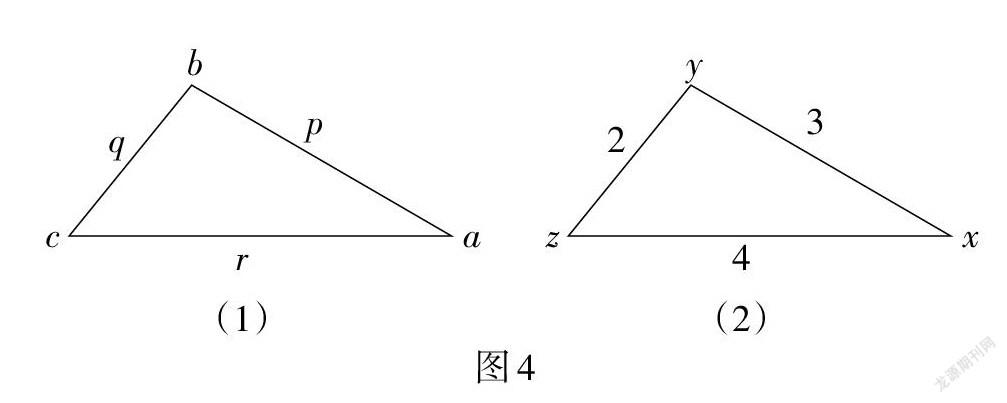
例7 (四川·成都卷)我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和. 如图4(1),[ar+cq+bp]是该三角形的顺序旋转和,[ap+bq+cr]是该三角形的逆序旋转和. 已知某三角形的特征值如图4(2)所示,若从1,2,3中任取一个数作为x,从1,2,3,4中任取一个数作为y,则对任意正整数k,此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是________.
【评析】此题命题载体是三角形,考查自定义情境下概率的计算. 考点1:不等式的性质——不等式的两边同时加(减)同一个数(式子),不等号的方向不变. 考点2:在数量有限的等可能事件中,用列表法或画树状图法将事件所有可能发生的结果描述出来,用概率计算公式求目标事件的概率. 基于对数学知识的理解,将数学事实抽象概括出对应的数学概率模型,这既是解题的关键,也是容易出现错误的地方. 如果对题目背景的数学知识掌握不清,甚至对数学事实认知错误,那么无法正确求解就是一个必然事件了. 数学世界里的每一个知识点都并非独立存在,在学习的过程中,要有大局观,能进行知识间的转化. 此题的解题思路是:先画树状图或列表确定x,y的所有等可能的结果数,分别计算符合要求的结果数,再利用概率公式计算即可得到答案.
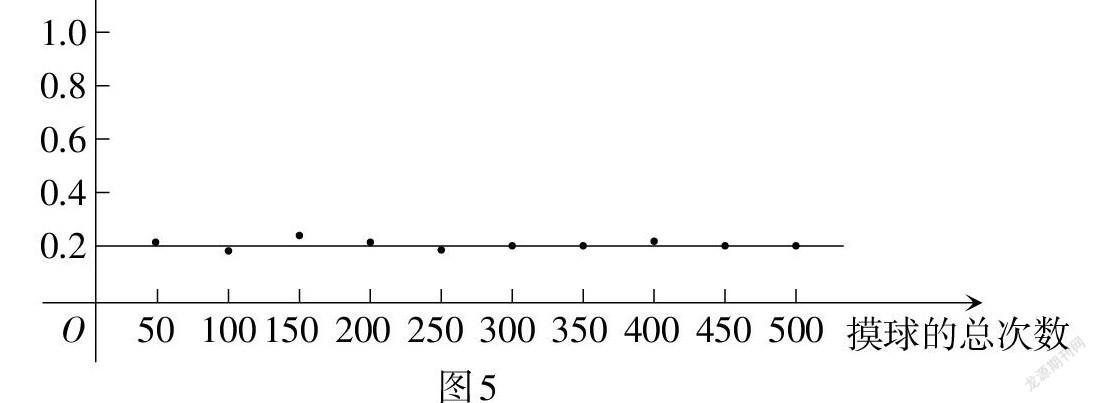
例8 (湖北·宜昌卷)社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里装有几十个除颜色不同外其余均相同的黑、白两种球,将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程. 整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系的图象(如图5),经分析可以推断盒子里个数比较多的是
(填“黑球”或“白球”).
【评析】计算事件的概率,除了运用概率公式外,还能用频率来进行估计,前提条件是进行了大量的重复试验:当试验重复的次数不断增加时,频率会稳定在某一个数值附近,此时可以用事件的频率估计事件发生的概率. 例如,此题由图5可知,摸出黑球的频率稳定在0.2附近,所以摸一次摸到黑球的概率为0.2,因此推断盒子里个数较多的是白球.
4. 与数据的统计进行“捆绑”考查
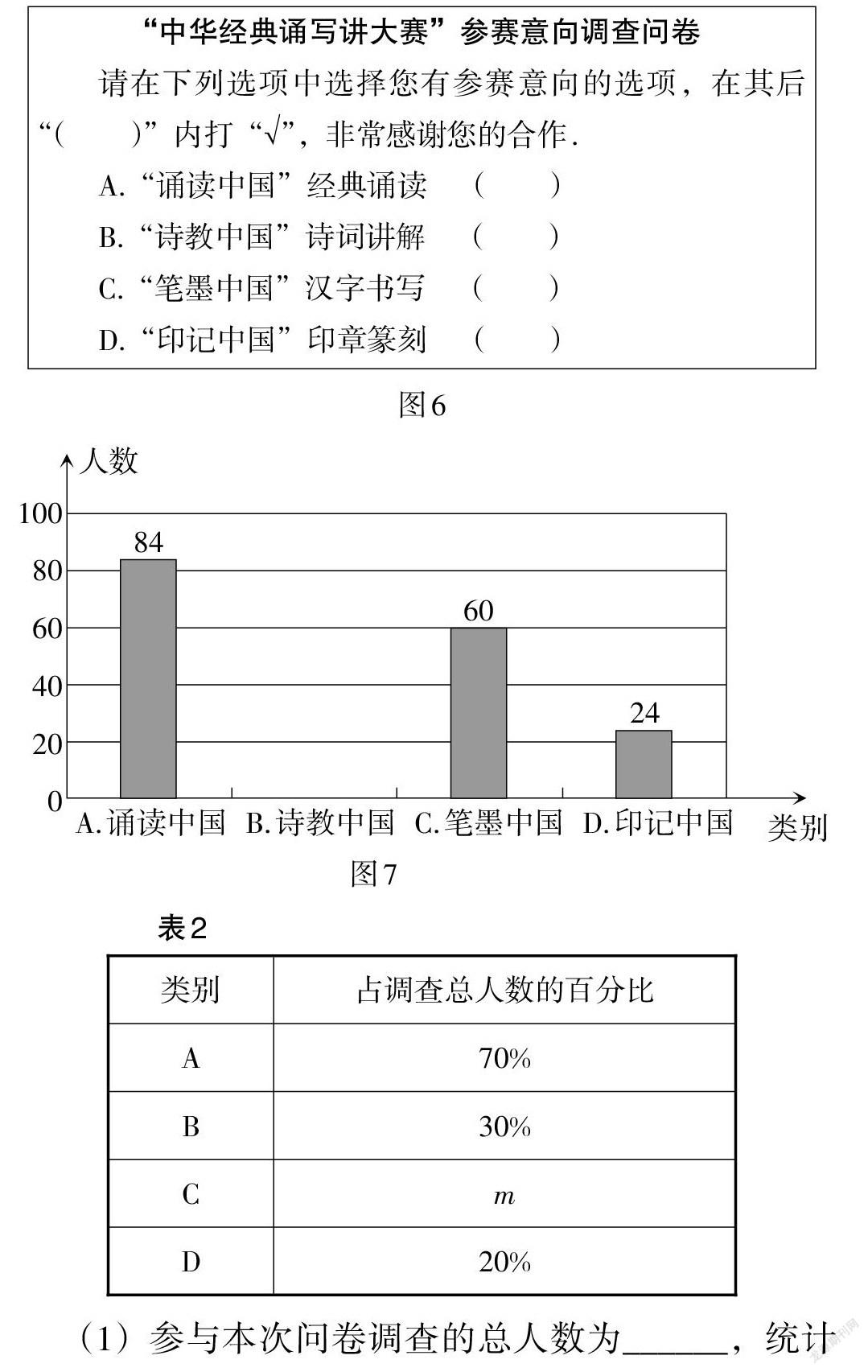
例9 (山西卷)近日,教育部印发了《关于举办第三届中华经典诵写讲大赛的通知》,本届大赛以“传承中华经典,庆祝建党百年”为主题,分为“诵读中国”经典通读,“诗教中国”诗词讲解,“笔墨中国”汉字书写,“印记中国”印章篆刻比赛四类(依次记为A,B,C,D). 为了解同学们参与这四类比赛的意向,某校学生会从有意向参与比赛的学生中随机抽取若干名学生进行问卷调查(调查问卷如图6所示),所有问卷全部收回,并将调查结果绘制成如图7所示的统计图和如表2所示的统计表(均不完整). 试根据图表提供的信息,解答下列问题.
[“中华经典诵写讲大赛”参赛意向调查问卷
请在下列选项中选择您有参赛意向的选项,在其后“( )”内打“√”,非常感谢您的合作.
A.“诵读中国”经典诵读 ( )
B.“诗教中国”诗词讲解 ( )
C.“笔墨中国”汉字书写 ( )
D.“印记中国”印章篆刻 ( )
(1)参与本次问卷调查的总人数为______,统计表中C的百分比[m]为_____.
(2)补全统计图.
(3)小华想用扇形统计图反映有意向参与各类比赛的人数占被调查总人数的百分比,是否可行?若可行,求出表示C类比赛的扇形圆心角的度数;若不可行,试说明理由.
(4)学校“诗教中国”诗词讲解大赛初赛的规则是:组委会提供“春”“夏”“秋”“冬”四组题目(依次记为C,X,Q,D),由电脑随机给每位参赛选手派发一组,选手根据题目要求进行诗词讲解. 试用列表或画树状图的方法求甲、乙两名选手抽到的题目在同一组的概率.
分析:(仅分析第(4)小题)此题考查了统计学与概率学知识的综合应用. 此类题型都先围绕统计学知识设置问题,接着才是设计具体的场景考查学生对概率知识的掌握程度. 此题第(4)小题的解题思路如图8所示.
解:(仅分析第(4)小题)画树状图如图9所示.
列表法如表3所示.
由画树状图(或列表)可知,总共有16种结果,每种结果出现的可能性都相同.
其中甲、乙两名选手抽到的题目在同一组的结果有4种.
所以[P抽到的题目在同一组=416=14].
【评析】例9及其他设计为抽到不同牌面、抽到特定群体的概率等类似问题,其解题思路都如图8所示,根据题意用树状图法或列表法将所有情况不重复、不遗漏地列出来,再用概率公式计算.
5. 关注数学文化的育人功能
例10 (江苏·盐城卷)圆周率π是无限不循环小数. 如图10,历史上,祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究. 目前,超级计算機已计算出π的小数部分超过31.4万亿位. 有学者发现,随着π小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
(1)从π的小数部分随机取出一个数字,估计数字是6的概率为 ;
(2)某校进行校园文化建设,拟从以上4位科学家的画像中随机选用2幅,求其中有1幅是祖冲之的概率(用画树状图或列表方法求解).
【评析】此题以圆周率π为背景,蕴含中外数学家对π的研究历史,寓数学文化于试题中,考查学生应用概率公式及画树状图法或列表法计算事件的概率. 准确把握这个事件中有10种等可能的结果,“数字是6”是其中一种可能性,所以第(1)小题可以通过直接列举,运用概率公式计算得出答案. 第(2)小题是抽取问题,将所有可能发生的结果不重复、不遗漏地一一列举出来,这是用画树状图法或列表法解题的关键.
三、典型解法赏析
以下例11、例12是求解“事件的概率”类型的基本模式.
例11 (甘肃·威武卷)一个不透明的箱子里装有3个红色小球和若干个白色小球,每个小球除颜色外其他完全相同,每次把箱子里的小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量重复试验后,发现摸到红色小球的频率稳定于0.75左右.
(1)试估计箱子里白色小球的个数.
(2)现从该箱子里摸出1个小球,记下颜色后放回箱子里,摇匀后,再摸出1个小球,求两次摸出的小球颜色恰好不同的概率(用画树状图或列表的方法).
考点:有放回的重复试验;用频率估计概率;用画树状图法或列表法计算概率;方程的思想.
分析:此题属于有放回的重复试验的概率问题,每一个事件的发生具有等可能性,考查学生的阅读能力、审题建模能力和数学思维能力,以及对事件进行分析、分解、转化、归纳的能力. 第(1)小题考查了用频率估计概率:当试验次数足够多时,频率会稳定在某个数值附近,这个常数可视为概率. 因此,得到结论:摸到红球的概率为0.75. 接着运用方程的思想,通过概率公式[PA=mn]列方程求解. 第(2)小题仍然是有放回的重复试验,题目设计为两步试验,可以利用列表或画树状图的方法得到所有的等可能的结果数,得到符合条件的结果数,再利用概率公式计算即可得到答案.
解:(1)实际问题抽象概括为数学概率问题.
因为通过多次摸球试验后发现,摸到红球的频率稳定在0.75左右,所以估计摸到红球的概率为0.75.
直接列举目标事件的结果总数,然后运用概率的计算公式即可.
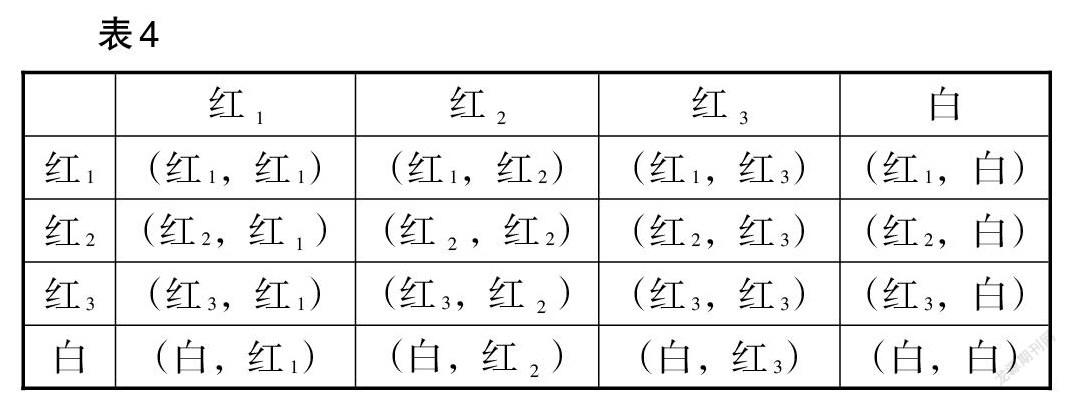
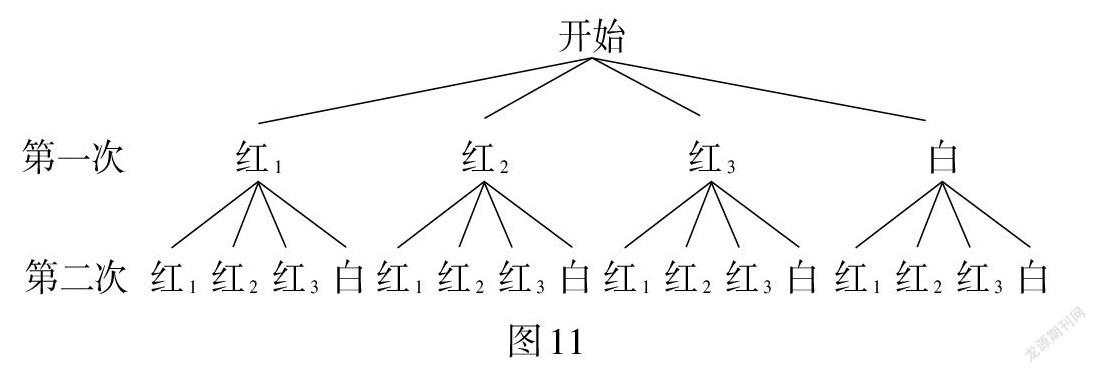
因为一共有16种等可能的结果,
两次摸出的小球颜色恰好不同的有:
(红1,白)(红2,白)(红3,白)(白,红1)(白,红2)(白,红3),共6种.
所以两次摸出的小球恰好颜色不同的概率为[616=38].
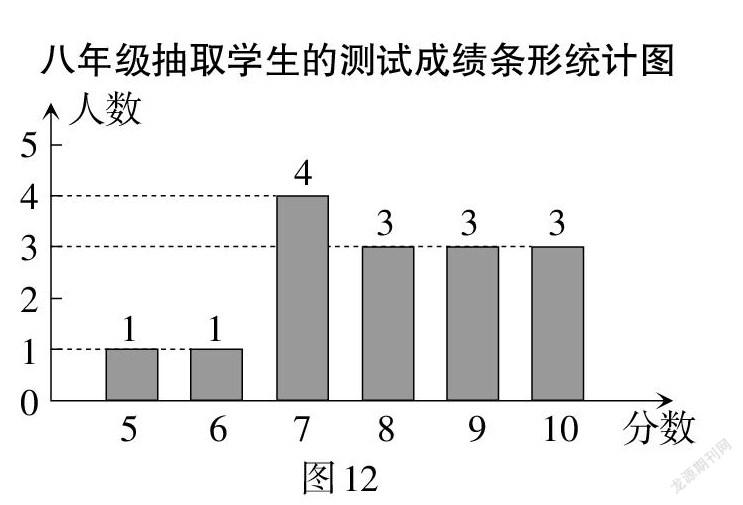
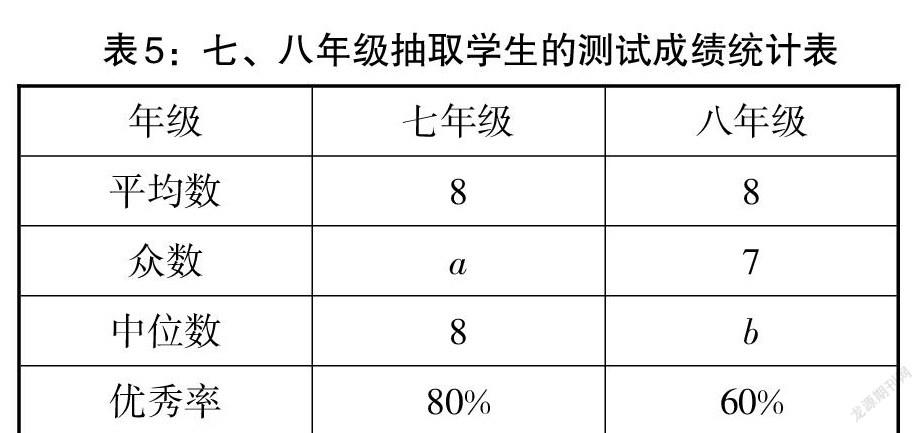
例12 (辽宁·盘锦卷)某校七、八年级各有500名学生,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及以上为优秀),相关数据统计、整理如图12、表5所示. 七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10.
(1)填空:a的值为______,b的值为______.
(2)根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?并说明理由(写出一条即可).
(3)试估计七、八年级学生对党史知识掌握能够达到优秀的总人数.
(4)现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,试用列表法或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.
考点:众数、中位数的定义;平均数、众数、中位数的意义;条形图的读取;数据的代表性(用样本代表总体);画树状图法或列表法计算概率.
分析:(仅分析第(4)小题)由题目已知信息可以获知七年级10分人数有1人,八年级有3人. 从这4人中抽取2人作为代表参加比赛,这是一个不放回的重复试验模型. 因为试验有两次,同时题目要求通过用列表法或画树状图法,利用概率公式计算即可得到解答.
解:(仅求解第(4)小题)实际问题抽象概括为数学概率问题.
10人中抽取2人,属于不放回的重复试验模型.
用列表法或画树状图法将事件发生的结果总数不重不漏地列出.
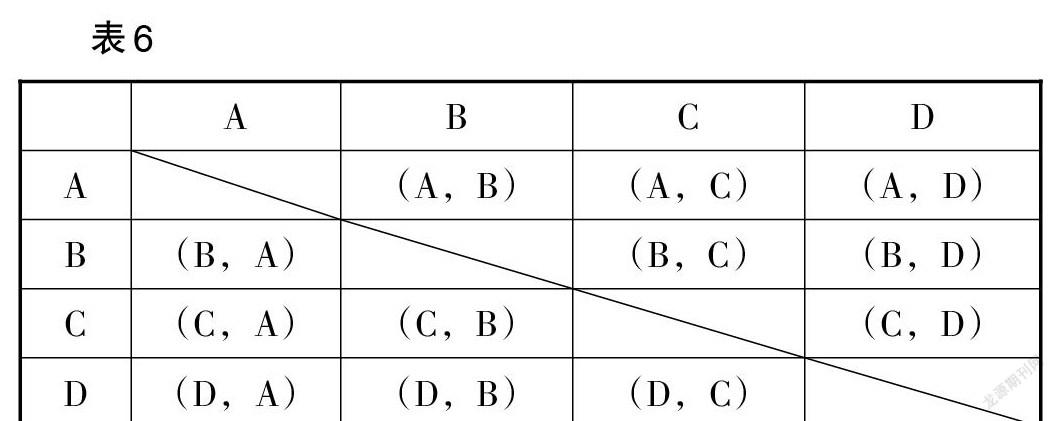
把七年级的学生记作A,八年级的三名学生记作B,C,D,列表如表6所示.
直接列举目标事件的结果总数,然后运用概率的计算公式,可求得.
由表6可知,一共有12种等可能的结果,恰好每个年级都有一个的结果数是6,2人中恰好是七、八年级各1人的概率是[12].
四、备考建议
1. 梳理清楚“事件的概率”的整个知识架构
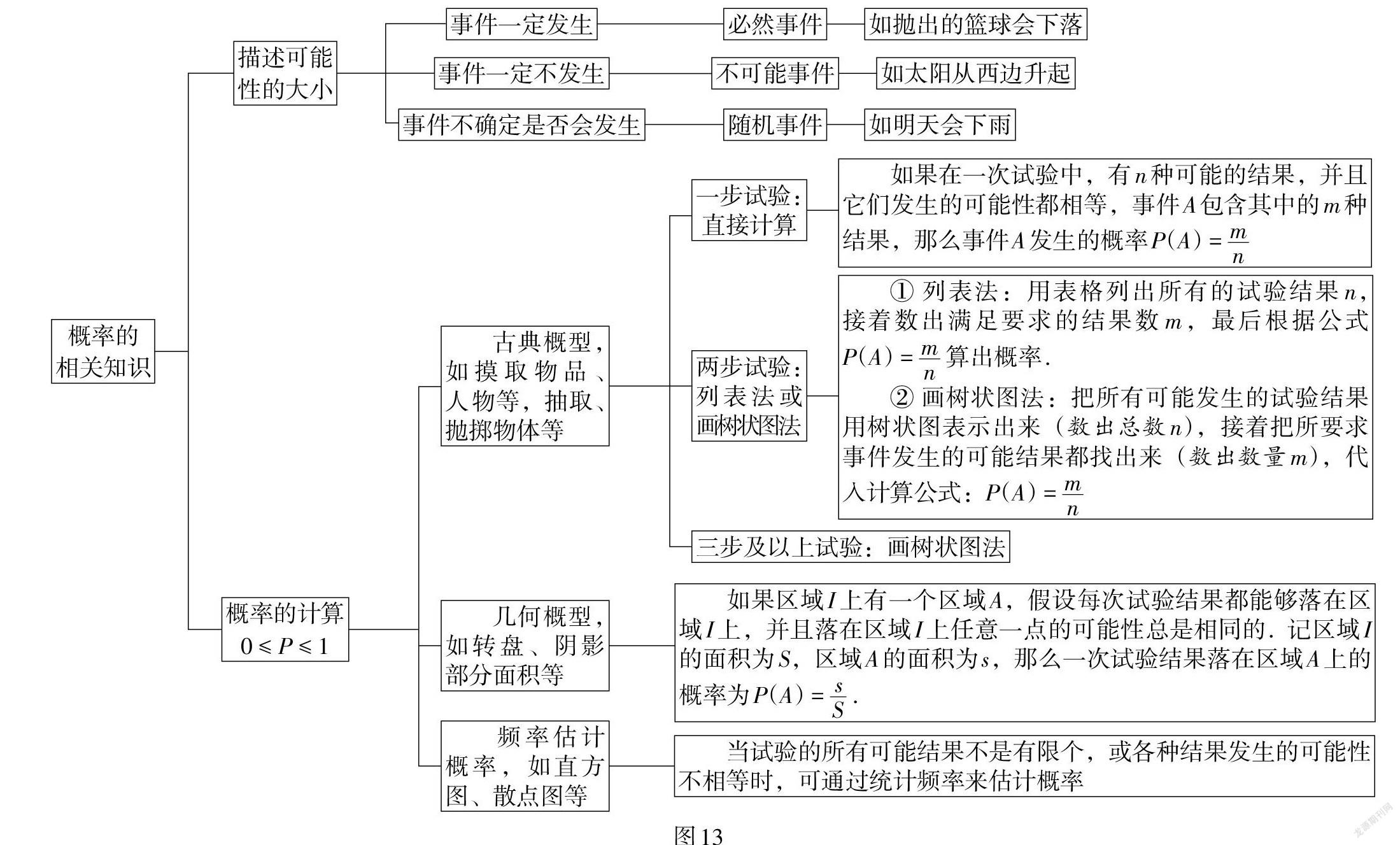
对于《标准》要求的有关概率的概念要了然于胸,能区分不同事件发生的可能性. 能辨析不同的概型,并根据概型特点应用概率的计算公式. 能正确选择列举法、列表法或画树状图法来计算不同事件发生的概率. 有关概念如图13所示.
2. 解要有法
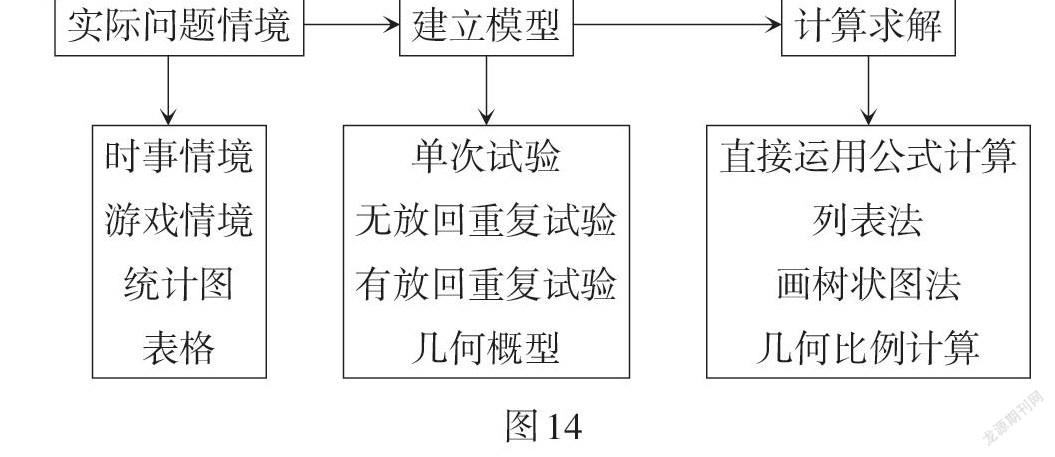
“事件的概率”是中考数学中相对独立的一个知识板块,知识容量比“数与代数”“图形与几何”相对较小,常与统计知识捆绑考查. 命题设计上,多创设不同的生活场景,题材内容广泛,文字信息量大,对学生阅读材料、提取有效信息的能力要求较高. 解决问题的关键是正确地用数学知识描述与分析事件,不仅仅考查学生对知识的应用、数值计算,还有将文字语言转化为数学语言的数学建模思想. 对学生的审题能力有较高的要求:已知什么?要求什么?在题目中提取解答问题所需的关键信息,并做出准确的判断. 解题的基本流程如图14所示.
通过创设实际问题情境,如国家政策、国家大事、游戏或比赛、人员抽取、工作安排等,厘清各组数据之间的关系,确定与之对应的概型,如单次试验的古典概型、有放回或无放回的重复试验模型、几何概型,從而建立基于题目事实的数学模型,最后计算目标事件的概率. 例如,一步试验直接运用概率公式计算;两步试验用列表法或画树状图法;三步及以上试验用画树状图法.
3. 养成“解后反思”的解题习惯
虽然“事件的概率”有着题型变化不大、命题设计贴近生活、建模门槛较低等特点,但是仍然有一部分学生在这个考查环节知识掌握不牢. 这反映出学生对概率意义的理解不清晰,对概率的现实运用存在操作上的困难,学生数学活动经验的积累不到位. 学生在备考时要关注自己平时做题时容易犯错的题型和知识点,如不能清楚界定是单次试验还是无放回的重复试验,用列表法或画树状图法时没能做到不重复、不遗漏地一一列举出来等. 把自己每次做错或解答过程中存疑的问题收集起来,建立“事件的概率”专题反思. 归纳总结出自己没能完全解答的原因:是概念模糊导致的?不能准确辨析事件之间的关系导致计算出错?阅读能力有待提高?文字语言转化为数学语言不准确?在用列举法、画树状图法时没有做到不重复、不遗漏?关注自己解题容易出错的地方,做好错题收集及解题反思,形成行之有效的方法总结,比盲目的“题海战术”要高效得多.
参考文献:
[1]中华人民共和国教育部制定. 义务教育数学课程标准(2011年版)[M]. 北京:北京师范大学出版社,2012.
[2]黄涛,汤曙光,何超林. 2020年中考“事件的概率”专题解题分析[J]. 中国数学教育(初中版),2021(3):32-40.
[3]赵萍. 2020年高考全国Ⅰ卷概率与统计试题分析及备考建议[J]. 中国数学研究(华南师范大学版),2020(9):18-22.
[4]陈远刚. 中小学数学教师的教学自信探究[M]. 广州:华南理工大学出版社,2021.
3547501908208
