立足基础·渗透思想·注重实践·传递文化
2022-03-21黄若明
黄若明






摘 要:2021年中考对“事件的概率”领域的考查延续了近几年试题“稳中求变,变中求新”的特点,重视对事件的概率的基础知识和基本模型的考查,关注能力,注重应用,符合《义务教育数学课程标准(2011年版)》的理念和要求. 现对2021年全国各地中考试卷中关于“事件的概率”领域的试题的考查特点进行分析,总结命题规律,为2022年的中考复习教学提供参考.
关键词:事件的概率;命题分析;复习建议
“事件的概率”是义务教育阶段数学课程的重要组成部分,通过学习概率,学生可以加深对随机现象的认识,形成数据分析观念,做出合理的决策,并且提高分析问题和解决问题的能力,强化数学应用意识. 本文以2021年全国各地73份中考数学试卷为样本,对每份试卷中涉及“事件的概率”的试题进行梳理和归纳,尝试从考查内容、命题思路、复习建议三个方面进行分析,以增强对该领域内容复习教学的针对性和有效性.
一、考查内容分析
根据《义务教育数学课程标准(2011年版)》(以下简称《标准》)的要求,第三学段“事件的概率”的课程内容要求学生能通过列表、画树状图等方法列出简单随机事件所有可能的结果,以及指定事件发生的所有可能结果,了解事件的概率,同时知道通过大量的重复试验,可以用频率来估计概率. 2021年全国各地中考试题涉及“事件的概率”的试题考查比较全面,反映了《标准》的基本要求. 主要涉及以下三个部分:一是对随机现象和概率意义的认识;二是关于简单随机事件概率的计算,包括利用公式直接计算和通过列表、画树状图等方法进行计算;三是能运用概率知识解决实际问题. 既重视了对“事件的概率”的基础知识的考查,也关注了学生思维水平的发展.
从试题形式上看,关于“事件的概率”的内容,在笔者调查的73份试卷中:有17份试卷只在选择题中单独考查,其中湖北武汉卷考查了两道选择题;有20份试卷只在填空题中单独考查;有26份试卷只在解答题中单独考查;浙江湖州卷、湖北宜昌卷中选择题、填空题各考查一道题;广西玉林卷、湖北随州卷、湖南衡阳卷、湖南怀化卷、江苏扬州卷、四川广安卷中选择题、解答题各考查一道题;江苏苏州卷、四川资阳卷中填空题、解答题各考查一道题.
从试题内容上看,关于“事件的概率”的内容,在笔者调查的73份试卷中:考查随机事件的有7道题;考查用频率估计概率的约有2道题;考查简单随机事件概率计算的有54道题,其中与统计相结合的有22道题. 另外,甘肃定西卷第23题考查了用频率估计概率与列举法求概率两个知识点的结合. 可见,2021年中考“事件的概率”领域对简单随机事件概率的计算的考查依然是重点,统计与概率相结合的考查也占比很大.
从试题难度上看,关于“事件的概率”的内容,在笔者调查的73份试卷中,主要以简单题和中等难度题为主. 只有四川成都卷第25题难度较大,根源在于这道题融合了阅读理解知识点.
二、命题思路分析
1. 立足基础,考查核心概念
这类试题结合实际背景,考查“事件的概率”领域的核心概念,要求学生掌握必然事件、随机事件、不可能事件等有关概念,理解概率的意义,难度不大,通常以选择题和填空题题型出现.
例1 (广西·玉林卷)一个不透明的盒子中装有2个黑球和4个白球,这些球除颜色外其他均相同,从中任意摸出3个球,下列事件为必然事件的是( ).
(A)至少有1个白球
(B)至少有2个白球
(C)至少有1个黑球
(D)至少有2个黑球
例2 (江苏·扬州卷)下列生活中的事件,属于不可能事件的是( ).
(A)3天内将下雨
(B)打开电视,正在播新闻
(C)买一张电影票,座位号是偶数号
(D)没有水分,种子发芽
【评析】以上两道题均考查“事件的概率”的基本概念,以学生熟悉的生活场景、游戏或经验为背景,考查学生对必然事件、随机事件、不可能事件等概念的正确理解,类似的试题还有湖南怀化卷第9题、湖北武汉卷第2题、浙江湖州卷第4题等.
2. 重视方法,考查概率的计算
用列举法求概率是第三学段研究的重点模型,常以摸球、抛硬币、转圆盘、抽扑克、摸卡片、翻象棋等学生既熟悉又感兴趣的事件为载体,利用概率公式计算. 简单的情境可用枚举法、面积法等,通常在选择题或填空题中考查,稍微复杂的可通过列表或画树状图的方法列出所有机会均等的结果. 对这类题的考查不仅出现在选择题、填空题中,更多地以解答题的形式出现.
例3 (浙江·丽水卷)一个布袋里装有3个红球和5个黄球,它们除颜色外其余都相同. 从中任意摸出1个球是红球的概率是( ).
例4 (四川·泸州卷)不透明袋子中装有3个红球、5个黑球、4个白球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,则摸出红球的概率是
.
例5 (湖北·武汉卷)学校招募运动会广播员,从两名男生和两名女生共四名候选人中随机选取两人,则两人恰好是一男一女的概率是( ).
例6 (江苏·南京卷)不透明的袋子中装有2个红球、1个白球,这些球除颜色外无其他差别.
(1)从袋子中随机摸出1个球,放回并摇匀,再随机摸出1个球.求两次摸出的球都是红球的概率.
(2)从袋子中随机摸出1个球,如果是红球,不放回,再随机摸出1个球;如果是白球,放回,并摇匀,再随机摸出1个球.两次摸出的球都是白球的概率是 .
【评析】这四道题考查列举法求事件的概率,例3、例4较容易,考查学生解决一步试验的概率问题,可直接建立概率模型[P红色=红色数量总数量],可轻易计算事件的概率,类似的试题还有浙江金华卷第13题、海南卷第6题、湖南岳阳卷第11题等. 在笔者调查的73份试卷中占27道題. 例5和例6难度中等,考查用树状图或列表法解决两步试验的概率问题,关键是列举出所有等可能出现的结果数,再用概率公式计算. 两步(或以上)试验要注意“放回”与“不放回”的区别. 关于“是否放回”,例5的条件是隐性的,例6的条件是显性的. 类似的试题还有北京卷第6题、广东卷第3题、江苏无锡卷第22题等,背景以摸球游戏居多.
3. 创新背景,考查应用意识
2021年部分省、市的中考试题对“事件的概率”内容的考查越来越灵活,问题背景设计更为新颖,创新意识更强,在综合应用“事件的概率”的同时感受数学思想方法的魅力.
例7 (广西·北部湾经济区卷)如图1,小明从A入口进入博物馆参观,参观后可从B,C,D三个出口走出,他恰好从C出口走出的概率是( ).
例8 (湖南·邵阳卷)一只蚂蚁在如图2所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机选择其中一条路径,则它遇到食物的概率是 .
例9 (四川·成都卷)我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和. 如图3,ar + cq + bp是该三角形的顺序旋转和,ap + bq + cr是该三角形的逆序旋转和.已知某三角形的特征值如图4所示,若从1,2,3中任取一个数作为x,从1,2,3,4中任取一个数作为y,则对任意正整数z,此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是 .
【评析】在命制有关求简单随机事件概率的试题时,可以依据概率知识的发生、发展过程,采用文字、符号或图象等多种表征方式,并用学生以前学过的简单基本的几何或代数的知识内容为载体,从而丰富问题背景,提高试题的效度和信度,考查学生概率的模型思想与数形结合思想. 例7、例8设计巧妙,难度适中,这两个生活化的场景体现了概率最基本的知识原理和思想方法,可以激发学生的学習兴趣和解决实际问题的热情,使他们体验数学来源于生活,又服务于生活. 例9是基于阅读理解背景的通过列举法求事件的概率的一道综合题,从命题的角度来看,创新意识强,内容丰富、超越常规,考查学生的阅读理解能力、观察思考能力、分析判断能力、抽象概括能力、类比能力等,同时考查数学建模思想、数形结合思想及化归思想等.
4. 综合统计,考查随机意识
统计与概率都是研究随机现象的科学. 统计是收集、整理、分析数据,通过归纳的方法研究随机现象,而概率则是通过构建模型研究随机现象. 近年来,通过同一背景把统计和概率两种问题进行综合考查有增多的趋势.
例10 (湖南·衡阳卷)下列说法正确的是( ).
(A)为了解我国中学生课外阅读情况,应采取全面调查方式
(B)某彩票的中奖机会是1%,买100张一定会中奖
(C)从装有3个红球和4个黑球的袋子里摸出1个球是红球的概率是[34]
(D)某校有3 200名学生,为了解学生最喜欢的课外体育运动项目,随机抽取了200名学生,其中有85名学生表示最喜欢的项目是跳绳,估计该校最喜欢的课外体育运动项目为跳绳的有1 360人
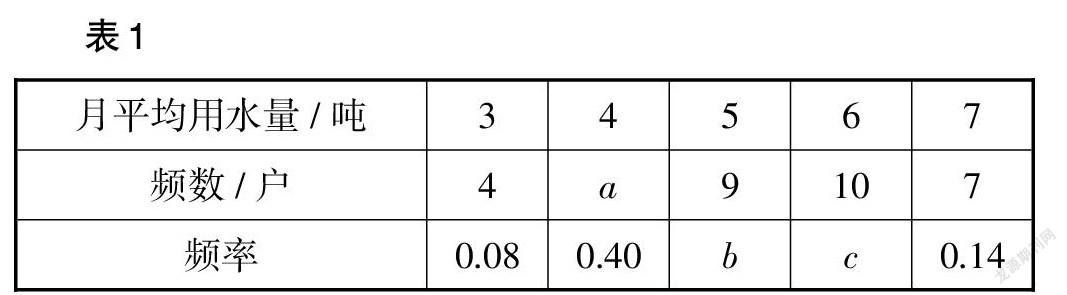
例11 (青海卷)为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如表1所示的尚不完整的统计表.
试根据统计表中提供的信息解答下列问题:
(1)填空:a的值为 ,b的值为 ,c的值为 .
(2)这些家庭中月平均用水量数据的平均数是
,众数是 ,中位数是 .
(3)根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的用户约有多少?
(4)市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中,选取两户进行“节水”经验分享. 试用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.
例12 (甘肃·定西卷)一个不透明的箱子里装有3个红色小球和若干个白色小球,每个小球除颜色外其他完全相同,每次把箱子里的小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量重复实验后,发现摸到红色小球的频率稳定于0.75左右.
(1)试估计箱子里白色小球的个数;
(2)现从该箱子里摸出1个小球,记下颜色后放回箱子里,摇匀后,再摸出1个小球,求两次摸出的小球颜色恰好不同的概率(用画树状图或列表的方法).
【评析】概率和统计的综合题有三种类型,例10属于独立型,选项之间没有关联,考查了概率的基本概念、古典概率计算公式和统计的有关知识,类似的题目只有四川广安卷第6题. 例11属于添加型,考查了平均数、众数、中位数、频数分布表,以及列表法与树状图法等知识点,前三道小题组成了一道完整的统计类解答题,为了考查“事件的概率”添加了第(4)小题,只是借用了题目背景,数据方面没有关联,这类题目的考查逐年增多,在笔者抽查的73份试卷中有22道题. 例12属于依存型,考查了统计和概率的桥梁——用频率估计概率这个知识点,只有计算出白色小球的个数后才能求事件的概率.
5. 德育渗透,考查学科素养
寓德育于各科教学内容和教学过程之中是每一位教师的职责. 作为基础学科,数学应该在德育中发挥重要作用. 在教学中应多介绍我国古代数学的研究成就,在扩大学生知识面的同时增强学生的民族自豪感,激发学生的学习动力. 同时,随着中国的快速发展,数学应用的例子在经济建设中随处可见. 因此,在教学引入中应摒弃一些过时且枯燥的例子,可以将热议时事作为素材,让学生在潜移默化中接受德育,实现德育的无痕渗透.
例13 (云南卷)为庆祝中国共产党成立100周年,某市组织该市七、八两个年级学生参加演讲比赛,演讲比赛的主题为“追忆百年历程,凝聚青春力量”. 该市一中学经过初选,在七年级选出3名同学,其中2名女生,分别记为x1,x2,1名男生,记为y1;在八年级选出3名同学,其中1名女生,记为x3,2名男生,分别记为y2,y3. 现分别从两个年级初选出的同学中,每个年级随机选出1名同学组成代表队参加比赛.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,求所有可能出现的代表队总数;
(2)求选出的代表队中的2名同学恰好是1名男生和1名女生的概率P.
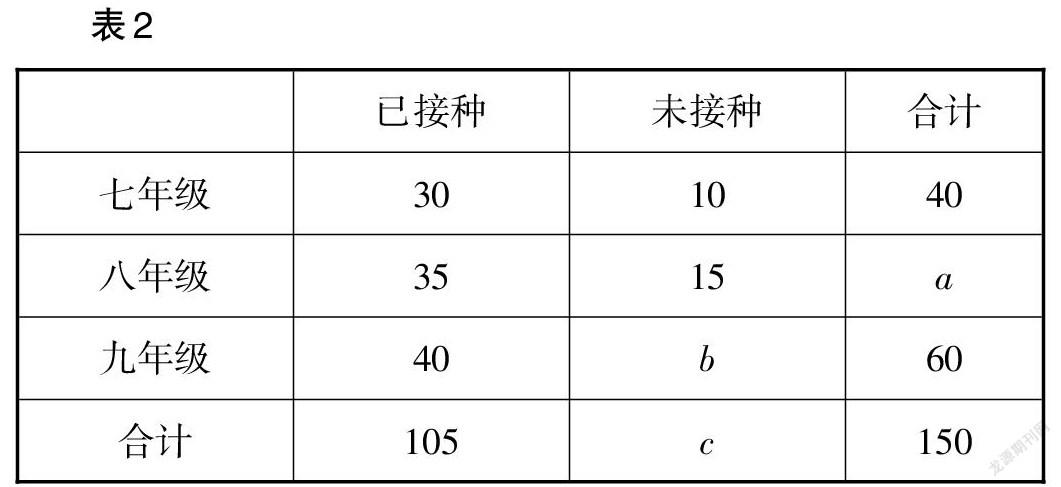
例14 (湖北·随州卷)疫苗接种初期,为更好地响应国家对符合条件的人群接种新冠疫苗的号召,某市教育部门随机抽取了該市部分七、八、九年级教师,了解教师的疫苗接种情况,得到如表2所示的统计表.
(1)表中,a的值为 ,b的值为 ,c的值为 ;
(2)由表中数据可知,统计的教师中接种率最高的是 年级教师(填“七”“八”或“九”);
(3)若该市初中七、八、九年级一共约有8 000名教师,根据抽样结果估计未接种的教师约有 ;
(4)为更好地响应号召,立德中学从最初接种的4名教师(其中七年级1名,八年级1名,九年级2名)中随机选取2名教师谈谈接种的感受,试用列表或画树状图的方法,求选中的两名教师恰好不在同一年级的概率.
【评析】例13以“庆祝中国共产党成立100周年”为情境命题,教育学生爱国爱党,立报国之志、学报国之才、践报国之行,努力学知识、学技能,从小事做起,成为对党和国家有用的人才!在笔者抽查的73份试卷中,类似的题目还有11道;例14以“接种新冠疫苗”这一热点问题开展命题,充分体现了中国特色社会主义制度的优越性,为伟大的祖国点赞!类似的题目还有3道. 另外,还有数学史、垃圾分类、禁毒宣传、节约用水等德育素材,让学生在潜移默化中接受德育教育,体现了中考的价值与魅力.
三、复习建议
回望2021年中考试题对“事件的概率”的考查,紧扣《标准》的要求,把重点放在了基本概念的理解、计算简单随机事件的概率和了解频率与概率的关系三个方面,题目背景新颖,立意不断创新,让我们深切地感受到考试评价改革带来的新气象、新景观. 针对2022年中考“事件的概率”部分的复习备考,提出如下建议.
1. 立足基础,串联知识点
回顾近几年全国各地“事件的概率”试题,从命题依据来看,以《标准》作为命题的基本依据,考查重点集中在三个方面:一是对基本概念的考查,如随机事件、概率的意义;二是通过列表、画树状图等方法列出简单随机事件所有可能的结果,以及指定事件发生的所有可能结果;三是用频率估计概率. 从试题形式和难度来看,考查单一知识点的试题较多,试题形式和难度都没有太大变化,以考查基础知识、基本技能、基本思想方法,以及分析问题和解决问题的能力为主,题目背景突出时代主题,以学生熟悉的生活场景或经验为主. 题目类型以选择题或填空题形式考查概率的基础知识,如必然事件、不可能事件、随机事件等概念和概率的意义等;以解答题形式考查用列表或画树状图求多步试验下的简单随机事件的概率. 因此,中考复习一定要立足基础,用思维导图把关于概率的知识点串联起来,如图5所示.
通过思维导图可以有效构建知识网络,厘清各知识点之间的逻辑关系,能够充分调动学生学习的积极性,推动他们主动思考,厘清思路,同时能够有效提高中考复习效率,化零为整地加深了学生对知识要点的理解与掌握.
2. 渗透思想,重视方法引路
数学思想的运用是数学学习过程的桥梁和纽带,是学生锻炼自己的综合性思维能力的最佳平台和渠道,思维的塑造和训练对于提升学生的学科素养是大有裨益的. 因此,在复习“事件的概率”内容时,应加深对题目中蕴含的模型思想、随机思想、统计思想、化归思想、数形结合思想等思想方法的理解. 值得注意的是,用列举法求概率不应在计算上做过高要求,掌握方法至关重要. 第一,学会正确使用列举法求概率. 如果试验只有一步,可直接使用枚举法;如果试验有两步,既可利用列表法,又可画树状图,列举机会均等的结果;如果试验有三步(一般不超过三步),则必须画树状图列举所有机会均等的结果. 第二,在试验过程中完成第一步之后会判断是否放回,它将直接影响机会均等的个数. 第三,理解古典概率计算公式:如果在一次试验中,有n种可能的结果,并且它们发生的可能性相同,事件A出现m种结果,那么事件A发生的概率为P(A) =[mn]. 第四,使用列表法和画树状图法需正确分析试验对象,了解试验对象是谁及它的个数. 例如,某校有A,B两个餐厅,甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐,求甲、乙、丙三名学生在同一个餐厅用餐的概率. 这是一道典型易错题,这个问题试验对象是A,B两个餐厅,所以它是三步完成的试验,每步试验的结果有两个.
3. 注重实践,提升数学活动经验
苏霍姆林斯基说过这样一句话:“当知识与积极的活动紧密联系在一起的时候,学习才能成为孩子精神生活的一部分.”概率知识来源于生活实践和生产过程中,所以在教学中可以让学生多实践,为学生提供“做数学”的机会,让他们经历“猜想—实践—分析—验证”的学习过程,亲身经历,感性认知,在实践中抽象出数学问题、构建数学模型,体会概率在决策中的作用,知道通过大量重复试验时频率可作为事件发生的概率的估计值,并获得基本的数学活动经验.
4. 传递文化,促进全面发展
义务教育阶段的数学课程,其基本出发点是促进学生全面、持续、和谐地发展,要紧扣《标准》要求,关注概率的应用性,尤其是结合生产生活实际、社会热点背景的题目,多以富有时代气息的现实问题做例子,如5G网络、抗击疫情、禁毒、垃圾分类、节约用水等,激发学生爱党、爱国的深厚情怀,引导学生修大德、明大理、立大志、行大道,努力培养担当民族复兴大任的时代新人,促使学生在推动新时代实现中华民族伟大复兴的中国梦的壮阔进程中展现青春风采.
四、模拟题欣赏
1. 下列说法正确的是( ).
(A)端午节我们有吃粽子的习俗,为了保证大家吃上放心的粽子,质监部门对市场上的粽子实行全面调查
(B)一组数据2,5,5,3,4的众数和中位数都是5
(C)某地发行一种福利彩票,中奖概率为1%,买这种彩票100张一定会中奖
(D)甲、乙两名同学各跳远10次,若他们跳远成绩的平均数相同,甲同学跳远成绩的方差为1.2,乙同学跳远成绩的方差为1.6,则甲同学发挥比乙同学稳定
答案:D.
2. 如图6,小球从[A]口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从[H]口落出的概率为( ).
答案:C.
3. 将分别标有“学”“习”“强”“国”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀. 随机摸出一球,不放回;再随机摸出一球. 两次摸出的球上的汉字可以组成“强国”的概率是 .
答案:[16].
4. 一个不透明的盒子里装有20个红、黄两种颜色的小球,这些球除颜色外其他完全相同. 每次摸球前先将盒子里的球摇匀任意摸出1个球记下颜色后再放回盒子. 通过大量重复摸球试验后发现,摸到黄球的频率稳定在0.3,那么估计盒子中红球有 .
答案:14個.
5. 小丽同学代表学校参加“我爱祖国”主题宣传教育活动,该活动分为两个阶段:第一阶段有“歌曲演唱”“书法展示”“器乐独奏”三个项目(依次用A,B,C表示),第二阶段有“故事演讲”“诗歌朗诵”两个项目(依次用D,E表示),参加人员在每个阶段各随机抽取一个项目完成.
(1)小丽同学在第一阶段抽中“器乐独奏”的概率是 ;
(2)试用画树状图或列表的方法求小丽同学恰好抽中C,D两个项目的概率.
答案:(1) [13];
(2)根据题意画如图7所示的树状图.
共有6种等可能的情况,其中小丽同学恰好抽中C,D两个项目的只有1种情况,所以小丽同学恰好抽中C,D两个项目的概率为[16].
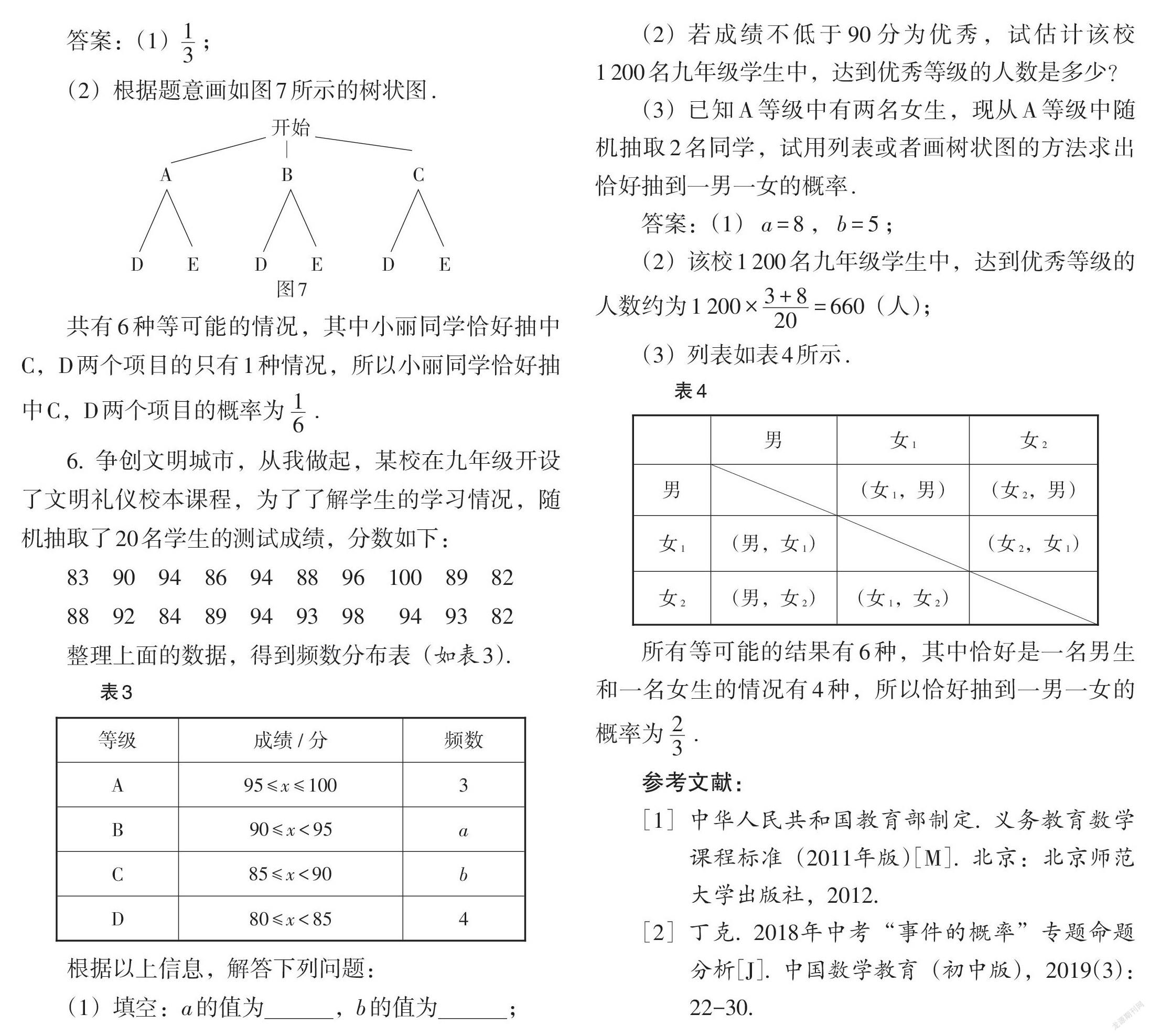
6. 争创文明城市,从我做起,某校在九年级开设了文明礼仪校本课程,为了了解学生的学习情况,随机抽取了20名学生的测试成绩,分数如下:
所有等可能的结果有6种,其中恰好是一名男生和一名女生的情况有4种,所以恰好抽到一男一女的概率为[23].
参考文献:
[1]中华人民共和国教育部制定. 义务教育数学课程标准(2011年版)[M]. 北京:北京师范大学出版社,2012.
[2]丁克. 2018年中考“事件的概率”专题命题分析[J]. 中国数学教育(初中版),2019(3):22-30.
3360501908298
