创设情境·发展思维·关注应用

2022-03-21欧光宇

中国数学教育（初中版） 2022年3期

欧光宇

摘要：“抽样与数据分析”是初中数学的主要知识之一，也是中考的重要考点之一. 文章结合2021年全国部分省、市的中考试题进行命题分析、试题解析，意在帮助读者了解全国各地中考试卷中对“抽样与数据分析”的考查内容和考试要求，供复习参考.

关键词：中考试题;统计图表;命题分析

“抽样与数据分析”是初中数学的主要知识之一，也是中考的重要考点之一. 初中生在体验数据收集、处理、分析和推断的过程中理解抽样方法，在体验用样本估计总体的过程中发展和建立数据分析观念. 2021年全国各地中考数学试卷对“抽样与数据分析”的考查遵循《义务教育数学课程标准（2011年版）》（以下简称《标准》）的要求，题型基本稳定，注重基础，考试内容主要集中在几种统计图、对基本概念的理解和应用（如抽样、平均数、众数、中位数、方差等），以及用样本估计总体，关注合情推理，着重考查样本估计总体的思想，关注样本的代表性及估计的合理性，强调统计观念.

一、考查内容分析

1. 考点及分值分析

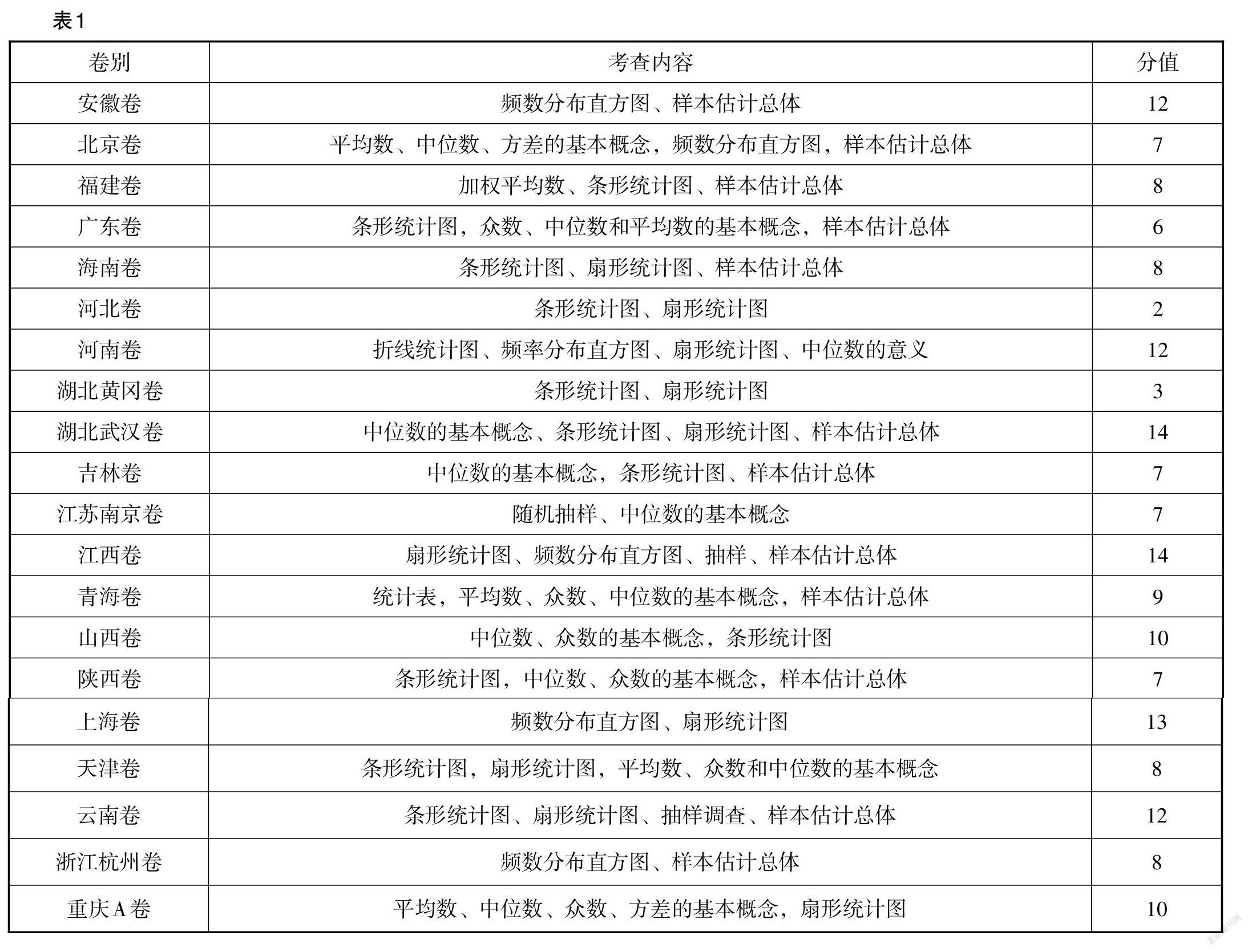
2021年中考试题，“抽样与数据分析”考查的知识点覆盖面广，部分试卷的知识点如表1所示.

2. 内容与特点分析

试题围绕着“抽样与数据分析”的基础知识和基本方法，考查学生运用“抽样与数据分析”的知识与方法分析和解决实际问题的能力，考查学生通过分析、综合建立模型并运算求解的能力，以及数据处理能力和应用意识，对能力的考查比较全面，强调综合性、应用性，并充分结合学生的实际进行考查. 以基本概念为主，着重考查样本估计总体的思想，关注样本的代表性及估计的合理性，强调统计观念.

从试题的难度上来讲，多数题目属于中、低档题，难度适中，题目的设计与学生的实际生活相联系，注重对数学思想方法、数学能力的考查，展现了数学的教育价值. 对于基本概念的考查，多数试题体现在对条形统计图、扇形统计图、折线统计图、频数分布统计表及频数分布直方图等图表的认识、含义的理解、图表的特征的考查上，对于中位数、众数、方差等概念，重视考查这些统计量的重要特征.

二、命题思路分析

2021年中考“抽样与数据分析”部分的试题，从学科的整体高度和思维能力的角度出发，将知识、能力、思想方法融为一体，全面考查了学生的数学能力和学科素养，试题关注数学的学科特点，突出了知识的基础性、综合性和应用性，以知识为主体，以教材为原型，源于教材，又高于教材，使对“抽样与数据分析”的基础知识的考查达到了必要的深度和广度，具体分析如下.

1. 考查知识全面，符合《标准》要求

考查“抽样与数据分析”的试题主要遵循《标准》的要求，考查全面，难度适中，具体考点及要求如表2所示.

（1）考查数据的收集和整理.

例1 （湖南·常德卷）舒青是一名观鸟爱好者，他想要用折线统计图来反映中华秋沙鸭每年秋季到当地避寒越冬的数量变化情况，以下是排乱的统计步骤：① 从折线统计图中分析出中华秋沙鸭每年来当地避寒越冬的变化趋势;② 从当地自然保护区管理部门收集中华秋沙鸭每年来当地避寒越冬的数量记录;③ 按統计表的数据绘制折线统计图;④ 整理中华秋沙鸭每年来当地避寒越冬的数量并制作统计表. 正确统计步骤的顺序是（）.

（A）②→③→①→④ （B）③→④→①→②

（C）①→②→④→③ （D）②→④→③→①

设计思路分析：此题以“中华秋沙鸭避寒越冬”为问题情境，完整地呈现了数据的收集、整理、描述过程，并以正确排序的问题形式呈现，这样的形式完整地考查了数据收集、整理的全过程.

（2）考查对数据的描述.

① 考查统计图的制作.

例2 （湖南·邵阳卷）某社区针对5月30日前该社区居民接种新冠疫苗的情况开展了问卷调查，共收回6 000份有效问卷.经统计，制成如表3所示的数据表格.

小杰同学选择扇形统计图分析接种不同针数的居民人数所占总人数的百分比.下面是制作扇形统计图的步骤（顺序打乱）：

① 计算各部分扇形的圆心角分别为126°，136.8°，79.2°，18°.

② 计算出接种不同针数的居民人数占总人数的百分比分别为35%，38%，22%，5%.

③ 在同一个圆中，根据所得的圆心角度数画出各个扇形，并注明各部分的名称及相应的百分比.

如图1，制作扇形统计图的步骤排序正确的是（）.

（A）②①③ （B）①③②

（B）①②③ （D）③①②

设计思路分析：此题以“社区居民接种新冠疫苗”为问题情境，从数据收集、分析到完整地制作出扇形统计图的过程，以正确排序的问题形式，考查学生制作扇形统计图的思维过程，以及准确制图的过程.

② 考查从统计图中获取信息的能力.

例3 （浙江·绍兴卷）绍兴“莲花落”，又称“莲花乐”“莲花闹”，是绍兴一带的曲艺. 为了了解学生对该曲种的熟悉程度，某校设置了：非常了解、了解、了解很少、不了解四个选项，随机抽查了部分学生进行问卷调查，要求每名学生只选其中的一项，并将抽查结果绘制成如图2、图3所示的不完整的统计图.

根据图中信息，解答下列问题：

（1）本次接受问卷调查的学生有多少人？并求图3中“了解”的扇形圆心角的度数.

（2）全校共有1 200名学生，试估计全校学生中“非常了解”“了解”“莲花落”的学生共有多少人？

设计思路分析：此题以“浙江绍兴的民间曲艺”为问题情境，题目的基本条件以“条形统计图”和“扇形统计图”展示，考查学生对统计图的理解，能从统计图中读取信息，并能解决问题. 既考查了统计图的基础知识，又考查了学生的读图能力，是一种很好的考查方式. 同时，宣传了民间艺术，传承了民族文化.

（3）考查数据分析能力.

① 考查统计量的计算.

例4 （江苏·苏州卷）为增强学生的环保意识，共建绿色文明校园，某学校组织“废纸宝宝旅行记”活动. 经统计，七年级5个班级一周回收废纸情况如表4所示.

则每个班级回收废纸的平均重量为（）.

（A）5 kg （B）4.8 kg

（C）4.6 kg （D）4.5 kg

设计思路分析：此题以“共建绿色文明校园”为问题情境，通过数据的收集、计算平均数考查学生对基本统计量的理解.

例5 （山东·聊城卷）为了保护环境，加强环保教育，某中学组织学生参加义务收集废旧电池的活动，表5是随机抽取40名学生对收集废旧电池的数量进行的统计.

试根据学生收集到的废旧电池数，判断下列说法正确的是（）.

（A）样本为40名学生

（B）众数是11节

（C）中位数是6节

（D）平均数是5.6节

设计思路分析：此题以“保护环境”为问题情境，通过收集废旧电池的活动考查学生是否能理解样本的基本含义，是否能准确回答众数和中位数，是否能计算加权平均数.

② 考查统计量的意义.

例6 （浙江·宁波卷）甲、乙、丙、丁四名射击运动员进行射击测试，每人10次射击成绩的平均数[x]（单位：环）及方差[s2]（单位：环2）如表6所示.

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（）.

（A）甲（B）乙

（C）丙（D）丁

设计思路分析：此题以“运动员参加比赛”为问题情境，通过对甲、乙、丙、丁四名射击运动员的射击成绩进行分析，选择一名成绩好且发挥稳定的运动员参加比赛，考查学生是否能准确理解平均数[x]及方差[s2]的含义.

③ 考查运算和推理能力.

例7 （福建卷）某校为推荐一项作品参加“科技创新”比赛，对甲、乙、丙、丁四项候选作品进行量化评分，具体成绩（百分制）如表7所示.

如果按照创新性占60%、实用性占40%计算总成绩，并根据总成绩择优推荐，那么应推荐的作品是（）.

（A）甲（B）乙

（C）丙（D）丁

设计思路分析：此题以“科技创新”为问题情境，通过对甲、乙、丙、丁四项作品的量化评分，考查学生对加权平均数的理解和计算. 此题还考查了学生的分析能力，以及思维过程. 甲、乙比较乙胜，丙、丁比较丙胜，乙、丙比较乙胜，所以选择选项B. 很好地考查了学生的数学思维，对不同程度的学生进行了不同的考查.

2. 素材内容丰富，联系生活实际

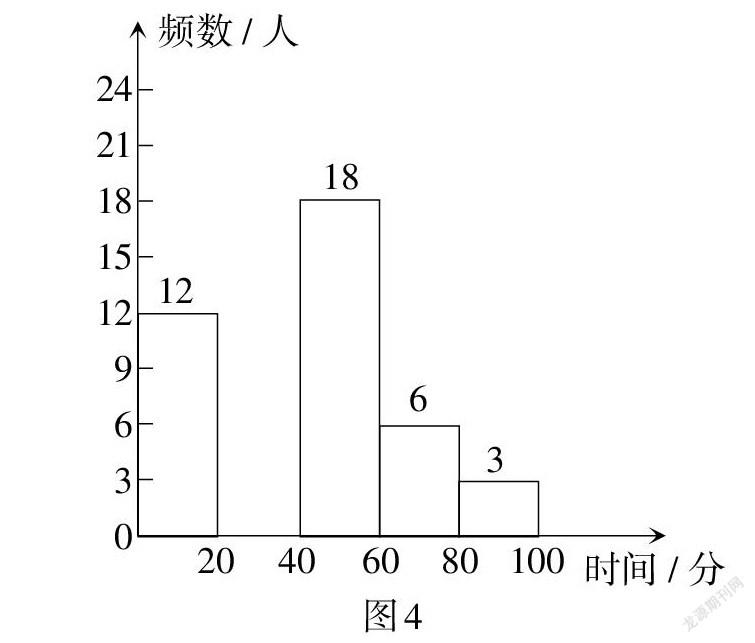
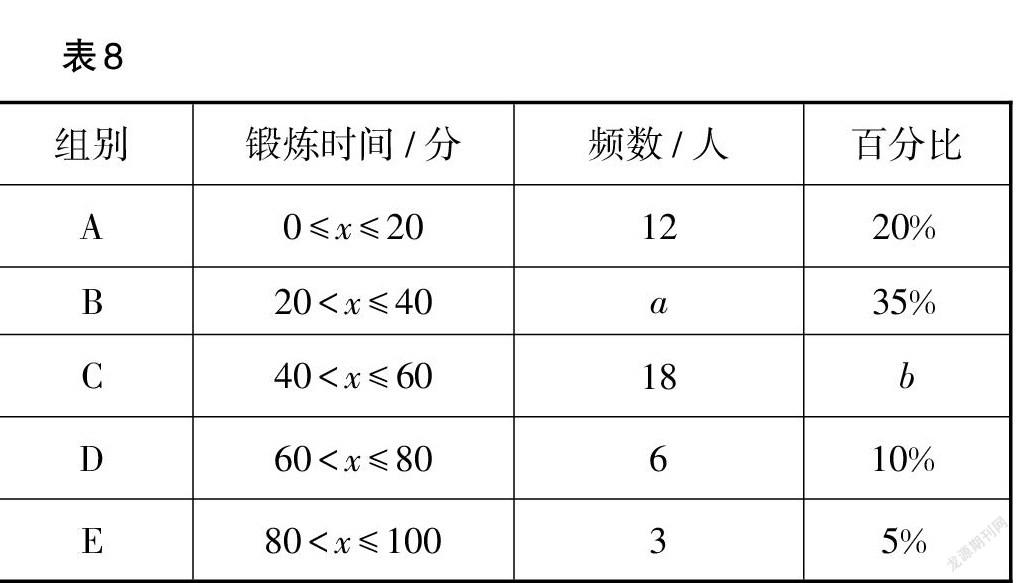
例8 （广西·贵港卷）某校为了了解本校学生每天课后进行体育锻炼的时间情况，在5月份某天随机抽取了若干名学生进行调查，调查发现学生每天课后进行体育锻炼的时间都不超过100分钟，现将调查结果绘制成两幅尚不完整的统计图表如图4、表8所示.试根据统计图表提供的信息，解答下列问题.

（1）本次调查的样本容量是 ;表中[a]的值为，[b]的值为 .

（2）将频数分布直方图补充完整.

（3）已知[E]组有2名男生和1名女生，从中随机抽取2名学生，恰好抽到1名男生和1名女生的概率是

（4）若该校学生共有2 200人，试根据以上调查结果估计：该校每天课后进行体育锻炼的时间超过60分钟的学生共有多少人？

设计思路分析：此题以学生学习生活中的体育锻炼为载体，考查样本与总体的关系，用频数分布直方图考查学生阅读统计图表的能力，考查用样本估计总体的思想，考查学生的应用能力、统计观念，并诠释了“五育并举”的教育理念.

3. 符合时代需求，突出数据处理能力

例9 （内蒙古·赤峰卷）某学校九年级有12个班，每班50名学生，为了调查该校九年级学生平均每天的睡眠时间，准备从12个班里抽取50名学生作为一个样本进行分析，并规定如下：设每名学生平均每天的睡眠时间为[t]（单位：时），将收集到的学生平均每天睡眠时间按[t≤6]，[6

（1）下列抽取方法具有代表性的是（）.

（A）随机抽取一个班的学生

（B）从12个班中，随机抽取50名学生

（C）随机抽取50名男生

（D）随机抽取50名女生

（2）由上述具有代表性的抽取方法抽取50名学生，平均每天的睡眠时间数据如表9所示.

① 这组数据的众数和中位数分别是， .

② 估计九年级学生平均每天睡眠时间[t≥8]的人数大约为多少.

（3）从样本中学生平均每天睡眠时间的[t≤6]的4名学生里，随机抽取2人，画树状图或列表，求抽得2人平均每天睡眠时间都是6小时的概率.

设计思路分析：此题以學生学习生活中的睡眠时间为载体，符合时代需求，符合教育部提出的“五项管理”的要求，突出时代性. 此题考查样本与总体的关系，以及众数、中位数和加权平均数等基本概念，考查学生阅读统计图表的能力，考查用样本估计总体的思想，考查学生的应用能力和统计观念.

4. 命题立足《标准》，原型取材教材

例10 （青海卷）为了倡导“节约用水，从我做起”，某市政府决定对该市直属机关200户家庭用水情况进行调查. 市政府调查小组随机抽查了其中部分家庭一年的月平均用水量（单位：吨），调查中发现，每户家庭月平均用水量在3～7吨范围内，并将调查结果制成了如表10所示的尚不完整的统计表.

试根据统计表中提供的信息解答下列问题：

（1）填空：[a]的值为，[b]的值为，[c]的值为 .

（2）这些家庭中月平均用水量数据的平均数是，众数是，中位數是 .

（3）根据样本数据，估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少？

（4）市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中，选取两户进行“节水”经验分享. 试用列表或画树状图的方法，求出恰好选到甲、丙两户的概率，并列出所有等可能的结果.

设计思路分析：此题倡导“节约用水，从我做起”，源于教材，又高于教材. 教材中是以一次函数模型的形式出现，此题以离散型的形式展示，给我们的思考是：初中数学要教给学生什么？怎样才能教出数学的本质，培养出数学的思维？此题考查样本与总体的关系，以及众数、中位数和加权平均数等基本概念，考查学生阅读统计图表的能力，考查用样本估计总体的思想，考查学生的应用能力和统计观念.

三、命题趋势及热点分析

“抽样与数据分析”是初中数学的重要组成部分，也是中考考查的重点内容，又是高中数学的基础. 分析2021年全国各地的中考试题，估计在一段时间内，“抽样与数据分析”都将是中考的重要考点. 解答题的难度趋于稳定，主要考查学生的数据处理能力、阅读理解能力、分析问题与解决问题的能力和应用意识.

1. 基本概念问题

对于基本概念的考查仍然是考查重点，主要考查众数、中位数、平均数、加权平均数及方差等基本概念.

2. 统计图表问题

从统计图表中读取所需的信息是学生统计知识和能力的重要体现，也是中考的热点. 解决该类问题的关键是正确理解图表中各个量的含义.

3. 取材教材问题

中考万变不离其宗，其中的“宗”指的就是教材，许多试题源于教材又高于教材.

四、中考复习建议

1. 把握《标准》，回归教材

教材中的例题、习题大多数蕴含着丰富、深刻的背景. 以教材为素材组织中考复习是提高成绩非常有效的途径. 平时学习中要用好教材，到了中考复习阶段更要以教材为主，充分发挥教材的导向作用. 这不仅能让学生跳出“题海”，又能让学生巩固基础知识，掌握数学思想方法，深化数学本质，更为重要的是能激发学生的问题意识，培养学生的综合素养，教师应在深入研究的基础上充分感悟教材的编写意图，积极开发教材的内在功能，创设问题情境. 通过改变问题的某一属性，探索问题的引申、推广、拓展，在复习阶段以教材为例、以习题为素材，深入浅出，举一反三，并进行归纳和总结.

2. 提升能力，重视应用

作为数学的精髓，数学思想方法是中考考查的重点. 数学是一门思维的学科，思维能力是数学学科能力的核心.“抽样与数据分析”为数据处理提供了工具. 另外，这部分试题以中、低档难度为主，不要练习过难习题. 以2021年考查的情况来看，试题突出考查内容的核心知识，没有偏题和怪题，侧重从数学知识、思想方法、数学能力出发，多层次、多角度、多维度地考查学生的数学素养和数学能力，在兼顾试题的基础性、综合性和应用性的同时，要重视试题的层次性，合理调控试题的难度.

五、模拟题赏析

1. 下列调查方式，你认为最合适的是（）.

（A）调查市场上某种食品的色素含量是否符合国家标准，采用抽样调查方式

（B）选出某校100米短跑最快的学生参加市运会，采用抽样调查方式

（C）检测某种品牌笔芯的使用寿命，采用全面调查方式

（D）调查央视电视剧《一诺无悔》的收视率，采用全面调查方式

答案：A.

2. 某校把学生的纸笔测试、实践能力、成长纪录三项成绩分别按50%，20%，30%的比例计入学期总评成绩，90分以上为优秀. 甲、乙、丙三人的各项成绩如表11所示（单位：分），学期总评成绩优秀的是（）.

（A）甲（B）乙、丙

（C）甲、乙（D）甲、丙

答案：C.

3. 某市为响应国家“低碳环保，绿色出行”的号召，投放“共享单车”供市民出行时租用. 寒假期间，七年级数学兴趣小组对某投放点的租车情况进行一周的调查，并把收集的数据绘制成如图5、图6所示的频数分布直方图和扇形统计图.