论“数学化、本土化”的深度学习

2022-03-21段海军马旭

数学教学通讯·高中版 2022年1期

段海军　马旭

[摘要] 对于深度学习理念在我国的发展现状，提出要对其进行“数学化”和“本土化”改造.由此，文章研究了融入我国数学教育界关于高效数学学习代表性观点的深度学习理念，并定义了“数学深度学习”，进而阐述了导向数学深度学习的教学建议.

[关键词] 数学教学;深度学习;数学深度学习

问题提出

教育领域中的深度学习1976年就被提出，长期在我国乏人问津，却在近几年乘着人工智能的浪潮变成“时髦名词”. 讨论得越热烈就越要对其进行冷思考！一个关键的问题在于深度学习被提出至今，其因宽泛的内涵而多在教育理论层面被讨论而未被有效实践化，所以对其必须进行两项改造：其一，深度学习理念需要“数学化”. 张奠宙指出：“数学教育不能离开一般教育规律的指导，但是数学教育必须研究自己的特殊规律. ‘去数学化’倾向会危及数学教育的生命.”[1]正如各学科核心素养定义的不同，每个学科“深在哪儿”也是不同的，所以深度学习必须要具体科目具体分析，即深度学习必须学科化.其二，深度学习理念需要“本土化”. 作为“舶来品”的深度学习以西方国家的经验为原型，这些经验无法直接毫无保留地用于我国. “入乡必须随俗”，否则必定“水土不服”，无法有效地指导教学甚至引起教师理念上的混乱. 那么如何实现“两化”呢？可以采取这样的思路，给深度学习理念融入我国数学教育界关于高效数学学习的代表性观点，并定义它，进而再进行其他方面的探讨.

深度学习定义的概述

“深度学习”（Deep Learning）这个概念最早是由在瑞典哥德堡大学工作的两位教育心理学家Ference Marton和Roger Saljo于1976年联名发表的《On qualitative differences in learning： I-Outcome and process》一文中提出来的.此后45年来，众多国内学者对其进行了研究.对国内学者关于深度学习定义的研究进行梳理分析，将其分为三个时期.

第一个时期是引进翻译期. 这个时期的代表学者是黎加厚（引进深度学习且是我国最早对深度学习进行概念界定的研究者），他在与何玲合作发表的论文中提出：“深度学习是指在理解学习的基础上，学习者能够批判性地学习新的思想和事实，并将它们融入原有的认知结构中，能够在众多思想间进行联系，并能够将已有的知识迁移到新的情境中，作出决策和解决问题的学习.”[2]深度学习引自国外，所以这个时期的研究者大多通过翻译国外文献进行研究，所以这个时期的研究成果显得模仿意味浓厚，并且不可避免地产生了纰漏，见微知著，一些研究者把Ference Marton和Roger Saljo的国籍写错为美国.第二个时期是研究深入期. 这个时期的代表学者是张浩、安富海和郭华. 张浩强调深度学习的理解和认识可从学习科学和心理学中寻找到丰富的理论源泉，并主要分析了建构主义、情境认知理论对深度学习的解释和影响，以及分布式认知理论和元认知理论对深度学习引导与调节的理论意义. 他认为深度学习是一种主动的、批判性的学习方式，也是实现有意义学习的有效方式[3]. 安富海研究了促进深度学习的课堂教学策略，并提出：“深度学习是一种基于理解的学习，是指学习者以高阶思维的发展和实际问题的解决为目标，以整合的知识为内容，积极主动地、批判性地学习新的知識和思想，并将它们融入原有的认知结构中，且能将已有的知识迁移到新的情境中的一种学习.”[4]郭华系统全面地论述了深度学习的内涵和意义，他认为深度学习，就是指在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程[5].第三个时期是反思总结期. 这个时期的代表学者是李松林和吴永军. 李松林认为深度学习是借助具有整合作用的实际问题激活深层动机，展开切身体验和高阶思维，促进深度理解和实践创新，进而对学习者产生深远影响的学习样态[6]. 吴永军认为先前学术界关于“深度学习”的研究以及实践成果有一种“单向度取向”——过于关注学生大脑内部“信息加工”过程，忽视了社会文化、情感、精神以及价值过程.他呼吁超越认知心理学的局限，建构一种全域或全视角的深度学习观. 他认为深度学习是指特定的社会文化情境中，学习者在与他人互动以及环境互动中，关注知识之间的有机联系，最终能够迁移并解决实际生活问题的意义生成的过程[7].

上述给出了6种深度学习的定义，提取其中的关键词（例如，在黎加厚对深度学习的定义中选取5个关键词：理解，批判，融入，整合，迁移;含义相近的关键词进行了统一），总计25个.统计频数大于等于2的关键词，图示如下：

据图1可知，深度学习理念经过45年、三个时期的发展后，学者们对其的定义达成了一定的共识，深度学习理念足以在我国进入第四个发展时期——“学科应用期”.为促使深度学习理念更加明确地指导数学教学，必须给数学学科的深度学习进行概念界定，即定义“数学深度学习”.

给“数学深度学习”下定义

1. 如何定义

要基于深度学习理念的内核. 通过对上图的分析，深度学习理念的核心就是“个体学习活动的解放”. 在学习方式上体现为“沉浸式学习”，即学习者全身心地投入学习中，学习者在学习中达到一种“无我”状态. 正如“无我之境，以物观物，故不知何者为我，何者为物”;在知识理解上体现为主体和客体的绝对匹配，深度学习者追求把作为客体的学习对象和作为主体的自己进行对接、调试最后到达完美的匹配状态;在持续时间上体现为一体式的学习，深度学习贯穿学习过程的始终，贯穿学习活动的方方面面.

要融入我国数学教育界关于高效数学学习的代表性观点. 深度学习当然主要体现为高效数学学习，但通过知网查阅发现，我国数学教育界关于高效数学学习研究的主要代表学者是王光明、史可富、涂荣豹. 从他们的研究成果中提炼了以下定义“数学深度学习”的要点：（1）把思维品质作为定义的核心. “数学是思维的体操”，这是一句耳熟能详的名言. 史可富认为数学是关于思维的科学，学生在数学学习过程中，数学思维的形成、发展是判断数学学习“含金量”的重要指标. 数学思维的训练，是数学教育的本原目标，数学思维能力是高效数学学习的根本特征[8]. 所以数学深度学习的定义较之一般深度学习应该着重突出思维品质的重要性. （2）体现高效数学学习的心理特征和学习者在知识建构上的反思性.王光明的研究结论表明：“心理机制、元认知、学习策略、非智力因素和数学学习素养是高效数学学习心理特征的五个结构要素. 一位数学学习效率高的学生应当以非智力因素为学习的动力源泉，以较为完善的心理机制作为前提，以高水平的元认知作为监控系统，以有效的学习策略作为学习保障，以较高的数学学习素养作为学习过程中的思维品质的体现.”[9]涂荣豹认为反思性数学学习的优势是可以帮助学生从例行公事的行为中解放出来，帮助他们学会数学学习，可以使学生的数学学习活动成为有目标、有策略的主动行为，可以使学习成为探究性、研究性的活动[10].

2. 数学深度学习的定义

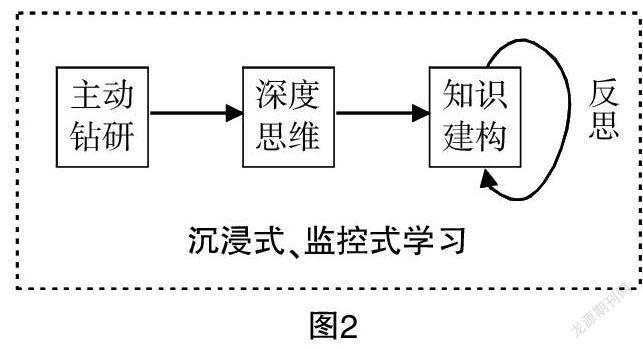
基于上述定义思路，“数学深度学习”是指学习者在学习方式上具有主动性、钻研性，思维品质上具有深刻性、宽阔性、延续性，知识建构上具有反思性、批判性并且学习全程体现沉浸性和监控性的数学学习方式.数学深度学习的结构大致图示如下：

“深在起点”——学习方式具有主动性、钻研性的数学学习. 数学深度学习的学习者真正发自内心想弄清楚数学中的定义、概念、公理、定理、公式，而并非只是死记硬背.例如同样学习诱导公式，有学生仅仅只想记住“奇变偶不变，符号看象限”这个口诀，而并不在乎它的原理是什么. 进行数学深度学习的学生则不然，他们迫切地想搞明白知识的来龙去脉.

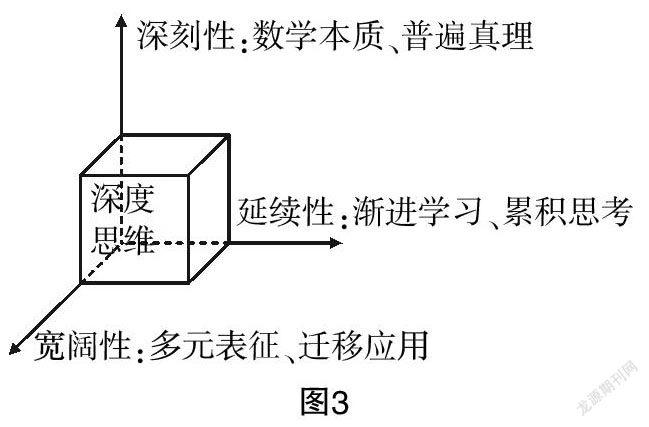
“深在过程”——思维品质上具有深刻性、宽阔性、延续性的数学学习. 何为深刻性？第一，数学深度学习是朝向数学本质的学习. 远非只是关注知识，数学深度学习者一直瞄准知识背后的数学思想方法. 例如对于诱导公式，为什么要把k+α，k∈Z中的α看做锐角？数学深度学习者可以理解把α看做锐角只是在所有情况中选取了一个特殊情况，只不过此时的k+α的具体符号反映了符号的变化，本质就是一个特殊情况可以反映一般情况而已，那么就用这个特殊情况. 所以徐利治提出数学学习的“懂”分为浅懂和真懂，所谓的浅懂就是表面的懂，没有弄明白数学概念的形成过程，没有弄明白解决问题的来龙去脉，是“见树木不见森林”;真懂或彻悟是对数学的理论、方法或定理能洞察其直观背景，并且看清楚它是如何从具体特例过渡到一般（抽象）形式的. 能用自己的语言随时把它复述出来，数学的理论、方法或定理就好像是自己发现的一样[11]. 第二，数学深度学习是朝向普遍真理的学习. 在抽象的意义下，一切科学都是数学. 深度学习者的思维超出数学学科，寻求将数学真理推广到一般事物. 何为宽阔性？第一，数学深度学习者具有以符号语言为中心的数学多元表征的能力. 数学多元表征是指同一个数学学习对象用叙述性（语言）和描绘性（视觉化表征）两类本质不同的表征的多种形式所表征[12].比如对于“函数的单调性”，大部分学生都具有两种表征，第一种是图像的上升和下降，另一种就是文字化的定义. 但浅层学习的学生无法将单调区间上任取两数和图像上任取两点对应理解，而深度学习者则可以明确. 第二，数学深度学习者注重数学的迁移应用. 深度学习强调信息整合，这种整合首先是多学科知识和多渠道信息的整合[3]. 数学是一切科学的基础，数学能力常常是求解学科交叉问题的核心. 例如用向量的加法法则求解物理中的动态平衡问题，用概率公式求解生物中的遗传问题，用方程法求解化学中的反应方程式配平问题. 何为延续性？数学深度学习者的思维过程是渐进学习和累积思考的结合体.数学深度学习者对一个知识模块的深入理解不是一蹴而就的，而是需要一段甚至特别漫长的时间去消化. 他们并不在乎短期的成绩，而瞄准当前心中的疑惑，所以可能因此会消耗大量的时间，通俗来说，就是常常“钻牛角尖”，但是对于他们来说，这个时间的占用是必要的. 为直观起见，把数学深度学习的思维结构用图示展现，并称其为“深度思维立方体”：

“深在结果”——知识建构上具有反思性、批判性的數学学习. 建构反思是指学习者在知识整合的基础上通过新、旧经验的双向相互作用实现知识的同化和顺应，调整原有认知结构，并对建构产生的结果进行审视、分析、调整的过程[4]. 反思的过程就是学生知识结构螺旋化上升的过程，从而循序渐进地接近知识的数学本质.

导向数学深度学习的教学建议

1. 坚持“四基”教育

张奠宙指出：“中国数学教育成功的关键在于‘四基’”[13]，“四基”是中国特色数学教育体系的核心理念. “四基”数学教学绝非忽视学生的发展，恰恰相反，打好基础的目的就是为了获得更切实、更有效率的全面发展，是要在良好的数学基础上谋求学生的数学发展[14]. 而学生实现数学深度学习的前提是其基本功足够扎实，所以一定要坚持“四基”教育，切不可“喜新厌旧”，否则就会丢失原有的优势.

2. 传授与数学学习相关的心理学知识

“大脑不是一个要被填满的容器，而是一个需被点燃的火把”，但学校教学中存在太多“着急”传授知识而无视学生心理发展的情况. 教育心理学界普遍认为，元认知在整个智力活动中处于支配地位，对整个活动起控制调节作用.数学教育界持相同观点，认为数学元认知在数学认知过程中具有重要作用[15]. 但是很多学生根本没有“元认知”这样的概念，特别当学生处于深度学习状态时，其认知负荷特别大. 所以了解一些与数学学习相关的心理学知识有利于学生对自己的数学学习进行监控、评价、调整，使其懂得“我应该怎么样才能更好地学数学”. 因此本研究认为传授数学学习相关的心理学知识（特别是关于数学学习心理的相关成果）可以引发学生数学深度学习，并且该策略具有很强的可行性，从事数学基础教育的大部分教师都是师范出身，学习过一定的心理学知识.基于此，编制了如下表格（表1）.

3. 定期组织绘制思维导图

思维导图是反映事物联系的良好工具. 思维导图是用图表来组织和阐述表达知识和思维过程的工具[16]，能直观、形象、有效地呈现知识间的关联、体现学生的思维过程，它具有两大特性：可视化和聚散性. 可视化特性将学生内隐式的知识建构呈现出来，有助于学生对自己认知结构的审视和反思，而聚散性特性使得知识框架兼具发散和收敛作用[17]，既有利于培养学生思维品质的高度，又有利于培养学生思维品质的宽度. 张奠宙指出：“数学知识之间存在着紧密联系，特别是数学知识之间的逻辑关系，但更深层次的知识联系，是数学内涵上的发展与联结”[18]. 所以绘制思维导图应该以“数学本质”为主线.

4. 强调数学的跨学科应用

数学深度学习着意迁移运用. 所以建议教师在讲解完数学题目后，呈现对应的数学思想方法在其他理科中的应用. 这样的设计原因有二：首先当前国际教育发展大趋势——STEAM教育强调知识跨界、场景多元. STEAM教育是一种基于科学（Science）、技术（Technology）、工程（Engineering）、艺术（Art）、数学（Mathematics）的跨学科教育，它倡导教学要超越学科教学的概念，注重知识与现实世界的联系;要交叉融合各个学科，使其相互支撑，相互补充，在学科间的相互碰撞中培养学生各方面技能和认知. 其次我国近几年高考题也开始出现学科交叉融合的题目，例如2019新课标二卷理科数学的第四题考查物理和数学的融合，2020年新课标三卷理科数学的第四题考查生物和数学的融合.

数学的跨学科应用要成为学生深度学习的途径. 跨学科应用主要在培养学生的迁移运用能力，但是数学的跨学科应用通常被简单化为“数学是其他科目的工具”，其应该成为学生深度学习的有效途径，这种迁移训练可以丰富学生对数学知识的表征.

反思

自近代以来，每当国外特别是西方的教育理论传入我国，往往被奉为圭臬.辛亥革命后我们学赫尔巴特的“旧三中心”，五四运动后学杜威的“新三中心”，新中国成立后学凯洛夫，21世纪初，经济合作与发展组织（OECD）率先提出了“核心素养”结构模型，我国又掀起来“核心素养”热潮并持续到今天. 有些确实是取其精华，但是有些没有去其糟粕，撰写文章时大肆追捧国外一些光怪陆离没有实践效果的概念和理论是一种“内伤”. 批判吸收是我们对于一切学问借鉴与学习的准则，所以以后对任何自国外引进的教育理论，都要对其进行“本土化”改造后，方能为我所用.

参考文献：

[1] 张奠宙，赵小平. 当心“去数学化”[J]. 数学教学，2005（06）：50.

[2] 何玲，黎加厚. 促进学生深度學习[J]. 现代教学，2005（05）：29-30.

[3] 张浩，吴秀娟. 深度学习的内涵及认知理论基础探析[J]. 中国电化教育，2012（10）：7-11+21.

[4] 安富海. 促进深度学习的课堂教学策略研究[J]. 课程·教材·教法，2014，34（11）：57-62.

[5] 郭华. 深度学习及其意义[J]. 课程·教材·教法，2016，36（11）：25-32.

[6] 李松林，贺慧，张燕. 深度学习究竟是什么样的学习[J]. 教育科学研究，2018（10）：54-58.

[7] 吴永军. 关于深度学习的再认识[J].课程·教材·教法，2019，39（02）：51-58+36.

[8] 史可富，孙志慧，李冬胜. 高效数学学习的学生心理特征模型[J]. 数学教育学报，2006（04）：79-82.

[9] 王光明，佘文娟，宋金锦. 基于NVivo10质性分析的高效数学学习心理结构模型[J]. 心理与行为研究，2014，12（01）：74-79.

[10] 涂荣豹. 试论反思性数学学习[J]. 数学教育学报，2000（04）：17-21.

[11] 沈威. 徐利治数学教育思想研究[J]. 数学教育学报，2019，28（01）：74-78.