核心素养视域下的高中教材习题比较研究
2022-03-21黄玉鲜周莹陈基河
黄玉鲜 周莹 陈基河



[摘 要] 基于数学核心素养评价框架,对人教新版、人教A版、人教B版和北师大版四个版本数学教材的“概率与统计”习题进行比较分析,研究表明:从数学核心素养类型上看,就总体而言,四大素养在四版本教材习题均有体现,且数据分析素养的习题占比最高,就四大素养在不同版本教材习题中的分布情况而言,各版本教材同中存异;从数学核心素养水平上看,就总体而言,四版本教材的知识创新水平习题占比较低,就各大素养的不同素养水平在各版本教材习题中的分布情况而言,各版本教材异中存同.
[关键词] 数学核心素养;教材比较;概率与统计;习题
引言
数学核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度、价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的[1]. 教材是体现课程标准的理念、目标和内容, 直接指导课程实施的潜在实施课程[2],而习题作为数学教材的重要组成部分,是发展学生数学核心素养的重要平台[1]. 通过查阅文献发现,目前,数学核心素养的研究大多集中在理论研究、考试研究以及培养研究等方面,而基于核心素养视域下的教材习题研究很少.基于以上背景,本文着手对比分析高中不同版本教材“概率与统计”习题在数学核心素养上的体现,以期为教师的教学和教材的编写提供一定的参考建议.
研究设计
(一)研究对象
本研究以2007年教育部审定的人民教育出版社A版数学必修3、B版数学必修3、2014年教育部审定的北京师范大学出版社数学必修3、2019年教育部审定的人民教育出版社数学必修第二册(以下分别简称“人教A版”“人教B版”“北师大版”“人教新版”)这四个版本教材中“概率与统计”部分的习题为研究对象.
(二)数学核心素养评价框架的确定
新课标给出了数学核心素养的三个水平划分标准,但喻平教授[3]指出新课标给出的数学核心素养水平划分标准对日常的学习评价没有直接的指导意义,故喻平教授在分析已有成熟的理论基础上,提出数学核心素养的水平划分标准,将数学核心素养划分为“知识理解”“知识迁移”“知识创新”三个水平.
本研究根据喻平提出的数学核心素养水平划分标准及新课标中对本研究涉及的四大数学核心素养的概念界定(因必修课程“概率与统计”内容不重点培养数学抽象、直观想象两个素养,故将这两个素养除去[1]),创建以下数学核心素养评价框架(见表1).
(三)习题的素养类型及素养水平的确定
新课标指出必修课程“概率与统计”内容重点培养数据分析、数学建模、逻辑推理、数学运算这四个素养[1],故本研究假设教材中的每道“概率与统计”习题最少体现一种数学核心素养.依据上述的数学核心素养评价框架,对四个版本教材中“概率与统计”习题的数学素养类型和数学素养水平进行编码,以下列教材习题的编码为例,详细说明编码原则.
北师大版示例:小军、小燕和小明是同班同学,假设他们三人早上到校先后的可能性是相同的.
(1)事件“小燕比小明先到校”的概率是多少?
(2)事件“小燕比小明先到校,小明又比小军先到校”的概率是多少?
分析:此题记为一题,解决此题需要学生在新的情境中,运用古典概型解决问题,此外还需要进行基本的运算,故此题体现了数据分析、数学建模、数学运算三个核心素養,其中数据分析和数学建模两个素养属于知识迁移水平,数学运算属于知识理解水平.
(四)数据的统计方法和结果
首先,统计各版教材“概率与统计”习题中体现某个素养类型的习题数量,并将其除以对应版本教材的“概率与统计”习题总数,得到相应版本考查某一素养类型所占的习题数量比重.接着,统计每个版本教材在各个素养上达到不同素养水平的习题数,并计算其在对应版本习题总数中所占的百分比.最后,依据此数据统计方法,得到如表2、表3所示的结果.
研究结果与分析
(一)习题在素养类型上的分布
为了直观地比较分析四个版本教材习题在素养类型上的数量百分比,基于表2绘得图1.
1. 四大素养在四版本教材习题中的总体分布情况
由图1可知,四版本教材“概率与统计”习题在数据分析素养的习题占比最高,四版本教材在该素养类型的习题占比均达到90%以上;在数学运算和逻辑推理两个素养类型的习题数量百分比次之;在数学建模素养类型的习题占比较低.由此可见,四大素养在四版本教材习题均有体现,且数据分析素养的习题占比最高.
2. 四大素养在不同版本教材习题中的分布情况
由图1可知,在数据分析素养和数学运算素养上,四版本教材的习题占比相差较小;在数学建模素养和逻辑推理两个素养上,四版本教材相差较大,其中在数学建模素养上,北师大版的习题占比最高,人教A版的习题占比次之,人教新版和人教B版的习题占比较低;在逻辑推理素养上,北师大版的习题占比最高,人教新版和人教A版的习题占比次之,人教B版的习题占比较低.
由此可见,四版本教材习题均突出数据分析和数学运算两个素养,而在数学建模素养和逻辑推理两个素养上,四版本教材相差较大,相对其他版本,北师大版习题更强调数学建模和逻辑推理两个素养.
(二)习题在素养水平上的分布
1. 素养水平在四版本教材习题中的总体分布情况
由表3可知,总体上,四版本教材习题的数学核心素养达到知识理解水平和知识迁移水平的习题占比较高,达到知识创新水平的习题占比较低.
2. 各大素养的不同素养水平在各版本教材习题中的分布情况
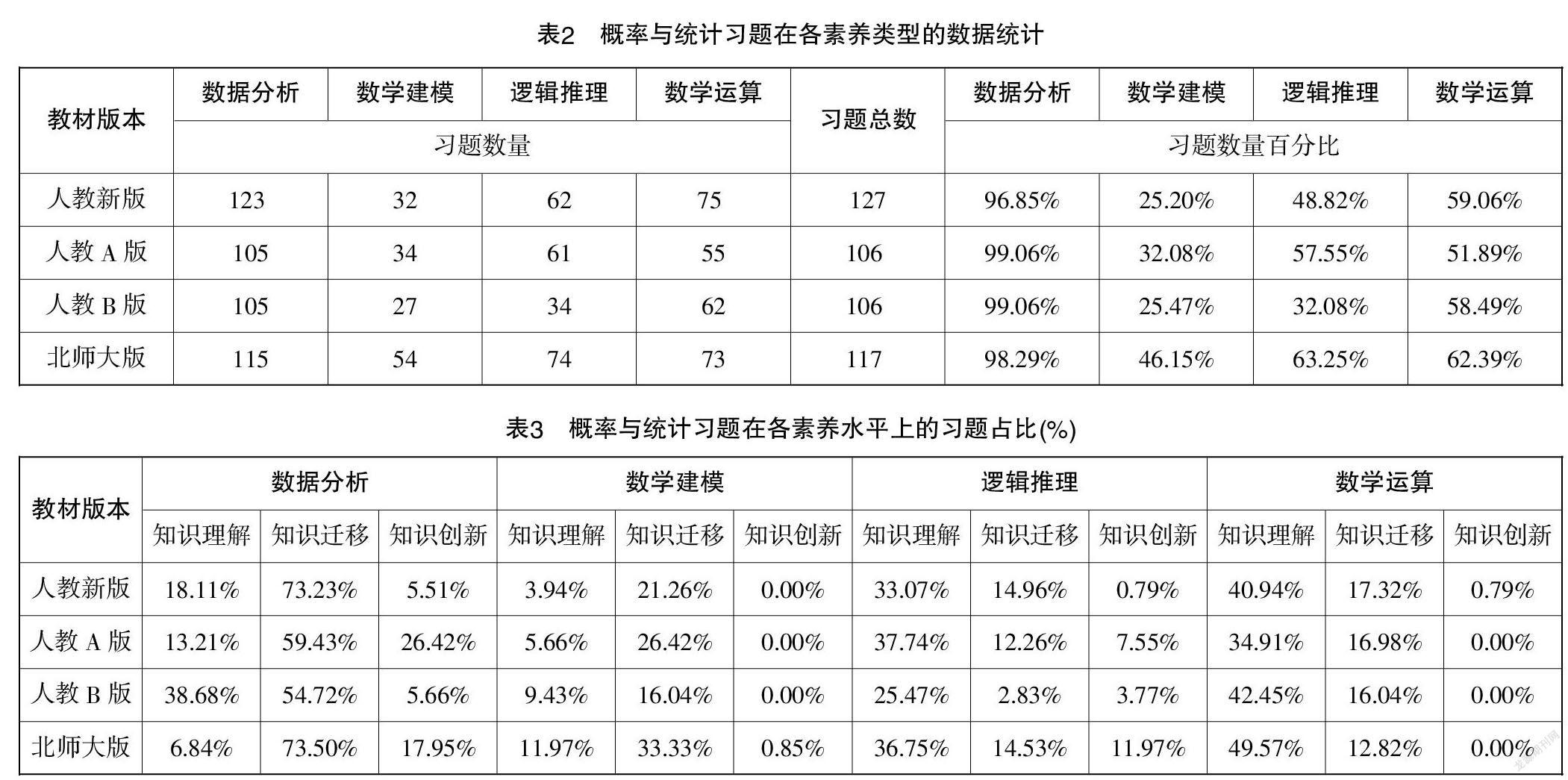
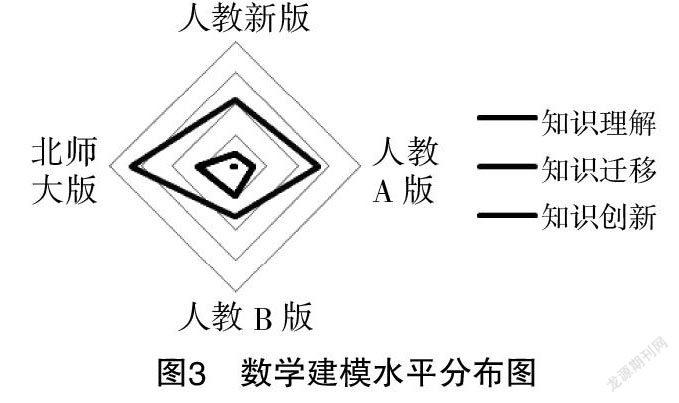
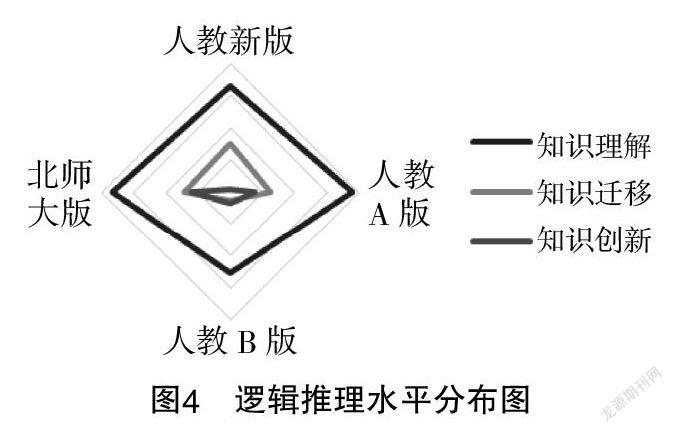
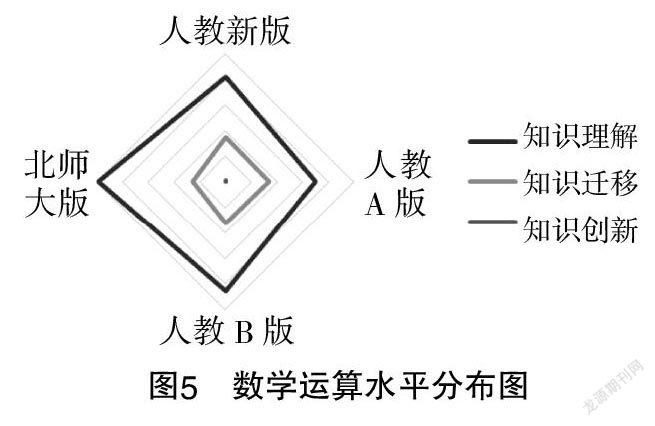
基于表3绘制了各素养水平的雷达图(见图2至图5),进一步探讨各版本教材习题在各个素养上达到不同素养水平的情况.
就数据分析素养而言,由表3和图2可知,在知识理解水平上,人教B版的习题占比最高,人教新版和人教A版的习题占比次之,北师大版的习题占比最低;在知识迁移水平上,人教新版和北师大版的习题占比较高,人教A版和人教B版的习题占比较低;在知识创新水平上,人教A版和北师大版的习题占较高,人教新版和人教B版的习题占比较低.
由此可知,在数据分析素养方面,相对其他版本教材,人教B版更强调知识理解水平,人教新版和北师大版更强调知识迁移水平,人教A版和北师大版更强调知识创新水平.
就数学建模素养而言,由表3和图3可知,在知识理解层面上,北师大版和人教B版的习题占比较高,人教新版和人教A版的习题占比较低;在知识迁移水平层面上,北师大版的习题占比较高,人教新版和人教A版的习题占比次之,人教B版的习题占比较低;在知识创新层面上,四版本教材的习题占比均较低,且四个版本教材中仅有北师大版的习题占比不为零.
由此可知,在数学建模素养方面,四版本教材均没有突出知识创新水平,且相对于其他版本教材习题,北师大版和人教B版的习题更强调知识理解水平,北师大版更强调知识迁移水平.
就逻辑推理素养而言,由表3和图4可知,在知识理解水平和知识迁移水平上,人教新版、人教A版、北师大版的习题占比相差不大,人教B版与其他三个版本教材习题占比相差较大,且占比最低;在知识创新水平上,人教A版和北师大版的习题占比较高,人教新版和人教B版的习题占比较低.
由此可知,在逻辑推理素养方面,相对于人教B版,其他三个版本的习题更加突出知识理解和知识迁移两个水平,相对于人教新版和人教B版,人教A版和北师大版习题更突出知识创新水平.
就数学运算素养而言,由表3和图5可知,在知识理解、知识迁移和知识创新三个水平上,四版本教材习题占比相差不大,其中在知识创新水平上,四版本教材的习题占比均较低,且仅有人教新版的习题占比不为零.
研究结论与思考
(一)研究结论
从数学核心素养类型上看,就总体而言,四大素养在四版本教材习题均有体现,且相对其他三个素养,数据分析素养的习题占比最高;就四大素养在不同版本教材习题中的分布情况而言,各版本教材同中存异,即四版本教材习题均突出数据分析和数学运算两个素养,而在数学建模和逻辑推理两个素养上,四版本教材相差较大,相对于其他版本,北师大版习题更强调数学建模和逻辑推理两个素养.
从数学核心素养水平上看,就总体而言,四版本教材的知识创新水平习题占比较低;就各大素养的不同素養水平在各版本教材习题中的分布情况而言,各版本教材异中存同,如在数学建模素养方面,四版本教材均没有突出知识创新水平,且相对于其他版本教材习题,北师大版和人教B版的习题更强调知识理解水平,北师大版更强调知识迁移水平.
(二)研究思考
1. 教师补充习题时,应关注开放题和考查数学建模素养的习题
开放性习题有利于学生数据分析观念的培养,增强其运用统计分析解决问题的能力﹐并加深学生对统计思想的理解[4]. 然而研究发现,四版本教材习题在素养水平中,创新水平的习题占比较低,也意味着教材中开放性习题的占比较低,这启示教师在学生完成数学教材习题的基础上,适当补充适合学生发展的开放性的习题,如增设利用概率与统计知识判断生活中相关事件的好坏程度的开放性习题,这有助于培养学生的不确定性统计思维.
数学建模素养是概率与统计内容重点培养的素养类型之一[5],而在概率统计中应用数学建模思想有利于提高学生运用数学知识解决实际问题的能力,帮助学生更好地理解和掌握所学的知识[6]. 但通过研究发现,四版本教材习题考查数学建模的习题占比相对较低,这也启示教师在学生完成数学教材习题的基础上,增设考查概率与统计知识的数学建模习题,如在几何概型内容中可以增设类似“会面问题”的生活实例,给予学生运用数学模型解决生活中实际问题的机会,调动学生学习的积极性,培养学生的关键能力.
2. 教师应充分利用不同版本教材习题的优势,注重因材施教
就数学素养类型和数学素养水平而言,不同版本教材习题各具特色,如在素养类型上,相对其他版本,北师大版习题更强调数学建模和逻辑推理两个素养,在素养水平上,就数据分析素养而言,相对其他版本教材,人教B版更强调知识理解水平,人教新版和北师大版更强调知识迁移水平,北师大版和人教A版更强调知识创新水平. 教师进行教学时,可以充分利用各个版本教材习题的优势,合理配置习题,进而更全面地培养学生的数学核心素养[7],同时依据学情,重新配置三个素养水平的习题的比例,对于基础薄弱的学生,可以适当增加知识理解水平习题的比例以促进学生对知识的理解;对于学有余力的学生,可以适当增加知识创新水平习题的比例以满足学生自主探索的欲望,拓宽学生的数学视野.
参考文献:
[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M]. 北京:人民教育出版社,2018.
[2]周莹,廖丽红,梁鑫,黄怀芳. 初中数学教材与课程标准的一致性研究——以“人教版”和“湘教版”中的函数习题为例[J].数学通报,2017,56(05):6-9+14.
[3] 喻平. 数学核心素养评价的一个框架[J]. 数学教育学报,2017,26(02):19-23+59.
[4]王建波. 三个版本初中数学教材统计习题比较研究[J]. 数学通报,2014,53(04):14-18+23.
[5]李华,胡典顺. 基于数学核心素养评价框架的试卷测评研究——以2019年高考全国卷为例[J]. 数学教育学报,2020,29(02):18-23.
[6]郑铭海. 数学建模思想在概率统计教学中的应用[J]. 中国高新区,2018(03):78.
[7]刘存华,王亚婷,周莹. 数学核心素养视域下的高中教材习题比较研究——以“三角函数”为例[J]. 数学教学研究,2019,38(05):50-53.
3808501908250
