融入数学文化 考查核心素养

覃淋　喻晓婷　张静

[摘  要] 对2018—2020年高考数学全国卷中的数学文化试题进行统计分析，研究后发现：高考数学全国卷一直在积极探索如何将数学文化与高考数学试题相结合，将数学文化融入数学试题，考查数学学科核心素养. 高考数学全国卷将数学文化、数学试题与数学学科核心素养三者有机融合后进行考查，引导学生“会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界”.

[关键词] 高考;全国卷;弘扬;数学文化;探索

引 言

“数学文化”一词，是美国数学家怀尔德（R. L. Wilder）于1981年在《作为一种文化体系的数学》（Mathematics as a Culture System）中提出的，他从数学人类学的角度提出了“数学作为一种文化体系”的观点. 这一观点为研究数学的发展展现了一个新的视角，也为数学教育研究注入了新鲜的血液. 数学文化是提升学生数学核心素养的重要手段，具有非常重要的教育价值与文化价值. 从数学文化的角度来研究高考试题，是改进高中数学命题与教学改革的一个重要突破口.

《普通高中数学课程标准（2017年版2020年修订）》（下文简称“新课标”）指出：要将数学文化融入数学教学活动中. 通过教学中渗透数学文化，让学生了解数学的发展历程，认识数学在科学技术和人类社会发展中所起的重要作用，引导学生认识和感悟数学的文化价值，树立文化自信，提升人文素养和数学核心素养[1]. 2019年普通高等学校招生全国统一考试大纲（数学）在“个性品质要求”中提到：“要求考生具有一定的数学视野，认识数学的科学价值和人文价值，崇尚数学的理性精神，形成审慎的思维习惯，体会数学的美学意义.”然而，对于数学文化内涵的界定，并没有达成共识. 可以说，凡与数学有关的一切事物都可以归为数学文化的范畴. 新课标给出的定义是：“数学文化是指数学的思想、精神、语言、方法、观点，以及它们的形成和发展;还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动.”[1]

近年来，以数学文化作为试题背景已成为高考命题的新亮点、新趋势，数学文化试题具有其他数学试题难以比拟的文化价值与教育价值，它所具有的教育意义和教育价值超越了试题本身. “数学文化作为数学和人类文化的重要组成部分，所体现出来的人文价值、社会价值、科学价值、美学价值和应用价值，对学生的数学素养与数学学科核心素养的培养起着重要作用，也是高考试题的重要考查内容.”基于新课标对数学文化的定义，高考数学全国卷一直在积极探索如何将数学文化与高考数学试题相结合，并通过数学试题考查来渗透数学文化. 在命题时，高考数学全国卷努力将数学文化、数学试题与数学学科核心素养三者有机融合，引导学生“会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界”.以数学文化为背景的试题，可以极大地激发学生的学习兴趣，使学生感受到数学知识浓厚的历史文化底蕴，同时引导学生认识和感悟数学的文化价值、社会价值、科学价值、美学价值、应用价值以及人文精神.

高考数学全国卷力争把数学的理性精神，数学家勇于克服困难的顽强精神，重要的数学概念、公式、法则的发生和发展过程，以及数学的广泛应用融合在一起. 在素材的选取上既关注中国古代数学，也兼顾近现代中外数学史与数学文化. 在对数学文化素材的提炼和总结上，充分发掘数学文化的文化价值、社会价值、科学价值、美学价值、应用价值以及人文精神.

研究设计

1. 研究对象

2018—2020年高考数学全国卷包含Ⅰ、Ⅱ、Ⅲ卷，每套试卷均分为文科和理科，三年一共18套试卷.其中，2018—2019年高考数学全国卷Ⅰ适用于安徽、湖北、福建、湖南、山西、河北、江西、广东、河南、山东，全国卷Ⅱ适用于重庆、陕西、甘肃、宁夏、青海、新疆、黑龙江、吉林、辽宁、内蒙古、海南，全国卷Ⅲ适用于云南、广西、贵州、四川、西藏;2020年高考数学全国卷Ⅰ适用于安徽、湖北、福建、湖南、山西、河北、江西、广东、河南，全国卷Ⅱ适用于重庆、陕西、甘肃、宁夏、青海、新疆、黑龙江、吉林、辽宁、内蒙古，全国卷Ⅲ适用于云南、广西、贵州、四川、西藏.

全国卷是由教育部考试中心组织命制的、适用于全国大部分省区的高考试卷，具有非常鲜明的特征：考查内容基本覆盖了《考试大纲》要求的内容，遵循了《考试说明》的要求，其命题理念完全符合新课标理念，注重对学生数学学科核心素养的考查;考查内容以高中数学主干知识为主线，重点考查学生对重要的数学概念、定理、方法、思想的理解与应用，强调基础性、综合性和应用性，综合考查学生的数学学科核心素养;以问题情境为载体，考查学生综合运用数学知识解决实际问题的能力;注重数学本质、通性通法，命题源于教材、高于教材;淡化解题技巧，融入数学文化，渗透数学思想方法.

2. 数学文化试题的分类

结合PISA（2021）对数学问题背景[2]的分类与高考数学全国卷中试题涉及的数学文化内容，将数学文化试题划分为数学史、数学与生活、数学与人文艺术、数学与科学，但并不涉及数学思想、数学方法和数学精神等[2]. 对数学与生活、数学与人文艺术、数学与科学的详细划分见表1[2].

研究结果与分析

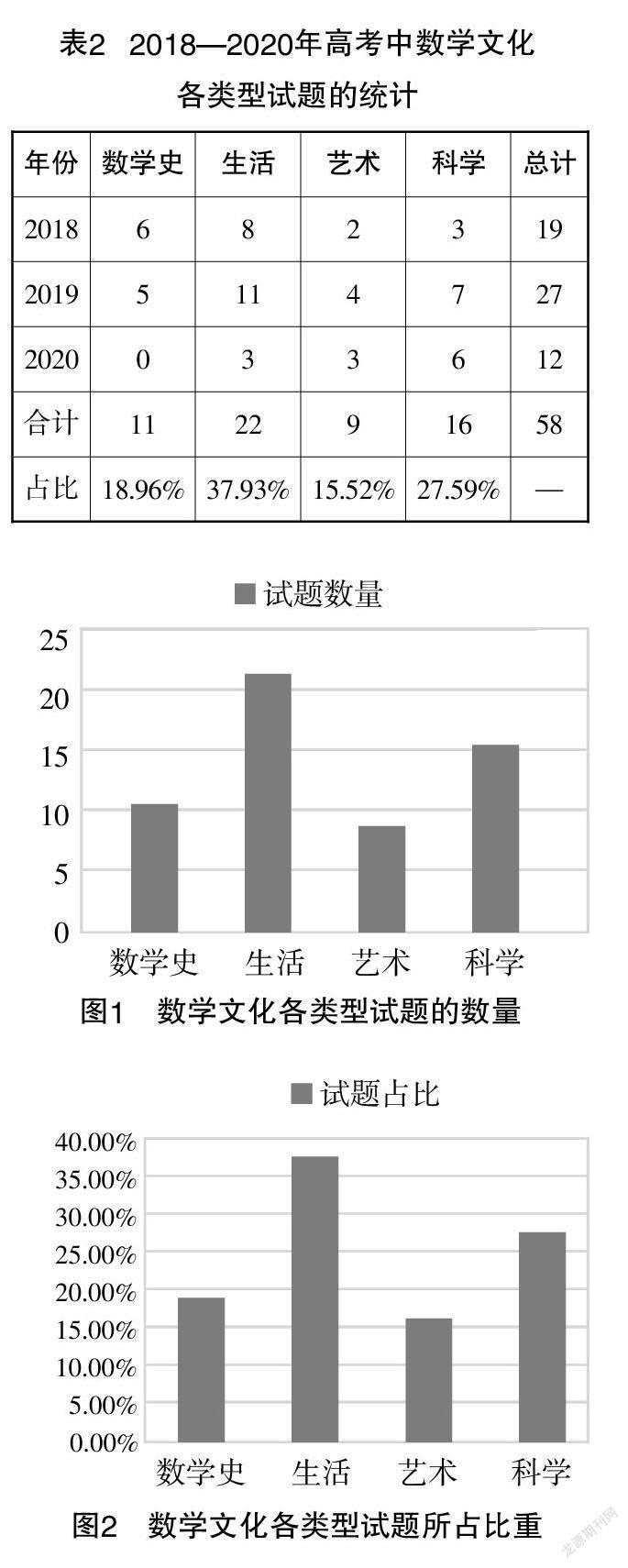
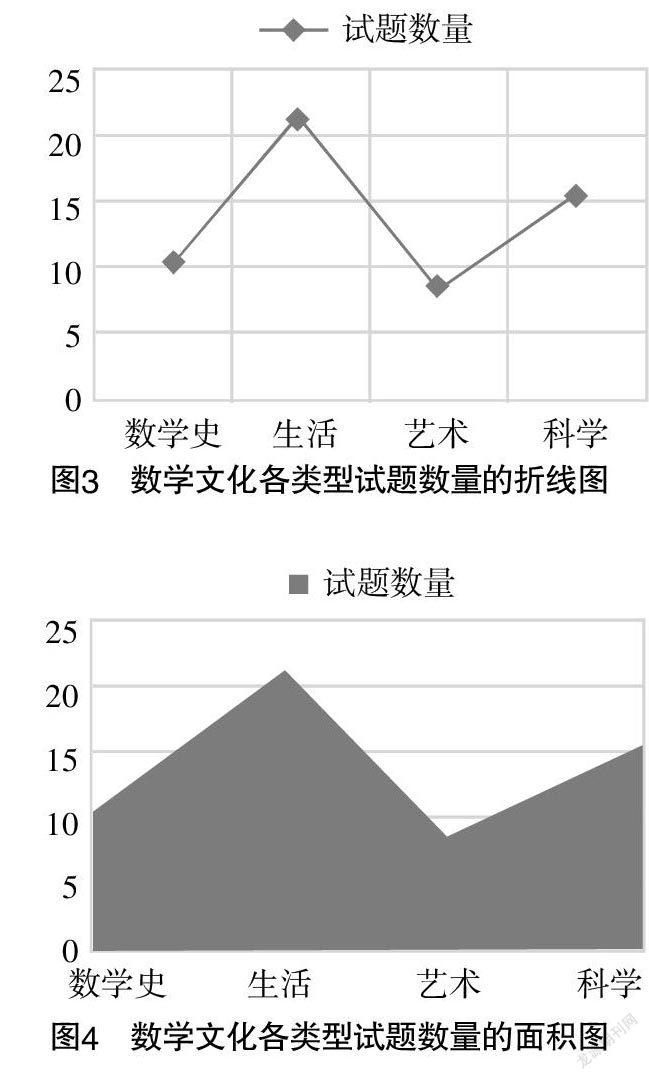
按照上述的分析框架，对2018—2020年18套高考数学全国卷中共计414道试题进行了统计分析，得到了2018—2020年18套高考数学全国卷中数学史、数学与生活（下文简称“生活”）、数学与科学（下文简称“科学”）、数学与人文艺术（下文简称“艺术”）等各数学文化类型试题的数量以及所占比重，结果如表2、图1、图2所示.

由表2可知，2018—2020年，3年高考的数学文化试题数量较少，仅有58道，占试题总量的14.01%. 从题目类型来看，包括了选择题、填空题、计算题和证明题，涵盖了高考数学试题所有的题目类型. 从18套高考数学试卷在数学史、生活、艺术、科学四个方面来看，在生活方面的试题最多，在艺术方面的试题最少. 从数学文化试题涉及的数学知识领域来看，在“统计与概率”领域的试题最多，其次是“代数与几何”領域. 2018—2020年高考数学全国卷中的数学文化试题主要集中在“统计与概率”领域. 究其原因，一方面，“统计与概率”是数学课程改革的重点关注领域：概率是研究随机现象的，为人们从不确定性的角度认识客观世界提供了重要的思维模式和解决问题的方法;统计则是要求学生能对收集的数据进行整理和分析，作出科学合理的决策. 另一方面，从数学应用的角度来看，“统计与概率”的内容与数学课程标准大力强调“应用数学知识来解决实际问题”相契合，这部分内容与学生的实际生活相结合得较紧密. 命题者常常从现实生活或学生不太熟悉的科学情境中提取材料、设置问题，综合考查学生分析和解决实际问题的能力.如2019年高考数学全国卷Ⅰ（理科）第21题，以概率题目为压轴题，背景新颖，题目字数多，阅读量很大，既考查了概率的基础知识和概率的思想方法，又和数列联系起来，综合性极强. 充分体现了数学学科核心素养立意的命题导向.

由图3可知，18套高考数学全国卷在数学史、生活、艺术、科学四个方面的试题数量大致呈斜“N”字形. 在艺术方面的试题最少，在生活方面的试题最多，这在图4中表现得更加明显. 可以看出，高考数学文化试题主要集中在生活、科学两个方面.

为更加清楚2018—2020年高考数学全国卷试题弘扬数学文化的程度，下面从数学文化试题的每个维度进行分析.

1. 以数学史为背景的试题

数学史融入高考数学试题是数学文化的重要体现，可以引导中学数学教学. HPM的实践研究表明，数学史具有激发学生的学习兴趣、增加学习动机、帮助学生理解重要的数学概念等教育价值;而且，还可以通过数学史进行数学学科德育，实现立德树人的根本任务.

数学史融入高考数学试题主要有附加式、复制式、顺应式和重构式四种方式[3]. 从试题中数学史的运用情况来看，以复制式和顺应式为主，运用水平较高. 通过对2018—2020年高考数学全国卷试题的统计分析，可以发现：第一，从题型来看，有选择题、填空题、解答题和证明题;第二，从史料涉及领域来看，涉及代数、不等式、解析几何、立体几何和概率等. 数学史方面的试题的命制来源有三种：①以数学史中著名的问题或定理为背景;②以中国古今数学家的研究成果为背景;③以国外古今数学家的研究成果为背景.

比如，2018年高考数学全国卷Ⅰ（理科）第10题，以古希腊数学家希波克拉底（Hippocrates of Chios，公元前5世纪中期）研究的“化圆为方”内容为背景命制考题，属于“以数学史中著名的问题或定理为背景”的试题，考查几何概型相关知识. 2018年高考数学全国卷Ⅱ（理科）第8题，以哥德巴赫猜想为载体，考查古典概率的计算，这是以附加的方式将数学史融入试题. 2019年高考数学全国卷Ⅰ（文理科）第23题，以均值不等式和柯西不等式为命题背景，考查不等式的证明，属于“以数学史中著名的问题或定理为背景”的试题.

再如，2019年高考数学全国卷Ⅲ（文理科）第21题，以“阿基米德方法”（The Method of Archimedes）和“抛物线图形求积法”（Quadrature of the Parabola）中的相关内容为背景命制考题，属于“以国外古今数学家的研究成果为背景”的试题，考查直线与抛物线的位置关系、直线方程、重心性质、函数最值、弦长公式以及三角形面积等知识，综合考查学生分析和解决问题的能力，同时考查学生数学建模、逻辑推理、数学运算等数学学科核心素养，试题背景的意义与价值已超出了试题本身，将数学的理性精神表现得淋漓尽致. 而且，通过考察历年的高考数学试题，发现“阿基米德方法”中的“抛物弓形面积”是一个命题热点，几乎每年都有以此为背景的考题：江西卷第22题（2005年），全国卷Ⅱ第21题（2006年），江苏卷（理科）第19题（2007年），山东卷第22题（2008年），江西卷第21题（2008年），辽宁卷第20题（2013年），浙江卷第21题（2018年），浙江卷第21题（2019年），等等. 人教A版选修2-1第二章“圆锥曲线与方程”的复习参考题B组第3题与此考题类似.

2. 融数学于人类生活，用数学思维分析实际问题

随着科学研究的发展和进步，数学概念与方法空前广泛地渗透到数学之外的其他学科领域和我们的生活. 正如苏联一位数学家所言，“当今世界不仅仅是科学在数学化，而且绝大多数实践活动也在数学化……我们的时代就是知识数学化的时代.”所谓数学化，就是运用数学思想和方法分析、研究客观世界的种种现象并加以组织的过程. 数学化过程就是从一个具体的情境问题出发，从中提炼数学模型，由实际问题转化到数学问题，由具体问题转化到抽象概念，再由数学概念、公式、法则的再发现转化到具体应用.

新课标中也大力强调数学的应用：“数学的应用已经渗透到现代社会及人们日常生活的各个方面.”通过数学的眼光来观察世界，运用数学的语言来表达世界，运用数学的思想方法来解决实际问题，是数学文化考查的一个重点. 设置这类问题不仅能培养和增强学生的数学应用意识，还能拓宽学生的视野.

将数学文化融入考题时，高考数学全国卷注重考题与背景的有机结合，以不可分离的方式呈现数学文化. 比如，2018年高考数学全国卷Ⅰ（文科）第3题，以我国新农村建设前后农民的经济收入的构成比例为背景，考查学生对统计图表所表达的含义的理解，是一道极富时代气息的试题.要求学生能够从统计图表中提取相关信息，运用所学的统计知识来解决生活中的实际问题，体现了数学的广泛应用性;题目难度不大，但背景新颖，可以极大地激发学生的兴趣，体现了“数学来源于现实，存在于现实，并应用于现实”.再如，2018年高考数学全国卷Ⅱ（文科）第5题，此题以学生参加社区服务为背景，很是贴近学生的生活实际;试题难度不大，可以较好地培养学生的数学应用意识. 2018年高考数学全国卷Ⅲ（理科）第8题，此题以移动支付为背景，需要学生建立相应的数学模型来解决：只要学生能够抽象出题设所蕴含的数学模型，基本就可以解答，考查学生数学抽象、数学建模、数学运算、逻辑推理等数学学科核心素养;在模型分析的过程中，培养学生的数学建模意识，帮助学生积累从具体到一般的数学活动经验.

3. 奠基科學技术，用理性精神服务科学

数学是自然科学的基础与工具，并且在自然科学、社会科学、人文科学等的发展中发挥着越来越大的作用，“随着计算机科学、人工智能的迅猛发展……使得数学的研究领域和应用领域得到极大拓展”，可以说，数学打上了人类各个文化发展阶段的烙印. 正如华罗庚先生所言：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学.”

高考数学全国卷在科学方面的试题较多，仅次于生活方面的试题，占数学文化试题总数量的27.59%;主要涉及医学、农业、天文、工业生产等. 在试题的设计中，注重数学文化与数学问题的有机结合，充分体现了数学是刻画自然规律和社会规律的科学语言和得力工具.

比如，2018年高考数学全国卷Ⅲ（理科）第18题，此题通过茎叶图提供数据信息，要求学生从统计图表中读取信息，考查学生的数据分析素养和应用数学知识解决实际问题的能力. 再如，2019年高考数学全国卷Ⅲ（文理科）第16题，以3D打印技术为背景，背景新颖，极富时代特色，难度不大，主要考查学生的直观想象能力和数学建模能力，充分体现了数学学科核心素养立意的命题导向.

这类试题要求学生在面对具有现实生活背景的实际问题时，能运用数学知识和经验，将实际问题“数学化”：首先将实际问题简化后转化为数学问题，然后进一步符号化处理数学问题并解决问题，最后是回顾、总结和分析已经完成的数学化过程.以数学核心素养立意的试题不仅注意数学分支之间的联系，还注重强调数学的应用性，注重培养学科探究能力.

4. 与艺术联姻，融数学于人类文化

统计表明，2018—2020年高考数学全国卷在艺术方面的考题命制较薄弱，只有9道试题，占数学文化试题总数量的15.52%.

命制数学文化試题时，要找到背景知识和数学学科知识的恰当结合，把人类优秀文化融入试题中，使得学生通过数学运算与数学推理等过程更加深入地理解数学文化，同时感受到数学对推动人类发展所起的巨大作用，这是高考数学全国卷一直秉承的命题立意和导向. 命制数学文化试题时，在深入了解试题背景材料所蕴含的传统文化的前提下，力求在试题呈现和能力考查上突出体现数学文化的核心. 考查的重点是数学的必备知识、关键能力和学科素养，引导学生从数学的角度认识文化，思考文化中蕴含的数学问题，感悟文化中的理性精神.

比如，2018年高考数学全国卷Ⅲ（文理科）第3题，以中国古建筑的榫卯结构为背景，考查三视图的相关内容. 首先，给出榫卯结构图，并对其进行简单介绍，引发学生的兴趣，要求学生先通过空间想象得到俯视图，将几何与生产生活巧妙地结合起来，体现了数学的实用价值，与往常的命题方式大不相同. 又如，2020年高考数学全国卷Ⅱ（文科）第3题，以钢琴的原位大三和弦、原位小三和弦为背景，展现了数学与音乐之间的联系. 题目本身并不难，即使对于没有学过乐理的学生，通过仔细阅读题干也可以理解，这样也考查了学生获取信息的能力. 若学生在解题时又可以进一步发掘不变量关系，则可以将题目进一步简化，能更快地解决问题.又如，2019年高考数学全国卷Ⅰ（文理科）第4题，以黄金分割为背景，不仅体现了数学的应用性，还将数学与美育联系了起来. 可以改变学生对数学的固有印象，让学生感受数学的文化魅力，体会数学的美学意义，体现了数学“以文育人”“以文化人”的功能. 再如，2020年高考数学全国卷Ⅰ（文理科）第3题，以古代世界建筑奇迹之一的埃及胡夫金字塔为背景，此题难度不大，但需要将胡夫金字塔与所学习的立体几何知识相结合，把题目中的条件转化为方程，再求解即可，主要考查直观想象和数学运算两种数学学科核心素养.

结束语

《普通高中数学课程标准（2017年版2020年修订）》明确指出：高考命题时，要“强调学生对重要数学概念、定理、方法、思想的理解和应用……注重数学本质、通性通法，淡化解题技巧，融入数学文化”，并且要“选择合适的问题情境来考查数学学科核心素养”. 高考作为中等教育进入高等教育的一个必经环节，要通过试题来达到“以文育人”“以文化人”的教育功能. 数学文化试题命制需要进一步挖掘数学文化内在的精髓，让学生在解决数学问题时了解数学的发展历程，感受试题背后的数学文化，感悟数学的文化价值，在潜移默化中渗透数学的理性精神. 同时，试题中融入数学文化，要注意数学文化的融入方式（尽量避免点缀、附加的方式），将数学文化深入到试题本身，尽可能做到试题与数学文化不可分离，这样才能更好地突出数学文化的价值.

总之，将数学文化融入试题既要注重体现数学的文化价值、科学价值、应用价值、社会价值以及教育价值，更要注重数学文化与试题的深度融合，避免点缀式、附加式的浅层次融入方式. 试题中融入数学文化要注意数学文化所表述的事件、人物、问题等元素和数学试题之间的联系性，重视数学文化的工具性功能和目标性功能[3]. 这样才能更好地体现数学文化的教育价值，促进数学文化融入中小学数学的课堂教学，形成良性循环.

参考文献：

[1]  中华人民共和国教育部. 普通高中数学课程标准（2017年版）[S]. 北京：人民教育出版社，2018.

[2]  覃淋，李秀萍. 数学核心素养及其特征分析[J]. 中学数学研究，2019（03）：1-5.

[3]  覃淋. 我国高中数学教材的数学史的分析与思考[J]. 教育导刊，2020（02）：71-79.

3875501908253