任意直四边形复合材料层合板振动特性研究

2022-03-19胡双卫钟锐秦斌王青山

哈尔滨工程大学学报 2022年3期

胡双卫，钟锐，秦斌，王青山

(1.中南大学高性能复杂制造国家重点实验室，湖南长沙 410083； 2.中南大学交通运输工程学院，湖南长沙 410083)

任意直四边形复合材料层合板由具有不同力学性能的材料复合而成，它结合了这些组分材料的优良性能，因而被大量用于航空航天、水下航行器、海洋平台等工程领域。在它们实际应用过程中，这类结构往往受到复杂外在的边界约束条件，导致其振动特性异常复杂，研究其在不同边界下任意直四边形复合材料层合板的振动特性对于其工程应用具有一定的科学价值。

研究人员针对板结构振动特性研究提出了一系列数值计算方法，如改进傅里叶级数法[1-3]、微分求积法[4-5]、有限元法[6-8]等。Nie等[1]采用傅里叶级数表示层合板的横向振动，分析了任意直边四边形层合板的自由振动问题。Shi等[2-3]利用改进的傅里叶级数法研究了任意直边四边形板的自由振动特性。Malekzadeh等[4]利用了微分求积法作为一种高效、精确的数值工具对空间导数进行离散，分析了任意直边四边形功能梯度板在热环境下的自由振动。Shu等[5]提出了一种将微分求积法应用于任意四边形板的自由振动分析方法。黄志诚等[6]运用有限元法和试验验证研究了黏弹夹芯板的振动特性。梁宁等[7]利用有限元仿真分析研究了蜂窝纸板的振动传递特性。王迪等[8]利用能量有限元法研究了损伤板结构的振动特性。除了上述方法外，武兰河[9]基于Reissner-Mindlin理论，引入五次样条函数构造试函数，分析了任意四边形厚板的自由振动问题。Semnani等[10]将二维微分变换法(2D-DTM)推广到任意变厚度薄板自由振动的研究中。Magnette等[11]提出了一种离散奇异卷积(discrete singular convolution,DSC)方法，用于任意直边四边形板的振动、屈曲和静力分析。综合文献可以发现，研究人员利用里兹法、改进傅里叶级数法等数值方法分析任意四边形板的振动特性时，需先通过等参变换，将不规则求解域转换为规则的矩形求解域，这种求解方式缺乏灵活性，且增大了建模程序的复杂性；有限元法虽然成为应用广泛的数值方法，但是该方法依托于网格单元，网格自适应性能较差，在处理复杂几何结构的问题时，网格划分显得十分繁琐。另外，现有的关于任意四边形的振动研究多集中于均质各向同性结构，很少涉及复合材料层合四边形板方面的研究。

无网格法最初由Lucy等[12]在研究天体物理学非对称现象时提出。这种数值方法基于节点近似，无需划分网格，因而对于复杂结构动力学问题具有很好的自适应分析能力。彭林欣等[13-14]使用移动最小二乘近似(moving least squares, MLS)各无网格节点的位移场，求解了加肋板的自由振动特性。陈富军等[15]针对层合板，结合局部移动Kriging插值法与一阶剪切变形理论建立了分析其自由振动的数学模型。陈莘莘等[16]结合自然邻接点彼得诺夫-伽辽金法分析了复合材料层合板的自由振动。Zhu等[17]对功能梯度板进行自由振动分析时，使用了Kriging无网格法构造形函数，并与一阶剪切变形理论结合，建立自由振动特征方程。

本文将无网格法应用到任意直四边形复合材料层合板的振动特性分析，运用MLS近似离散节点的位移场及其导数，并通过节点位移近似函数离散结构微分方程，同时结合边界离散方程建立结构的振动求解模型。通过计算结果的对比分析，验证本方法的正确性，进而研究边界约束、材料的杨氏模量比和结构特性参数对任意直四边形复合材料层合板振动特性的影响。

1 任意直四边形板振动模型建立

1.1 模型描述

如图1所示，几何坐标系(X，Y，Z)建立在直四边形板的几何中面上，直四边形板的四条边分别为a，b，c，d，AB与AD的夹角为α，CD与AD的夹角为β，层合板的厚度为h，其具体的几何平面图如图2所示。图1中U、V、W分别代表参考面上任意一点在X、Y、Z方向上的位移。此外本模型在4条边上引入3组线性约束弹簧ku、kv、kw和2组转角约束弹簧kx、ky，改变弹簧的刚度可模拟不同的边界约束条件。

图1 任意直四边形复合材料层合板的几何模型Fig.1 The geometric model of arbitrary straight quadrilateral plate

1.2 移动最小二乘法

本文使用MLS近似来构造形函数，函数u(x)在问题域Ω内的近似函数uh(x)的一般形式可以写为[18]：

(1)

式中：p(x)是二次完备多项式基函数，p(x)=[1xyx2xyy2]T；m是基函数的个数；a(x)是近似函数的系数向量，可以根据加权最小二乘法来确定：

(2)

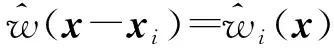
令∂γ/∂a=0，可得：

A(x)·a(x)=C(x)·us

(3)

其中：

(4)

(5)

us=[u1u2…un]T

(6)

将式(3)代入式(1)中即可得到u(x)的近似函数：

uh(x)=p(x)T·A-1(x)·C(x)·us=Φ(x)T·us

(7)

1.3 控制方程

根据一阶剪切变形理论(first order shear deformation theory, FSDT)，任意层合四边形板的3个位移分量可表示为：

(8)

式中：u0、v0、w0分别为板结构中面上沿X、Y、Z方向上的位移分量；φx、φy为转角位移。

板结构的应变-位移关系为：

(9)

任意直四边形复合材料层合板本构方程为：

N=Dijklε

(10)

其中：

(11)

(12)

(13)

式中：A3×3为拉伸刚度矩阵；B3×3为耦合刚度矩阵；D3×3为弯曲刚度矩阵；As2×2为剪切刚度矩阵。以上矩阵中的各元素分别为：

(14)

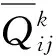
任意直四边形复合材料层合板的平衡方程[20]：

(15)

将式(9)、(10)代入式(15)得：

(16)

式中：k为5×5的刚度矩阵；m为5×5的质量矩阵。

(k-ω2m)u=0

(17)

1.4 控制方程离散化

将任意直四边形复合材料层合板在几何中面上，用M个节点离散，对于层合板内任意一个节点xi，其近似位移为：

u(xi)≈uh(x)=φ(xi)T·us

(18)

式中：us=[u1u2…ui…un]T表示xi支撑域内所有节点的广义位移向量；n表示节点xi的支持域内的节点数，其中ui=[uiviwiφxiφyi]T表示节点xi处的位移向量，此时us为5n×1的矩阵，φ(xi)为5n×5的形函数矩阵，可表示为：

(19)

式中：I为5阶单位矩阵；φi为节点xi处的形函数。

将式(18)代入自由振动控制方程(17)，得：

(kI-ω2mI)us=0

(20)

式中：kI=kφT;mI=mφT。

类似地，建立问题域内所有的节点离散方程，然后将它们组合在一起，得到整个系统的离散方程：

(K-ω2M)Us=0

(21)

式中：K为整体刚度矩阵；M为整体质量矩阵；Us为整体的位移矩阵。

1.5 边界条件离散化

由于边界上要引入人工虚拟弹簧技术模拟边界条件，因此边界条件需要另行离散。系统的边界条件可参考文献[21]，这里以x=0边界为例，进行边界离散说明：

cx0N-kx0u=0

(22)

式中：cx0为系数矩阵；kx0为边界刚度矩阵。

将式(9)、(10)、(20)代入式(22),可得x=0边界的离散方程：

(cx0DijklL2-kx0)Us=0

(23)

同理可得其余3个边界条件的离散方程。

对式(21)、(23)使用子空间迭代法，可以求出任意直四边形复合材料层合板的自由振动频率ω和层合板内部与边界的位移向量Us。

2 数值结果与分析

为验证方法的准确性，下面将给出一些任意直四边形层合板的数值算例研究。如无特别陈述，层合板结构的几何参数和材料属性设定如下：a=1 m，b=0.8 m，c=0.7 m，α=70°，β=75°，h=0.1 m；E2=10 GPa，E1=40E2，G12=G13=0.6E2，G23=0.5E2，μ=0.25，ρ=1 450 kg/m3，铺层设置为[0/45°/0]。特别地，本文使用无网格法建立的自由振动模型，同样适用于各向同性任意直四边形板的自由振动特性研究。实质上各向同性板可作为层合板的特殊案例，即当μ12=μ21=μ，E1=E2=E，G12=G13=G23=E/(2+2μ)，铺设角θ= 0°时，复合材料层合板将退化为各向同性板，此时层合结构的振动分析模型将转变为均质的任意直四边形板的振动模型。另外，在本节中采用的无量纲频率定义为：

(24)

2.1 有效性与收敛性验证

从上节中理论推导可知，边界刚度对于计算结果具有较大影响。图2给出了无量纲频率参数随边界刚度变化的曲线。可以看出，当边界弹簧刚度小于107N/m时，层合板的无量纲固有频率基本不变；当边界弹簧刚度在107～1011N/m变化时，频率参数近似线性变化，可将其定义为弹性支撑边界；当边界弹簧刚度大于1011N/m时，板的无量纲固有频率达到收敛状态，可作为刚性边界条件。从图中还可以看出kx、ky对板的无量纲固有频率影响较小。根据上述分析，本文所涉及各种边界约束如表1所示。

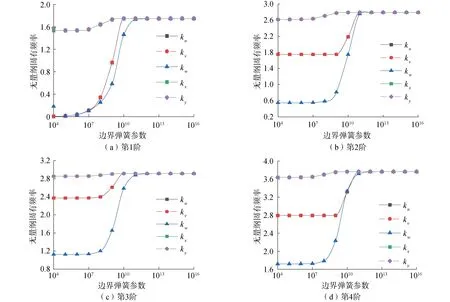
图2 层合板边界弹簧刚度收敛曲线Fig.2 Convergence curves of boundary spring stiffness of laminated plate

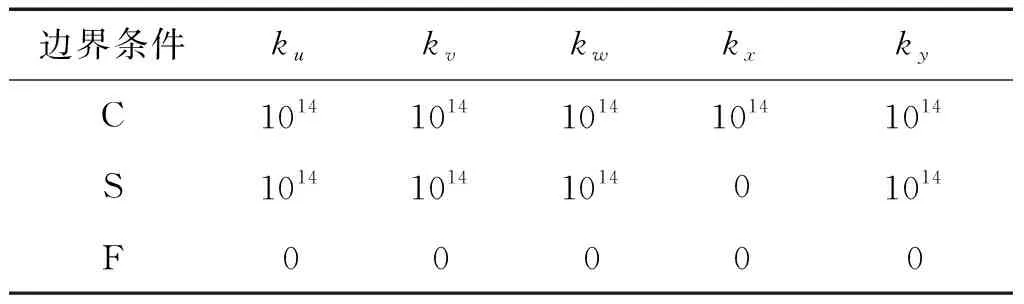
表1 不同边界条件下对应的弹簧刚度

下面将给出所建模型的有效性分析。本算例的几何尺寸设置为a=b=c=d=1 m，α=β=90°，铺层角度为[45°/-45°]。表2给出了任意四边形层合板的前4阶无量纲频率参数对比。对比结果表明，无网格法所得计算结果与文献[20]参考解具有较好的一致性，两者之间的最大误差为3.71%，这说明无网格法适用于复合材料层合四边形板的振动特性预测。

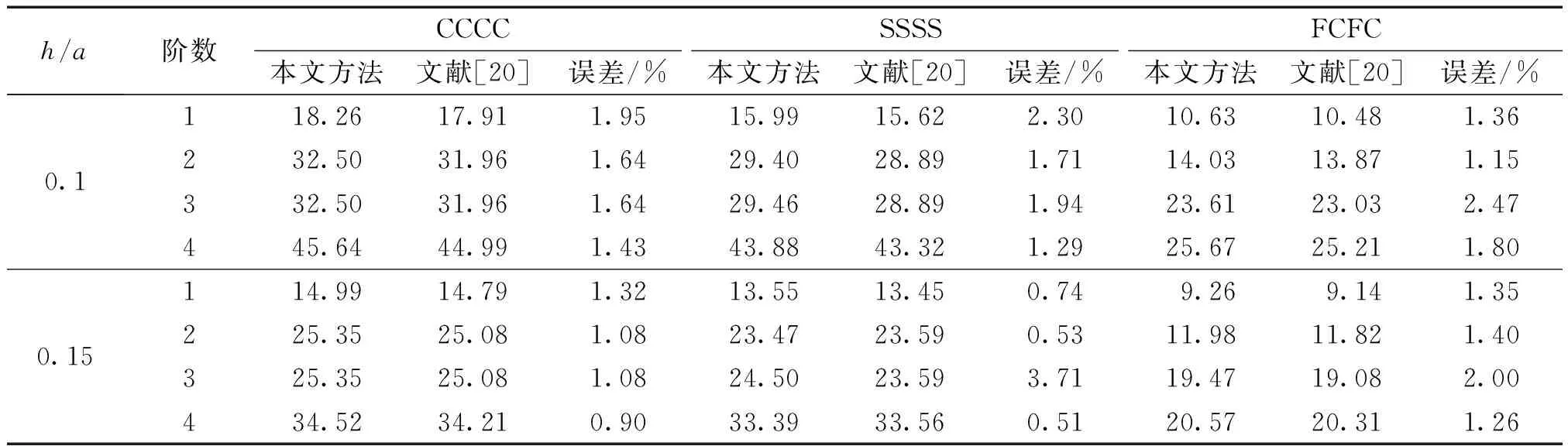
表2 任意直四边形复合材料层合板在不同边界条件下前4阶无量纲固有频率Ω对比

2.2 自由振动算例分析

图3研究了杨氏模量比E1/E2对任意直四边形复合材料层合板的无量纲频率的影响，杨氏模量比是表征层合板各向异性程度的量。在该算例中，层合板的杨氏模量比在1～25变化，计算步长设为1。从图中可以看出不论是C-C-C-C边界，还是S-S-S-S边界条件，层合板的无量纲固有频率随杨氏模量比的增大而增大，虽然在这2个边界条件下，层合板的无量纲频率参数随弹性模量比的增长趋势相同，但在S-S-S-S边界条件下，无量纲频率参数的增长速度要比C-C-C-C边界条件下的要较快，这表明层合板的频率参数对杨氏模量的变化更为敏感。

图3 层合板无量纲频率参数随杨氏模量比E1/E2的变化Fig.3 Change of non-dimensional frequencies of laminated plate according 1 to the increase of Yong′s modulus ratio E1/E2

图4研究了3种纤维铺设方式对任意直四边形层合板的振动特性的影响，这3种铺设方式分别为[0,θ, 0]、[θ, -θ]和[θ, 0,θ]。在该图中θ的变化范围为[5°, 175°]，变化步长为5°。观察图4可以发现对于[0,θ, 0]，在C-C-C-C边界条件下，直四边形板的频率参数在θ=90°达到峰值，振动特性近似关于90°对称，而对于SSSS边界条件，频率参数的峰值在θ=95°时获得，且无量纲固有频率关于θ=95°对称。对于[θ, 0,θ]铺设方式，无论哪种被讨论的边界，频率参数均在θ=90°时达到峰值，但图像并不关于θ=90°对称。出现上述现象的原因是本算例讨论的任意直四边形板在几何上不对称。但对于[θ, -θ]的铺设方式，在四边形板的厚度方向呈现对称性，因此图像关于θ=90°对称。同时还可以发现对于2种边界条件，结构的无量纲固有频率表现出来的变化趋势是一致的，但峰值出现的位置存在差异，对于C-C-C-C边界，无量纲固有频率在θ=90°达到峰值，而S-S-S-S边界，θ=45°和θ=135°时，频率参数达到峰值，这说明边界弹簧刚度，会改变结构的振动特性。

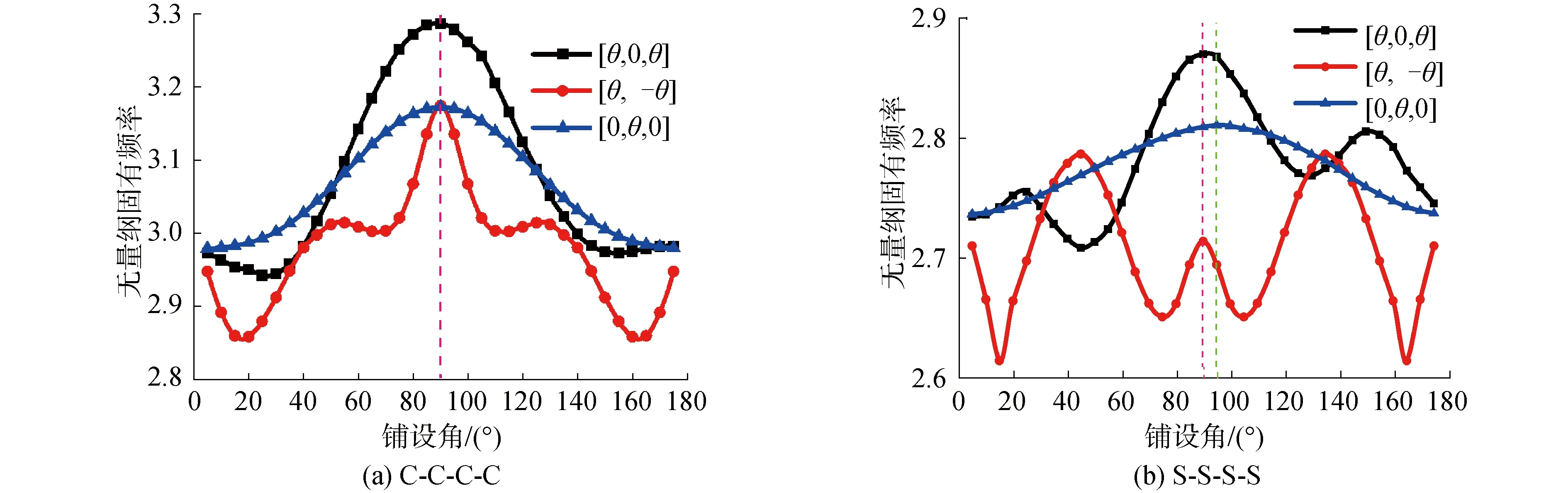
图4 任意直四边形层合板的纤维铺设角对其振动特性的影响Fig.4 Influence of fiber laying angle on vibration characteristics of any straight quadrilateral laminates

图5研究了铺设层数λ对层合板前三阶无量纲固有频率的影响规律。考虑的边界条件为四边固支和对边固支，对边固支是指将图1(b)中的AD边与CB边固定，其余2条边处于自由状态。本案例纤维铺设方法是[0, 90°]λ，保持层合板的厚度不变，层数λ由1到10逐步增加。由图5可知，随着铺设层数的增加，层合板的无量纲固有频率呈锯齿状上升。说明层合板的自由振动特性与层合板纤维层数的奇偶有关。