四鹰头周向均布波浪能浮标模型试验
2022-03-19吴明东盛松伟张亚群姜家强
吴明东, 盛松伟, 张亚群, 姜家强
(1.中国科学院广州能源研究所,广东 广州 510640; 2.中国科学院可再生能源重点实验室,广东 广州 510640; 3.南方海洋科学与工程广东省实验室(广州),广东 广州 510640; 4.中国科学院大学, 北京 100049)
利用海洋能解决观测浮标的电力供给问题,实现海能海用、原位供电,将是未来海洋观测浮标高效、经济且可持续获能方案,可支撑海洋观测活动大功率、批量化发展[1-2]。海洋中蕴藏丰富的能源,其中波浪能分布范围广、适用范围大,利于浮标广泛获能。但波浪运动具有明显的随机性和分散性,在环境恶劣的海洋中收集和转换波浪能供浮标使用,需开发高效且可靠的能量转换装置。
有关波浪能的能量转换技术,国内外都有相关研究。盛松伟等[3-4]利用振荡浮子技术研发的鹰式系列装置,配备了自主研发的液压式能量转换系统,并对发电系统进行了优化;Antnio等[5-7]对先进的振荡水柱技术进行了阐述、对比,结合动力学对振荡水柱式浮标波浪能转换装置进行了优化;吴必军等[8-9]对后弯管技术进行了优化,通过改进装置的外型等要素提高转换效率。
本文以海洋观测用波浪能浮标模型为研究对象,在三维水池中测量不同波况、不同负载下模型的俘获总效率、4个鹰头的做功占比、鹰头的推力和标体的运动倾角。通过试验和分析,验证了设计的合理性,总结了可进一步优化的方向,试验结果将用于实海况装置的关键参数推算和装置设计。
1 试验模型、设备及工况设计
1.1 试验模型及安装
模型将2种波浪能转换机构融为一体,以提高装置整体俘获效率,一种为振荡浮子转换机构,另一种为振荡水柱转换机构。振荡浮子式机构设置了4个按圆周均布的鹰式吸波浮子,通过浮体吸收波浪能,鹰式吸波浮子在波浪作用下往复运动推动液压缸顶升重物做功,将波浪能转换为重力势能[10]。振荡水柱式机构是在装置主体内部设置了一个特殊气室,通过气室中波浪水柱的振荡获得能量,将波浪能转换为气体动能。
模型装置由3个部分组成,如图1所示,第1部分为柱状主体,由多个不同直径的圆柱体连接而成,高2.3 m,上部圆柱直径最大0.72 m,该部分结构内设置气室,顶部可安装气动波浪能转换机构,内置气室最大容量54.4 L,喷嘴比近似等于吃水线气道横截面积与上端开口横截面积之比为0.07,3层底盘直径分别为1.2、1.2、2 m,为提高浮标的耐波性,四周焊接围板以增加装置的垂荡阻力;第2部分为安装在上部圆柱四周的2种鹰式吸波浮子,用以对比2种形状浮子的俘获性能,一种侧面为直角阶梯状,另一种侧面为斜角平面,通过铰链与上部圆柱结构连接,鹰式吸波浮体与圆柱上端刚性支架之间安装有液压缸,安装了4个鹰头后的装置最大直径为1.9 m,单个鹰头正面迎波宽度1.2 m,侧面迎波宽度0.5 m;第3部分为锚泊系统,装置腰部连接3条锚链,向外均布,1根6 m锚链沿波浪走向布置于模型后方,2根7 m锚链布置于造波机侧。模型安装位置距离造波机侧36 m,距离浪高仪30 m。

图1 波浪能浮标模型Fig.1 Wave energy buoy model
1.2 试验设施及设备
本文试验在国家海洋技术中心大比尺波浪水槽开展,该水槽长130 m,宽18 m,试验段水深4.5 m,能够产生多种规则波和不规则波,最大造波波高0.6 m,最大造波周期5 s,试验平台离水面高3.5 m。水池示意图如图2所示。

图2 试验波浪水池Fig.2 Waving carriage
试验设备布置如图3(a)所示,包括:波高仪,型号YWH201-A,量程1 m,频率1 kHz,产品自带计算软件可用来实时监测模型前端入射波况;鹰头液压缸,行程200 mm,活塞直径20 mm;蓄能器液压缸,行程600 mm,活塞直径63 mm;位移传感器,量程0~1 000 mm,精度0.5%,用来测量重块顶升高度;风压变送器,型号JX-H260,量程±2 kPa,频率为3 Hz,用来测量气室内外气压差;流量传感器,型号HJTH-D80,量程0~180 N·m3/h,用来测量气室内气体流量;航姿传感器,型号BWD-VG220,量程俯仰-90°~90°,横滚-180°~180°,频率100 Hz,测量标体倾角;拉力传感器,量程0~2 000 N,精度0.5%,测量锚链拉力。

图3 波浪能浮标模型安装示意Fig.3 Installation diagram of wave energy buoy model installation
1.3 工况设计
试验波况设计包括规则波和不规则波,不规则波采用Jonswap谱。浮标目标投放海域为我国南海,实海况波浪周期为4.5~6 s。为研究相对有利于装置能量转换效率的波况,规则波周期选取1.2、1.3、1.4、1.5 s,波高选取100、120、140 mm;不规则波谱峰周期选取1.25、1.5 s,有义波高选取156、187 mm。模型装置推动鹰头液压缸,每个鹰头顶升1根重力式蓄能液压缸,4根蓄能液压缸顶部重块重量相同,选取10~180 kg。单组试验重复3次,采集时间大于20个波浪周期,测得数据取中间值。具体试验参数设计如表1、2所示。

表1 规则波试验工况Table 1 Regular wave test conditions

表2 不规则波试验工况Table 2 Irregular wave test conditions
2 计算方法
试验中,鹰头将俘获的波浪能转换为蓄能液压缸内液体的重力势能和顶升重块的重力势能。因此,振荡浮子的效率为单位时间内系统重力势能增加之和与来波功率的比,计算公式为:
(1)
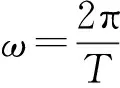
试验中气动装置将俘获的波浪能转换为气体动能。因此,气动装置的效率为单位时间内气室输出的气动功率与来波功率的比,计算公式为:
(2)
式中:ΔP为气室内外气压差,Pa;V为气体流量,L;t2为液面做功时间,s;b在此为柱状主体的迎波宽度,b4=0.72 m。
由式(1)、(2)可得模型整体的转换效率计算公式为:
(3)
式中b为装置的最大迎波宽度,即四鹰头的迎波宽度,b3=1.9 m 。
试验中液压缸顶升重块的加速度较小,对液压缸活塞压强的影响不计,近似为静态压强。管路内鹰头液压缸活塞与蓄能液压缸活塞的压强近似相等,即:
(4)
故单个鹰头推力计算公式为:
(5)
式中:A1、A2分别为鹰头液压缸、蓄能液压缸活塞面积,m2;F为鹰头推力,N。
四鹰头做功单个鹰头占比计算公式为:
(6)
式中h4表示单个鹰头对应液压缸重块升高高度,m。
3 试验曲线与结果
按照设定参数,取鹰头液压缸做功时间20个波浪周期以上,根据式(1)、(2)所得输出功率为单个试验周期内蓄能液压缸所蓄能量、气室输出气体动能与时间的比值,故本试验所得振荡浮子效率和振荡水柱效率都是平均效率。
3.1 试验波况
本试验使用波高仪自带计算软件实时监测模型前端入射波况。工况设计选取的5种规则波的实测波况数据如图4所示,2种不规则波的实测波况数据如图5所示,其中截取时长至少包含20个有效波浪周期。

图4 规则波试验波况Fig.4 Regular wave test conditions

图5 不规则波试验波况Fig.5 Irregular wave test conditions
3.2 转换效率与出力
根据装置实测做功数据和式(1)、(5)得四鹰头总平均效率曲线如图6、7所示。根据计算公式(5)得到不同波况下最优负载对应的鹰头出力分布图,如图8所示。
由图6、7可知,2种形状的鹰头俘获性能相近。最优的规则波况为周期1.4 s、波高120 mm,对应最优负载为60 kg;最优的不规则波况为谱峰周期1.5 s、有义波高187 mm,对应最优负载为50 kg。依据计算公式(1)~(3)得2种最优工况下的四鹰头总效率分别为40%、26%,气动效率为17%、5%,装置总效率为46%、28%(其中气动部分占比13%、7%)。
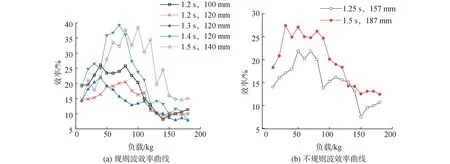
图6 直角鹰头迎波时的效率曲线Fig.6 The efficiency curves of right-angled eagle facing waves

图7 斜角鹰头迎波时的效率曲线Fig.7 The efficiency curves of beveled eagle facing waves
根据图8结合上文可知,最优规则波、不规则波况下的最优负载对应的单个鹰头出力为59.3、49.4 N。

图8 鹰头出力Fig.8 The eagle output
3.3 鹰头做功占比与效率
由图9、10可知,在最优波况、最优负载下,同组试验测得侧面迎波鹰头和正面迎波鹰头的做功占比相近,前者的效率高于后者,注意鹰头的正面迎波宽度为b1=1.2 m,侧面迎波宽度为b2=0.5 m,背面迎波鹰头则做功较少。
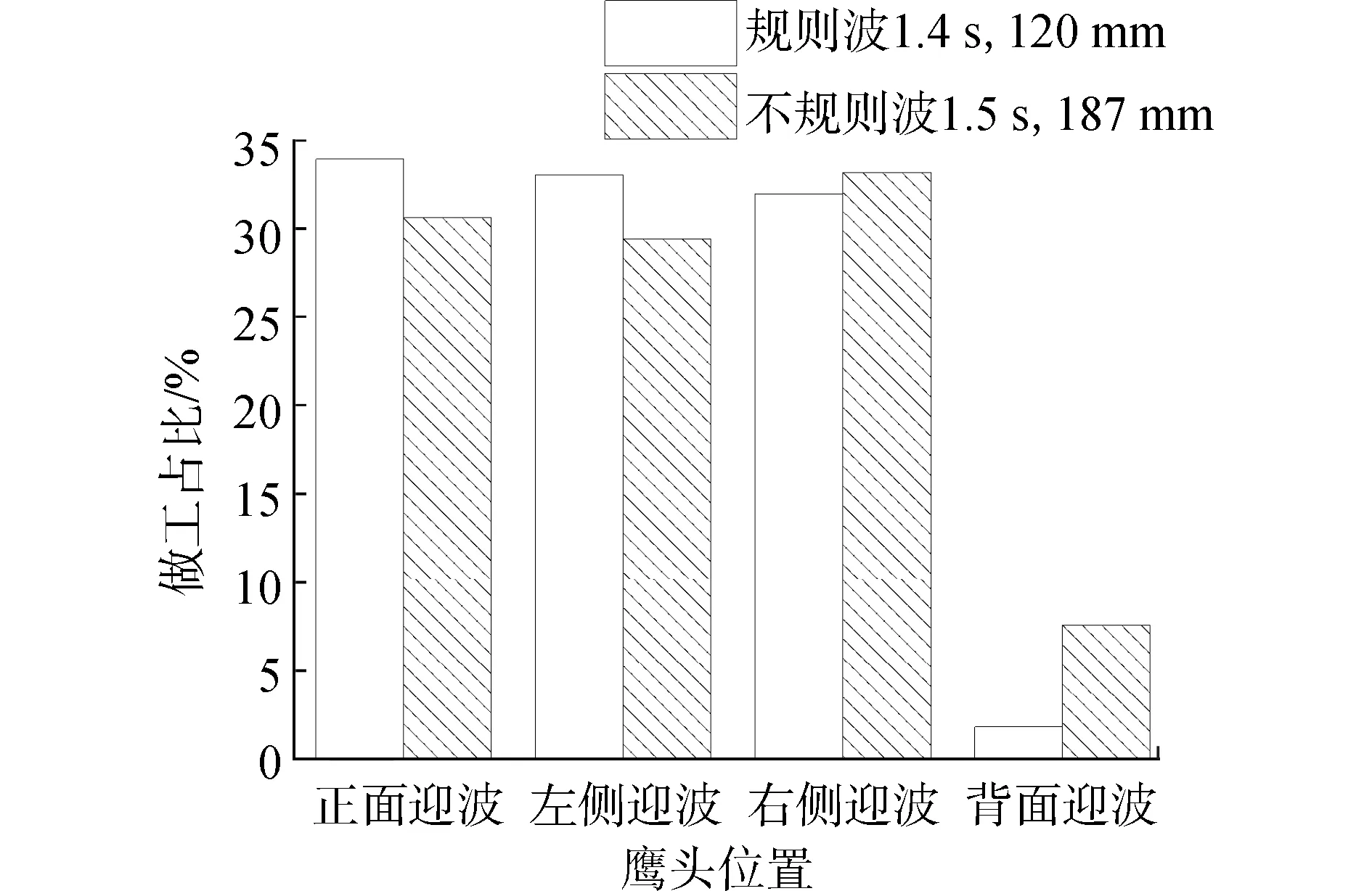
图9 最优波况、最优载时各鹰头做功占比Fig.9 The proportion of work done by each eagle under optimal wave condition and optimal load time

图10 最优波况、最优载时各鹰头效率Fig.10 The efficiency of each eagle under the optimal wave condition and optimal load
根据模型设计尺寸分析,侧面迎波鹰头的浪向长度为1.2 m,正面迎波鹰头的浪向长度为0.5 m,单个周期的波浪在传递过程中对前者做功时间大于后者,是导致侧面迎波鹰头吸收效率更高的主要原因,该结果说明吸波浮子的浪向长度对该浮子的做功能力影响很大,加大吸波浮子的浪向长度可有效提高俘获效率。
3.4 姿态与倾角
通过航姿传感器得到波浪能浮标在波浪中的倾角曲线如图12所示。
在造波起始阶段标体的倾角随着波浪推力的增大同步增大,当波况趋于稳定时,标体的倾角也趋于某一倾角(基准倾角)附近一定范围内振荡。模型试验照片如图11所示。

图11 模型姿态Fig.11 Model posture pictures
由图12可知,在周期1.2 s、波高120 mm和周期1.4 s、波高120 mm 2种波况下,标体纵摇基准倾角分别为6.5°、6.7°,横摇基准倾角分别为2°、3.4°,纵摇倾角受波浪周期影响更大,但2种波况下横摇、纵摇在基准倾角上下振荡的幅度基本不变。
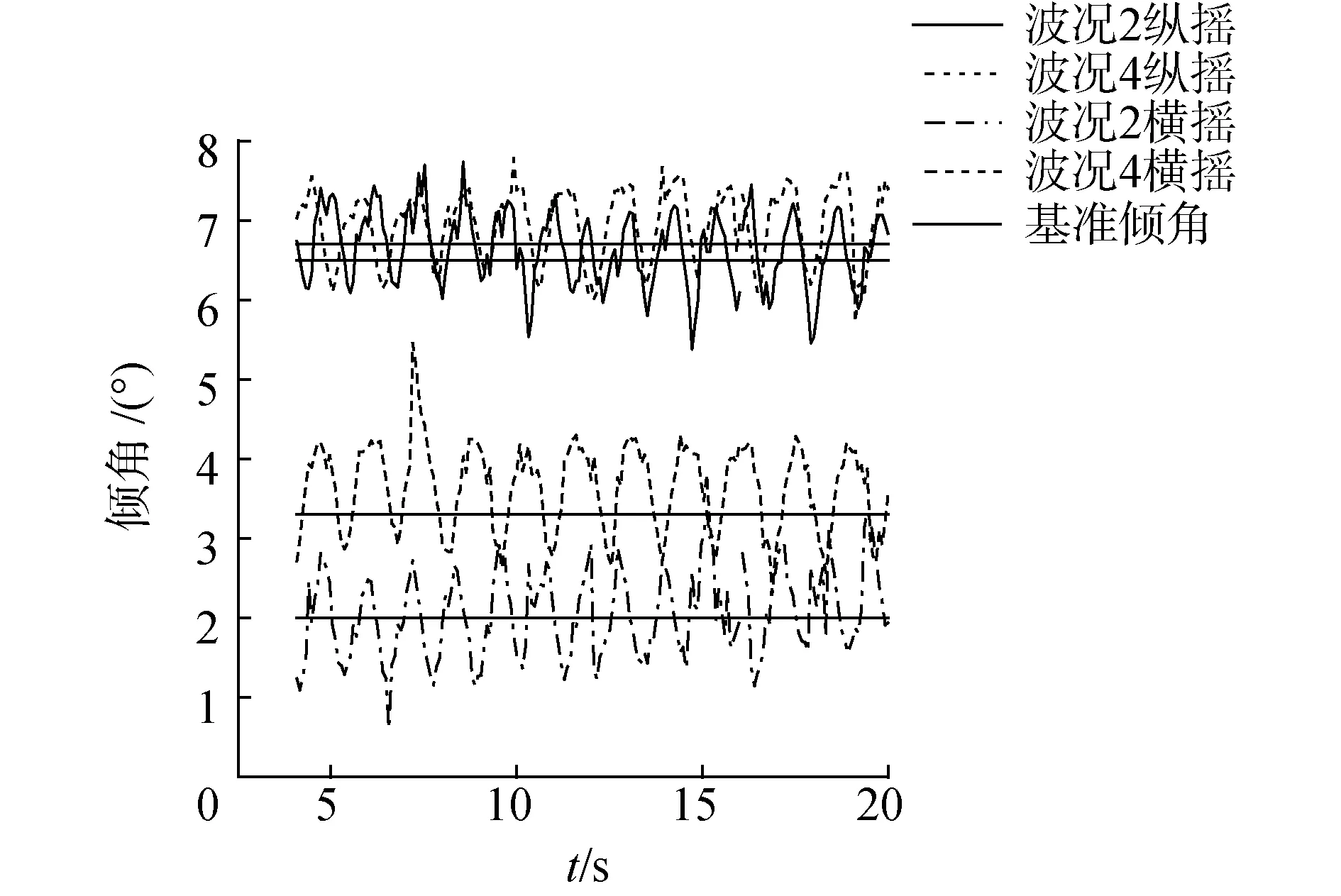
图12 不同波况下标体的倾角Fig.12 The dip angle of the buoy under different wave conditions
4 结论
1)通过模型对比试验,得到规则波相对最优波况为周期1.4 s、波高120 mm,不规则波相对最优波况为谱峰周期1.5 s、有义波高187 mm,对应最优负载分别为60、50 kg。2种波况下模型的最大俘获效率分别为46%、28%。
2)以上2种最优工况下单个鹰头出力分别为59、49 N,下一步将作为后端发电机功率选型的关键参数。
3)试验中安装气动转换机构对整体转换效率的提升不明显,分析原因为大部分入射波被柱状主体前的迎波浮子吸收。
4)通过最优工况下4个鹰头做功占比和转换效率对比,发现正面迎波鹰头的转换效率低于侧面鹰头,分析得到吸波浮子的浪向长度对该浮子的做功影响很大,加大吸波浮子的浪向长度可有效提高俘获效率,该结果为后续进一步优化吸波浮子的外形提供了指导方向,意义重大。
