基于模态陷获能量比的水面水下目标分辨技术

余赟， 刘清宇， 虞飞， 殷敬伟

(1.海军研究院， 北京 100161； 2.哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨 150001)

水面水下目标分辨是水声领域中迫切需要解决的问题，确定声源位于水面还是水下有利于声呐对关键目标的识别和跟踪，尤其是对于缩短反应时间、提高水下目标识别正确率、降低虚警率有重要意义。

水面水下目标分辨技术大致可归类为2种技术途径，一种是基于目标辐射噪声谱特征的水面水下目标分辨技术，该技术途径希望剥离水声信道对目标源特性的影响，由于涉及到水声目标特性，密级较高，在公开文献上报道得少。另一种技术途径是基于目标-声场耦合特性的水面水下目标分辨技术，该技术途径可通过匹配场处理[1]、匹配模处理[2]等估计目标深度，或通过对目标深度相关统计量的分析处理[3-8]实现水面水下目标深度二元分类。

匹配场处理方法[1]是对声源进行深度估计的有效方法之一，该方法利用声传播模型计算拷贝场，然后将测量场和拷贝场进行匹配，然而匹配场测深方法面临环境参数测量不准确、计算量大、耗时长等问题。模态匹配处理方法克服了匹配场处理中计算量大和环境失配的问题，Shang等[2]采用模态匹配的方法对声源深度进行估计，将接收信号经模态滤波后取模与拷贝场中本征函数取模后进行相关运算，获得深度模糊函数，模糊函数峰值对应深度为声源深度估计结果。然而此方法忽略了本征函数的极性，影响了声源深度估计结果的准确性。Nicolas等[9]充分利用模态相位信息，提出了一种本征函数极性估计方法，可以有效估计本征函数的极性，提高了算法估计声源深度的性能。此方法需要较大的阵列孔径，当阵列孔径较小时，估计声源深度的性能下降。Yang[10]基于合成孔径波束形成思想对运动目标激发声场做Hankel变换得到波数谱，根据谱峰位置估计声源深度。此方法对声速分布不敏感，当声速分布失配时，其稳健性优于匹配场和模态匹配的方法，然而当声源运动距离较小时，算法性能下降明显。李鹏等[11]基于波束形成思想提出一种模态分离方法，利用水平阵列实现了对窄带和宽带声源的深度估计，但该方法对阵列孔径和声源方位预估的精确度要求较高。

由于水面水下目标深度二元分类方法对环境失配宽容度高，国内外学者开展了大量研究，此类算法通常具有更高的运算效率和稳健性。Premus[3]提出了模态闪烁指数的概念，并将其用于浅海波导中水面目标和水下目标分辨，模态闪烁指数有其明显的缺陷，它与声源级和距离有关，算法受声源级和距离的影响。安良等[4]对模态闪烁指数进行了修正，修正后的模态闪烁指数仅与声源深度有关，扩展了方法的适用性。李琳[12]将该方法推广到深海波导中水面水下目标分辨问题中，取得了较好效果。Premus等[13]注意到水面和水下目标辐射噪声在各阶模态子空间的能量分布存在差异，引入子空间匹配检测器，提出了一种基于匹配子空间的深度判别方法，并将此方法分别应用于垂直阵列和水平阵列，当阵列孔径较大时，方法性能较好。Conan等[14]提出了一种基于陷获模态能量与总能量比的深度判决方法，将低阶模态能量与全部模态能量的比值作为声源深度判决统计量，此方法在覆盖半水层深度的垂直阵上得到了较好的判决效果，降低了对阵列孔径的要求。郭良浩等[15]将最小方差无失真响应波束形成算法应用于波数谱估计，根据低阶简正波和高阶简正波幅度的差异性实现对水面水下目标分类，方法受声速分布影响较大，环境宽容性有待提高。

本文介绍了温跃层水文波导条件下模态传播特性，给出了反转模态和反射模态能量随深度分布规律，分析了水面目标和水下目标声场中反转模态能量与总能量比值的差异性，基于此物理特性，提出了一种基于模态陷获能量比的水面水下目标分辨方法，最后对算法稳健性进行了仿真验证。

1 模态传播原理

1.1 简正波理论及模态分类

简正波理论下，当接收水听器与声源之间的距离大于几倍海深时，若声源深度为zs，频率为ω，则深度zr、距离r处接收到的单个无指向性点源辐射声场可以表示为有限阶模态和的形式：

(1)

式中：krm为第m阶模态的水平波数；φm为第m阶模态的本征函数。

若引用射线声学中反射和折射的概念，可将简正波分为海面反射-海底反射模态、折射-海面反射模态、折射-海底反射模态、折射-折射模态，第1种模态称为反射模态，后3种模态又被称为反转模态，综上，可将简正波分为反射模态和反转模态2类。反射模态和反转模态具有不同的水平波数分布范围，如图1所示。

图1 反射模态和反转模态的水平波数分布Fig.1 The horizontal wavenumber distribution of reflected modes and refracted modes

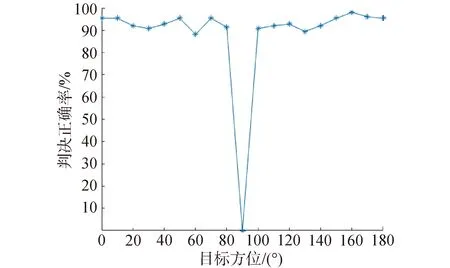
对于反射模态，水平波数满足ω/cseafloor

1.2 温跃层水文波导模态传播特性

浅海温跃层波导条件下，不失一般性，水面目标位于跃层以上深度，水下目标位于跃层内或跃层以下。对于水下目标，小掠射角声线在跃层上边界发生反转，声能量被陷获在跃层以下深度内传播，其声场主要由反转模态主导；而对于水面目标，由于不能激发反转模态，其声场主要由反射模态主导。

典型温跃层声速分布如图2所示，图中20～40 m深度范围存在声速跃变。

图2 温跃层声速分布Fig.2 The sound speed profile with thermocline

图3分别为信号频率300 Hz和信号频率700 Hz时各阶模态的模深度函数分布。信号频率300 Hz时，声场中存在13阶传播模态，其中4阶为反转模态，9阶为反射模态；信号频率700 Hz时，声场中存在30阶传播模态，其中10阶为反转模态，20阶为反射模态。可以看出，声源频率越高，声场中传播模态越多，且反转模态阶数与频率有关。但由图中模深度函数强度分布可以看出，浅处声源不能激发低阶反转模态，而深处声源声场低阶反转模态能量较强，不同频率声源激发的声场均满足这一规律。

2 水面水下目标分辨

2.1 模态能量比

根据上节所述温跃层波导声传播特性，水面目标辐射声场由反射模态主导，水下目标辐射声场由反转模态主导，因此水面目标和水下目标声场中反转模态能量和传播模态能量比值存在差异性，该比值的差异性即为本文所提水面水下目标分辨算法的物理基础。

定义反转模态与传播模态的能量比值为：

(2)

式中：M0为反转模态数；M为传播模态数；am为第m阶模态的幅值。

仿真采用的声速分布如图2所示。图4为接收深度70 m，信号频率300 Hz和信号频率700 Hz时不同距离上能量比Ra随声源深度变化规律，可以看出：当声源位于跃层以上深度(小于20 m)时，能量比Ra趋近于0；当声源位于跃层内深度(20～40 m)时，能量比Ra随深度增加而增加；当声源位于跃层以下深度(大于40 m)且不靠近海底时，能量比Ra接近于1；当声源位于不同距离时，能量比Ra均满足以上规律。

图4 反转模态与传播模态能量比Fig.4 The energy ratio of refracted modes and propagating modes

2.2 空域滤波器设计

为实现从阵列接收信号中分离出反转模态能量和传播模态能量，进而估计反转模态能量与传播模态能量的比值，本节开展波束形成空域滤波器设计。

简正波可以看作一系列平面波的叠加，因此反射模态和传播模态对应不同的波达角范围，即在不同的水平波数范围内，设计2组波束形成空域滤波器，其通带分别对应反转模态波达角范围和传播模态波达角范围，频率300 Hz和频率700 Hz对应的波数响应函数如图5所示，可以看出，通过设计波束形成空域滤波器，可以分别实现反转模态与传播模态的能量估计。

图5 波数响应函数Fig.5 The wavenumber response functions

记通过反转模态空域滤波器得到的波束输出为B1(θs)，通过传播模态空域滤波器得到的波束输出为B2(θs)，则反转模态与传播模态能量比估计值为：

(3)

2.3 判决门限

对于水面目标和水下目标分辨问题，通常分界深度设定为水面以下几米到十几米的深度，假定目标深度为zs，设定的分界深度为zlim，则：

当zs

当zs>zlim时，判定为水下目标。

而由2.1节得到的反转模态与传播模态能量比随声源深度变化规律可以得出，对于水面目标和水下目标判决的分界深度范围，能量比随声源深度单调变化，因此可设定分界深度处的反转模态与传播模态波束输出能量比值为判决门限η，判决门限计算流程如图6所示,其中，r1～rL表示距离采样点。

图6 判决门限计算流程Fig.6 The flow chart of decision threshold setting

通过比较接收信号的能量比估计值Rb与门限η的大小分辨水面目标和水下目标，即：

当Rb<η时，判定为水面目标；

当Rb>η时，判定为水下目标。

3 性能仿真分析

水面目标和水下目标分辨处理流程如图7所示。首先，根据海深、声速剖面、底质类型等海洋环境参数开展声场数值计算，计算不同声源深度下的反转模态和传播模态能量比，根据需要的临界深度确定判决门限；同时，结合声呐工作频段和海洋环境参数设计不同频率下的反转模态空域滤波器和传播模态空域滤波器；再次，阵列接收信号分别通过反转模态和传播模态空域滤波器滤波后进行波束形成，得到反转模态波束输出和传播模态波束输出，并计算反转模态和传播模态能量比；最后将得到的反转模态和传播模态能量比与判决门限比较，判断水面目标或水下目标。

图7 水面目标和水下目标分辨处理流程Fig.7 The flow chart of surface target and underwater target discrimination process

仿真条件如下：采用的声速剖面如图2所示；接收基阵为500元水平直线阵，阵元间距1 m，接收深度为70 m；水面目标深度为7 m，水下目标深度为35 m，均位于接收基阵端射方向，信号频率为300 Hz，目标距离从5 km变化到20 km，距离间隔100 m。

仿真得到水面目标信号和水下目标信号各151组。若设定分界深度为20 m，计算得到能量比判决门限为0.257，处理得到不同距离上水面目标信号及水下目标信号的反转模态/传播模态波束输出能量比值如图8所示。统计可得，水面目标信号判决正确144组，判决正确率为95.4%，水下目标信号判决正确148组，判决正确率为98.0%。

图8 水面目标和水下目标分辨结果Fig.8 The discrimination results of surface target and underwater target

算法在不同仿真条件下的稳健性分析如下。

1)处理频带。

处理信号频带分别为50～100、100～200、200～400、375～750 Hz时，水面目标和水下目标分辨正确率如表1所示。可以看出，随处理频带增宽，水面目标和水下目标的分辨正确率均显著提高，水下目标分辨较水面目标分辨对处理频带选取更加宽容，在几组处理频带下，水下目标分辨正确率均大于90%。

表1 不同处理频带下水面目标和水下目标判决正确率

2)接收深度。

在实际应用中，水下目标分辨具有更重要的意义。下面考虑基阵处于不同接收深度情况下，对水下目标分辨的性能。水下目标深度为35 m，临界深度设定为20 m，基阵接收深度由7 m变化至75 m，不同接收深度下水下目标分辨结果如图9所示。可以看出，当接收深度逐渐增加到跃层上边界以下深度时，水下目标分辨正确率显著提高，接收深度大于20 m时，水下目标分辨正确率可达90%以上。

图9 不同接收深度时水下目标分辨结果Fig.9 The discrimination accuracy with different receiver depths

3)临界深度。

假定水面目标深度为7 m，水下目标深度为35 m，选定的临界深度由10 m变化至20 m，不同临界深度时水面目标和水下目标分辨结果如图10所示。可以看出，无论对于水面目标还是水下目标，设定的临界深度与目标深度差异性越大，分辨正确率越高，仿真条件下，临界深度大于13 m时，水面目标和水下目标判决正确率均大于90%。

图10 不同临界深度时水下目标分辨结果Fig.10 The discrimination accuracy with different critical depths

4)目标深度。

设定临界深度为15 m，水下目标深度由20 m变化至70 m，目标位于不同深度时分辨结果如图11所示。可以看出，随水下目标深度增加，激发的反转模态能量增强，分辨正确率增大，当水下目标深度大于25 m时，分辨正确率可达95%以上。

图11 不同目标深度时水下目标分辨结果Fig.11 The discrimination accuracy with different target depths

5)接收孔径。

水下目标深度为35 m，基阵接收深度为70 m，设定临界深度为20 m，基阵孔径分别为100、200、300、400、500 m时，水下目标分辨正确率如图12所示，随接收基阵孔径增大，水下目标分辨正确率提高，在仿真条件下，分辨正确率均大于90%。

图12 不同基阵孔径下水下目标分辨结果Fig.12 The discrimination accuracy with different array apertures

6)目标方位。

水下目标深度为35 m，基阵接收深度为70 m，设定临界深度为20 m，对不同方位的水下目标(正横方向为90°)分辨正确率如图13所示，可以看出，该方法对靠近端射方位目标具有较好的分辨性能，对正横方位目标并不适用，在仿真条件下，除正横方位外，对其他方位水下目标分辨正确率均不小于90%。

图13 不同目标方位下水下目标分辨结果Fig.13 The discrimination accuracy with different target bearings

4 结论

1)本文理论分析了浅海温跃层水文条件下的模态传播特性，根据传播路径对模态进行分类，利用水面目标和水下目标声场主导模态类型的差异性以及反转模态和反射模态水平波数数值分布差异性，通过水平阵波束形成空域滤波器设计，分别估计反转模态能量和传播模态总能量，实现了水面水下目标分辨。

2)当接收基阵位于温跃层内或温跃层以下深度时，均具有较好的分辨性能，且宽带处理能够提高分辨正确率，设定的临界深度与目标深度差越大，分辨性能越好。

3)该方法无需精确估计各阶模态幅值，避免了匹配处理需精确已知水文参数的限制，同时适用于水平接收基阵，应用更加灵活广泛，但该方法对正横方位附近目标并不适用，并且滤波器设计及能量估计需利用海洋环境参数信息，该方法的实际应用性能仍需进一步利用海试数据进行验证。