Na-Ti共掺LiFePO4电子结构及弹性性质的第一性原理研究
2022-03-18许正昊王发展何浩平
许正昊,王发展,何浩平
(西安建筑科技大学机电工程学院,西安 710055)
0 引 言
LiFePO4具有能量密度高、热稳定性好、成本低、环境友好等优点,是新一代锂离子电池正极材料的最佳选择之一[1-3]。但是其固有电子导电率和离子扩散率较低,阻碍了其在高倍率锂离子电池中的广泛应用[4-5]。并且在多次充放电使用后,材料表面可能会出现裂纹而影响到电化学性能。所以提高LiFePO4的导电率和离子扩散率以及深入了解该材料的弹性性质便成为了科研人员目前需解决的主要问题。
为了克服上述缺点,近些年来人们通过各种合成方法和材料改性来提高LiFePO4的电子导电率和离子扩散率[6-9]。阳离子掺杂作为一种有效的改性手段受到了广泛关注。Shi等[10]发现Cr元素在Li位掺杂后,其电导率与LiFePO4相比提高了8个数量级,电子导电性显著增强。李学良等[11]通过第一性原理计算,发现少量Nb掺杂可以使晶胞参数和体积增大,带隙变小并且总态密度峰明显增强。表明在LiFePO4中掺杂Nb有利于提高电池的性能。Lin等[12]发现V掺杂更可能进入Fe位而不是P位,并且随着V的掺杂,沿[010]方向的一维通道的扩散能垒显著降低。张冬云等[13]发现Ni掺杂在Li位比在Fe位效果更好,Mg在Li位掺杂也有利于电导率的增加。Zhang等[14]发现对LiFePO4进行Mg掺杂,Mg优先掺杂在Fe位而不是Li位,掺杂后导电性更强。Wang等[15]对Mo掺杂LiFePO4后的化合物进行分析得知掺杂后电导率增加。Hou等[16]对Sn掺杂LiFePO4进行计算后发现,Sn掺杂可以调节带隙和局部电荷转移并提高充电的电化学性能。Gu等[17]发现Na和V共掺LiFePO4可以提高容量并保持良好的循环稳定性。Luo等[18]计算了Na和Mn共掺LiFePO4的电子结构发现,共掺不仅提高了材料的电导率而且还提高了材料的局部结构稳定性。
综上所述,确定掺杂位置以及掺杂量成为了改善LiFePO4电子导电率和离子扩散率的关键。基于诸多掺杂研究发现,同族元素之间因为具有相似的原子半径与结构性质,所以经常成为掺杂元素的首选。Na和Li元素不仅属于同族元素,有着相似的原子半径,并且在Na掺杂后LiFePO4的锂离子沿一维通道扩散的阻力变小,材料的电子导电性会得到明显提高[19]。Ti和Fe元素虽不是同族,但属同周期,有着相似的核外电子排布。并且Ti的掺杂会使LiFePO4的振实密度、高倍率下循环次数得到显著提高[20]。同时,正极材料的机械性能也对其电化学性能有很大程度的影响,稳定性过差会导致材料的相变和降解,从而影响电池的充放电性能[21]。所以本文通过在Li位掺Na、Fe位掺Ti的方式,采用基于密度泛函理论的第一性原理方法来研究共掺体系的电子结构以及弹性性质,试图揭示其微观机制从而为后续的实验提供理论指导。
1 理论模型与计算方法
1.1 理论模型
LiFePO4的单胞晶格参数分别为a=1.032 97 nm,b=0.601 15 nm,c=0.470 17 nm,α=β=γ=90°[22],各元素坐标分别为:Li (0,0,0)、Fe (0.282 2,0.25,0.971 6)、P (0.095 4,0.25,0.417 9)、O1(0.094 6,0.25,0.740 3)、O2(0.453 8,0.25,0.205 6)、O3(0.161 5,0.052 1,0.286 1),建立了LiFePO4的1×1×2超胞模型,用一个Na替代超胞中的Li,再用一个Ti替代超胞中的Fe,建立了LiFePO4与Na-Ti共掺LiFePO4的模型。由于能量越低体系越稳定,所以在经过不同掺杂位点组合的计算之后,掺杂位点选取如图1(b)所示,后续的性质计算都在此模型基础上完成。
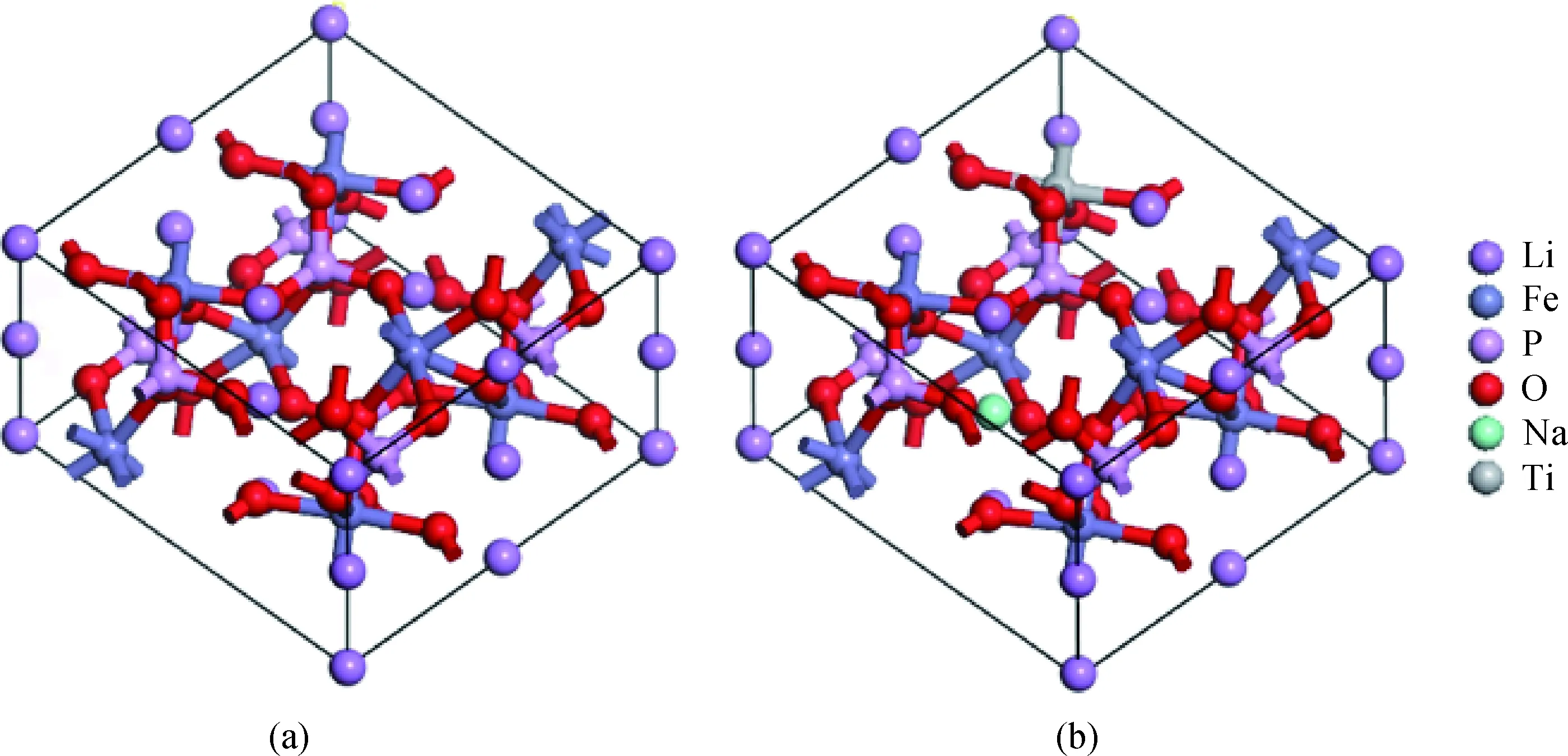
图1 未掺杂(a)以及Na-Ti共掺杂模型(b)Fig.1 Model of (a) LiFePO4 and (b) Na-Ti co-doped LiFePO4
1.2 计算方法
本文的计算基于密度泛函理论(DFT)的第一性原理方法,利用CASTEP软件完成计算,该方法可以精确地计算出固体的电子结构。建模后首先对各体系进行结构优化,计算中采用广义梯度近似(GGA)的超软赝势来描述离子与价电子之间的相互作用,采用GGA-PBE泛函计算方法来处理电子之间的交换关联能。自洽场计算时,SCF设置为1×10-6eV/atom,平面波截断能设置为580 eV,K点设置为3×4×5,选用的价电子组态为:Li:1s22s1、Na:2s22p63s1、Ti:3d24s2、Fe:3d64s2、O:2s22p4、P:3s23p3。
2 结果与讨论
2.1 晶体结构分析
结构优化是为了得到稳定的结构后进行后续的性质分析。经过结构优化之后,表1是LiFePO4和Na-Ti共掺后各体系的晶胞参数。由于Na原子半径(0.191 nm)比Li(0.154 nm)原子大,并且Ti原子半径(0.145 nm)比Fe原子半径(0.127 nm)也要大,所以掺杂后体系的晶胞参数比本征体系略微增加。在结构优化完成之后计算了掺杂体系的形成能,即反应初始态与终态的能量差。形成能的计算公式为:
Eform=Etot(NT-LFP)-Etot(LFP)-μ(NT)+μ(LF)
(1)
式中:Etot(LFP)和Etot(NT-LFP)分别为掺杂前后体系的总能量;μ(NT)为掺杂原子的化学势,其值为单个自由Na原子和Ti原子的总能量。μ(LF)为被取代原子的化学势,其值为单个自由Li原子和Fe原子的总能量。计算所得该掺杂体系的形成能为-0.28 eV,形成能越小则说明掺杂反应越容易进行,当形成能为负值时说明反应可以自发进行。

表1 优化前后的晶胞参数Table 1 Cell parameters before and after optimization
2.2 能带分析
LiFePO4和共掺体系的能带结构如图2和图3所示,由于原子内部电子的占据轨道数不同,所以各个轨道之间形成了不同的能级结构,根据能级的高低与填充情况将能带定义为三部分,分别是占据高能区的导带、低能区的价带以及两者之间的间隙。当导带底与价带顶处于同一高对称点时,称这种带隙为直接带隙;反之则称为间接带隙。相较于间接带隙,直接带隙的电子跃迁要更容易一些,并且带隙越窄,导电性越好。同时由于计算模块所使用的广义梯度近似存在一定的局限性,未妥善处理电子间的交换关联相互作用,导致计算值整体偏小于实验值。但各个体系的计算参数设置保持一致所以并不影响本文对LiFePO4及其掺杂体系变化规律的分析。计算结果显示体系经过掺杂后带隙值由0.695 eV降低至0.473 eV,并且掺杂后的能带结构整体下移,使得载流子浓度变大,材料导电性增强。

图2 LiFePO4的能带结构Fig.2 Band structure of LiFePO4
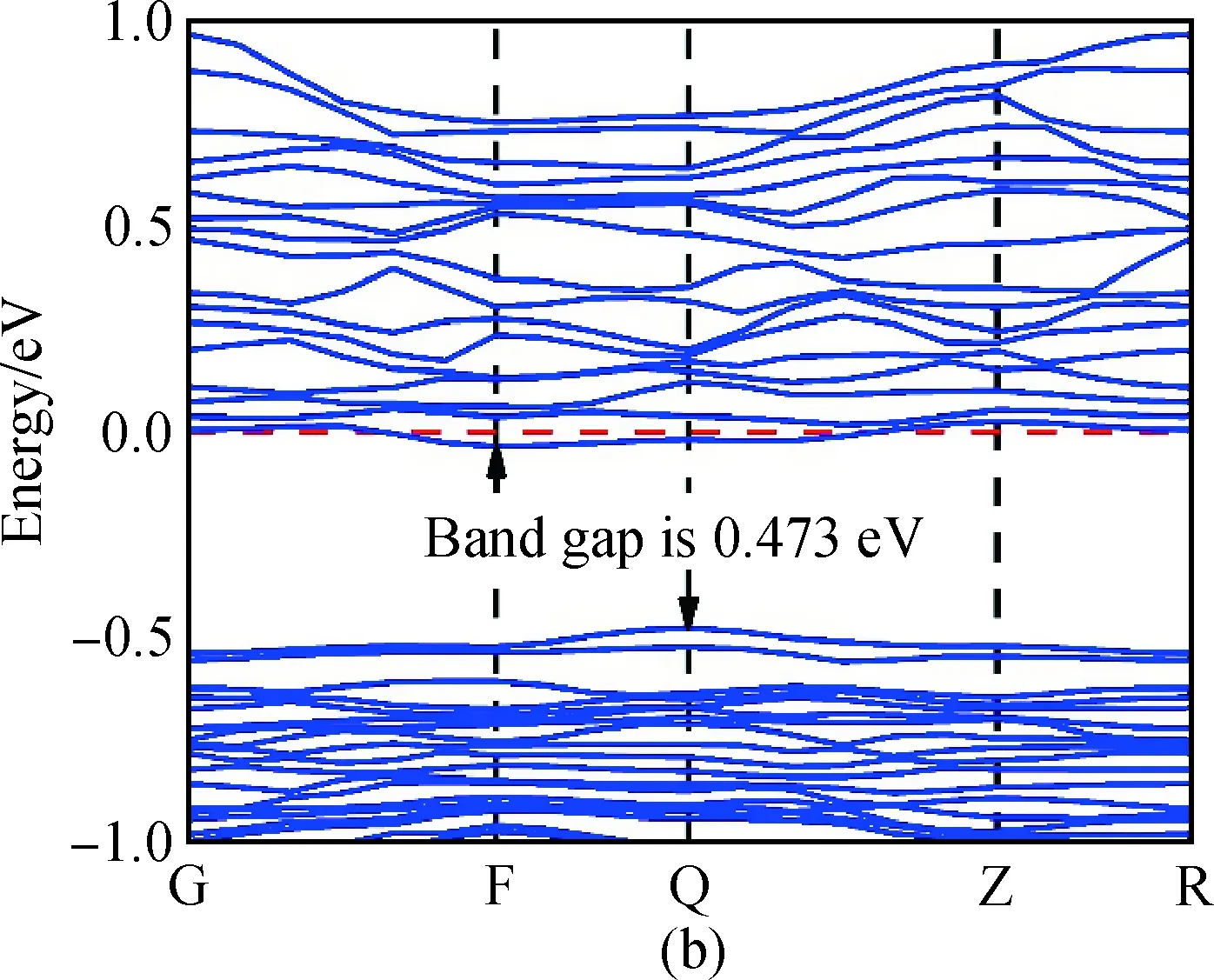
图3 Na-Ti共掺杂LiFePO4的能带结构Fig.3 Band structure of Na-Ti co-doped LiFePO4
2.3 态密度分析
纯LiFePO4的态密度如图4所示,其价带分为三部分,分别为-45 eV下价带附近、-25~-20 eV中价带附近以及-10~0 eV上价带附近。在下价带附近主要由Li的s态贡献,由于距离费米能级较远,与周围的原子只有微弱的共价作用,所以该区域对结果的影响可以忽略。在中价带附近主要由P和O的2p态贡献,而在上价带主要由O的2p态和Fe的3d态贡献。同时少量的O的2p态和Fe的3d态在导带底部进行杂化,因此LiFePO4具有一定的共价性。当Na-Ti共掺LiFePO4时,态密度如图5所示,总态密度图的价带部分出现了许多新的峰值:-60 eV附近的主要由Ti的s态贡献,在-50~-45 eV附近的主要由Li的s态贡献,在-35 eV附近的主要由Ti的p态贡献。
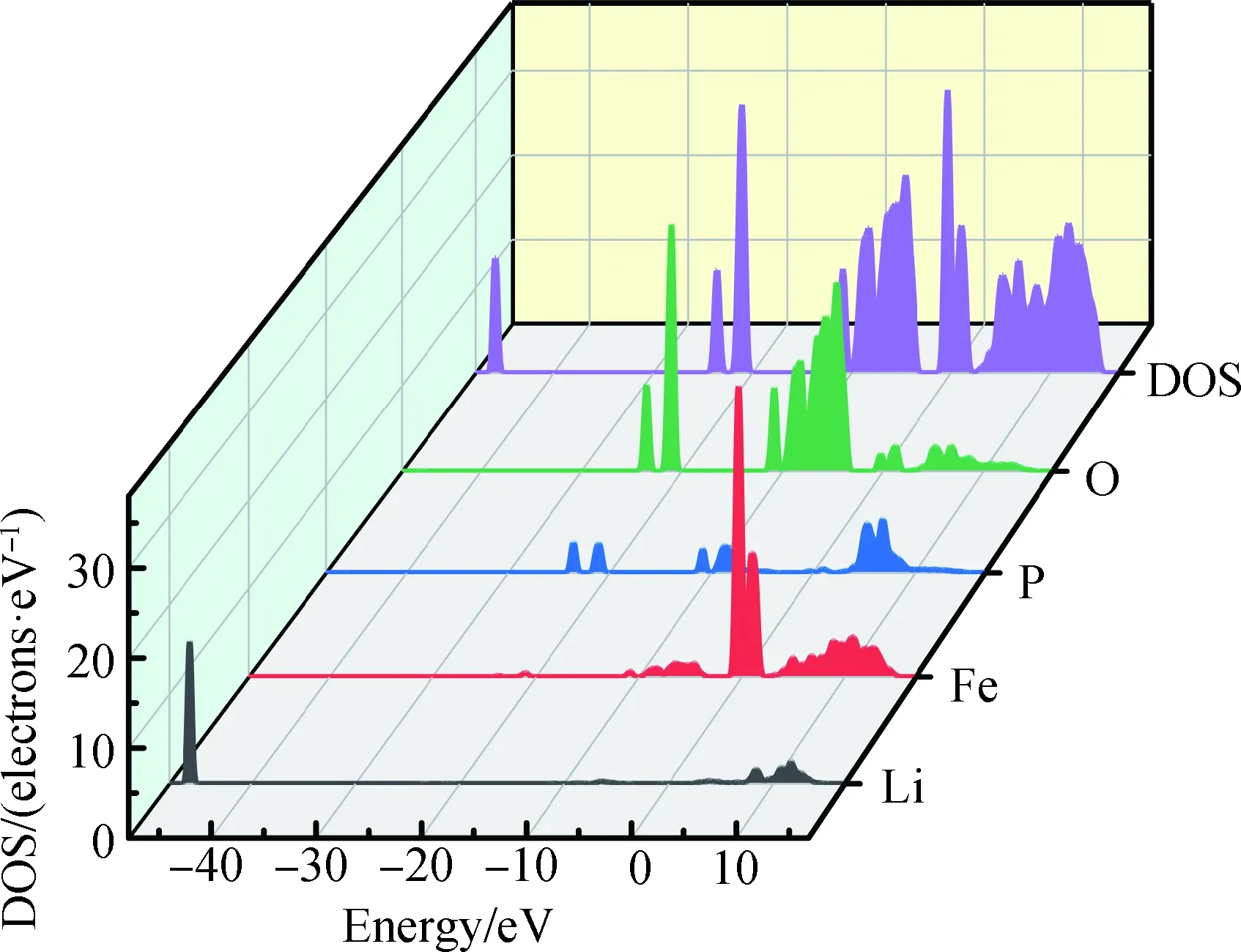
图4 LiFePO4的态度图Fig.4 State density figure of LiFePO4
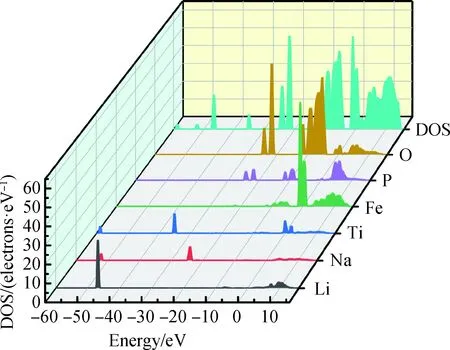
图5 Na-Ti共掺杂LiFePO4的态密度图Fig.5 State density figure of Na-Ti co-doped LiFePO4
2.4 布居分析
原子的电荷布居值体现了原子的得失情况,键的布居值展现了键的共价性与离子性。本文对掺杂前后的体系分别进行原子电荷布居以及键布居分析,如表2所示,表中数据均取平均值。在本征LiFePO4体系中,Li、Fe和P原子带正电荷主要失去电子,电荷布居数分别为+1.05、+0.73和+2.11,O原子带负电主要获得电子,其电荷布居数为-0.97。进行掺杂后发现Na和Ti的电荷布居数分别为+0.98和+1.11,而且Fe原子的电荷布居数减小到+0.64,失电子能力变弱。计算表明掺杂后的Ti—O键比Fe—O键的布居值高,说明Ti—O键比Fe—O键的共价性更强。

表2 电荷布居和键布居分析Table 2 Atomic charge population and bond population analysis
2.5 锂离子迁移势垒分析
在电池正极材料中锂离子迁移势垒对电池性能有着重要的影响,为了研究锂离子在本征LiFePO4中沿[010]方向上扩散的能垒,采用过渡态搜索方法得到在未掺杂前锂离子在[010]方向上迁移的势垒为0.34 eV,掺杂后势垒降低为0.25 eV,如图6所示。说明锂离子在迁移过程中需要消耗的能量减少,使得迁移更加容易发生,同时也提高了材料的导电性。
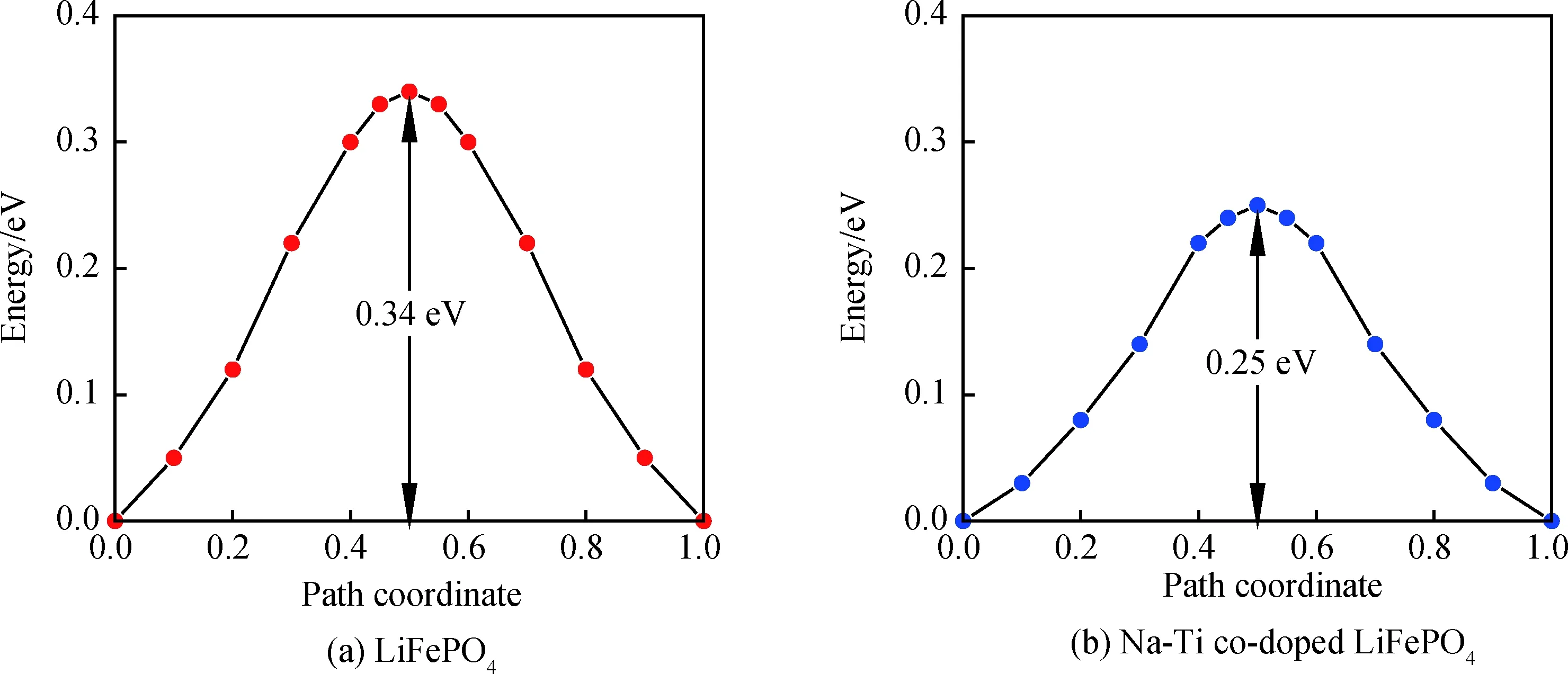
图6 锂离子的扩散势垒图Fig.6 Diffusion barrier diagram of lithium ion
2.6 弹性性质分析
在描述物质机械性质方面,弹性常数发挥着重要的作用。而利用密度泛函理论可以得到可靠的弹性常数数值[23-24]。本文通过计算得到了LiFePO4以及Na-Ti共掺LiFePO4的弹性常数,从而得到材料的体积模量、剪切模量、杨氏模量、泊松比。其机械稳定性可定义为[25]:
C11>0,C22>0,C33>0,C44>0,C55>0,C66>0
[C11+C22+C33+2(C12+C13+C23)]>0
(C11+C22-2C12)>0,(C11+C33-2C13)>0
(C22+C33-2C23)>0
(2)
式中:C11、C22、C33、C44、C55、C66、C12、C13、C23分别为正交晶系的9个独立弹性常数。由表3可知,计算的弹性常数与文献值[26]一致并且纯LiFePO4及其掺杂体系均满足机械稳定性条件,表明杂体系都可以稳定存在。
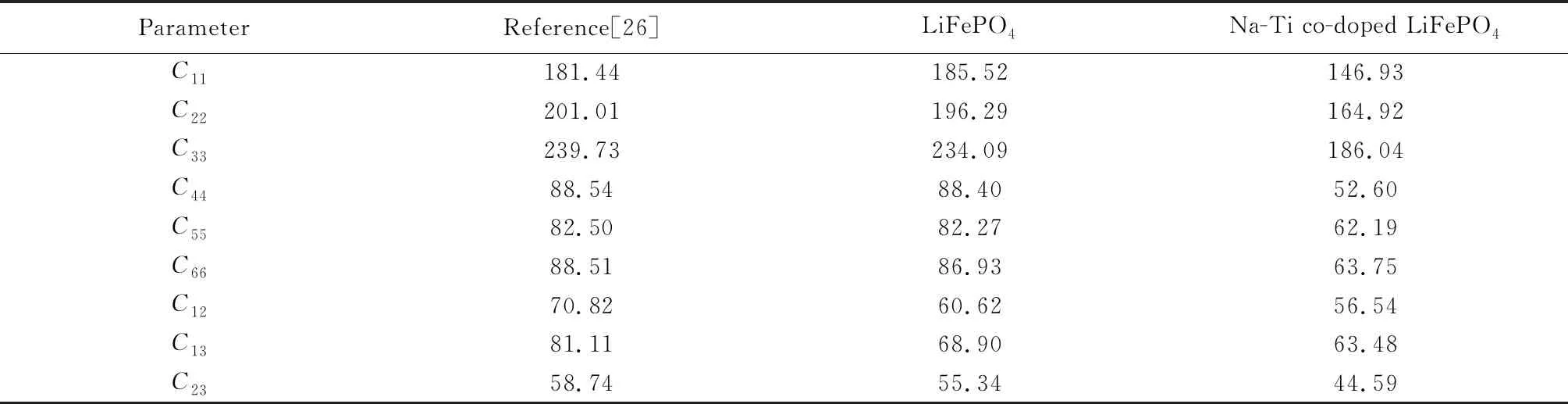
表3 LiFePO4及其掺杂体系的弹性常数Table 3 Elastic constants of LiFePO4 and its doping system
根据已经得到的弹性常数,可以通过VRH近似方法得到其体积模量B、剪切模量G、杨氏模量E以及泊松比γ,其中基于Voigt和Reuss方法得到的数值分别代表弹性模量的上下限[27],计算公式为:
BV=(1/9)[C11+C22+C33+2(C12+C13+C23)]
(3)
GV=(1/15)[C11+C22+C33+3(C44+C55+C66)-(C12+C13+C23)]
(4)
BR=Δ[C11(C22+C33-2C23)+C22(C33-2C13)-2C33C12+C12(2C23-C12)+
(2C12-C13)+C23(2C13-C23)]-1
(5)
GR=15{4[C11(C22+C33+C23)+C22(C33+C13)+C33C12-C12(C23+C12)-C13(C12+C13)-
C23(C13+C23)]/Δ+3[(1/C44)+(1/C55)+(1/C66)]}-1
(6)
Δ=C11(C12C23-C13C22)+C23(C12C13-C23C11)+C33(C11C22-C12C12)
(7)
式中:BV与GV分别是通过Voigt方法得到的体积模量上限;BR与GR分别是通过Reuss方法得到的体积模量下限。基于Hill方法得到的平均体积模量B和平均剪切模量G可定义为:
BH=1/2(BV+BR)
(8)
GH=1/2(GV+GR)
(9)
杨氏模量E和泊松比γ的计算公式定义为[28]:
E=9BHGH/(3BH+GH)
(10)
γ=(3BH-2GH)/2[(3BH+GH)]
(11)
式中:E与γ分别代表杨氏模量与泊松比。根据以上公式得到的结果以及文献值如表4所示。
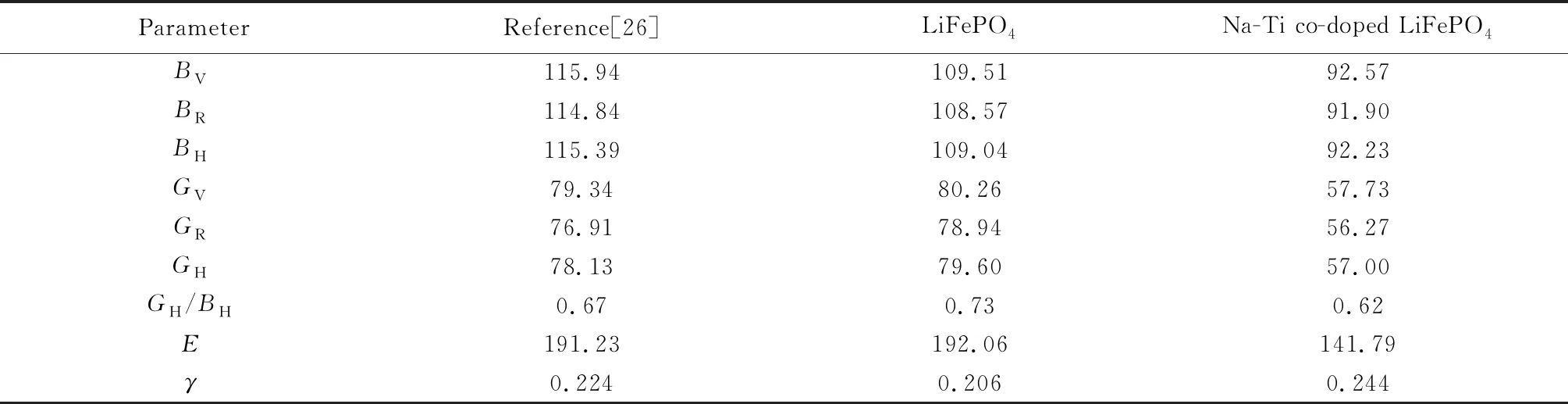
表4 LiFePO4及其掺杂体系的弹性常数Table 4 Elastic constants of LiFePO4 and its doping system
体积模量B是反映材料抵抗外界压力所引起体积变化的物理量,剪切模量G是反映材料抵抗剪切应变能力的物理量,杨氏模量E是反映固体材料抵抗形变能力的物理量,由表可知,掺杂后体系的B、G、E都有明显减小,表明在掺杂后,材料的硬度和强度都有所下降,形变能力有所提高。泊松比γ可用来判断材料的延展性和脆性[29]。当泊松比γ<0.33时,表明该材料为脆性材料;当泊松比γ≥0.33时,表明该材料为塑性材料。由表可知,纯LiFePO4及其掺杂体系都为脆性材料,且由泊松比越小脆性越大可知,掺杂后的体系脆性减弱。根据Pugh标准,平均剪切模量和平均体积模量的比值GH/BH也可以用来衡量材料的延展性:当GH/BH≥0.5时表明为脆性材料;当GH/BH<0.5时表明为塑性材料[30]。由表可知,纯LiFePO4及其掺杂体系的平均剪切模量和平均体积模量的比值GH/BH均大于0.5,且掺杂后的比值小于未掺杂的体系,表明掺杂后的材料塑性强于未掺杂的材料。
本质上,现在已知的所有晶体都是弹性各向异性的,并且对于该性质的描述也有许多方法,在本研究中,引入通用各向异性系数AU[31],分别对应体积模量和剪切模量的各向异性百分比AB、AG以及剪切各向异性系数A1、A2、A3[32],来描述纯LiFePO4以及Na、Ti共掺后体系的弹性各向异性,上述各弹性各向异性系数都可以通过弹性常数得到,计算公式定义为:
(12)
(13)
(14)
式中:AU为通用各向异性系数;AB为体积模量的各向异性百分比;AG为剪切模量的各向异性百分比。处于(011)和(010)方向的(100)切面的剪切各向异性系数A1可以定义为:
(15)
处于(101)和(001)方向的(010)切面的剪切各向异性系数A2可以定义为:
(16)
处于(110)和(010)方向的(001)切面的剪切各向异性系数A3可以定义为:
(17)

表5 LiFePO4及其掺杂体系的各向异性系数Table 5 Anisotropy coefficient of LiFePO4 and its doping system
可以看出,对于各向同性的晶体,A1、A2、A3的值相同。当A1、A2、A3不同时,表明该晶体各向异性,由表可知LiFePO4在(100)、(010)、(001)三个切面的各向异性系数分别为1.254 8、1.029 3、1.334 5,表明LiFePO4在这三个切面上各向异性,且在(001)切面的各向异性最强,在Na、Ti共掺后,A1、A2、A3同时减小,但变化规律与LiFePO4相同,即A2 采用基于密度泛函理论的第一性原理计算方法,对Na、Ti共掺LiFePO4体系的电子性质计算结果显示晶胞参数增大,同时带隙值由0.695 eV降低至0.473 eV,锂离子迁移势垒由0.34 eV降低至0.25 eV,减小了电子跃迁时所需的能量,有利于增强材料的导电性;对纯LiFePO4以及Na、Ti共掺LiFePO4体系的弹性性质计算结果显示,掺杂后的体积模量、剪切模量以及杨氏模量均有不同程度下降;由计算的泊松比显示掺杂前后均为脆性材料,但Na、Ti共掺杂后的材料塑性强于纯LiFePO4;对纯LiFePO4以及Na、Ti共掺LiFePO4体系的各向异性计算结果显示,Na、Ti共掺后晶体的各向异性减弱,提高了LiFePO4的延展性。3 结 论
