基于贝叶斯参数优化的无模型自适应硅单晶直径控制
2022-03-18林光伟张西亚高俊伟高德东
林光伟,王 珊,张西亚,彭 鑫,高俊伟,高德东
(1.青海大学机械工程学院,西宁 810016; 2.阳光能源(青海)有限公司,西宁 810000)
0 引 言
直拉法硅单晶的制备直接推动了电子信息产业与光伏发电产业的飞速发展,但高新技术的突飞猛进对硅单晶提出了更高的品质要求,包括更大的晶体尺寸以及更均匀的直径[1-2]。由于生产条件的限制,目前所生产的大尺寸硅单晶的有效直径受到极大影响,因此解决这一问题是非常重要的。考虑到直拉硅单晶的生长过程涉及多场多相耦合与复杂的物理化学变化,有研究者发现在晶体生长过程中工艺参数不稳定容易引起硅单晶直径波动,导致最终晶体的有效直径减小。为此,研究人员进一步对影响硅单晶直径波动的因素进行分析。Brown等[3]研究发现,坩埚上升速度以及籽晶棒的拉速不匹配会影响硅晶体的结晶速率,导致直径不稳定。Gevelber等[4-5]提出,晶转与埚转速度差异较大,熔体涡流中心会与籽晶轴轴心偏离,导致硅晶体生长发生偏移,使硅晶体产生内部缺陷从而影响晶体直径。Galazka等[6]通过分析直拉法制备硅单晶的热传导过程,发现不均衡的热场温度分布也会影响结晶速率,导致晶体的直径大小受到一定的影响。国内学者刘丁等[7-8]总结提出,直径均匀性与硅晶体内部的缺陷位错有重要关系,直径变化越大,晶体内部产生缺陷和位错的可能性越大,导致硅晶体的品质下降,因此相对于追求更大尺寸的晶体,如何制备出均匀的直径晶体更为重要。
直拉法制备硅单晶是在高温高压的环境中,持续通氩气将高纯度的多晶硅原料熔化,在单晶炉中完成引晶、放肩、等径及收尾等过程[9],最终形成硅晶体。但在具有多时变、大时滞、非线性及多场相互耦合的生长环境下,存在信息获取难、测量难等问题,要制备出均匀的晶体直径,就需要研究硅晶体生长过程中关键工艺参数的控制问题。因此,研究者分别从生长机理和PID控制原理出发,建立了晶体生长过程的控制基础。生长机理控制是在对整个生长过程都研究分析透彻的基础上建立的,因此Abdollahi等[10-12]就从基础的晶体生长机理过程进行研究,建立了晶体生长过程中提拉速度影响晶体直径变化的动力学几何模型,并基于该模型设计了以提拉速度为输入、晶体直径为输出的控制器,最后实现了通过调节提拉速度来控制晶体直径的目的。而Winkler等[13-16]在分析前人提出的基于模型的多回路系统控制晶体直径上,发现该系统用于控制时参数未知量太多,控制模型所达到的精度不够,因此提出一种试图克服这些局限性的控制系统,即通过忽略晶体生长过程中热动力学过程的影响,仅主要考虑流体力学产生的重要作用,建立几何模型,设计了针对晶体直径和生长速度的双闭环控制结构,通过控制工艺参数最终实现对晶体直径的有效控制。但以上两个具有重要影响力的学者所提出的控制过程及方法都涉及庞大的数学演算和推理,同时求解其中的数值解需要耗费大量的时间。而PID直径控制是目前广泛应用的控制手段,主要是通过控制加热功率与提拉速度两个工艺参数来实时调节晶体直径。如图1所示,当PID控制系统监测到设定直径值与实际测量的晶体直径值存在偏差时,会通过调节提拉速度控制晶体直径,但在这个过程中响应速度会影响控制的精准性,因此利用温度控制系统去对比实际温度,适当弥补温度之间的偏差进而与提拉速度共同控制晶体直径[17-18]。但在实际的PID控制晶体生长过程中,监测的不准确以及反馈存在时滞是导致直径控制效果降低的重要原因,因此学者们为提高最终的晶体品质,对PID直径控制也进行研究分析。在使用CCD相机进行直径检测时存在较大的检测误差[19-20],乔朝晖[21]将无味卡尔曼滤波技术应用于直拉法晶体生产过程中弯月面的高度估计,进而计算出晶体的直径,并将此计算值用于替代CCD相机所反馈的晶体直径,提高了控制精度。而张晶等[22]在利用热场温度进行PID控制的基础上,设计广义预测控制器重新对晶体的直径进行控制,该控制器对直径的检测不准确方面有很好的改善。姜舰等[23]通过实验分析不同PID控制参数对晶体生长的影响,并选取最优的PID控制参数进行实验得到了更大更均匀的晶体直径。以上学者对PID的直径控制研究工作已经取得较大进展,但依然存在当硅单晶生长过程发生微小变动时,PID参数需要重新整定以及对生长过程复杂及参数众多的硅单晶生长系统控制响应延迟的问题,因此,目前广泛应用于直拉法制备硅单晶中的PID控制系统对直径波动问题依旧没有很好解决。
综上,为实现均匀的晶体直径所研究的直径控制方法有基于机理模型的控制,也有在机理模型不准确、不确定性大时采用的PID直径控制。然而硅单晶生长过程是一个集总参数的大系统,任何微小参数的波动都会影响晶体生长,导致最终的晶体直径仍发生较大的波动。因此,针对生长机理控制以及PID直径控制存在的缺陷,本文采用基于数据驱动的无模型自适应(model-free adaptive control, MFAC)方法进行直径控制,通过分析晶体生长过程中复杂的生长环境及多参数共同作用的情况,将晶体生长过程中的工艺参数,即加热器功率与坩埚上升速度作为输入,晶体直径数据作为输出建立非线性系统,并在此基础上实现晶体直径的控制。虽然MFAC直径控制能解决晶体生长模型未知以及大时变、大时滞的问题,但在控制模型的建立过程中引入的超参数也会影响直径的控制过程,因此为实现硅单晶生长过程中直径的准确控制,本文提出基于贝叶斯参数优化的MFAC直径控制模型,并通过MATLAB仿真实验结果证明了控制模型的有效性和优越性。

图1 PID控制晶体生长系统演示Fig.1 Demonstration of PID control crystal growth system
1 硅单晶直径控制模型建立
要实现对硅单晶直径的控制,需要先明确控制的工艺参数。在硅单晶生长过程中,影响晶体直径的工艺参数较多,在PID控制时常采用提拉速度与加热器的功率作为控制参数,这是因为这两个参数易于监测,如图1所示,加热器的功率输出可以通过电压电流控制,提拉速度可以通过伺服电机控制。但通过分析发现,提拉速度的监测装置安装在与籽晶轴连接的伺服电机上,在硅单晶生长过程中籽晶轴会受到氩气吹拂从而影响监测数据,同时当籽晶轴提拉的晶体处于硅熔体中时,晶体旋转中心与硅熔体的旋转中心处于不同轴心时也会导致所监测的提拉速度发生偏差。因此,结合上述原因,考虑同样易于监测与控制的坩埚上升速度来代替提拉速度。这是由于坩埚中的硅熔体在生长过程中会不断转化为固态而被籽晶提起,液面在坩埚中的位置也会不断下降,所以当给予合适的埚升速度来保持液面在热场中的相对位置不变时,能稳定固液界面处的温度梯度,进一步实现硅单晶生长的平稳进行,避免硅单晶直径出现大的波动,同时控制坩埚上升速度的伺服电机安装在坩埚埚帮的底部,在伺服电机的工作中受到的影响相对提拉位置更小。因此在本文中为提高控制参数的准确性,选择坩埚上升速度与加热器功率作为控制参数,建立硅单晶直径控制模型。
1.1 控制算法
硅单晶的生长是个复杂的非线性离散系统,通过机理控制以及PID控制都存在难题,因此,避开对硅晶体生长过程分析,考虑选取坩埚上升速度与加热器的功率数据作为控制的输入,硅单晶直径作为输出。根据侯忠生教授等[24-26]所提出的MFAC控制,引入伪雅克比矩阵(pseudo Jacobian matrix, PJM)将上述明确的以坩埚上升速度与加热器的功率作为输入、硅单晶直径作为输出的非线性离散系统等价转化为虚拟的、动态的线性数值模型,进一步实现对硅晶体生长未知系统的MFAC控制。
首先,对双输入、多输出非线性离散系统进行分析。
(1)
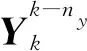
假设1:f(·)关于当前控制输入信号u(k)的偏导数是连续的。

Δy(k+1)=ΦTΔU(k)
(2)

u(k)=u(k-1)+[y*(k+1)-y(k)]·ρΦ(k)/(λ+Φ2(k))
(3)
(4)

(5)
式中:ε为无穷小的数,表示该重置算法的引入能进一步保证在时变系统中依然保持很强的控制能力;u(k)为k时刻硅单晶生长中坩埚上升速度与加热器的功率的输入;y(k)为k时刻晶体直径的输出,通过设定初始时刻的工艺参数及晶体直径数值可实现对晶体直径的控制。
1.2 稳定性分析
对于硅单晶直径控制模型,在满足y(k+1)关于y(k)和坩埚上升速度与加热器功率u(k)的偏导数连续且满足广义Lipschitz的条件下,当y*(k+1)和y(k+1)相等且为一个定值常量时,控制算法式(5)达到稳定,此时存在a>0保证系统的跟踪误差收敛且输入输出均有界,稳定性分析证明如下。


(6)
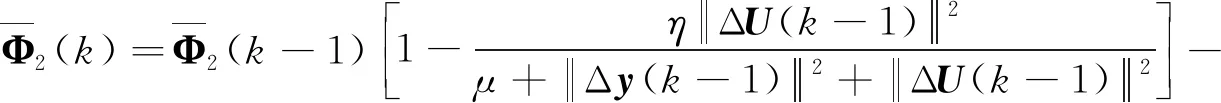
(7)


存在步长因子η∈(0,1],μ>0,此时有


由e(k)=y*(k)-y(k)为控制输出的误差值,则
(8)

1.3 动态控制过程
式(5)建立了硅单晶直径的控制算法,同时证明了该算法的稳定性,但在硅单晶生长中,对于控制的输入输出数据都要实时产生的,因此为了模拟实时控制的条件,在上述MFAC控制算法的基础上需引入实时的硅单晶生长中直径变化值。
考虑到直接采用实际拉晶过程中的直径数据时,数据量过于庞大同时很难导入控制算法中,因此本文根据CL120-97炉的已有数据,建立了以埚升速度与加热器功率作为输入,晶体直径作为输出的拟合函数,该函数能为控制过程提供连续的直径变化数据,并且将该拟合函数嵌入MFAC算法中更容易实现。本文中选取了1 200组实时生产数据,在表1中只显示部分数据。由于拟合的精确度对控制过程没有影响,对于2个自变量与1个因变量的拟合函数中常采用的是二次非线性拟合,因此,得到拟合函数表达式为:

(9)
式中:u1代表坩埚的上升速度;u2代表加热器的输出功率;y代表晶体直径。通过该表达式,模拟出了在实际晶体生长中会出现的直径变化情况。同时在结合式(3)的基础上,将式(9)中模拟出的直径值作为y(k)的变化值,进一步实现对实时硅单晶直径的控制。

表1 晶体生长数据Table 1 Crystal growth data
因此,在式(5)MFAC控制算法的基础上,令u=[u1u2],Φ=[φ1φ2]T,得到双输入、单输出MFAC动态控制算法为:
(10)
在硅单晶直径控制过程中,用简化的示意图表示算法过程,如图2所示。在给定初始k=1时刻的伪偏导数Φ(1),控制输入u1(1)u2(1)及k=1,2时刻硅单晶直径y(1)y(2)的前提下,可以计算出k=3时刻的硅单晶直径y(3),此时对比设定的晶体直径与控制输出直径的差值,即y*-y(3)的大小,来调节k=2时刻的伪偏导数Φ(2)与控制输入u1(2)u2(2),进一步计算下一时刻k=4时刻的硅单晶直径y(4),上述过程不断迭代计算,最终计算到k时刻,y*-y(k)的值接近0或等于0时,晶体直径达到设定值,此时控制算法稳定运行,实现了对晶体直径的有效控制。

图2 直径控制算法动态演示Fig.2 Dynamic demonstration of diameter control algorithm
2 基于贝叶斯的超参数优化
2.1 超参数的影响
在硅单晶直径控制模型中存在的超参数ρ、η、μ、λ需要进行初始设定,这些超参数对于控制模型的性能都有影响,并且不同的初始设定参数会带来不同的计算量与时间成本,但满足控制要求的合理设定范围却很难获得。
在MFAC参数整定的研究[29-30]中发现四个超参数的敏感程度依次为λ>η>μ>ρ,因此为了降低超参数调整的复杂度,选取敏感程度较高的λ,η两个超参数进行MATLAB仿真实验,以验证本文中超参数对硅单晶直径控制的影响。
在进行仿真实验前,设定目标晶体直径为230 mm,并根据实际数据设定以下初始值:
y(1)=224.7,y(2)=223.1,u1(1)=0.161 0,Δu1(1)=-0.012,u2(1)=45.19,Δu2(1)=-0.05
而对于超参数的初始设定是根据参数整定研究中所得到的有效值并进行随机组合,并且λ∈(0,2],η∈(0,1],因此初始设定值为:
λ=0.5,η=0.5,μ=0.5,ρ=0.4,φ1=0,φ2=0.15;λ=1.0,η=0.2,μ=0.5,ρ=0.4,φ1=0,φ2=0.15;λ=1.1,η=0.8,μ=0.5,ρ=0.4,φ1=0,φ2=0.15;λ=1.3,η=0.2,μ=0.5,ρ=0.4,φ1=0,φ2=0.15;λ=1.5,η=0.3,μ=0.5,ρ=0.4,φ1=0,φ2=0.15
通过仿真实验,得到实验结果如图3~5所示。图3是在不同的超参数组合下,硅晶体直径的控制结果,可以看出晶体直径最终都达到均匀稳定的状态,但超参数对整个控制过程有重要影响。同时从图3中可发现,超参数不同的取值会影响直径达到稳定的迭代次数,也会影响控制过程中的波动情况,也就是说用于实际晶体生长控制时,晶体达到稳定直径的耗时较长,并且在晶体生长的初始阶段,晶体的直径变动范围较大。
图4是 MFAC控制模型对埚升速度与加热器功率的控制结果。可以看出在160次迭代后,对于硅单晶生长过程中输入的控制均达到了稳定状态。但此时由于超参数的取值不同,最大的加热器功率输入达到了57.347 1 kW,最小的加热器功率输入为39.847 5 kW,两者相差较大,表明超参数对生长过程中的输入功率也有较大影响,用于实际生产时一定会影响成本的波动。同时从图4中可以发现,最大的坩埚上升速度输入在合理的范围,但最小的坩埚上升速度输入小于0,表明此时的控制效果很差,维持最小的坩埚上升速度输入时对整个晶体生长过程都有负面影响。

图3 控制晶体直径的仿真结果Fig.3 Simulation results of controlling crystal diameter
图5是直径误差结果,可以看出存在最大误差与最小误差的比值达到40倍的情况,也存在500次迭代过程中还没收敛的情况。表明采用硅单晶直径控制的效果与超参数的取值有密切关系,如何调整超参数会直接影响到硅单晶生长过程中的直径波动范围,以致影响最终的硅晶体品质。

图4 控制输入的仿真结果Fig.4 Simulation results of controlling input

图5 控制晶体直径的误差结果Fig.5 Error results of controlling crystal diameter
从图3~5中可以得出,MFAC硅单晶直径控制模型达到了控制晶体直径的作用,在数次迭代后都维持了稳定的控制,但也同样得出超参数对控制的重要影响。总结以上结果,如表2所示。

表2 仿真结果数据Table 2 Simulation result data
从表2中可以得出,硅单晶直径控制模型能够实现对于晶体直径的均匀控制,同时稳定硅晶体生长过程,但在实际的晶体生长过程中,坩埚的上升速度是0.1~0.3 cm/min,加热器功率是44~48 kW,表明由于超参数的存在,控制输入的数据已经超出合理的工艺参数范围,必定会影响整个硅晶体生长过程。另外,直径控制模型中超参数的取值不同,仿真过程的迭代次数太多,耗费的时间也会增加,导致在晶体生长的初始阶段,晶体的直径也会产生较大的波动从而影响最终的晶体品质。因此,在对MFAC硅单晶直径控制模型进行仿真实现后得出,控制模型中涉及的超参数λ、η对整个硅单晶生长过程有重要影响。
2.2 贝叶斯参数优化
硅单晶直径控制模型中的超参数是影响最终控制效果的重要因素,优化超参数λ,η来降低迭代次数并将输入参数控制在一定范围内,是实现硅单晶品质的提升过程中需要解决的问题。
在超参数优化的研究中,基础的方法是手动调参、网格搜索及随机搜索调参,其原理都是穷举法,而在深度学习迅速发展后,许多研究者开始采用模拟退火算法、遗传算法及粒子群优化算法等进化算法进行调优,另外还有基于梯度的参数优化算法等[31-32]。在本文中,采用以上优化方法迭代次数多、效率低,同时需要大规模的数据集,花费的代价太大。因此,选用迭代过程简单、目标函数少、效率更高的贝叶斯优化对以上超参数进行调优。
贝叶斯优化的核心是先验函数(prior function, PF)与采集函数(acquisition function, AC)。PF主要采用高斯过程回归,利用高斯过程增加后验概率的准确,而AC的函数中采用目前最为广泛的EI(expected improvement, EI),目的是探索方差最大的位置寻找最优[33]。
首先将上述5次仿真实验的数据样本拟合成高斯回归模型,如式(11)所示:
f(x)=gp(0,k)
(11)
式中:k=(x,x′)为协方差函数,而x=[λη]是本文需要优化的λ,η两个超参数。因此手动设置5次仿真实验样本值{(x1,y1),(x2,y2),…,(x5,y5)},得到的协方差矩阵为式(12):
(12)

Pm+1~N(μ,σ2)
μ=kTK-1fm(x)
σ2=k(xm+1,xm+1)-kTK-1k
(13)
根据上述高斯过程得到的后验概率,再进一步通过采集函数EI决定下一个采样点xm+1的选取。而EI函数依然采用explore和exploit两种策略[34],并求取未知点与f(x)差值的期望来评估是否进行选取该点。其准则函数表示为式(14):
(14)
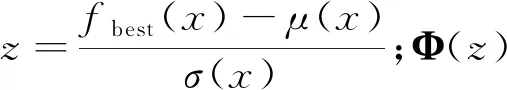
为更加直观观测整个优化过程,本文中采用三维视角,将需要优化的超参数λ、η设置为三维坐标系中的x轴与y轴,而目标位置与设定直径差值f(x)-230设置为z轴。如图7所示,每个已知点符合高斯过程的正态分布,进而通过计算方差与均值不断接近理想的位置,最后寻找到最优的超参数范围。
由于MFAC硅单晶直径控制模型中需要优化的超参数λ∈(0,2],η∈(0,1],因此该优化过程是连续的超参数寻优,可假定为二维平面内进行随机的λ、η选取。然而在本文已经手动输入一部分已知参数点的情况下,可以直接利用已知点的集合,并根据EI准则进行下一个点采样。因此通过MTALAB软件对上述贝叶斯优化过程进行仿真,最终得到的优化结果是λ∈[0.94,1.05],η∈(0,0.18]。

图6 算法流程框图Fig.6 Algorithm flow diagram

图7 贝叶斯参数优化过程演示Fig.7 Demonstration of Bayesian parameter optimization process
3 硅单晶直径控制的仿真实验
在通过首次仿真实验后发现,对超参数的优化是必要的,因此将贝叶斯参数优化得到的结果进行最终的硅单晶直径控制的仿真实验。
在进行仿真实验前,设定目标晶体直径为230 mm,并同样根据实际数据设定以下初始值:y(1)=224.7,y(2)=223.1,u1(1)=0.161 0,Δu1(1)=-0.012,u2(1)=45.19,Δu2(1)=-0.05。
根据超参数优化的合理取值范围,选取λ,η优化区间的最小值设定初始值,其他参数固定不变:λ=0.94,η=0,μ=0.5,ρ=0.4,φ1=0,φ2=0.15。
通过MATLAB软件仿真得到优化后实验结果对比如图8、图9所示。

图8 贝叶斯参数优化后的直径控制结果对比Fig.8 Comparison of diameter control results after Bayesian parameter optimization
通过贝叶斯超参数优化后的取值范围,选取优化区间的最小值,得到直径控制结果对比如图8。可以发现在迭代4次后直径就达到了设定的理想直径,相对于没有采用超参数优化前的迭代次数减少了250次以上,同时所耗费的时间成本也为优化前的1/100左右,达到了不错的优化效果。
为了验证贝叶斯优化后超参数取值范围的有效性,进一步选取优化区间的最大值进行软件仿真。同样重新进行仿真实验参数的初始化:y(1)=224.7,y(2)=223.1,u1(1)=0.161 0,Δu1(1)=-0.012,u2(1)=45.19,Δu2(1)=-0.05;λ=1.05,η=0.18,μ=0.5,ρ=0.4,φ1=0,φ2=0.15。
设定目标晶体直径为230 mm,软件仿真得到优化前后实验结果对比如图9。
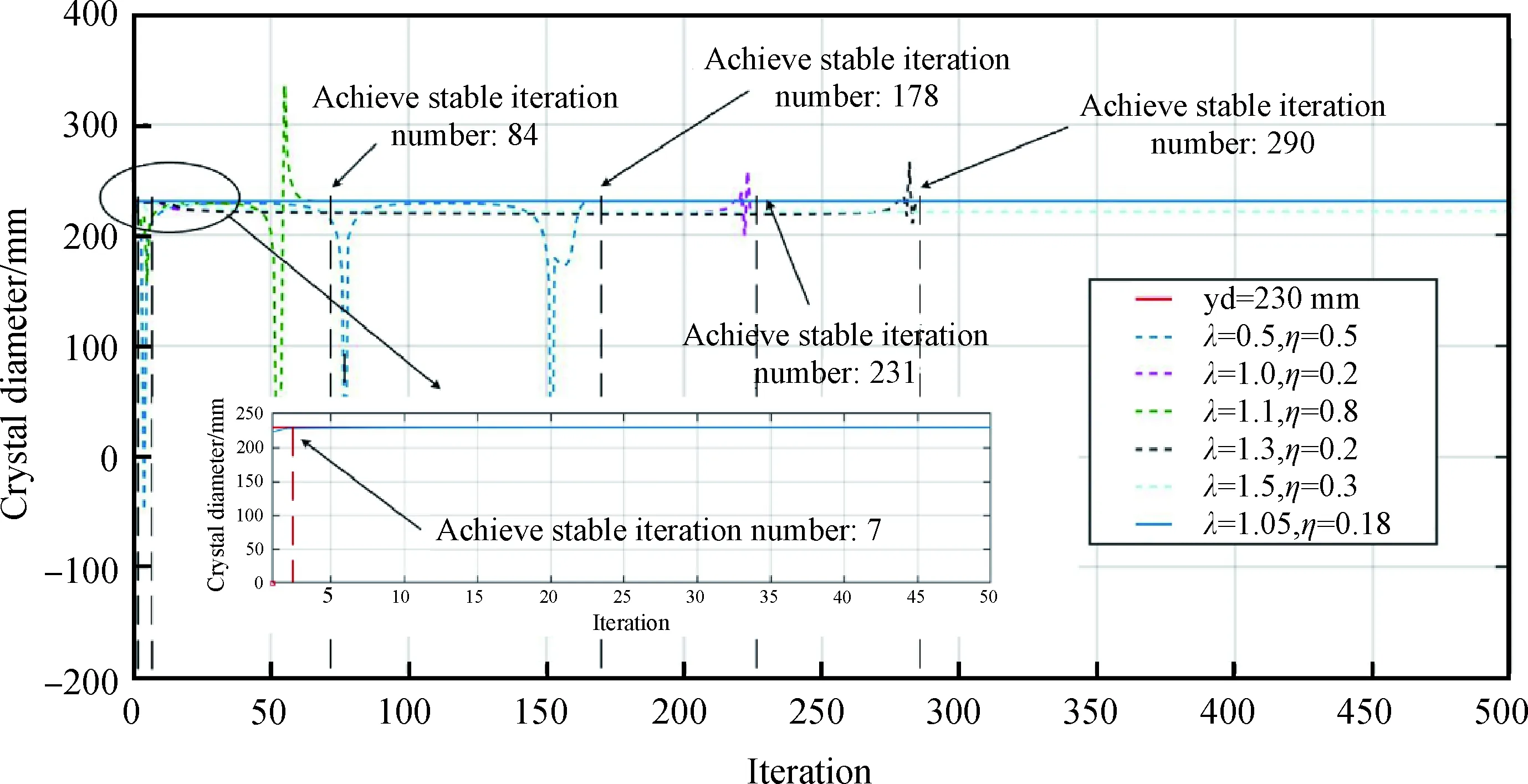
图9 贝叶斯参数优化后的直径控制结果对比Fig.9 Comparison of diameter controlling results after Bayesian parameter optimization
通过图9发现,选取超参数优化区间的最大值进行仿真,迭代次数在7次时,晶体的直径也达到稳定,相对于没有采用超参数优化前的迭代次数减少了245次以上。因此表明采用贝叶斯超参数优化后,MFAC硅单晶直径控制模型降低了计算量,减少了直径控制时间,达到了更好的控制效果。
同时采用贝叶斯优化超参数进行软件仿真后的直径误差和控制输入结果如图10、图11。从图10可以发现,采用贝叶斯对超参数优化后,整个控制过程中的晶体直径误差值最大仅有1.227 6 mm,而最小只有0.168 6 mm,在实际的晶体直径测量中都可以作为测量误差忽略,达到了不错的直径控制效果。同时通过图11对比分析优化前后的控制输入结果发现,在晶体直径达到稳定值之后,控制输入参数u1的最大值为0.215 9 cm/min,最小值为0.161 0 cm/min,而控制输入参数u2最大值为46.623 3 kW,最小值为45.407 2 kW,满足实际晶体生长中坩埚的上升速度在0.1~0.3 cm/min,加热器功率在44~47 kW的合理范围要求,实现了晶体生长过程中工艺参数得到优化的提升,同时降低了生产过程的成本,以较低的加热器功率和较低的坩埚上升速度生产出优质的硅单晶,表明整个控制模型在超参数优下,达到了最佳的直径控制效果。对比贝叶斯超参数优化区间的最小值与最大值发现,晶体直径控制的迭代次数有差异,即控制过程中稳定晶体直径的时长存在差异,选取更小的超参数组合时花费的时间更少,达到稳定直径的过程更快,而值更大的超参数组合达到稳定直径的时间更长。同时超参数的值过小会降低坩埚的上升速度和加热器功率,反之超参数的值更大会适当地增大坩埚的上升速度和加热器的功率。然而,在晶体的生长过程中,更小的坩埚上升速度与加热器功率会增加晶体生在的整体时长,对于批量生产晶体来说,会累计增加生产成本。因此对于不同的生产要求,在控制晶体生长时,应该采用不同的超参数组合里来满足要求。
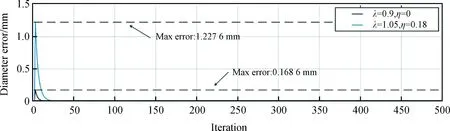
图10 贝叶斯参数优化后的直径控制误差结果Fig.10 Diameter controlling error results after Bayesian parameter optimization
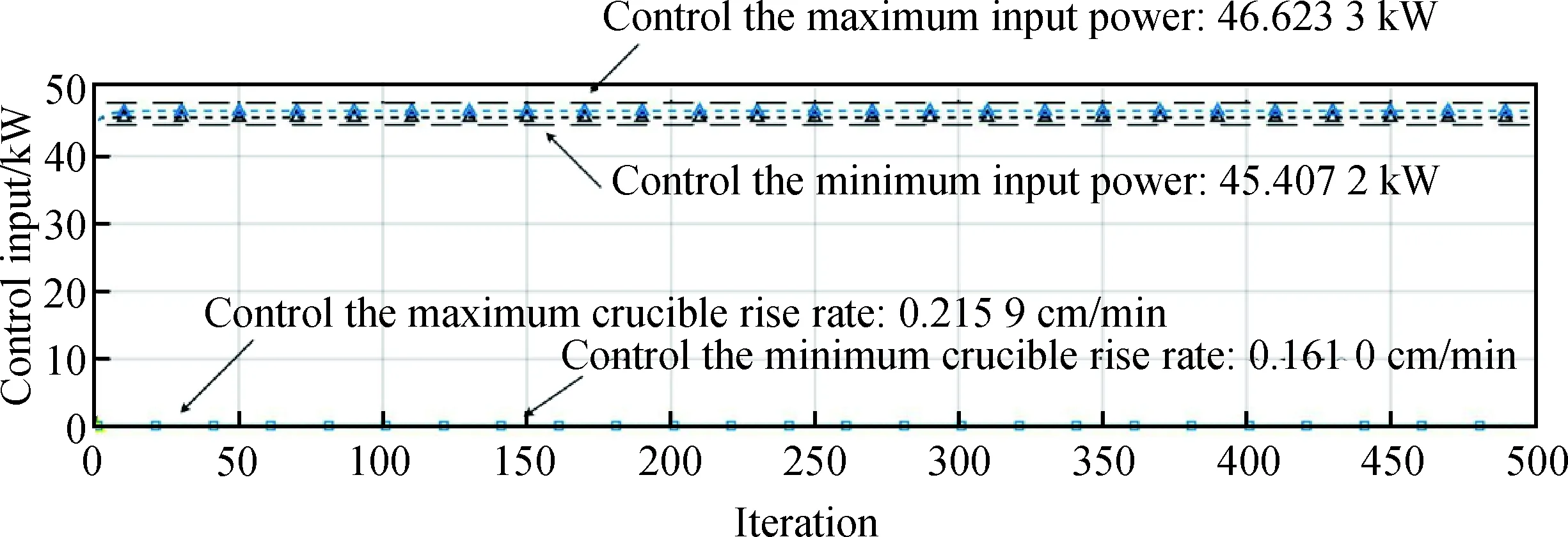
图11 贝叶斯参数优化后的控制输入结果Fig.11 Controlling input results after Bayesian parameter optimization
针对MFAC控制应用于直拉法硅单晶生长过程控制中存在的问题,通过采用贝叶斯参数优化将MFAC硅单晶直径控制算法进行了优化,并重新进行软件仿真,解决了控制过程中存在的计算量和迭代时间的问题,得到了更好的控制效果。表明基于贝叶斯参数优化下的MFAC硅单晶直径控制模型应用于解决晶体直径有不错的效果,不仅将直径控制误差最小降低至0.168 6 mm,同时实现了生产成本的降低。
4 结 论
硅单晶直径的均匀性是影响晶体品质的重要因素之一,如何更好地实现直拉法硅单晶生长过程的直径控制,得到更加均匀的直径一直是晶硅生长领域关注的热点。因此通过分析已有的直径控制方法后,本文提出了MFAC硅单晶直径控制方法。并在根据此控制算法进行软件仿真后发现,控制算法中涉及的超参数对整个控制过程有一定的影响,进而利用贝叶斯参数优化法对超参数进行了优化,确定了超参数的合理范围。对基于贝叶斯参数优化下的MFAC控制算法重新进行软件仿真,验证优化后的超参数有效提高控制效果。MFAC硅单晶直径控制模型解决了机理建模控制和PID控制存在的问题,表现出更好的直径控制能力,而且能够在算法优化后,提高硅单晶生长的稳定性,降低硅单晶生产成本,具有良好的应用前景。
