ZnGeP2晶体中的晶格振动模拟与光谱分析
2022-03-18方声浩
赵 鑫,谢 华,方声浩,庄 巍,叶 宁
(1.中国科学院福建物质结构研究所,福州 350002; 2.天津理工大学功能晶体研究院,天津 300384)
0 引 言
二阶非线性光学材料被广泛地用于诸多领域。如光通信、激光遥感、医学诊断和光电器件等[1-2],其中红外非线光学晶体更是各种军事技术中关键材料,受到各国军方重视[3-5]。目前,具有黄铜矿结构的化合物半导体展现出优异的线性及非线性光学性能,如ZnGeP2(ZGP)[6-7]、AgGaS2(AGS)和AgGaSe2(AGSe)[8-10]。ZGP晶体因具有非线性光学系数大、热导率高、透过范围宽、双折射适宜且机械加工性能良好的特点,被广泛用于各种光学器件中[11-12]。但是,ZGP在9~10 μm存在严重的多声子吸收,严重影响了其在中远红外波段激光输出效率,从而限制其应用性能[13-14]。ZGP晶体中的声子吸收是由晶体中晶格振动引起的,过多的光学吸收不仅会影响晶体的光电转换效率,甚至会导致晶体过热而损坏。
拉曼光谱是一种强大的分析工具,它以非破坏性的方式提供关于半导体材料结构的几个重要方面的有价值信息,如晶格动力学、晶体质量、应变状态、组成或电子结构[15]。为此,通过探究ZGP晶体的红外光学吸收谱和温度与压力依赖的拉曼光谱,可以更好理解晶体结构对于温度与压力的响应以及ZGP晶格振动影响光学吸收的物理机制。同时采用理论计算方式研究变压条件下ZGP晶格振动文献很少提及,因此,本文采用理论计算与实验相结合的方法,研究ZGP晶体中晶格振动与光学吸收。
1 实 验
1.1 晶体生长

图1 ZGP晶体照片Fig.1 Photo of ZGP crystals
本论文中实验所用到的ZGP单晶采用布里奇曼法[16-17]生长得到。按1∶1∶2摩尔比称取高纯(6N,99.999 9%)的Zn、Ge、P并均匀混合后加入石英管中抽真空后封结,采用双温区法合成ZGP多晶原料。将合成的ZGP多晶原料研磨后加入嵌套在直径为22 mm的石英管内并具有自发成核尖端的PBN坩埚中,抽真空至10-3后封管。放入下降炉中,控制坩埚底部位置升温至熔点以上20~30 ℃。恒温24 h后,以0.2 mm/h的速度下降至生长完成。采用同组分ZGP多晶粉末包裹,退火温度580~600 ℃对晶体进行退火热处理,切下数片ZGP晶体,依次用金相砂纸、Al2O3湿粉、金刚石抛光液对晶片进行研磨抛光,直至表面光滑,无明显划痕,如图1所示。
1.2 性能测试
高压和变温原位拉曼光谱实验是在复旦大学光谱实验室完成。光谱系统采用532 nm的固态激光器(HR Evolution (HORIBA)),配有50×长焦镜头(Olympus)和THMS600(Linkam)温控配件。实验样品测试拉曼光谱均在Horiba Labram HR800共聚焦拉曼光谱仪上完成,测试前先完成样品台聚焦,接着用激光完成拉曼信号的校正后设置测试环境参数开始测试,测试用实验样品为两面抛光的ZGP晶片样品。变温拉曼实验中采用银质加热模块,测试温度为80 K、200 K、300 K、350 K、400 K,精度0.1 K,测试激发波长为532 nm,测试范围为80~600 cm-1。高压拉曼实验采用一堆500 μm台面的金刚石砧(DAC),以T301不锈钢作为压砧封垫,封垫的预压厚度为70 μm,初始样品腔直径约为100 μm,压力范围为0~40 GPa。采用体积比为4∶1的甲乙醇作为传压介质,10 μm的红宝石作为压力标定物质。
ZnGeP2晶片的光学吸收谱是通过先将晶体加工为5 mm×5 mm×1 mm的薄片双面抛光后测试其光学透过谱,透过光谱在VEPTEX 70 傅里叶变换红外仪上测试,然后将其透过率转化为吸收系数,转化公式如式(1)[18]:
(1)
式中:Tt为实验所测得的透过率;l为晶体的厚度;T和R为晶体的理论透过率和反射率。关系如式(2)、(3):
(2)
T=1-R
(3)
式中:n0为晶体的寻常光折射率,可由晶体的色散方程得到[13]。
1.3 理论计算
采用第一性原理方法来研究ZGP晶体的晶格振动,并计算了不同压力下晶体的晶格常数和布里渊区中心的振动频率和拉曼位移峰的位置。对于ZGP晶体的电子结构采用密度泛函理论(DFT)计算,晶格动力学采用密度泛函微扰理论(DFPT)计算,使用Quantum Espresso[19]软件包完成上述计算。对于所有计算,平面波的截断能设置为40 Ry,电荷密度截断能设置为320 Ry, k点采用Monkhorst-Pack采样方法并设置为6×6×6。对晶格常数以及原子位置进行几何结构优化,直到体系压力小于0.01×105kPa,原子沿每个方向上的受力小于10-5a.u。采用了广义梯度近似(GGA)中的PBE交换关联泛函并使用了投影缀加平面波(PAW)近似来描述核心电子。对于晶格振动,采用了DFPT方法,并对q点设置为5×5×5,将动力学矩阵采用傅里叶变换得到实空间中的力常数后,沿高对称点和线进行插值得到声子的色散曲线。由于红外吸收和拉曼散射主要由布里渊区中心的晶格振动决定,所以在不同压力下的晶格振动主要计算了布里渊区中心的振动频率。
2 结果与讨论
2.1 ZGP晶体红外吸收

图2 ZGP晶体的红外吸收光谱Fig.2 Infrared absorption spectrum of ZGP crystal
ZGP晶体3~24 μm的红外吸收光谱如图2所示。从图中可以看出,ZGP晶体在8.95 μm处存在一个较弱的吸收峰,在12~13 μm,ZGP晶体的吸收系数急剧增加,并在12.89 μm处出现透过截止。通过分析拉曼散射和声子色散谱的能量,ZGP声子光学纵模的最高振动频率为398 cm-1,对应波长为25.13 μm,可知12.56~25.13 μm的吸收主要由于双声子的吸收引起,在12 μm附近的吸收为双声子吸收的截止带边。文献报道ZGP晶体在8.95 μm处的吸收峰是由晶格振动引起的[20-21],其为多声子吸收,吸收强度相比双声子吸收要弱得多。为了进一步研究ZGP晶格振动与光学吸收的物理机制,测试并分析了ZGP晶体变温拉曼和变压拉曼光谱。
2.2 ZGP晶体振动模对称性
ZGP晶体为黄铜矿结构化合物,属于I-42d(D2d12)空间群,晶格常数a=b=0.546 5 nm,c=1.070 8 nm,α=β=γ=90°。一个ZGP晶胞中包含4分子,共有8个离子,体心单胞中重复单元为2,因此ZGP晶体具有24种基本晶格振动模数。D2d12空间群在考虑到简并情况时能产生的17种简正振动模式为:Г= 1A1(R)+2A2+3B1(R)+4B2(R,IR)+7E(R,IR),其中本Г为光学模,A1、A2、B1和B2非简并光学模,E为二重简并光学模[22]。R和IR分别是拉曼和红外活性。根据D2d点群的特征标表,理论上可以观测到13个拉曼振动模,但是实验中由于仪器设备灵敏度以及晶体内部的缺陷结构等其他原因,有一些峰无法测得,因此测得的拉曼峰的数量比较少,所以ZGP晶体的一些拉曼振动模可以通过拉曼散射效应测试得到,如表1所示,其中E模是二重简并模。与拉曼光谱不同,ZGP晶体的红外吸收谱是光学吸收谱,其中的吸收峰可能是由两个或多个振动模同时作用引起多声子吸收造成的。

表1 理论计算与实验的拉曼峰的位置Table 1 Calculated and experimental position of the Raman peak
2.3 变温拉曼分析
一束单色光入射于试样后有一部分会被散射。散射光中的大部分波长与入射光是相同的,而一小部分由于试样中分子振动和分子转动的作用,使得波长发生偏移,这种波长发生偏移散射就是拉曼散射,分为斯托克斯散射和反斯托克斯散射。拉曼峰峰值位置可以由洛伦兹线型拟合得到,晶体中拉曼位移的温度特性主要由热膨胀或体积变化导致的振动频率改变,不仅如此,其线宽、强度都会随温度的变化而变化。斯托克斯与反斯托克斯散射的机理不同,二者随温度的变化趋势相反,在同一入射光源和同样的采集时间下,斯托克斯峰随着温度的升高而降低,而反斯托克斯峰会升高[23]。
拉曼峰位置会随温度的变化而变化,拉曼频率的温度特性可以由公式(4)描述[24]:
ω(T)=ω0-C1T-C2T2
(4)
式中:ω0为0 K温度下的拉曼位移;C1和C2分别为一级和二级温度系数。从公式中可以看出,随温度升高,拉曼峰会向低频移动。
Klemens理论[25]认为拉曼光学声子会衰变成属于同一分支的两个声学声子,且拉曼峰的半峰全宽的温度依赖性可以表示为:
(5)
式中:Г0为0 K时位于频率为ωB的拉曼峰的半峰全宽;h为普朗克常数;kB为玻尔兹曼常数;ωB为特征频率。所以,一般来说,拉曼峰的半峰全宽会随温度的升高而变大。
图3为ZGP在不同温度下(80~400 K)的拉曼光谱。随着温度的升高,ZGP晶体中拉曼散射强度减弱,半峰全宽变大,且拉曼频率发生红移。温度升高,ZGP晶体中的晶格振动加强,原子间相互作用力增强。同时由于热膨胀效应导致晶格常数产生变化。由于变温拉曼测试过程中所用激发光源波长为532 nm,所以在100~500 cm-1范围内的拉曼散射属于斯托克斯,随着温度的升高,斯托克斯峰随着温度的升高而降低,这是因为随着温度升高,声子数目变多[26],发射声子的几率降低,且高温下拉曼光谱的噪声信号比较强,所以随着温度升高,100~500 cm-1范围内的拉曼散射强度降低。不仅如此,由公式(4)和(5)可知,随温度升高,ZGP晶体的半峰全宽变大,拉曼峰红移,这是由频率的温度特性决定的,也说明温度升高,ZGP晶体晶格振动恢复力减弱。ZGP拉曼光谱的主要峰位于143 cm-1、330 cm-1、348 cm-1、371 cm-1、389 cm-1和398 cm-1处(见表1),对于ZGP晶体在8.95 μm处由于晶格振动引起的吸收,对应波数为1 117 cm-1,可能是由B2(348 cm-1)、E(371 cm-1)和B2(398 cm-1)三个声子的和频振动吸收造成。图4为温度依赖ZGP的拉曼声子频率,可以看出温度与多个拉曼模频率存在类似于线性依赖的关系,这进一步说明了ZGP晶体中晶格振动随着温度升高而增强,并使得其拉曼模发生红移。

图3 温度依赖的ZGP的拉曼光谱Fig.3 Temperature evolution of Raman spectra of ZGP

图4 ZGP各拉曼模的频率随温度的变化Fig.4 Raman frequency of ZGP varies with temperature
2.4 加压拉曼分析
图5为ZGP晶体的高压拉曼激光谱,低于28 GPa时拉曼峰蓝移,高于28 GPa开始红移,得知晶体在28 GPa时发生相变,说明晶体在24 GPa下是力学稳定的[27]。由图可知,高压下各个拉曼模发生了蓝移,这是由于在外界压力的作用下,晶体内部原子相应地受到应力的作用,使得各个原子之间的相互作用力增强,ZGP晶体中各原子键长缩短,原子间振动增强,晶格常数发生微弱变化。不仅如此,与变温拉曼谱类似,随着压力增强,拉曼峰强度降低,半峰全宽变大。ZGP拉曼光谱的主强峰位于143 cm-1、330 cm-1和398 cm-1处,这些振动模属于“压缩模”,反映了ZGP晶格的整体振动。在变压拉曼谱中,未测得330~398 cm-1间的拉曼峰,这是由变压拉曼与变温拉曼测试中的实验条件不同导致的。ZGP中观测到的拉曼特征的压力依赖关系如图6所示,可以看出压力与各拉曼模频率是近似的线性依赖关系,因此可用关系式ωi(P)=ωi(0)+aiP来拟合其线性关系,其中ωi(0)和ai分别表示第i模的零压力频率和压力系数,拟合得到的结果如图6所示。基于这个关系,ZGP晶体中9~10 μm处由晶格振动的吸收可以通过施加压力来使得吸收位置发生蓝移,这一结果可为ZGP晶体在中远红外的应用提供参考价值。

图5 压力依赖的ZGP的拉曼光谱Fig.5 Pressure evolution of Raman spectra of ZGP
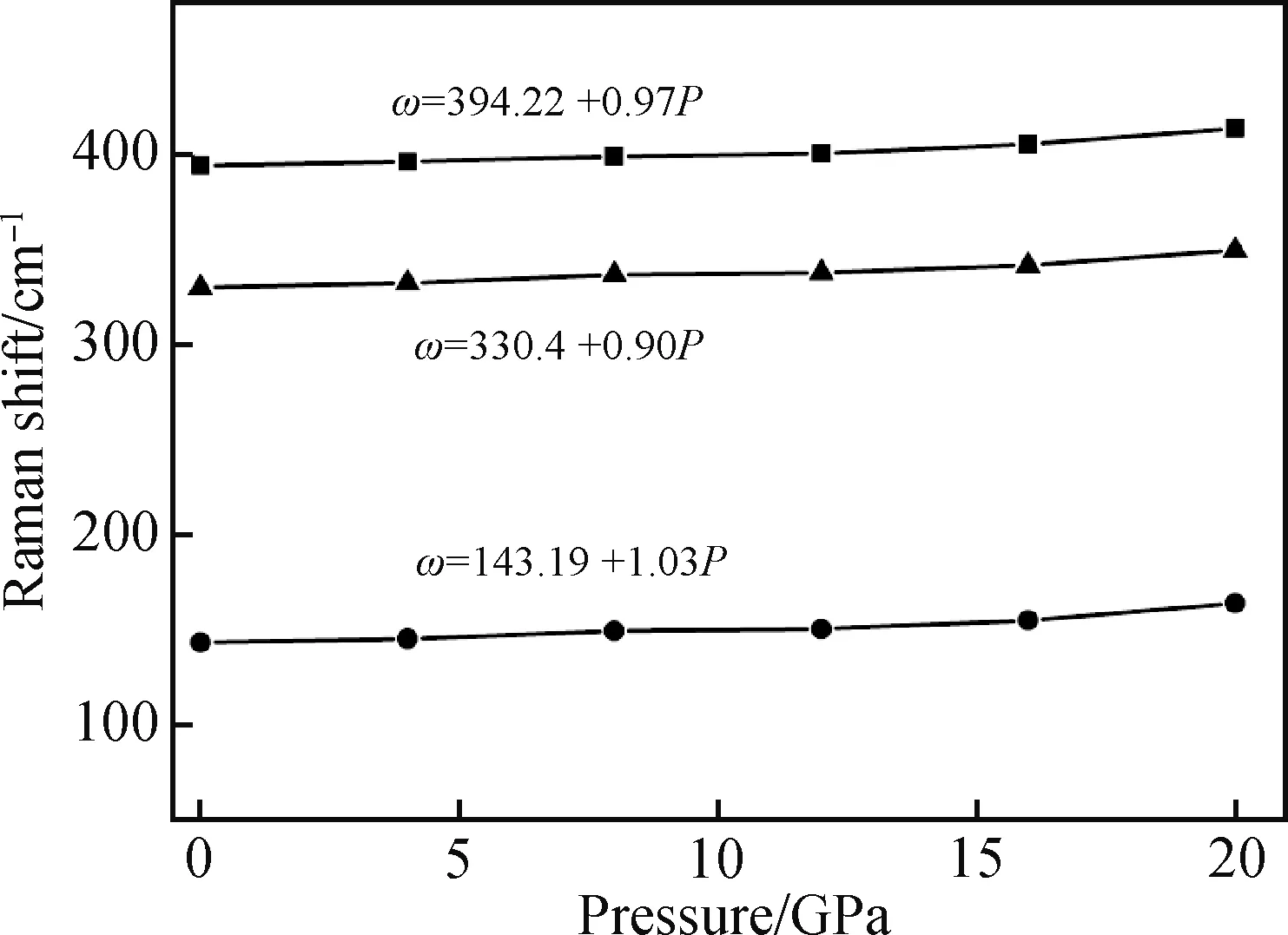
图6 ZGP各拉曼模的频率随压力的变化Fig.6 Raman frequency of ZGP varies with pressure
2.5 多声子吸收谱
通过拉曼散射和声子色散谱的能量,ZGP声子光学纵模的最高振动频率为398 cm-1,对应波长为25.13 μm,可知12~24 μm的吸收主要由双声子的吸收引起,8.95 μm的吸收由多声子吸收引起。其中12.89 μm的红外吸收截止边是由频率为398 cm-1的光学纵模声子的倍频吸收引起。在变温拉曼分析中,推测ZGP晶体在8.95 μm处吸收可能是由B2(348 cm-1)、E(371 cm-1)和B2(398 cm-1)三个声子的和频振动吸收造成的,为了进一步研究ZGP晶体在8.95 μm处吸收与声子振动模的关系,基于第一性原理计算了ZGP晶体的声子色散谱。每个ZGP原胞中包含8个原子,因此在声子色散谱中包含24个分支,其中3条声学支和21条光学支。图7为采用DFPT计算得到的沿第一布里渊区高对称线[28]的声子色散谱。通过晶体对称性分析,对于Gamma点光学声子,A1和B1模式具有拉曼活性,B2和E模式同时具有拉曼和红外活性。由声子色散谱中没有虚频可知,ZGP在I-42d空间群下具有动力学稳定性。通过声子色散谱可以看到,对于光学支声子,其能量分布在三个区间,分别为振动频率在300~375 cm-1的高频区,175~225 cm-1的中频区以及75~135 cm-1的低频区。为了了解不同的晶格振动模式对拉曼光谱以及红外吸收光谱的影响,对比拉曼光谱测出的Г点的频率与理论计算的结果,结果如表1所示。通过对比,在低频部分,理论结果与实验结果相差5 cm-1左右,在中频部分,相差10 cm-1左右,在高频部分,相差20 cm-1左右。理论与实验频率的差距来源于晶格常数的差异以及理论计算中对于核心电子采用了赝势,会对力常数的计算引入误差。而且理论计算的误差主要在高频部分出现。
在实验测的红外吸收谱图中发现,在9 μm附近会存在明显的吸收,其吸收峰的位置在8.95 μm,对应的波数为1 117 cm-1。通过分析电子带隙[28]和声子谱发现,该吸收峰由多声子吸收引起,且至少为三声子吸收。通过分析声子在Г点的频率和红外活性,发现9 μm附近的吸收由B2(3 48 cm-1)、E(371 cm-1)和B2(398 cm-1)三个声子的和频振动吸收引起。因此通过分析这三个振动频率随压力的变化,则可以知道9 μm的红外吸收频率随压力的变化。
2.6 晶格动力学随压力的变化
ZGP晶体在9 μm附近的红外吸收会引起非线性光学性能以及发热的问题[29-30],其吸收起源于晶体本征的晶格振动,因此无法将其消除。而通过对晶体掺杂重原子或者改变其晶格常数可以改变晶格振动的频率,可以将红外吸收的区域移除出大家较关心的频率区域。而掺杂重原子会改变晶体的对称性并在电子能带中引入缺陷能级,这将影响ZGP晶体的非线性光学性能并引入新的吸收区域。因此本文通过加压改变晶体的晶格常数,来调控晶格振动的频率。
通过对ZGP晶体加上各向均匀的压力,并采用第一性原理优化其晶格常数和原子受力,其收敛判据如前所述。计算得到的晶格常数a以及晶体的密度如图8所示,其中沿z方向的晶格常数与x方向的晶格常数的比值c/a随着压力变化维持在1.972附近。在0 GPa时,晶格常数a=0.549 1 nm,实验结果为0.546 5 nm,其误差来源于实验是在大气压下测量的。随着压力从0~30 GPa的变化,晶格常数a从0.549 1 nm变化到0.507 6 nm,晶体密度从4.067 g/cm3变化到5.152 g/cm3。而晶体对称性未发生改变,因此在一定压力下加压,晶体不会发生相变,也不会对非线性性能产生影响。

图7 理论计算的ZGP晶体的声子色散谱Fig.7 Calculated phonon dispersion spectra of ZGP crystal

图8 ZGP晶体在不同压力下的晶格常数和密度Fig.8 Lattice constant and density of ZGP crystal under different pressures
在Г点处不同的振动频率随压力的变化如图9所示,通过对频率和压力进行线性拟合,其关系如图9中关系式所示。计算出来的拟合系数与实验值上存在一定的差异,这是由于理论计算对应的压力为各个方向上的均匀压力,而实验加压为某一特定方向上的压力。通过前述分析可知,9 μm附近的吸收由A5, A6和A8三个声子的共同吸收引起,这三个振动模式的频率与压力的关系如下:ω(A5,P)=334+4.07P,ω(A6,P)=356.3+4.18P,ω(A8,P)=384.02+4.32P,其中频率单位采用cm-1,压力单位采用GPa。则9 μm附近的吸收峰与压力的关系为ω(Peak,P)=1 074.32+12.57P。其吸收峰随压力的变化如图10所示。

图9 Г点声子频率随压力的变化Fig.9 Г point phonon frequency under different pressures

图10 理论预测9 μm附近的吸收峰随压力的变化Fig.10 Theoretical prediction of the absorption peak near 9 μm changes with pressure
3 结 论
本文解释了ZGP晶体红外截止边和9 μm附近吸收峰的物理机制:ZGP晶体在9 μm附近的吸收是由B2(348 cm-1)、E(371 cm-1)和B2(398 cm-1)三个声子的和频振动吸收造成的,吸收强度相比双声子吸收要弱得多,12.56~25.13 μm的吸收主要由于双声子的吸收引起,在12 μm附近对应的是B2(398 cm-1)双声子倍频吸收的吸收峰的截止边。变温拉曼光谱和光学吸收谱研究表明,在80~400 K之间,温度升高使得其拉曼峰发生红移,与此同时,其拉曼峰强度减弱,半峰全宽变大。压力升高则会引起ZGP晶体的晶格常数减小,晶格振动模发生蓝移,其振动模强度减弱,半峰全宽变大。ZGP晶体在9 μm附近吸收是本征晶格振动引起,无法消除,为了减少ZGP晶体在应用的过程中的晶体振动以及由晶格振动引起的光学吸收以提高晶体的应用性能,可以设计合适的变温或者变压装置来改善ZGP晶体在9 μm附近的吸收。
