压电超材料主动控制分流电路设计
2022-03-16王勋宝付宝伟
李 泽,王勋宝,刘 钊,倪 明,付宝伟
(上海机电工程研究所,上海 201109)
0 引言
随着现代科学技术的日益发展和武器系统复杂度的不断增加[1],如何有效地解决工程领域中出现的振动问题已受到了广泛的重视。声学超材料[2]凭借其独特的带隙特性为振动/噪声控制贡献了新的思路,在低频隔声或减振[3-4]和声学隐身[5-8]等领域有着极大的应用前景。
本文研究了压电超材料分流电路数字控制器的设计方法,通过分析分流电路作用下压电片等效弹性模量的零极点特征,提出了一种适用于超材料传递函数零极点配置的方法,从而实现对超材料带隙的灵活控制。所提出的零极点配置法无需进行复杂的模拟和数字阻抗分析,可以直接根据共振频率选择合适的零极点进行传递函数的设计,进而通过微控制器灵活地控制带隙,这一优势有助于智能超材料的研制。
1 声学超材料周期梁结构模型分析
将接有分流电路的压电片周期性地粘贴于均质梁上,在材料和结构周期共同作用下,结构会产生振动带隙,压电超材料结构梁如图1所示。

图1 压电超材料结构示意图
图1中的压电超材料结构元胞主要由以下3部分组成:
1) 粘贴有压电片的基体梁结构(见图1中A),长度为lA。
2) 未贴压电片的基体梁结构(见图1中B),长度为lB。
3) 图1中的分流电路,电路阻抗用Z表示。
若将压电片和梁段结构贴合紧密,则压电片对结构动力学特性的影响可忽略。下面针对该结构的弯曲振动带隙特性进行分析。
压电片a和b的压电方程分别为
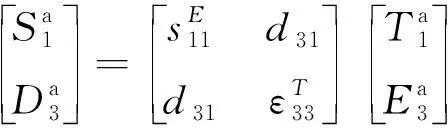
(1)
(2)
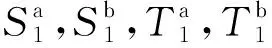
(3)
Ep为压电片的等效弹性模量,则压电片a的等效弹性模量为

(4)
对于压电片b,由式(2)可得:
(5)

(6)
根据电学相关知识,分流电路中电流为
(7)
式中:s为Laplace算子;Q为电荷量;V为压电片电极上的电势差。
压电片电极上的电势差与电场强度的关系为
(8)
式中hp为压电片的厚度。
将式(8)代入式(7)可得:
(9)
假设压电片内应变和电极上电位移近似相等,则电极上的Q可表示为
(10)
式中Ap为压电片的横截面积。
联立式(5)、(9)和(10)可得压电片b内电场与应变的关系为
(11)

(12)
将式(11)代入式(2)可得压电片b应力与应变之间的关系为
(13)
因此,在长波假设法下,外部分流电路的影响可等效为结构弹性模量发生了变化,电路作用后压电片b的等效弹性模量为
(14)
2 基于零极点配置的主动控制分流电路
基于零极点配置的主动控制分流电路结构示意图如图2所示,该电路主要由电荷放大器、模数转换器(ADC)、微控制器、数模转换器(DAC)和比例放大器组成。图中,C1为电荷放大器的电容,RA、RB为同向比例放大器的两个电阻。

图2 主动控制分流电路结构示意图
图2中,压电片a为传感器,可以将结构应变转换成电信号,作为分流电路的输入信号,输入信号通过电荷放大器转换成电压信号V1,再由ADC进行数字化处理,然后通过微控制器输出控制信号,再经由DAC转换成模拟电压信号V2,最后将经过比例放大器放大后的电压信号施加给作动压电片b。

(15)
施加在作动压电片b上的电压为
Vout=βV2
(16)
式中β=(RB+RA)/RA为同向比例放大器的放大倍数。
假设嵌入微控制器的传递函数H(s)=V2/V1,则每个元胞的输入、输出之间的传递关系为

(17)
其中:

(18)


(19)
参考复合梁的形变特性,上下对称粘贴的压电片所产生的应变符合大小相等、方向相反的规律,因此:
(20)
结合式(20)可得压电片b的等效弹性模量为
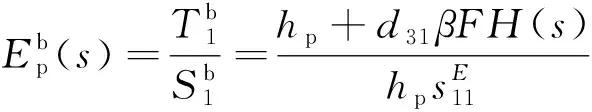
(21)
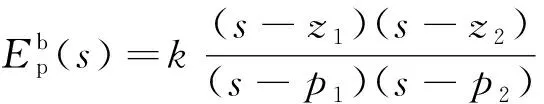
(22)
式中:z1,z2为传递函数的零点;p1,p2为传递函数的极点;k为增益。
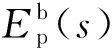
η=real(z1,2)=real(p1,2)
(23)
已知每对共轭极点代表一个共振模态,因此极点的虚部imag对应输出响应的共振角频率,即:
imag(p1,2)=2πfosc
(24)
由式(22)可知零点的实部已确定,已知传递函数的零点并不影响自由运动的模态,但是会影响各模态在响应中所占的比重。因此,通过调节虚部可确定零点的位置。
imag(z1,2)=±λimag(p1,2)
(25)
式中λ为电路设置的一个参数。
3 仿真与实验结果分析
搭建的实验平台如图3所示,其中压电超材料结构主体部分由基体梁和粘贴在基体梁上的6个压电共振单元组成,每一个压电共振单元都是由相同的压电片和分流电路组合而成,以保证压电超材料的周期性。
其中梁结构采用铝合金材质。将整个超材料结构梁用绳子悬挂起来以创造自由边界的条件。激振信号由函数发生器产生,然后经由功率放大器放大,最后施加在激振器上,激振器在试样的左端进行激励。梁结构两端的振动加速度由两个加速度计进行测量,经过电荷放大器将信号转换成电压信号并进行放大,电压信号与加速度成正比。得到的试样两端振动加速度值通过数采卡送至控制器用以信号采集。最后通过计算机对振动响应的所有振幅和相位数据进行处理,从而得到测试试样从左到右的振动传输特性曲线。分流电路中的运放采用直流电源进行供电。
对主动控制分流电路按照表1进行参数设置,图4为主动控制分流电路作用下压电超材料的传输特性仿真曲线和实验曲线。图中黑色实线表示所有元胞压电片在短路时声学超材料的振动传输特性曲线,可以作为参照曲线。

表1 电路参数

图4 分流电路作用下压电超材料的传输特性曲线
由图4(a)可知,按照表1进行参数设置可以在第二、三、四阶低频模态处产生明显的振动衰减效果。在图4(b)中,结构在210 Hz、430 Hz和720 Hz模态处的振动衰减幅度分别为14 dB、15 dB和20 dB,由此说明主动控制分流电路作用下的压电超材料可以产生有效抑制结构振动的控制带隙。
4 结束语
本文通过压电超材料的结构模型分析,提出了一种可以直接通过调节极点和零点设计弹性模量传递函数的方法,并通过仿真与实验阐述了零极点位置对超材料带隙的影响。所提出的主动控制分流电路可以通过计算机调控相关参数,无需手动调整电感,控制过程更简单灵活。这一优势有助于智能超材料的设计。
