基于快速傅里叶变换的SmaartLive音频测量基本原理（节选）

Paul+D.+Henderson

【摘 要】 介绍关于SIA-SmaartLive?测量平台上所使用的快速傅里叶变换（FFT）技术性实践分析报告的概况，从而了 解SmaartLive基于FFT测量的基本概念，进而理解其测量参数、步骤以及所得数据。

【关键词】 音频测量；SmaartLive；快速傅里叶变换；传递函数；脉冲响应

文章编号： 10.3969/j.issn.1674-8239.2017.01.004

The Fundamentals of FFT-Based Audio Measurements in SmaartLive

Original/[USA]Paul D. Henderson Translate/HE Kai-chen1， JI Xiang1

（1. The Communication University of China， Beijing 100024， China）

【Abstract】This article serves as summary of the Fast-Fourier Transform （FFT） analysis techniques implemented in the SIA-SmaartLive measurement platform. By reading through this document， you will receive an understanding of the fundamental concepts in FFT-based measurements， providing you with insights to better comprehend the measurement parameters， procedures， and resulting data.

【Key Words】audio measurement； SmaartLive； fast fourier transform； transfer function； impulse response

本文是关于SIA-SmaartLive? 测量平台上所使用的快速傅里叶变换（FFT）技术性实践分析报告的摘要。通过阅读这一文章，将会了解到SmaartLive基于FFT测量的基本概念，进而对测量参数、步骤以及所得数据有更好地理解。

1 时域采样：将信号送入SmaartLive

一般来说，声信号和电信号都是连续的，它们在每个时间点上都有一个确定的值，故可以使用测量仪器来测量声压和模拟电压这类连续信号。然而，为了能够通过SmaartLive这种基于计算机的测量系统来分析这些连续信号，必须把它们转换为一系列数字样本，且每个数字样本能够代表一个在特定时间点上与被测信号成一定比例的有效数值。这一过程被称为采样：即把时间上连续的信号转换为时间上分离的信号。

用于SmaartLive测量（及其他数字音频应用）的采样过程在均匀间隔的时间点上产生数据。每秒的采样数值就是大家熟悉的采样率，缩写为SR（Sample Rate），单位为Hz。采样率直接影响计算机中能够分析的最高频率，即“尼奎斯特限定频率（fmax）”，它等于采样率的一半。对于电声信号和电声系统的测量，通常信号所处的频段约在20 Hz到20 kHz之间。因此，在大部分的测量中，最好选择声卡和SmaartLive能够同时兼容的最高采样率。一般情况下，48 kHz和44.1 kHz都能够提供一个至少为20 kHz的测量带宽。

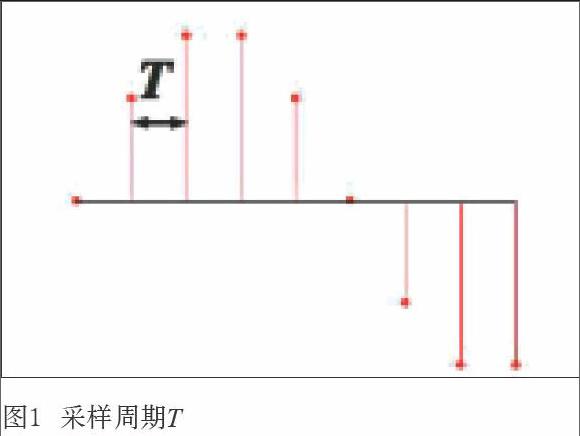
采样周期是一个与采样频率反相关的参数，它表示的是采样之间的时间间隔（以s为单位），测量精度在时间上与采样周期T相等，见图1。这就意味着不能从持续时间短于这个精度的信号中分辨出任何的细节。例如，如果利用SmaartLive，通过寻找脉冲响应峰值的方法来测量信号延时，则无法测得小于T的延时量。

除了选择理想的采样率之外，在设置测量系统时也必须要考虑模数转换器的字长。对于每一个采样而言，模数转换器必须指定一个确切的数字比特模式来代表其振幅。实际上，模数转换的字长越长，或每个采样的比特数越长，测量的动态范围就会越大。更为重要的是，字长的增加会提高所测量振幅精度，因为信号振幅上的采样点被分配在了更小的间隔中。与采样率相同，在保证与硬件兼容的前提下，应将SmaartLive中的字长设为最大值。

2 FFT分析：观察频域信息

虽然在部分情况下，在时域进行测量是很实用的，但是大多数的音频测量需要频谱信息，了解音频信号及整个系统的频率内容和特征。幸运的是，目前已经存在一个特定的技术将数据从时域转换到频域。傅里叶变换能够将一个时序信号转换为复杂的频域信息，它包含了构成信号的正弦波分量的振幅和相位信息。另外，傅里叶变换提供了一个反向变换，在不丢失任何信息的情况下，把复杂的频域信号数据转换为时域信号。所以，时域数据和频域数据是相同的：它仅仅提供了观察同一信号的不同视角，详见图2。

3 傅里叶理论

19世纪，法国数学家Jean Baptiste Joseph Fourier 提出一个概念，把任何时间信号表达为若干基本频率的函数。傅里叶理论认为，任何复杂的时序信号，无论是噪声、语音还是音乐，都可以看作是一系列不同频率、振幅和相位的正弦波的组合。有了这一基本概念，可以通过数学的方式将信號在时域和频域之间进行转换。

为了把连续信号x（t）转换为它所对应的频域X （jw），用到前面提到的傅里叶变换：

（公式1）

也可以通过反向傅里叶变换，在不丢失任何信息的情况下将上述过程进行逆向转化：

（公式2）

值得注意的是，在最为严格的条件下，傅里叶变换需要一个完整的时间历史（无限长的时间）和无限数量的正弦频率分量来充分地描述一个信号。显然，这对于测量来说并无实际意义。为了利用计算机来进行傅里叶变换，必须使用时间窗将对信号的观察限制在一个有限的时间范围内。这是基于采样信号数据运行的离散式傅里叶变换（DFT：Discrete Fourier Transform），或通过计算机运算的离散式傅里叶变换，即快速傅里叶变换（FFT： Fast Fourier Transform）。