基于深度神经网络(DNN)的压电陶瓷前馈补偿研究

熊永程,贾文红,张丽敏,郑丽芳

(1.中国科学院 上海应用物理研究所,上海 201800;2.中国科学院大学,北京 100049;3.中国科学院 上海高等研究院,上海 201210)

0 引言

在同步辐射装置中，从储存环引出的同步光经单色器真空腔内两块晶体衍射后成为用户实验单色光。单色器第二晶体俯仰角是调节两块晶体保持平行、获得优质光斑的关键部件，要求其运动机构具有响应快，精度高及噪声小等特点，同时由于单色器内部空间狭小，故而其必须体积小，运动灵活，为此常应用压电陶瓷驱动器来实现，运动精度为微米量级。为了获得实验要求的优质同步光斑，在光束线调束优化过程中，线站人员根据电离室读数和电荷耦合器件(CCD)探测出光斑形状，不断地调节俯仰角和其他运动机构，整个过程需要大量时间[1]。

每年运行近5 000 h的上海同步辐射光源具有海量的数据资源，数据的高可用性为人工智能技术在同步辐射领域的应用带来巨大机遇。近年来,上海同步辐射光源开展了基于差分进化算法的智能光束线的探索并取得初步成功[2]。然而在智能调束过程中，研究人员发现引入单色器第二晶体俯仰轴后，由于其运动重复性差，优秀个体遗传到下一代失效，导致智能算法不收敛。影响俯仰轴运动重复性的因素有压电陶瓷固有的迟滞非线性、蠕变属性等。在不考虑振动引起的误差下，迟滞引入的不确定性一般为15%～20%，蠕变误差为1%～5%[3]。

压电陶瓷迟滞非线性特性及补偿技术一直是国内外学者的研究热点[4-6]。早期的经典前馈控制技术是应用数学方法建立迟滞回线的拟合模型，通过求解其逆模型，得到激励电压与实际输出位移的关系[7-9]。由于迟滞回线非线性特性复杂，尽管学者们提出了如Preisach模型、Bouc-Wen模型、Maxwell模型、多项式模型等数学模型，但其对迟滞回线的描述均存在一定局限性，因而一直是未被广泛认可的通用模型。

神经网络可用于拟合任意非线性曲线[10]，且具有泛化能力，理论上用神经网络拟合迟滞曲线是可行的。本文将压电陶瓷主迟滞回线和次迟滞回线作为深度学习的训练数据集，在PyTorch框架下经100 000轮训练，将得到的深度神经网络迟滞模型应用于压电陶瓷驱动器的前馈补偿。测试结果表明，应用前馈补偿后，被控滑台的运动位移精度从开环状态下的约8.91 μm提高到近80 nm，系统响应带宽100 Hz，可以应用到智能调束系统单色器俯仰角的前馈控制中。

1 压电陶瓷迟滞回线

压电陶瓷迟滞非线性主要表现在输入电压与输出位移的对应曲线上。电压上升与电压下降时的曲线不重合，影响这一特性的因素不仅与当前的输入电压有关，还与输入历史和输入信号频率等有关[11]。

本实验采用Physik Instrumente(PI)公司的E-709.CRG压电陶瓷控制器及P-621.1CD压电陶瓷微位移台，控制器中集成了信号放大器，位移台内集成了电容传感器。控制器接收命令后，通过信号放大器将电压发送给位移台，并从电容传感器回读压电陶瓷当前位置，向上通过USB与计算机通信，如图1所示。

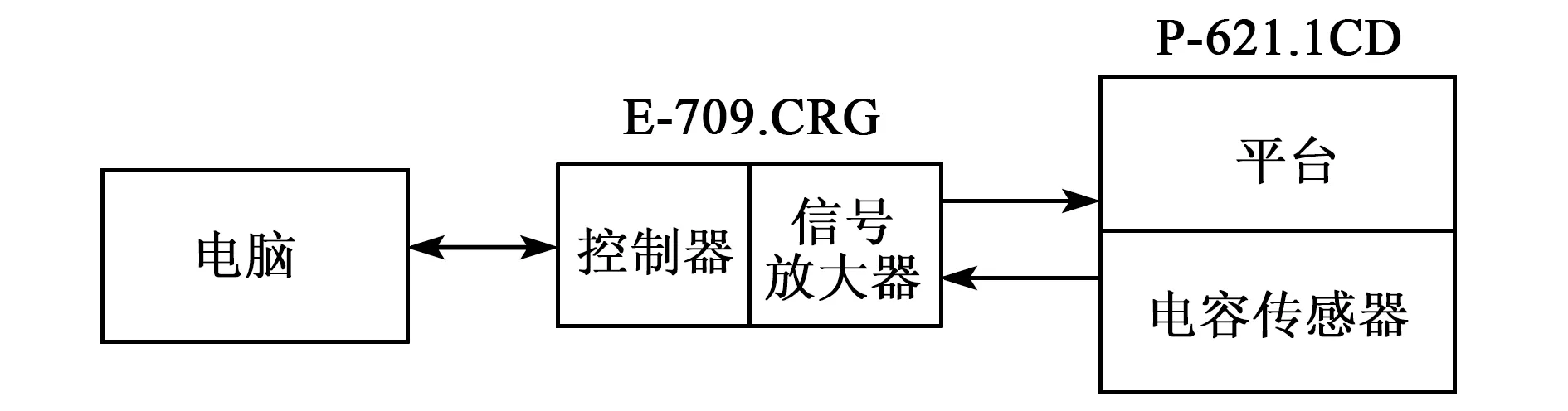
图1 实验平台通信图

1.1 主迟滞环

输入信号频率为10 Hz，步长0.1 V。升程曲线测试范围为-5～107 V，回程曲线测试范围为107～-6 V。以输入电压(V)为水平轴，输出位移(x)为垂直轴，得到位移台的主迟滞环。

对主迟滞环进行线性拟合，得到x与V的线性关系为

x=0.976 579 417 023 688 6V+

0.274 239 524 880 049 05

(1)

图2为升程曲线和回程曲线与拟合直线的偏差，升程曲线的最大偏差出现在107 V处，为-4.97 μm；回程曲线的最大偏差出现在40 V处，为8.91 μm。

图2 主迟滞环线性分析结果图

1.2 次迟滞环

当输入电压为减幅正弦信号或增幅正弦信号时，压电陶瓷的输入电压与输出位移曲线呈现类似螺旋线的不相交迟滞环状态，即次迟滞环。图3、4分别为减、增幅正弦输入信号时次迟滞线性分析结果图。微位移台对减、增幅正弦信号具有一定跟踪能力，但是误差比简单运动模式(步进运动)更大，对这两种信号跟踪的最大误差均在6 μm左右。

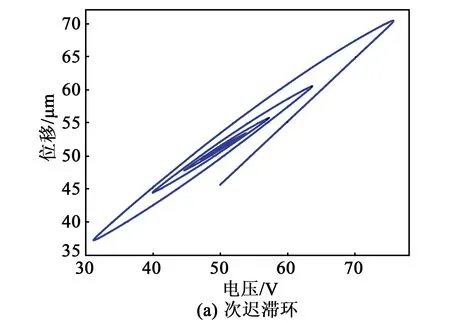
图4 增幅正弦输入信号的次迟滞环线性分析结果图

从图2～4可发现，滑台当前位置与当前输出电压、上一次位移和上一次输出电压有关，即假定：

xt=f(Vt,xt-1,Vt-1)

(2)

式中：xt为当前t时刻的位移；Vt为当前t时刻的输入电压;Vt-1为上一位移的输入电压;xt-1为上一位移。

经变换后可得：

Vt=f′(xt,xt-1,Vt-1)

(3)

将参数修改后可得：

VR=f′(xT,xt-1,Vt-1)

(4)

式中：VR为所需输入的电压；xT为给定的目标位移；f′为由神经网络需要构建的函数关系。

对于压电陶瓷位移台，由给定目标位置、上一位置输入电压、上一位置位移，通过函数f′计算得到施加到压电陶瓷的电压值。

本文设计了一个基于深度神经网络的前馈控制模型，对预先设定的目标位置进行补偿计算，将结果经控制器输出并施加给压电陶瓷，实现微位移台运动至目标位置，图5为整个系统的原理结构图。

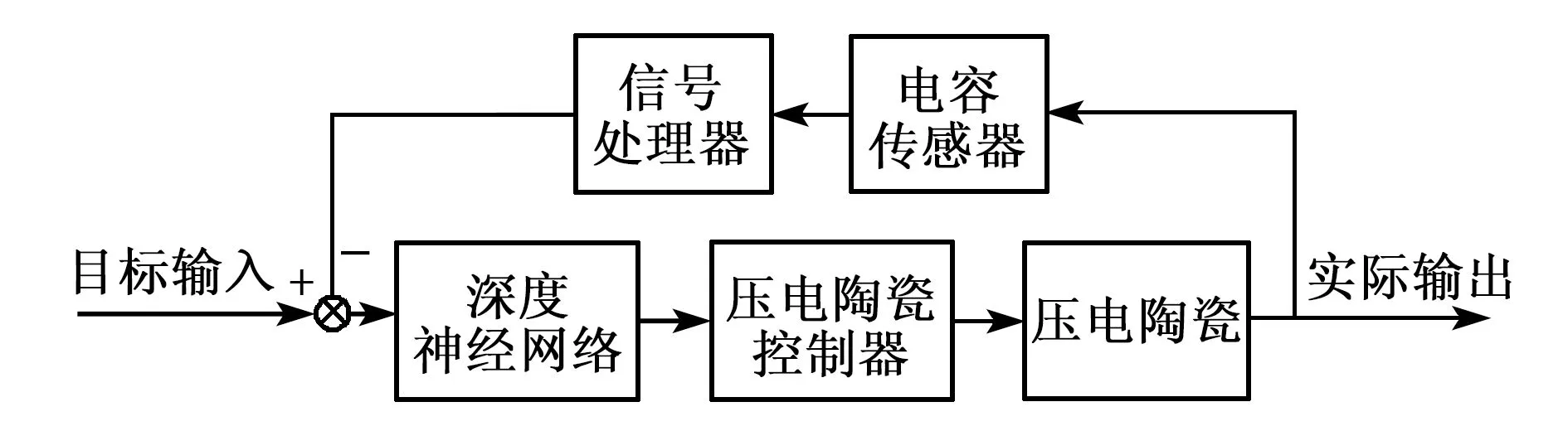
图5 深度神经网络前馈控制示意图

2 深度神经网络

一个或若干个神经元组成一层神经网络，将若干层神经网络依次连接，得到一个深度神经网络(DNN)[12-13]，如图6所示。

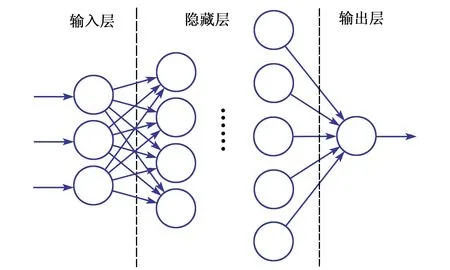
图6 深度神经网络结构

深度神经网络层与层之间是全连接的，即第i层的任意一个神经元与第i+1层的任意一个神经元相连，其计算关系如图7所示。一个线性关系z=

∑(wixi)+b加上一个激活函数σ(z)，激活函数能够增加神经网络的非线性表达能力，也对应了压电陶瓷的迟滞非线性。

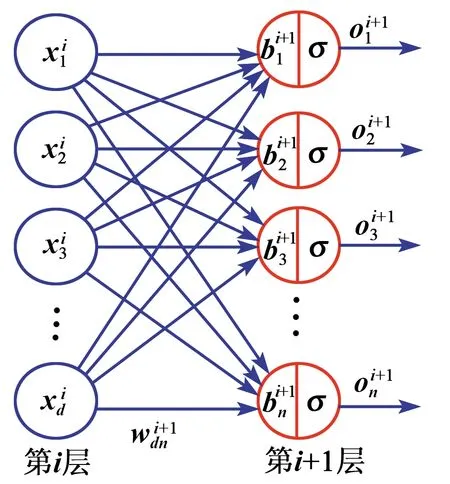
图7 深度神经网络计算关系

假设第i层具有n个神经元，第i+1层具有d个神经元，第i+1层中每个神经元包含一个偏置量，从第i层到第i+1层的关系为

(5)

将式(5)简化可得：

(6)

式中o为O矩阵中的元素。可将式(6)写成矩阵形式：

O=σ(WX+b)

(7)

式中：O∈d×1为第i+1层的输出，为空间，d×1为维度；W∈d×n为第i层到i+1层的隐藏层权重；X∈n×1为第i层的输出；b∈d×1为第i+1层的偏置。

为了构建更通用的多层网络结构，可以继续堆叠这样的隐藏层，如O(1)=σ1(W(1)X+b(1))和O(2)=σ2(W(2)O(1)+b(2))，一层叠一层，从而产生更有表达能力的模型[14]。

深度神经网络不仅有强大的非线性拟合能力、特征提取能力和容错能力，而且在面对海量、高维度的数据时，表现优于机器学习[10]。

2.1 模型设计

设计的深度神经网络层数为9层，输入层包含3维(当前实际位移、上一次输入电压和上一次位移)，输出层1维(压电陶瓷输入电压)。训练数据集由第1节得到的3种迟滞回线的数据拼接而成，共有5 860组数据。表1为全连接层神经元个数。

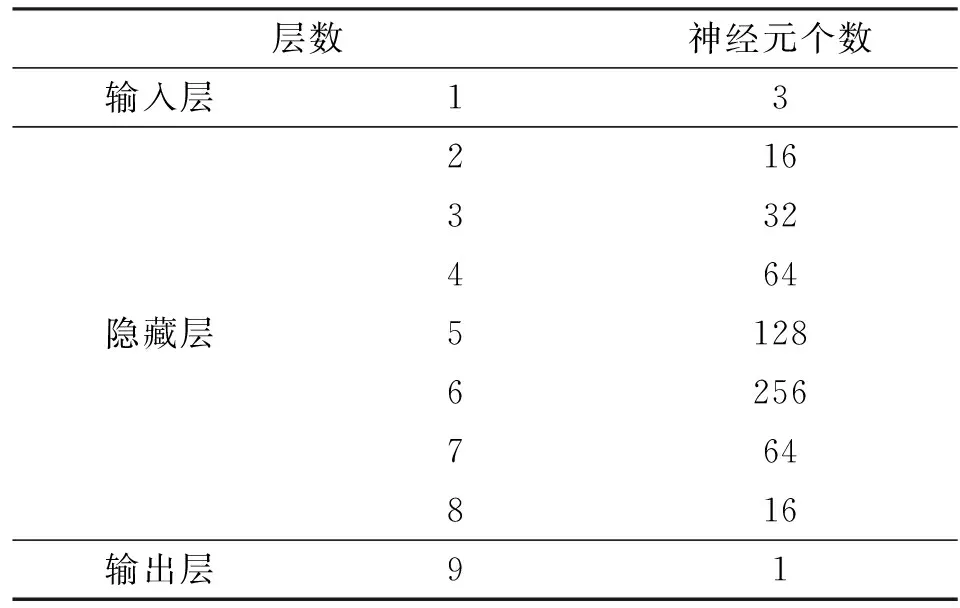
表1 全连接层神经元个数

2.2 模型训练

2.2.1 训练过程

神经网络训练过程(见图8)：

1) 初始化权重值参数，将每一组训练数据中的xt、Vt-1和xt-1作为神经网络的输入，通过前向传播算法逐层计算，得到输入电压预测值后，与Vt进行对比，计算损失值。

2) 在反向传播算法中，根据选择的优化器更新神经网络权重参数。经过一轮一轮训练，得到最小损失值，此时神经网络模型为f′函数，见式(4)。经过100 000轮训练后，得到了符合精度要求的模型，损失值如表2所示。

图8 神经网络训练过程流程图

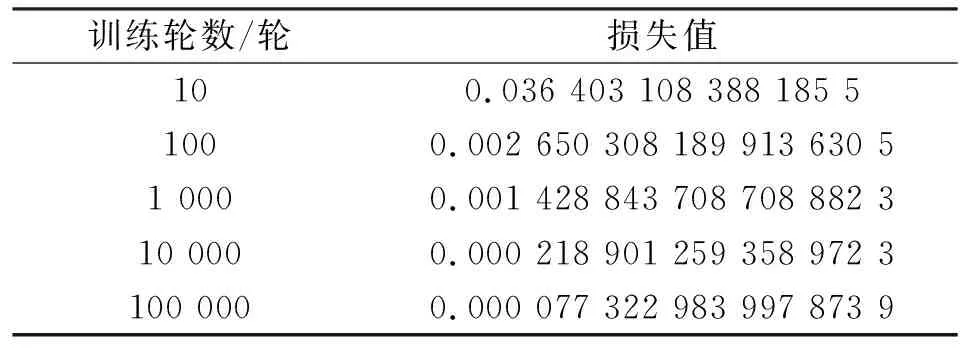
表2 损失值表

2.2.2 损失函数

(8)

式中N为样本大小。

2.2.3 优化器与学习速率

在反向传播算法中，选用目前最常用Adam优化器作为参数更新方式，它能自适应地调节学习速率αt，使训练能更快地收敛[15]。参数更新式为

(9)

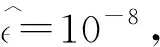
3 实验测试

在图1实验平台上对模型有效性进行了验证。在PC端设置目标位置分别以频率为10 Hz的三角波、正弦信号、增幅正弦信号、减幅正弦信号变化，经神经网络模型前馈补偿后到控制器产生压电陶瓷输入电压，测试微位移台实际位置，结果如图9～12所示。当设置为三角波信号时，目标位置与实际位置成良好线性关系，最大误差值-0.088 μm，出现在初始点0处，稳态误差基本在±0.02 μm内。当目标位置设置为正弦信号、减幅正弦信号和增幅正弦信号时，最大误差都有不同程度的增加，分别为-0.67 μm，-0.66 μm和-0.27 μm，但仍出现在初始点处，系统稳态误差控制在±0.1 μm内。由图11、12可知，随着振幅增大，误差也相应增大。

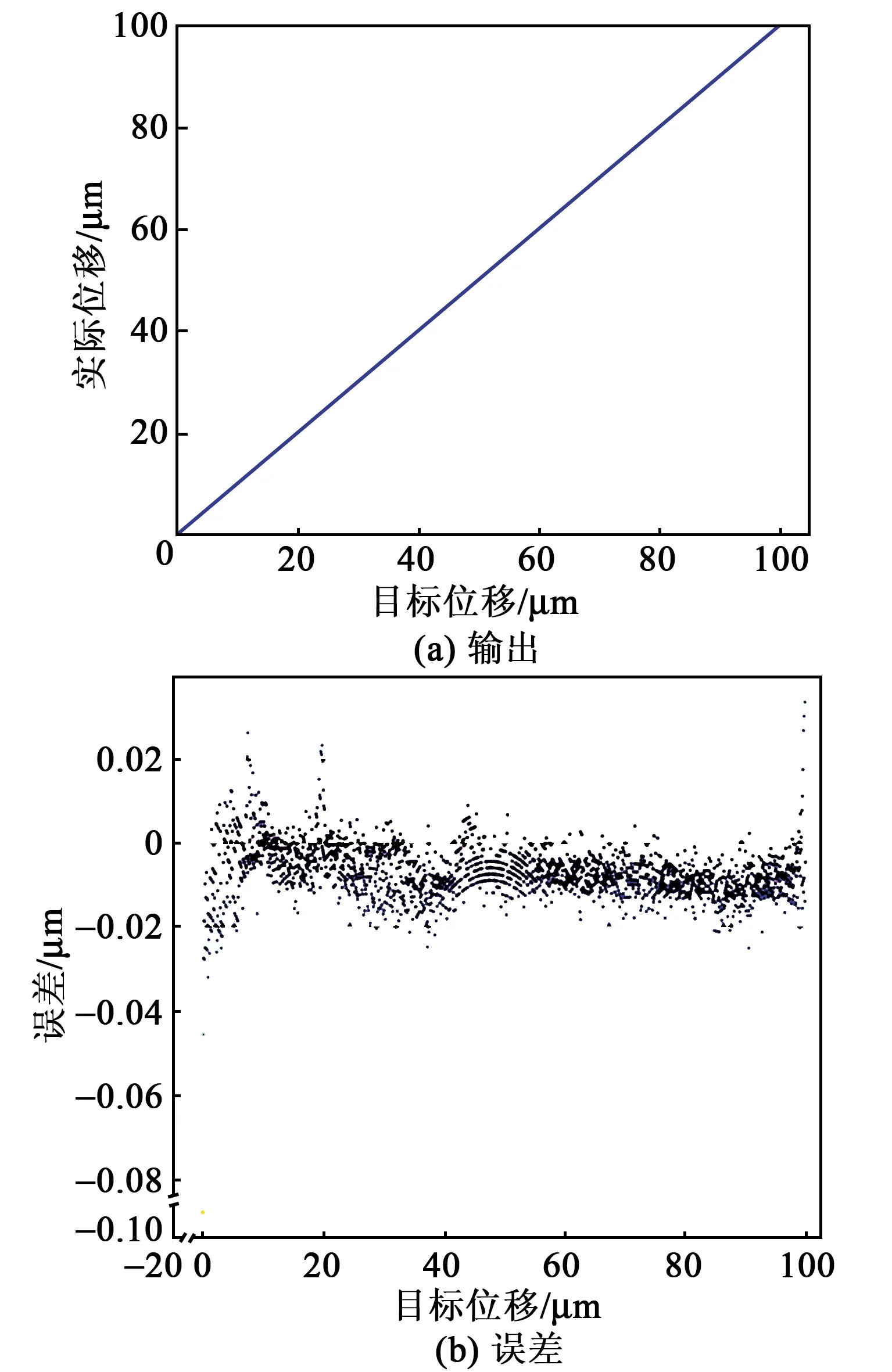
图9 步进运动控制效果图

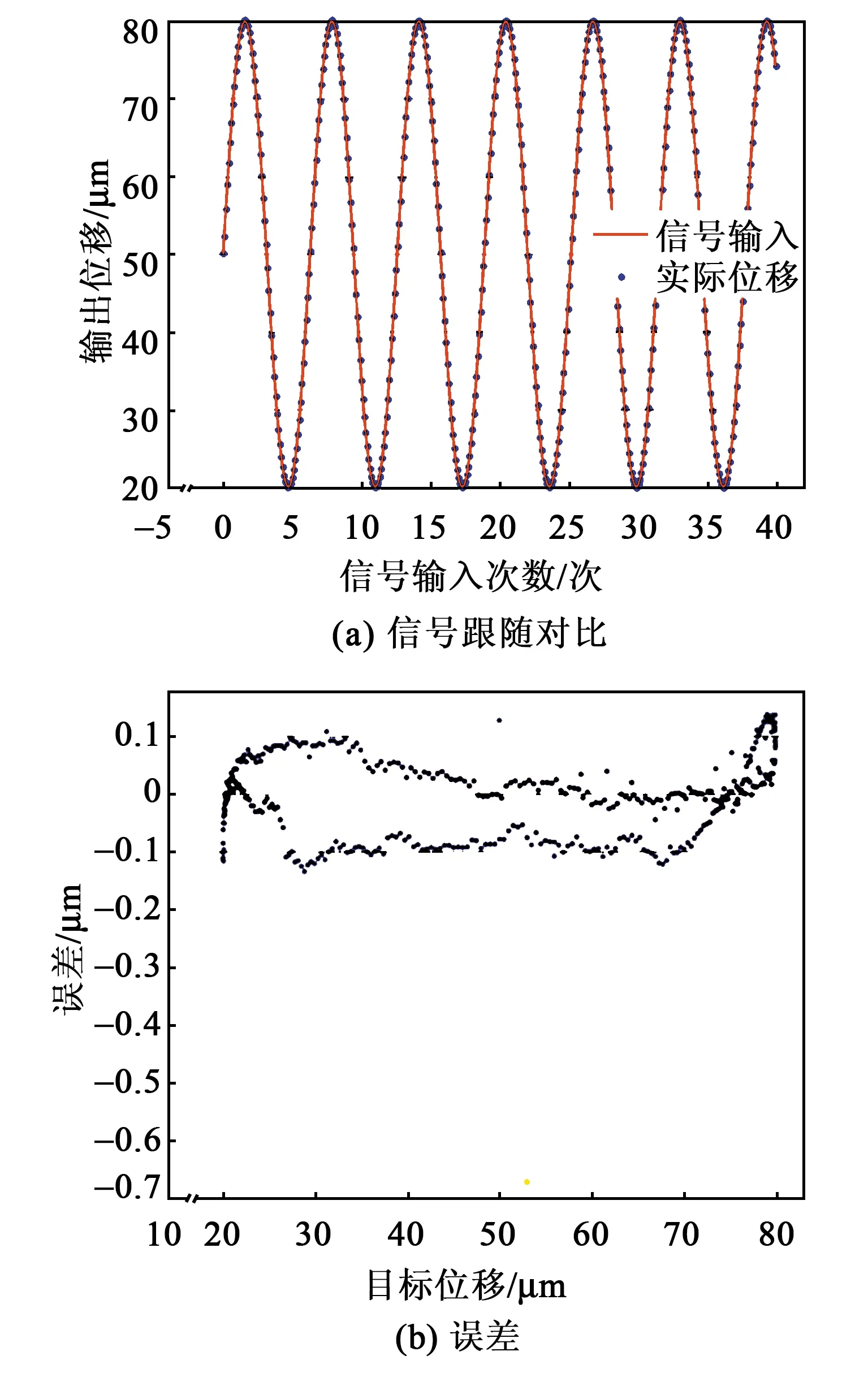
图10 跟随正弦输入信号运动控制效果图

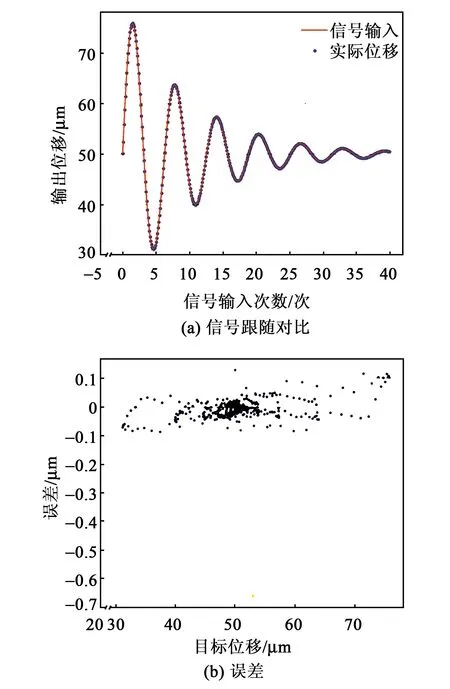
图11 跟随减幅正弦输入信号运动控制效果图

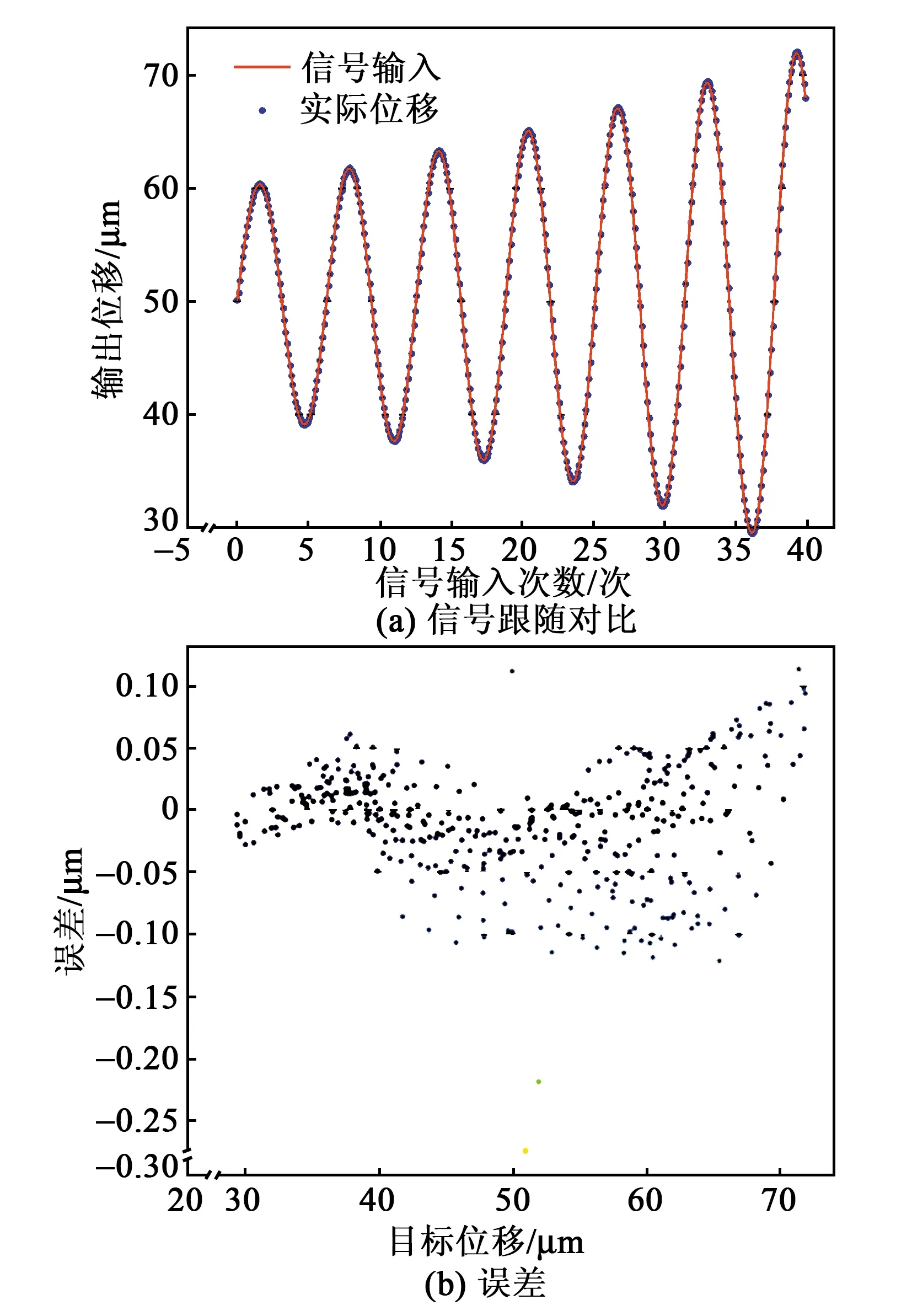
图12 跟随增幅正弦输入信号运动控制效果图

当目标位置依次按20 Hz、50 Hz和100 Hz三角波变化时，测试了微位移台的实际位置，验证了神经网络模型的频率泛化能力。

为了获得较好的对比效果，应用均方根误差(ERMSE)反映误差分布的离散程度，其表达式为

(10)

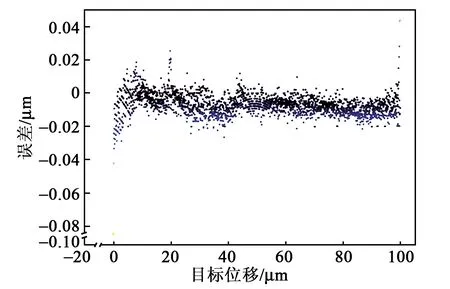
图13 20 Hz输入频率控制效果图

图13～15分别为20 Hz、50 Hz和100 Hz时的控制效果图。表3为不同输入频率下的控制效果对比。

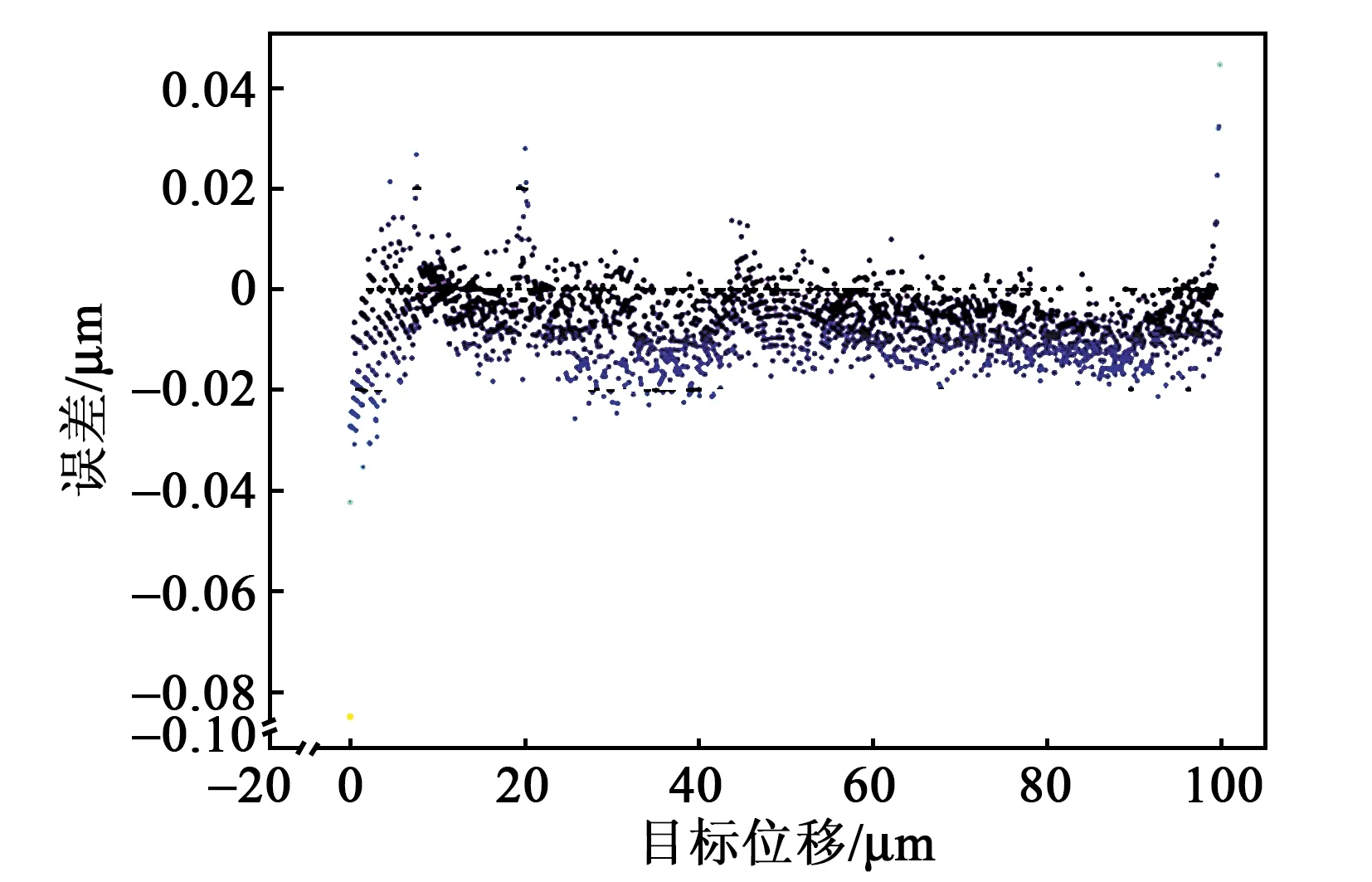
图14 50 Hz输入频率控制效果图

图15 100 Hz输入频率控制效果图

表3 不同输入频率下控制效果对比

由图13～15可知 ，随着目标位置输入频率的升高，最大误差和均方根误差呈现增大的趋势，说明提高目标位置输入频率会增加压电陶瓷的迟滞非线性。当输入频率为100 Hz时，最大误差为-0.097 μm，仍在可接受的工程应用范围内，表明构建的深度神经网络模型在10～100 Hz具有良好的频率泛化能力，整体上能以较高的精度拟合压电陶瓷迟滞非线性特性。

4 结束语

本文基于PyTorch深度学习框架构建了一个包含9层网络结构和ReLU激活函数的深度神经网络模型，给出了模型的设计原理和训练过程，并将训练得到的模型应用于压电陶瓷微位移台的前馈补偿。测试结果表明，在10 Hz的输入信号下，位移最大误差在-0.08 ～-0.67 μm，系统稳态误差为20～100 nm。随着频率的提高，误差增加，100 Hz时最大误差为-0.097 μm，仍在可接受的工程应用范围。结果说明，本文构建的深度神经网络能够准确地描述压电陶瓷的动态迟滞非线性，具有较好的频率泛化能力，可以应用在同步辐射光束线单色器第二晶体俯仰角前馈补偿中，为优化光束线实时智能调束系统提供参考和帮助。

本文应用的深度神经网络模型的设计方法不仅适用于压电陶瓷驱动器前馈控制，对其他非线性系统建模也具有一定参考价值。用于深度神经网络建模的PyTorch框架，易于编程、参数调整和模型的实现只要对系统测量得到足够多、覆盖全的工作状态作为构建模型的训练数据集，然后构建合理的神经网络，经过足够多的训练，最后就能得到与系统对应的深度神经网络模型。