一种圆盘压电滤波器的研究
2022-03-16王宏伟于肇贤
荣 畋,王宏伟,于肇贤
(北京信息科技大学 理学院,北京 100192)
0 引言
随着世界各国军事、科研及民用领域信息通讯需求的不断增加,通信质量成为了一个亟待提高的问题。滤波器作为信号处理系统中至关重要的组件,其性能的优劣直接影响着复杂信号中噪声[1]的滤除及信号的提取。目前各国研究学者在传统滤波器基础上进行优化改进,并获得了性能更优异的各类滤波器。杨坪坪等[2]提出了一种用于CT成像的改进高斯滤波器,通过提升系统抗噪声性能来提高传输图像的质量;崔文翔等[3]采用保偏光纤制作了一种激光滤波器,实现了多波长激光传输;曹珂[4]设计的椭圆函数滤波器可以实现良好的带外抑制效果。但是以上各类滤波器针对的是各自超高频领域内的应用,且结构复杂,不适用于军事、科研及民用领域的中高频信息通讯。随着科学技术的发展和人们生活水平的提高,电子产品在具有优美外观的同时还必须具有良好的散热特性及一定的抗干扰能力,而具有频率选择性的压电陶瓷滤波器具有成本低,抗电磁干扰能力强及散热性能良好的特性,将逐渐取代晶体滤波器和传统滤波器[5]。目前常见的压电滤波器主要有:
1) 王兴超等[5-7]研制的具有单一滤波特性的高频压电陶瓷滤波器,主要以铌锌锆钛酸铅压电陶瓷材料的厚度振动实现滤波,但滤波功能单一,不能实现多频选择滤波的功能。
2) 山本隆等[7]研制的多层压电陶瓷块滤波器,通过连接串、并联谐振器以形成梯形回路实现滤波功能,但其结构较复杂,压电陶瓷块之间无法准确产生预定的接触压力,使得滤出频率发生偏移。
3) HEDIYEH F等[8-9]研制的压电薄膜滤波器实现了双极滤波功能,但滤波器工作频率较高,不适用于音频信号滤波。
此外相对于其他压电材料,温度稳定性较高的PZT4压电材料具有较低的机械损耗、较大的机电耦合系数和压电常数。因此,采用PZT4材料,制作工艺简单,具有选择性滤波功能,未附加接触应力要求的圆盘状压电滤波器将具有更优异的性能和应用前景。
1 圆盘压电滤波器的结构
本文研制的压电滤波器由信号输入端、无电极隔离槽及信号输出端3部分组成,如图1所示。

图1 圆盘压电滤波器
由图1可知,信号输入端、输出端及无电极隔离槽厚度相同,在径向方向上相连,三者仅在上表面电极进行分割,下表面电极作为整体公共负电极不进行分割。当信号施加在信号输入端时,会引起输入端产生机械振动,振动沿径向传导至无电极隔离槽和信号输出端,引起输出端产生对应的振动,根据正压电效应,输出端会输出对应的信号。由于压电陶瓷具有频率选择性,在不同频率信号的驱动下具有不同的振动模态,其输出端也会产生对应频率的信号,故而具有滤波的功能。滤波器的实际体积参数对其振动模态和实际应用具有很大影响,因此,本文将通过理论计算和ANSYS有限元仿真确定滤波器的尺寸参数。
2 圆盘压电滤波器理论分析
压电滤波器输入端在不同频率的作用下具有不同的振动模态,因此对其每种模态进行分析较复杂。为确定压电滤波器的尺寸参数和振动频率,可先选择厚度振动特性进行分析,并在此基础上进行仿真和实验,以确定其滤波特性。
求解压电滤波器的谐振频率时,可对压电滤波器输入端进行理论分析,得到相关参数后可对压电滤波器谐振频率进行推论。设压电滤波器输入端的厚度为tfilter,横截面面积为Sfilter。滤波器的厚度可与波长λ相比,横向尺寸(圆盘的直径)比厚度大,则其压电方程可简化[10]为
(1)

电路状态方程为
I=jωSfilterD3=jωC0V-n(v1+v2)
(2)
式中:I为流过圆盘的电流矢量;v1、v2分别为输出端在厚度方向上、下端面处的振动速度矢量;V为上下端面施加的电压;ω为角频率;C0、n分别为截止电容和机电转换系数。D3,C0,n的表达式分别为
(3)
(4)

(5)
式中X1、X2为上、下表面厚度振动位移矢量。根据输入端振动的理想模型,可得压电圆盘的运动方程:

(6)
式中:ρ为PZT4型压电陶瓷密度;X为厚度方向的位移变量;t为时间;z为厚度方向。引入如下参数:
(7)
(8)
式中:v为纵波声速矢量;k为波数。则对于简谐激励,可得输出端振动位移方程:

(9)
式(1)中应力表达式与Sfilter相乘即可得输入端内部力的分布。输入端上下表面的力应与外力平衡,则有:
(10)
式中F11、F21为作用于厚度方向上、下端面的外力矢量。将式(3)、(9)代入式(10)可得厚度机械振动方程:
(11)
根据式(2)、(11)可得输入端等效电路如图2所示。

图2 输入端等效电路
当输入端在空气中自由振动时,其上下端面未施加外力,此时F11=F21=0,由此可将图2电路简化为图3所示的机电等效电路图。

图3 空气中自由振动机电等效电路图
为进一步计算输入端的阻抗,可将自由振动机电等效图化简,如图4所示。
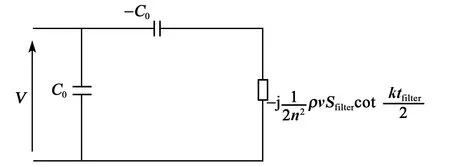
图4 空气中自由振动等效电路简化图
图4中,经过机械阻抗的运算可得输入端的等效电阻抗:
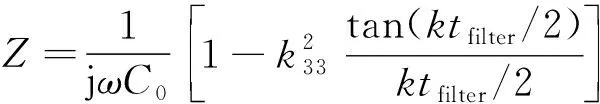
(12)


(13)
以实际工艺为前提,取信号输出端半径4 mm,信号输入端内半径7 mm,外半径25.5 mm,tfilter=6.9 mm,则可得滤波器厚度振动频率为297 kHz。事实上,输入端带动无电极隔离槽和输出端进行振动,相当于输入端携带质量负载,故压电滤波器整体厚度振动频率应略低于输入端的厚度振动频率。
实验前期,仿真分析了压电陶瓷横截面积对厚度振动谐振频率的影响[9],表明随着横截面积的增大,厚度振动的谐振频率略微降低。因此,综合考虑实际工艺和用途,本文设计生产了一款信号输出端半径4 mm、输入端内半径7 mm、外半径25.5 mm、tfilter=6.9 mm的圆盘压电滤波器。
3 圆盘压电滤波器的仿真和制作
为进一步观察压电滤波器的振动模态,验证理论模型的计算结果,使用ANSYS有限元软件对压电滤波器进行仿真分析。
3.1 圆盘压电滤波器的仿真
在ANSYS有限元仿真软件中,将滤波器分解为信号输入端、无电极隔离槽、信号输出端3部分建模后,使用布尔操作中的粘贴功能,将3部分进行连接。赋予圆盘solid5单元类型并设置网格密度,划分网格,施加激励条件后,计算观察圆盘的振动频率,其导纳曲线如图5所示。

图5 压电滤波器导纳图
由图5可知,压电滤波器峰值约为294 kHz,观察该频率下圆盘的振动模态,如图6所示。
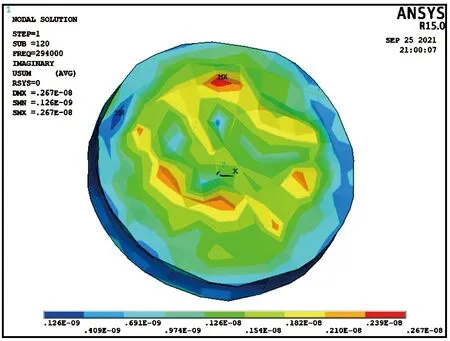
图6 294 kHz振动模态
由图6可知,圆盘做厚度振动,即本文设计的圆盘压电滤波器厚度振动谐振频率为294 kHz,图中振动模态出现略微不对称性是因为网格划分计算分析与实际振动仍有略微差别。这一仿真结果与理论计算式相近,因此,物理模型计算结果正确,所设计尺寸可用于圆盘压电滤波器的制作。
3.2 圆盘压电滤波器的制作
以理论计算结果和仿真数据为依据,制作圆盘压电滤波器。采用环形切割压电陶瓷块—打磨无电极隔离槽—涂覆补偿银电极的方式,制作半径为25.5 mm的圆盘压电滤波器。
上表面电极由输入、输出电极和隔离槽构成。输出电极是与压电材料同轴心、半径为4 mm的圆盘,其外围是内半径4 mm、外半径7 mm的隔离槽,将输入电极和输出电极隔开。输入电极是与压电材料同轴心,内半径7 mm、外半径25.5 mm的圆环。作为公共负电极的下表面电极是一个与压电材料同轴心的圆盘。涂覆补偿银电极后,引出导线,最终制作成圆盘压电滤波器如图7所示。

图7 圆盘压电滤波器
4 圆盘压电滤波器的测试
在不同驱动频率的作用下,压电滤波器具有不同的振动模态,因此,其输出频率也会发生变化。为观察其输入、输出信号频率的关系,在自主设计的实验平台上进行测试。在信号输入端输入幅度相同、频率不同的正弦波信号,使用示波器观察其输出端信号,可得其输出端信号频率随输入端信号频率变化如图8所示。
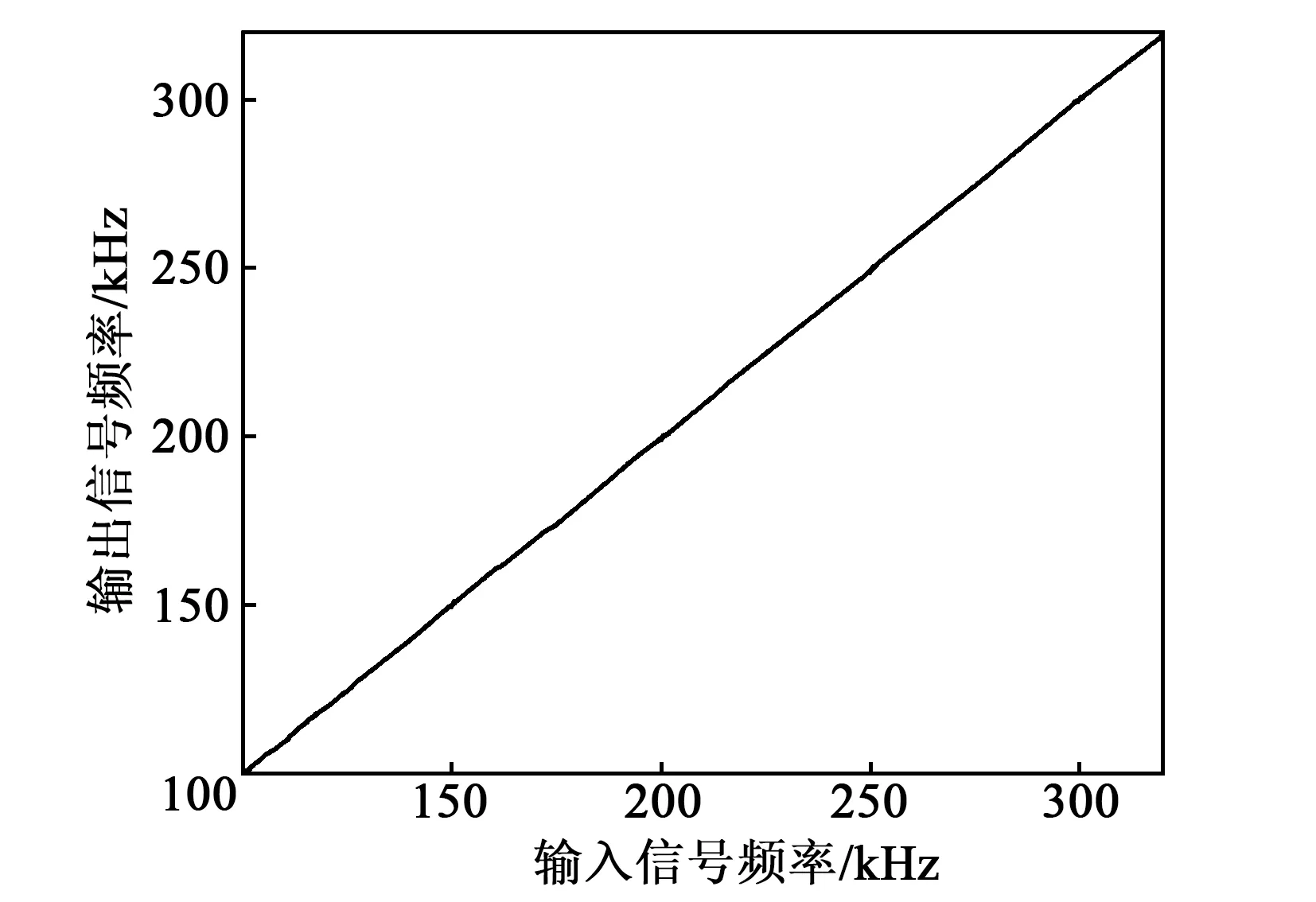
图8 输出频率变化曲线
由图8可知,圆盘滤波器的输出信号频率与输入信号频率近似相等,当输入信号以一定的频率施加在信号输入端,输入端会带动信号输出端振动,进而输出与原信号相同频率的输出信号。随机施加不同频率的信号,使用示波器观察其输出端信号频率,其结果如图9所示。
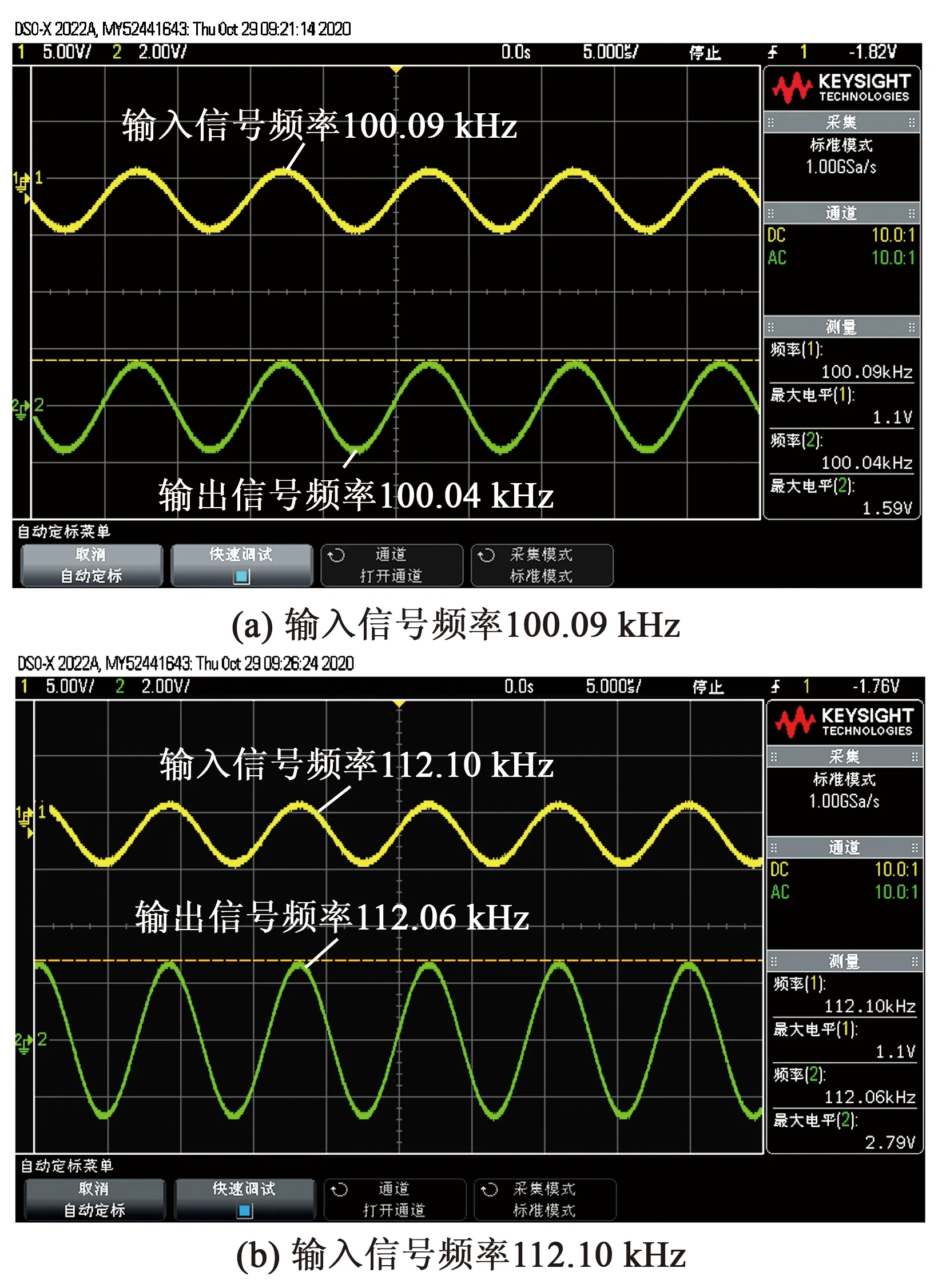

图9 输入输出信号频率测量
由图9可知,根据测试结果,圆盘压电滤波器输出端信号频率与输入端信号频率保持一致,表明本文所研制的圆盘压电滤波器具有良好的滤波特性。
5 结束语
本文通过理论上建立物理模型和ANSYS有限元软件仿真确定了圆盘压电滤波器的尺寸参数。采用环形切割压电陶瓷块—打磨无电极隔离槽—涂覆补偿银电极的方式制作了厚度谐振频率约297 kHz的圆盘压电滤波器,该滤波器在不同频率处具有不同的振动模态,其输出端信号的频率也会随之发生变化。
对于不同频率的输入信号,可以通过在压电滤波器输入端连接频率调制电路,将输入信号频率调制到所需频率处,滤波器输出信号后进行解调,还原出原频率下的信号,从而实现最佳的滤波性能。
所研制的圆盘压电滤波器可应用于需求小体积高滤波性能的电子产品,如笔记本电脑中,也可应用于具有较强电磁干扰的场合。其良好的滤波特性,对之后的研究也具有较大的借鉴意义。
