摩擦参数对压电执行器振动特性的影响

王 鹏, 孙志礼, 吴 楠, 骆海涛

(1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819; 2. 曼尼托巴大学 工程系, 加拿大 温尼伯 R3T2N2; 3. 中国科学院 沈阳自动化研究所, 辽宁 沈阳 110016)

大多数具有滑动表面的机械系统,如制动系统、离合器、位置控制系统等,都会发生摩擦诱发振动.近年来,摩擦作用下的结构振动特性,包括动静摩擦的转换[1-2]、系统稳定性分析[3]、摩擦下的能量采集[4-6]和主动振动控制[7]受到了研究者的关注.

执行器是近年来在工程上广泛应用的一种机构,根据驱动原理,精密执行器的类型包括电致伸缩、磁致伸缩、人工肌肉执行器、形状记忆合金、光致伸缩和机械力化学执行器[8].执行器有以下几个优点[9]:可以产生非常精细的位移,通常在纳米范围内;具有快速的频率响应,能够以非常高的频率工作;具有较大的刚度;压电驱动在接合时消耗的功率非常小.基于以上优点,执行器的主要应用之一是和压电材料一起用作主动振动控制.其中摩擦力作用下压电执行器的主动控制具有重要意义[7,10-11].振动特性分析是压电应用的前提,摩擦工况下的静态和振动控制都需要了解压电摩擦诱发振动的响应,从而提供所需要的振动控制信号.摩擦力是一种实时变化的动态力,所以很难得到摩擦力作用下的结构振动响应的解析解.据作者所知,还没有对摩擦力作用下的压电执行器的振动特性和参数分析的研究.

鉴于以上分析,本文采用迭代法计算和分析压电执行器在摩擦力作用下的振动特性.研究了参数变化对摩擦力和振动特性的影响.引入弹性双线性和三线性,研究参数变化对于摩擦力作用下的双线性压电执行器[12-15]的振动特性和摩擦力的影响并比较了单线性、双线性和三线性[16]压电执行器的摩擦力和振动特性.

1 数学建模

摩擦力作用下的压电执行器模型如图1所示.左右两边的柔性铰链刚度为kq(左右相等)并和中间的压电堆相连,kq=E/lA,E为柔性铰链的弹性模量,l为图中柔性铰链的长度,A为柔性铰链的横截面积.柔性铰链和3方向的角度为α(α′),kp3为压电堆的3方向刚度.压电堆和下面的压电堆底座相连,压电堆底座可以沿着1方向自由滑动.压电堆底座、压电堆和柔性铰链的等效质量为m.上面的刚性板和压电堆接触并以速度v向右(正方向)匀速运动,正压力FN作用在板上.假设振动过程中压电堆只有纵向变形,柔性铰链的变形会造成压电堆的横向位移和纵向变形且横向位移和α(α′)的变化很小.那么压电执行器的等效刚度为

图1 摩擦力作用下的压电执行器模型Fig.1 Piezoelectric actuator model under friction force(a)—主视图； (b)—俯视图.

k=k1+k2.

(1)

式中:k1和k2为压电堆左右两边柔性铰链的等效刚度,k1=8kq(sinα)2(kp3)2/(2kp3+kq-kq(sinα)2)2,k2=8kq(sinα′)2(kp3)2/(2kp3+kq-kq(sinα′)2)2.

压电执行器在摩擦力作用下的振动方程为

(2)

式中:c为阻尼系数,c=2mωξ,ξ是阻尼比,ω是固有频率;f(t)为板作用在压电堆上的摩擦力;x(t)为压电堆在摩擦力作用下的振动响应.

本文采用迭代法来计算摩擦力作用下压电堆的振动响应.迭代法的前提是假设时间为0 s时系统的初始状态是已知的.迭代步长为Δt=tn+1-tn, 1≤n<∞,下标n表示迭代步数.在时间t1=0 s时的初始条件为

(3)

式中x1(t1)是压电堆的初始位移.

时间为t1-t2时,压电堆和刚性板之间处于黏着状态,压电堆随着板一起向右匀速运动.压电堆时间为t1-t2时的振动响应为

x1(t)=v·t,t1≤t≤t2.

(4)

作用在压电堆上的黏着摩擦力为

f1(t)=x1(t)·k,t1≤t≤t2.

(5)

式中摩擦力和两个柔性铰链弹力合力的大小相等、方向相反.

时间为t2-t3时,如果柔性铰链的弹力满足|x1(t2)·k|≤FN·μS,μS是静摩擦系数.压电堆和板之间仍然处于黏着状态,压电堆的振动响应为

x2(t)=v·(t-t2)+x1(t2),t2≤t≤t3.

(6)

作用在压电堆上的黏着摩擦力为

f2(t)=x2(t)·k,t2≤t≤t3.

(7)

如果柔性铰链的弹力满足|x1(t2)·k|>FN·μS,压电堆和板之间为滑动状态,假设短时间内压电堆的速度没有变化,作用在压电堆上的滑动摩擦力为[17]

(8)

(9)

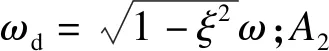
e-ξωt2(A2cosωdt2+B2sinωdt2)=x1(t2) ,

(10)

(11)

通过以上两式可以得到A2和B2:

(12)

(13)

在时间为tn-tn+1时,压电堆的振动响应和所受摩擦力计算如下:

xn(t)=v(t-tn)+xn-1(tn),tn≤t≤tn+1.

(14)

作用在压电堆上的黏着摩擦力为

fn(t)=xn(t)·k,tn≤t≤tn+1.

(15)

tn≤t≤tn+1.

(16)

压电堆的振动响应为

xn(t)=xfreen(t)+xforcen(t)=

e-ξωt[(Ancosωdt+Bnsinωdt)+

τ))dτ],tn≤t≤tn+1.

(17)

(18)

(19)

压电堆和板之间为黏着时,如果|k·xn-1(tn)|≤FN·μS,压电堆和板之间处于黏着状态.压电堆的振动响应和所受黏着摩擦力可由式(14)和(15)计算.

如果|k·xn-1(tn)|>FN·μS,压电堆和板之间处于滑动状态.作用在压电堆上的滑动摩擦力为

(20)

压电堆的振动响应为

xn(t)=xfreen(t)+xforcen(t)=

e-ξωt[(Ancosωdt+Bnsinωdt)+

τ))dτ],tn≤t≤tn+1.

(21)

式中An和Bn可以由式(18)和(19)求解.

多线性指的是菱形结构(柔性铰链)的等效结构刚度在柔性铰链的变形达到一定数值时发生改变.文中使用了多线性模型简化和模拟这种刚度的连续变化,一次改变就是双线性,发生两次改变就是三线性,x′和x″是双线性和三线性发生变化时对应的菱形结构的变形量.在本文中认为α在振动过程中只有在角度变化量达到一定范围时才会发生变化，进而使等效刚度发生变化,范围由柔性铰链的材料属性决定,本文只研究等效刚度多线性下的压电执行器的振动响应和参数分析,不讨论具体的材料属性.双线性压电执行器是指当压电堆的位移x(t)大于x′时等效刚度变为k′.当x(t)>x′时,压电执行器在摩擦力作用下的振动方程为

(22)

同理,三线性压电执行器在压电堆的位移大于x′ 时等效刚度变为k′,位移大于x″ 时等效刚度变为k″.当x(t)>x″ 时,压电执行器在摩擦力作用下的振动方程为

k″(x(t)-x″)=f(t) .

(23)

双线性和三线性压电执行器对应的是不同的系统,它们在摩擦力作用下的振动响应求解过程与单线性压电执行器相同,本文所提的迭代方法可以用来求解摩擦力作用下多线性压电执行器的振动响应.

2 参数分析

研究不同的参数对已知压电执行器(k和m不变)振动特性的影响,对其中一项参数进行分析时其他参数保持不变.时间长度为0.05 s,时间间隔为10-6s,ξ=0.001.FN和v对摩擦力的影响如图2所示,图3显示了FN和v对压电堆振动特性的影响.FN的变化范围是500～900 N,v的变化范围是0.01～0.05 m/s,k=0.8×106N/m,μS=0.5,μD=0.3,C=6,m=2 kg.

从图2可以看出，正压力FN越大,最大静摩擦力越大.板的运动速度v越大,板和压电堆之间从黏着转到滑动摩擦的时间越短,滑动摩擦力的最小值越小.

图2 FN,v对摩擦力的影响Fig.2 Influence of FN,v on friction force(a)—v=0.03 m/s； (b)—FN=700 N.

从图3中可以看出,压电堆的振幅随着正压力FN和板运动速度v的增加而增大.从具体数据可知,在所研究的参数范围内,当v=0.01 m/s时振幅随着FN的增加幅度是最大的,当FN增加为原来的1.8倍时振幅增加到1.84倍.当FN=500 N 时振幅随着v的增加幅度是最大的,速度增加为原来的5倍时振幅增加到原来的4.17倍.其中位移和速度曲线和文献[17]中的试验结果(文献中图6)相比虽然参数不同导致数值上有所差异,但是位移和速度都具有相同的趋势,可以验证本文数学模型的正确性.μS,μD和C对压电堆振幅的影响如表1所示.μS,μD和C对摩擦力的影响如图4所示,其中FN=700 N,v=0.03 m/s,k=0.8×106N/m,m=2 kg.

图3 FN,v对振动特性(振幅)的影响Fig.3 Influence of FN,v on vibration characteristics(amplitude)

从表1可知在所研究的参数范围内,压电堆振幅随着μS的增加而变大,μS增加为原来的2.3倍时振幅增加到9.77倍.压电堆振幅随着μD的增加而减少,μD增加为原来的5倍时振幅减少到0.23倍,压电堆振幅随着C的增加而变大,C增加为原来的5倍时振幅增加到2.3倍.

表1 μS,μD和C对振幅的影响Table 1 Influence of μS,μD and C on amplitude

从图4可以看出μS主要影响最大静摩擦力的大小,μS越大,最大静摩擦力越大.μD主要影响滑动摩擦力的大小,μD越大,滑动摩擦力越大.

图4 μS,μD和C对于摩擦力的影响Fig.4 Influence of μS,μD and C on friction force(a)—μS对摩擦力的影响(μD=0.5,C=6)； (b)—μD对摩擦力的影响(μD=0.6,C=6)； (c)—C对摩擦力的影响(μS=0.5,μD=0.3).

C主要影响黏着和滑动摩擦状态之间的转换速度,C越大,摩擦力从最大黏着摩擦力转到相同数值的滑动摩擦力的时间越短,从滑动转到黏着状态对应的时间点越小.

阻尼比对振幅、频率和摩擦力的影响如图5所示.其中最小黏着摩擦力是指压电堆和板之间第一次从滑动转为黏着状态时作用在压电堆上的黏着摩擦力的最小值.阻尼比的取值范围为0.000 1 ～0.01,k=0.8×106N/m,μS=0.5,μD=0.3,C=6,m=2 kg,FN=700 N,v=0.03 m/s.

从图5可以看出,在所研究的参数范围内,随着阻尼比的增加,压电堆的振幅逐渐减小,最小黏着摩擦力和最小滑动摩擦力随着阻尼比的增加而变大.

图5 阻尼比对振幅和摩擦力的影响Fig.5 Influence of damping ratio on amplitude and friction force

经过计算,在所研究的参数中μS和μD对频率的影响程度最大,结果如图6所示.其他参数k=0.8×106N/m,C=6,m=2 kg,FN=700 N,v=0.03 m/s.

从图6可以看出在所研究的参数范围内,频率随着μD的增加而增加,随着μS的增加而减少.

图6 μS和μD和对于工作基频的影响Fig.6 Influence of μS and μD on frequency

在之前研究的基础上,引入弹性双线性,即当压电堆的位移达到一定值(阈值)时,压电执行器的等效刚度k发生变化.线性压电执行器在参数为FN=700 N,μS=0.5,μD=0.3,C=6,v=0.03 m/s,k=0.8×106N/m,m=2 kg时压电堆距离平衡位置的最大位移为4.8×10-4m.双线性压电执行器的阈值由线性压电执行器位移(4.8×10-4)的20%变到80%,等效刚度k由0.8×106N/m跳跃到1.4×106N/m.经过计算阈值变化对最小黏着摩擦力的影响比较大,结果如图7所示,其中最小黏着摩擦力是指压电堆和板之间第一次从滑动转为黏着状态时作用在压电堆上的黏着摩擦力的最小值,对应的时间点即为转换时间.阈值对压电堆振幅的影响如图8所示.

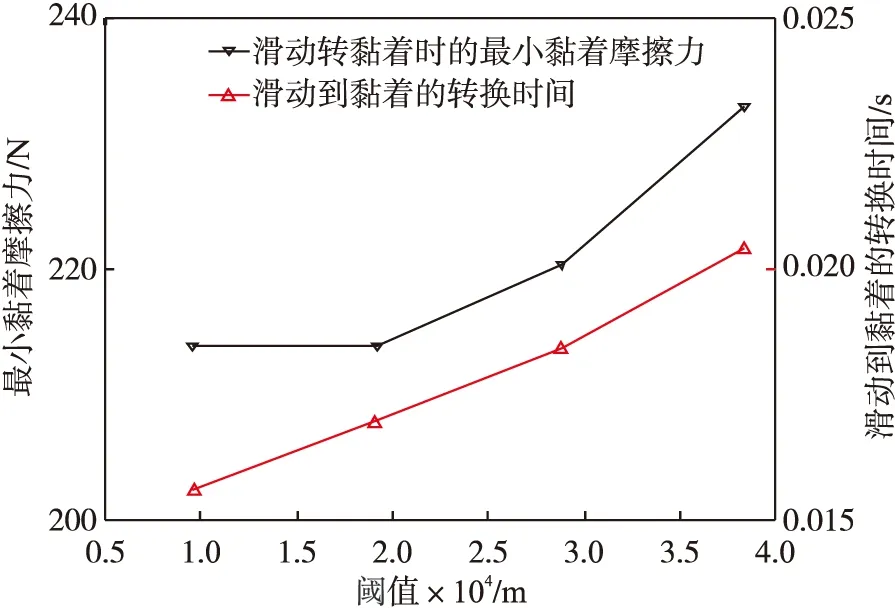
图7 阈值对滑动转黏着后的最小黏着摩擦力和转换时间的影响Fig.7 Influence of threshold on minimum stick friction force and transformation time after sliding to stick

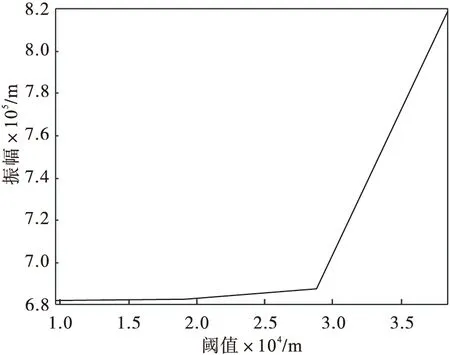
图8 阈值对振幅的影响Fig.8 Influence of threshold on amplitude

在阈值为4.8×10-4×50%m时,k的上限由0.8×106N/m 跳跃到 1.2×106N/m, 多线性等效刚度k的上限对最小滑动摩擦力影响比较大,结果如图9所示.

从图7和8可知当双线性发生时,压电堆的振幅、最小黏着摩擦力和对应的转换时间随着阈值的增加而变大.从图9可知压电堆的振幅随着等效刚度的增大而变大,最小滑动摩擦力随着阈值的增加而减小.

图9 等效刚度的上限对振幅和最小滑动摩擦力的影响Fig.9 Influence of upper limit of equivalent stiffness on amplitude and minimum sliding friction force

同理,在双线性的基础上引入弹性三线性,其中三线性压电执行器在阈值为4.8×10-4×30 %m时,k的上限由0.8×106N/m跳跃到1.0×106N/m.在阈值为4.8×10-4×60%m时,k的上限由1.0×106N/m跳跃到1.2×106N/m,其他参数FN=700 N,μS=0.5,μD=0.3,C=6,v=0.03 m/s,m=2 kg.单线性、双线性和三线性压电执行器的压电堆的振幅、最小滑动摩擦力和黏着摩擦力的比较结果如图10和 11所示.

图10 弹性多线性压电执行器的振幅比较Fig.10 Comparison of amplitude of elastic multilinear piezoelectric actuators

图11 弹性多线性压电执行器的摩擦力比较Fig.11 Comparison of friction force of elastic multilinear piezoelectric actuators

从图10和11可以看出,三线性压电执行器的压电堆的振幅最小,单线性压电执行器的压电堆的振幅最大，从单线性到三线性,最小滑动摩擦力和黏着摩擦力逐渐增大.

3 结 论

1) 提出了一种迭代摩擦模型来求解摩擦力作用下单/多线性压电执行器的振动响应并通过和试验结果比较验证了模型的正确性.

2) 对于弹性单线性压电执行器,压电堆的振幅随着FN,v,μS和C的增加而增大,随着μD的增加而减小.在所研究的几个参数中,按照增加百分比,μS对振幅的影响最大,C对振幅的影响最小.FN和μS越大,最大静摩擦力越大.v越大,板和压电堆之间从黏着转到滑动摩擦的时间越短,滑动摩擦力的最小值越小.μD越大,滑动摩擦力越大.C越大,摩擦力从最大黏着摩擦力转到相同数值的滑动摩擦力的时间越短,从滑动转到黏着状态对应的时间点越小.随着阻尼比的增加,压电堆的振幅逐渐减小.最小黏着和滑动摩擦力随着阻尼比的增加而变大.

3) 对于弹性双线性压电执行器,压电堆的振幅、黏着摩擦力的最小值和对应的转换时间随着阈值的增加而变大.压电堆的振幅随着等效刚度的增大而变大,滑动摩擦力的最小值随着阈值的增加而减小.

4) 对于多线性压电执行器,压电堆的振幅随着压电执行器弹性线性数的增加而减小,最小滑动摩擦力和黏着摩擦力随着弹性线性数的增加而变大.