指向结构化思维的小学数学单元整体教学实践
——以人教版数学六年级下册第三单元“圆柱与圆锥”为例
2022-03-11纪祥荣刘峻豪
■文/纪祥荣 刘峻豪
数学是一种结构性、系统性很强的知识体系。由于各种原因,在小学课程中,学生接收到的知识是孤立、零碎的,存在极大的离散性,缺乏整体结构,如何培养学生结构化思维,是当下小学数学教学中教师应重点关注的问题。在小学数学教学实践中,教师要引导学生通过调动已有的知识经验,探寻问题的基本结构,发掘其中内在关联进行积极建构,以培养学生结构化思维。结构化学习是基于知识整体单元发生与发展的学习,能够展现学生完整的学习过程,促进学生主动的知识建构和方法迁移。结构化思维对教师进行单元整体教学设计具有指导意义。教师运用结构化思维进行单元整体设计,有利于促进学生学科知识结构化的建立,有助于培养学生的推理和拓展能力。本文从笔者的实践经验出发,以人教版数学六年级下册第三单元“圆柱与圆锥”为例,阐述教师基于结构化思维,开展小学数学单元整体教学的方法,以供参考。
一、重视问题驱动学习,调动学生经验
核心问题的驱动能够促进学生深度学习,也能够调动学生从整体上感知知识的来龙去脉,从而调动已有的知识经验,建立清晰的学习方向。教师在教学中应重视问题的整体设计,从以下两个方面入手,帮助学生在已有经验的基础上深入理解知识结构。
(一)问题设计要调动学生的经验基础
在小学数学教学中,教师要关注学生的最近发展区,基于学生已有的经验来进行问题的设计,为学生搭建已有知识与新知识之间的桥梁。这样设计出来的问题情境,既能激发学生的学习兴趣,又对学生具有一定的挑战性,能够吸引学生全面、深入地参与知识探究活动,推动学生深入理解知识结构,帮助学生建立已有经验与新知识之间的联系,提高学生的学习兴趣。
例如,在教学“圆柱的认识”这部分内容之前,教师可以让学生回顾此前学过的长方体、正方体和几何方面的知识,调动学生已有的经验。在此过程中,教师可以通过设计一些测试题,准确把握学生对已有知识的掌握情况。另外,为了让学生对新知识有直观的理解,教师可以运用相关教具或实物来辅助教学。
(二)问题设计要基于问题的内在关联
教师对数学核心问题的设计,要从数学概念的本质出发,要具有一定的整体性和关联性。整体性是指教师设计的问题应该有助于教师的单元整体教学;关联性是指教师的问题设计要关联整个单元的结构,要把握知识之间的联系,力求做到环环相扣,使学生探究知识,理解知识的来龙去脉,感受知识的纵横联系,分析知识的发生与发展过程。例如,教师在本单元的教学中,可以对学生进行结构化思维训练,将图形点动成线、线动成面、面动成体,将未知的问题与学生已有的经验相关联,使学生在推导与转化知识的过程中获得新知识和新经验,并将其内化为自己的数学思想,构建知识结构,强化知识体系,提升数学素养。
二、解读设计教材,建立单元结构
在小学数学单元整体教学中,单元是指依据统摄中心,按学习的逻辑组织起来的、结构化的学习单位,是实现培养学生学科素养目标的一种微型课程,它有助于把零散的思维、知识、信息等按照某种逻辑统摄起来,从而让学生实现有关联和有结构的学习。教师要重视单元整体设计,要以一类相关联的知识为线索,以问题为导向,根据学生的认知基础和规律,制定单元学习主题,确立单元整体目标,设计单元整体活动,开展单元整体评价。教师可以从以下两个方面入手,进行单元整体设计,搭建小学数学学科学习的知识和方法结构,促进学生学科能力的形成和发展。
(一)解读教材内容,发掘内在关联
数学知识是有内在联系的,教师在数学教学过程中,要想实现高效的数学课堂教学,就需要将数学知识进行梳理,帮助学生厘清单元内容各知识点之间的内在关联。
以人教版小学数学六年级下册第六单元“圆柱与圆锥”为例,该单元知识属于图形与几何领域,是小学生在学习“图形与几何”时最后一个单元的内容。该单元内容具体包括圆柱的认识、圆柱的表面积、圆柱的体积、圆锥的认识和圆锥的体积。
教师通过分析可知,本单元的关键知识点就是圆柱与圆锥两大模块。基于此,在本单元的教学中,圆柱表面积的计算方法、圆柱体积的计算方法和圆柱相关公式的推导过程,都必须关联圆柱的基本特征。同样,圆锥的体积计算方法与公式推导,也必须关联圆锥的基本特征。另外,对不规则圆柱和圆锥体的表面积、体积的计算,仍然需要关联圆柱和圆锥的基本特征进行解决。这就要求教师在授课时,要准确解读教材内容,牢牢把握本单元的核心知识,利用知识之间的关联灵活迁移,形成结构化、系统化的课堂教学。
(二)厘清内在关联,建立单元结构
在“圆柱与圆锥”这个单元的教学中,教师基于结构化思维,进行单元整体化教学实践。教师依据教材的主要内容,厘清单元不同知识点之间的内在关联,建立三个单元结构,分为三个课时来进行教学,引导学生进行个性化和自主性探究。
第一课时的内容是圆柱与圆锥的认识。在学习本单元之前,学生在此前已经对平面图形(包括长方形、正方形、三角形、平行四边形、梯形等)和立体图形(包括长方体、正方体)有所了解,而本单元关于圆柱与圆锥的知识,与学生之间掌握的知识具有内在的关联。基于此,教师在授课时,可以先让学生认识组成该图形的要素(包括边、角、底、高、面、底、棱、顶点等),再引导学生分析各要素的特征,启发学生分别从数量特征和关系特征两方面去认识该图形,如面的数量、面的形状、面与面的大小关系等。
第二课时的内容是圆柱与圆锥的表面积。这部分内容的学习要求学生依据表面积概念和立体图形面的特征,去探究表面积的计算方法。因此,教师在教学中,可以先让学生探究圆柱与圆锥是由几部分组成的,并对每一部分进行拆分,然后让学生分析拆分出来的每一部分的面积如何计算,最后让学生把图形所有的表面积整合出来。在此过程中,教师要引导学生调动已有的知识和方法策略,将小学阶段对几何图形表面积的计算方法结构化处理,以实现将学习方法迁移运用、融会贯通的教学目标。
第三课时的内容是圆柱与圆锥的体积。这部分的内容与五年级多边形的面积、六年级圆的面积的计算方法高度关联,都体现了转化的数学思维,即将未知转化为已知,进一步探索出体积的计算公式。教师在指导学生探究的过程中,需要把握结构化思维,抓住新旧图形之间的差异,找准问题的切入点,引导学生掌握知识。
三、整合知识内容,深化单元结构
教师在教学过程中,将同一单元的不同知识点建构起整体关联,进行结构化学习,能够促使学生构建结构化思维,展现学生完整的学习过程,使学生主动进行知识建构和方法迁移。例如,教师在本单元教学过程中,针对问题的设计与内容安排进行探究,将“圆柱与圆锥”单元的学习主题进行重构(见图1),将该单元的知识分为四个学习主题,以促进学生知识结构的搭建。这四个主题分别是圆柱与圆锥的认识、圆柱的表面积、圆柱与圆锥的体积和拓展与提升、整理与复习。这样整合后更有利于学生在掌握知识与方法的基础上,进行知识与方法的迁移,促进学生自主探究。
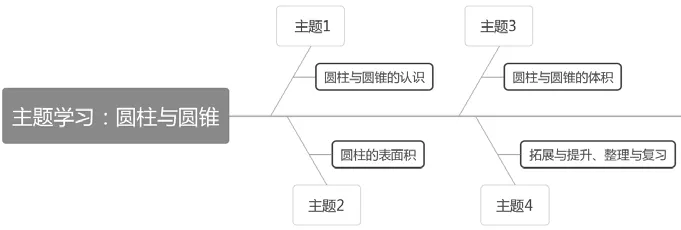
图1
(一)整合探究,在对比中突出学习
在第一个主题“圆柱与圆锥的认识”的教学中,教师整合相关教学资源,对比圆柱和圆锥的探究方法,能让学生对本单元知识的掌握更加深刻。圆柱与圆锥是存在内在关联的,比如通过观察圆柱与圆锥,可以发现其底面和侧面的数量,还有关于高的条数之间的区别:圆柱的其中一个底面变为一个点,就形成了圆锥。此外,通过平面图形的旋转,可以更好地对比两者之间的区别;搭建平面图形与立体图形之间的联系,可以拓展球体等立体图形。教师在对比教学中,归纳总结相关知识,丰富学生对于圆柱与圆锥的认知,既符合数学知识的本质,又增强了学生的数学思维,提升了课堂成效。
(二)设疑促思,在操作中获得新知
在第二个主题“圆柱的表面积”的教学中,为了让学生加深对公式的理解,教师需要在教学过程中设置问题,促进学生思考,使学生在推导公式的过程中发挥想象力。教师在课堂实施过程中,可以引导学生通过观察圆柱的侧面展开图,探究长方形与圆柱底面之间的关系。在此过程中,教师可以设置一些疑问,比如“圆柱的侧面展开图是什么形状?沿着高展开会怎样?得到的长方形与圆柱有什么关系?”,教师通过环环相扣的提问,可以促使学生在推导中获得答案,使学生在探索中获得新知,激发学习兴趣。
(三)类比归纳,在联系中推导公式
主题三“圆柱与圆锥的体积”是本单元重点教学内容之一,在这个主题的设计中,教师需要关注学生核心素养的发展,注重学生对体积计算方法的迁移,培养学生形成系统化、结构化的知识体系,引导学生在理解中类比归纳,推导出解题方法。例如,教师可以引导学生以五年级长方体、正方体的体积概念为基础,以六年级上册圆的面积推导过程为积淀,探讨圆柱与圆锥的体积计算方法,以启迪学生运用转化的数学思维,在动手操作与探究中,推导出圆锥的体积计算公式。
(四)攻难巩重,在拓展中提升
第四个主题是“拓展与提升、整理与复习”。在此阶段的教学中,教师要针对圆柱与圆锥进行单元总结与复习。教师在进行教学时,仍要把握结构化思维,引导学生对难点与重点知识进行巩固。比如,教师可以安排一些应用题让学生进行拓展练习,使学生在理解知识的基础上,把学到的知识转化为能力。这种基于基础知识的变式训练,有助于学生在掌握基础知识的基础上,攻破难点,巩固重点,达成探究目标,完善认知结构。
