农村电商“最后一公里”配送问题的最优模式决策方法研究

杨媚

（乐山职业技术学院 财经管理系,四川 乐山 614000）

一、相关背景

在“互联网+”时代下，农村电商已成为帮扶农产品上行、促使工业品下行、实现乡村振兴战略的重要途径之一。然而因我国农村地理环境、交通不便等诸多限制，这“最后一公里”并未全线打通[1]。2019年上半年，网络购物市场保持较快发展，以中小城市及农村地区为代表的下沉市场拓展了网络消费增长空间，电商平台加快渠道下沉。如何打通“最后一公里”成为亟待解决和优化的问题。

配送的“最后一公里”并不是真正的一公里，是指从物流分拣中心到客户手中这一段距离，通过运输工具等，将货物送至客户手中的过程。这一短距离配送，是整个物流环节的末端环节，也是唯一直接和客户面对面接触的环节，意义重大[2]。物流公司存在配送“最后一公里”这一难题主要原因在于需求量不足、配送成本高、设施不完善等问题，这些问题使得农村地区对于物流公司的生存环境较为“恶劣”，很难盈利，阻碍了物流公司完善最后一公里配送的步伐。

诸涛、倪蔚颖对电商物流“最后一公里”配送中快递收发点菜鸟驿站、社区便利店、快递柜三种目前应用最广泛的模式进行分析，认为具有较大的发展前景[3]。但这三种模式主要应用于城市。王敬斋提出解决电商“最后一公里”问题，并非电商企业和物流公司能够完全解决的问题，需要社会、政府部门参与，政府需要合理规划预留物流发展空间，借助公共交通工具进行物流配送；人人配送、无人配送等也可积极探索[4]。吴向向、王红春提出“快递园”的构建和现场模拟“快递园”的运作方式，利用数据模型预测“快递园”的发展前景[5]。该“快递园”理念也主要针对城市社区。陈婉婷提出以合理的农村电商物流最后一公里配送模式为前提,使用大数据分析技术研究配送路线[6]，但未对主要的配送模式进行分析说明。郭月结合农村电商物流“长运输链＋低消费密度”的特征，提出“选择取送货”模式。物流公司选择部分需求量较大、配送距离较近的农村需求点进行优先配送，最大限度的减少服务盲点，在农村电商物流末端配送网络建设初期，以“物流”拉动“商流”发展，进而实现快递全面下乡的状态[7]。李志鹏研究农村电商物流配送中心的选址问题，主要从配送中心选址的角度出发，考虑每个农村配送需求点可以由多个配送中心共同配送，提高物流速率和成本等，但未考虑货物从配送中心出发后“最后一公里”配送如何实现[8]。丁红英认为提高农村电商物流配送需要优化“最后一公里”配送方法、合理选择配送网点地址、加大农村基础设施建设、培养专业技术型人才[9]，但未给出具体的优化方法、选址方法等。

综上，从相关学者目前对农村电商“最后一公里”研究来看大多站在物流企业（快递公司）的角度考虑，降低物流成本、提高物流企业收益、提高物流速率等，其他因素考虑较少，如，收件人的满意度、收件人取货花费的时间等。同时，对“最后一公里”具体的配送模式研究也较少。因此，从多角度优化“最后一公里”配送方法还有待深入研究。

二、农村电商现有“最后一公里”配送模式及存在问题

在政府政策的支持下，我国农村物流在不断发展，但仍然处在发展初期，以阿里集团、京东、拼多多等为代表的电商公司和以邮政、“四通一达”、顺丰等为代表的物流公司开始向农村地区延伸服务，呈现县乡两级物流服务架构。目前我国乡镇物流覆盖率已达80%,但从现状来看基本止步于乡镇，快递下乡到村一级基本没有实现。当前，农村电商物流“最后一公里”配送存在的主要问题有：配送成本高；基础设备差；配送网点少、选址不合理；缺乏物流专业人才等[9]。从当前“最后一公里”快递配送模式来看目前主要有6种模式，见表1。

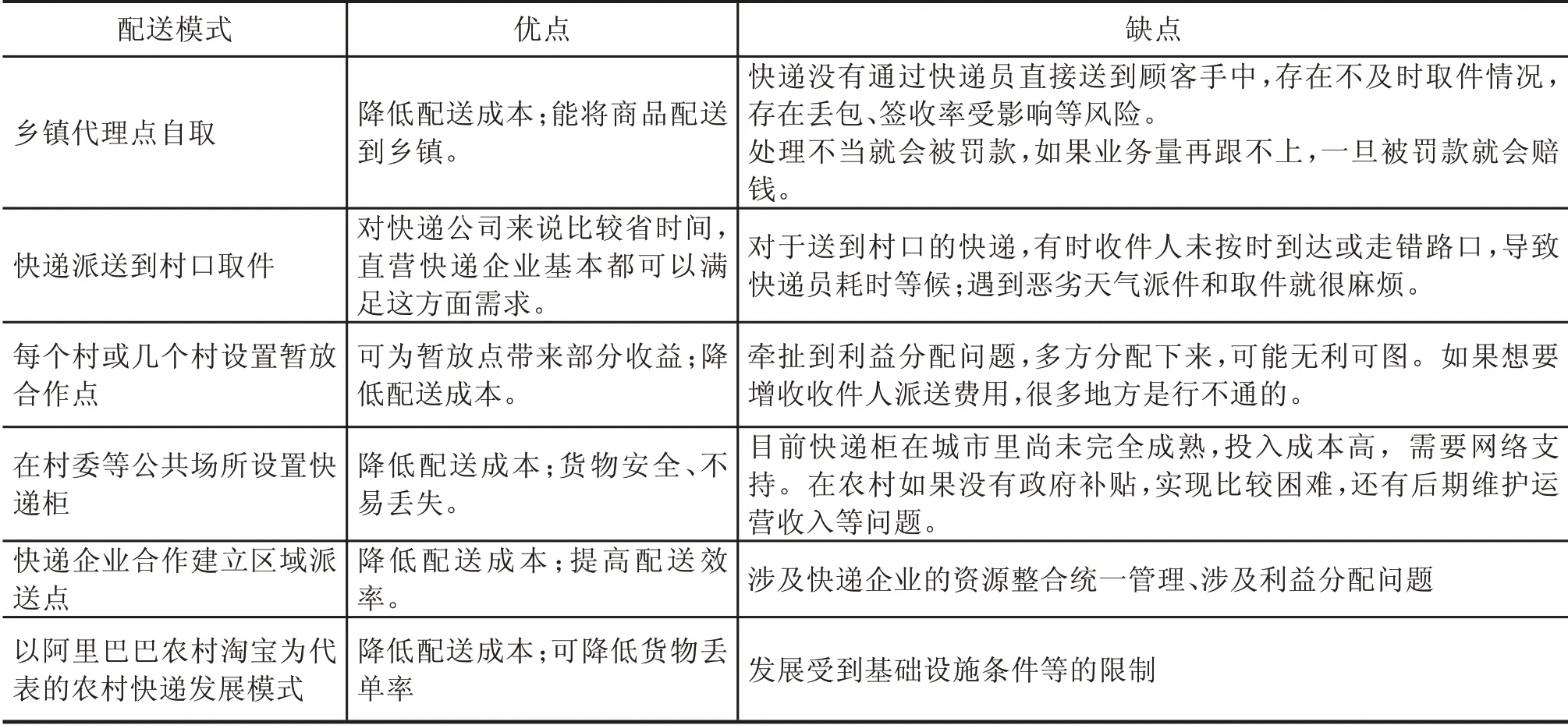
表1 目前农村电商“最后一公里”配送主要模式

从以上主流快递配送模式来看，有其优势（更多的是考虑如何降低配送成本等问题），但同时也存在不少的问题，如：快递丢包率、收件人取件麻烦等。如何从多方面优化农村快递”最后一公里”配送的问题，还有待继续研究。

三、最优配送模式的原理及其方法设计

通过以上分析，本文试图从快递配送收益成本、收件人满意度两个方面进行分析，把“快递园”理念运用到农村电商“最后一公里”配送，构建村民自取点取货模型和快递员统一配送模型，并在此基础上改进“选择取送货模式”，融入“收件人的满意度”构建基于满意度的最优配送模型，从收件人的满意度（主要考虑配送间距）和快递配送收益成本出发，探讨农村电商“最后一公里”配送问题。

（一）最优配送模式内涵

本文中的最优配送模式即从快递配送收益成本和收件人满意度两个方面进行分析，优化收益成本、提高收件人满意度构建配送模型。

1.快递配送收益成本分析

优化配送模式的根本目的是增加收件人的满意度、降低配送成本和增加收益。郭月提出的“选择取货模式”从三个方面来降低配送成本和增加收益[7]。见图1，其中图a为原始收益成本图，可见单位成本大于单位收益，无法获得利润；图b中①增加快递数量可使单位收益大于单位成本，可能获得利润或增加利润；②降低单位成本可使单位收益大于单位成本，可能获得利润或增加利润；③增加单位收益可以使单位收益大于单位成本，可能获得利润或增加利润。通过以上分析得出在其他因素保持不变的情况下，增加快递配送数量或者增加单位配送收益或者降低单位配送成本，可获得利润或增加利润。

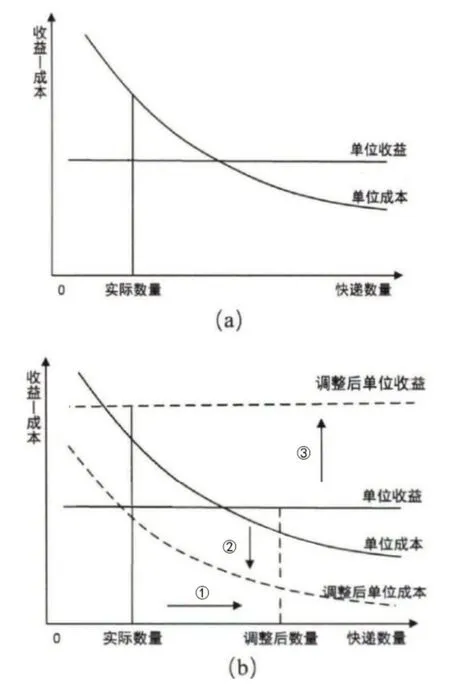
图1 快递配送收益-成本图

2.收件人满意度分析

收件人满意度也就是收件人的满意程度，是对收件人满意水平的一种量化测度。如美国学者Cardozo所言，收件人的期望会影响收件人的满意度，收件人的期望与服务过程中收件人的实际感知之间的差距可用于测量收件人的满意程度。郭媛媛在对物流配送服务农村顾客满意度影响因素研究中发现，物流配送服务的可靠性和保证性对收件人满意度的影响最大，这就要求快递员能够将货物准确、按时、无损地送到顾客的手中，这也是收件人最根本的诉求[10]。石小岑在基于层次分析法对物流配送顾客满意度的评价的研究中表明商品的配送速度和配送质量最能影响收件人的满意度[11]。本文将满意度融入到模型中，提出配送间距与满意度关系（见图2），配送间距即收件人地址与取件地之间的距离。当快递员将货物直接配送到收件人预留地址，视为配送间距为0，则满意度最高，当快递员将货物统一放到乡镇代理自取点或村口等，收件人自行取货，则存在配送间距，则满意度降低。从图2中可见配送间距为②点处的满意度低于配送间距①点处。

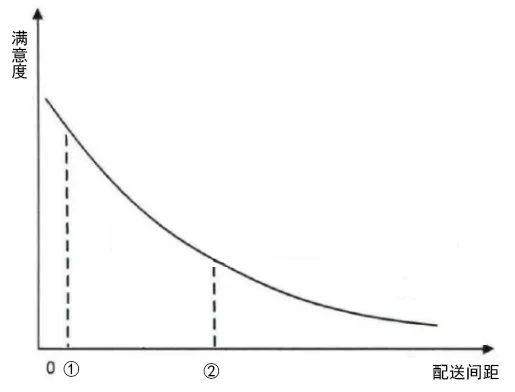
图2 配送间距与满意度关系

（二）模型构建与推理

沿用文献[6]这一理念，把一个村看作一个“快递园”，一个村的面积为E，把村看作一个矩形，长宽值分别为L、W，村里户数为n。为体现满意度及配送模式的差异性，首先构建两个模型，一个是选取最优的快递自取点位置，村民到快递自取点取货的取货模型；另一个是该村派遣一名快递员进行统一配送的模型。在两种配送模型构建的基础上，再构建基于满意度的最优配送模型。

1.村民自取点取货模型

（1）模型构建

村民自家出发去自取点收取快递的时间成本为T j，一次取物量q j，γ为取货量系数，当取货量增加时，γ值下降，γ取值(0,]1。考虑到农村道路复杂，且实际道路并非两点间的直线，设路况复杂程度系数βj，快递自取点的坐标为(x,y),村户的位置坐标为（x j，y j），j的取值1-n,村民最优的快递自取点位置(x,y)，C1为在一个时间段内，需要取件的村民取件的总成本。考虑村民取件总成本，约束条件为村范围、村户数量，建立如下模型：

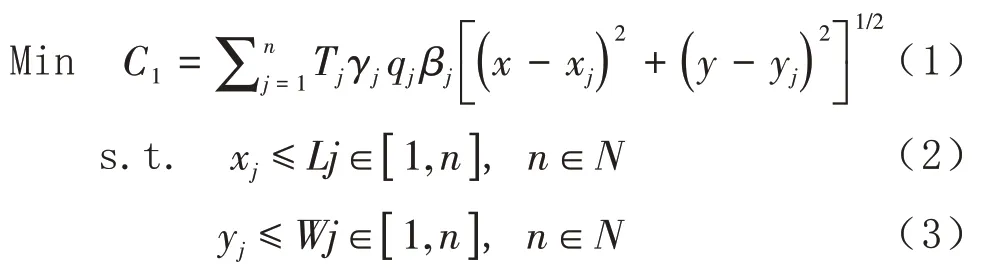
（2）模型求解方法及复杂度

考虑到获得数据结果的精准性，且数据量不大，采用枚举法，通过计算机C语言编程遍历所有可能的结果，两两比较，获得最优点。计算复杂度为n3。

2.快递员统一配送模型

（1）模型构建

快递配送单位费用U i，一次送货量Q i，μ为取货量系数，考虑到农村道路复杂，设路况复杂程度系数αi，最优的配送路线S i（假设最优路线从起点出发，最终又回到起点），C2为为在一个时间段内，一名快递员将需要配送的货物进行配送的总成本。考虑一名快递员配送货物总成本，约束条件为村范围、村户数量，建立如下模型：

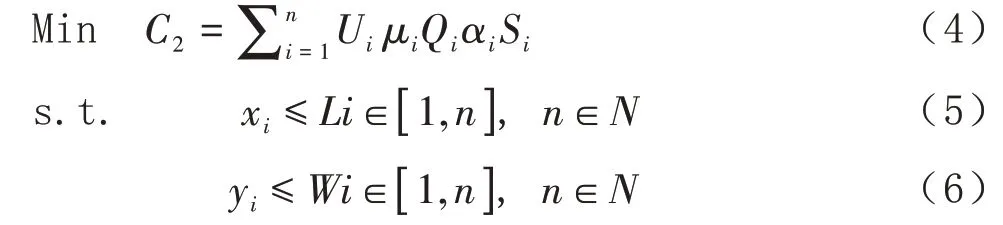
（2）最优配送路线算法及复杂度

最优配送路线实际是通过加权的最短路径算法获得，在已知配送点的情况下，通过计算机语言编程，采用枚举法，获得最小值。计算复杂度为n！。

3.基于满意度的选择性配送模型将满意度与两种配送模型组合，形成选择型取货模型，C为快递员配送总成本，满意度S,村民自取点取货满意度系数为a,nj为自取点取货村民数,n2为快递员统一配送村民数，快递员统一配送满意度系数位b,其他系数同上，模型如下：

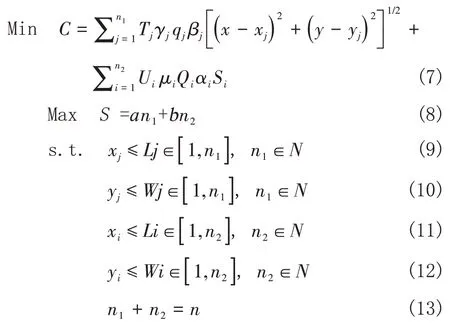
该模型为双目标模型，考虑式（7）为第一目标，式（8）为第二目标，将式（13）带入式（8）得到：

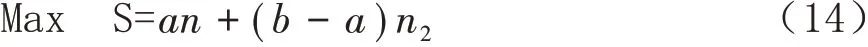
由式（14）分析，如果a、n已知，当b>a，n2越大，则S越大。由此则需要对第一目标式（7）求解。

四、算例分析

通过C语言编程，按照模型计算出在相同大小的村，即村的长宽值L、W固定不变，村面积大概在7.5-15平方千米，为了降低计算的复杂度，在不影响结论的前提下，将村的长L取值3千米、宽W取值4千米，即村面积12平方千米。结合农村实际情况，一个村户数大致在50-500之间，分别取值50、100、200、300、400、500。村民的位置坐标随机产生。由于同一时间段并非所有村民都需要去取快递，故设村民购物取货率10%。假设村民通过自取点取货满意度为1，快递员统一配送村民满意度为2。由式（14）可知，当b>a时，n2=n,即全部采用快递员统一配送，满意度最高，但还需根据式（7），考虑收益成本最大化问题。因此在算例分析时，对三个模型进行分别分析如下：

（一）村民到快递自取点取货

村民居住地的坐标位置（x j，y j）随机产生，取快递的时间成本T j，考虑到村民对时间成本的不同，取值设定在[1,3]，一次取物量q j，取值设为[1,3]，考虑到农村道路复杂，设路况复杂程度系数βj，γ取值：当q j=1时，γ=1；当q j=2时，γ=0.8；当qj=3时，γ=0.6；获得（1）式，约束条件如下：

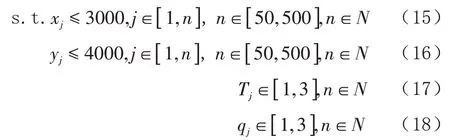
考虑村户坐标点随机产生，故每个相同n值下，重复计算，获得5个数值。通过程序计算得到如下表2数据值信息。

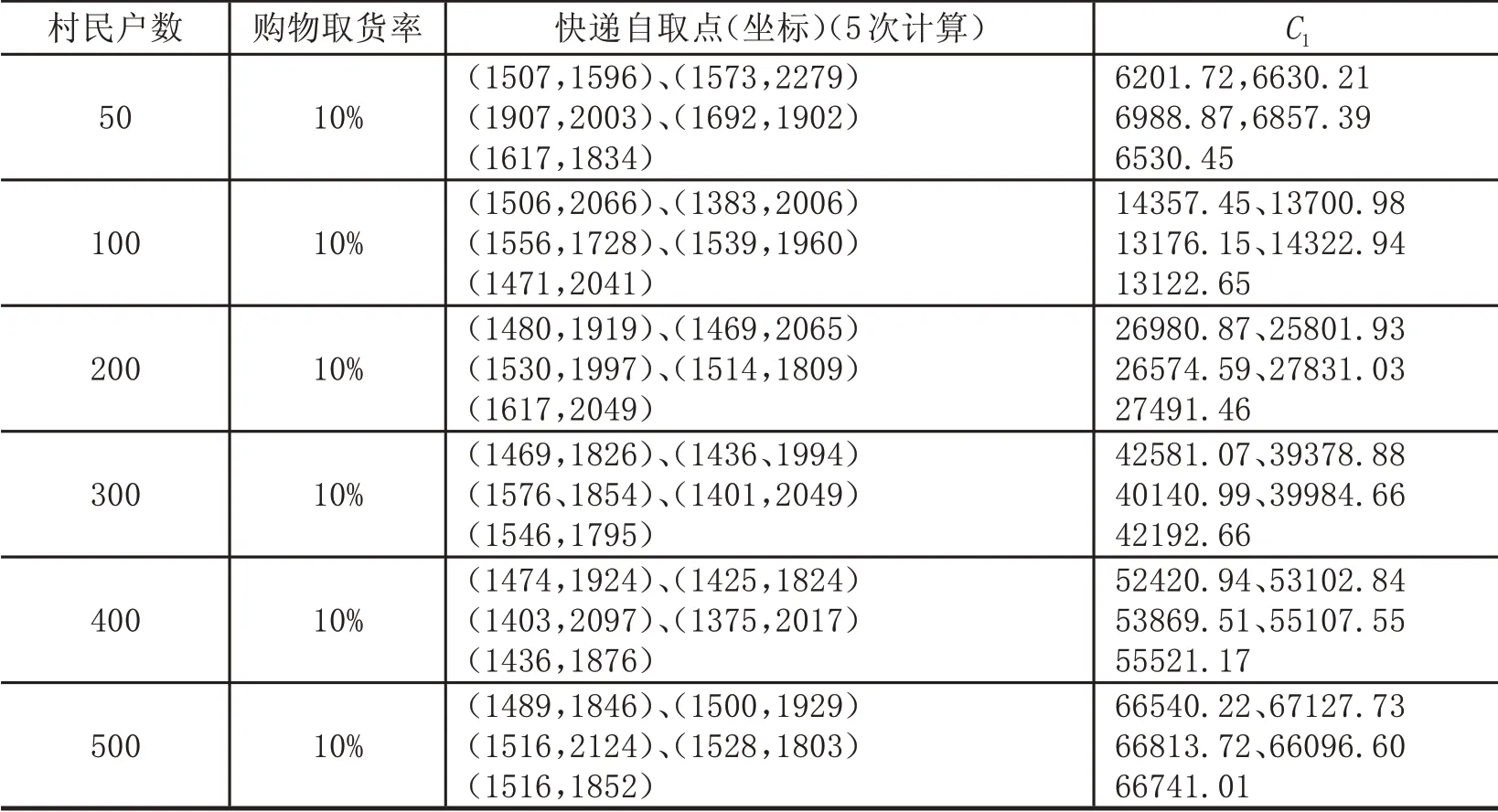
表2 快递自取点最优位置及消费值

通过计算我们对数据进行简单分析，当该村长宽位置固定，通过模型得到的最优快递自取点位置较为集中，在居民户数相同的情况下，得到的消费值也大致相同。即通过此模型可以得到较优的自取点位置。见图3、图4。

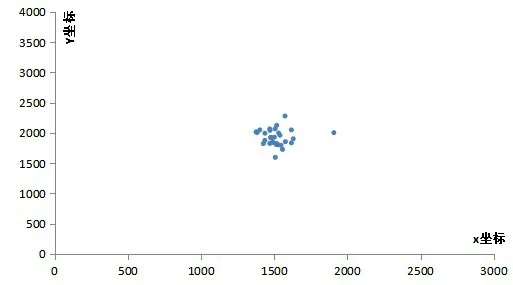
图3 快递自取点最优设置位置

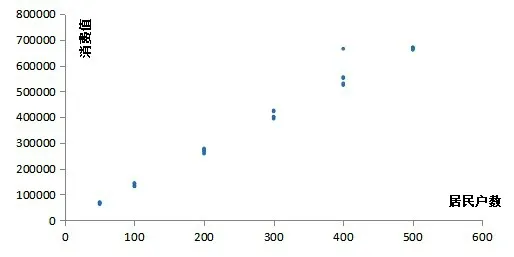
图4 快递自取时居民户数与总成本关系

（二）快递员统一配送

通过语言编程对模型求解且按照最优配送路线算法获得配送路线及C2，如表3。

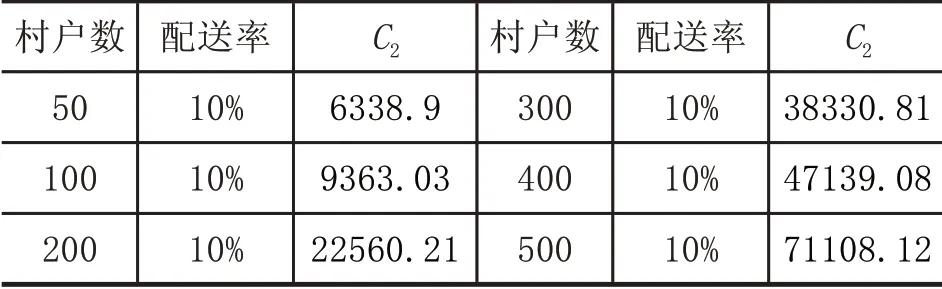
表3 快递员统一配送消费值C2

（三）基于满意度的最优配送模型

通过对模型的分析可知，当n1=n时，式（7）可简化为式（1），得出的结果同上；当n2=n时，式（7）可简化为式（4），得出的结果即同式（4）；求解过程同样通过C语言编程，遍历分组求解，即随机产生村民居住地的坐标位置，C n j n(n j∈[1,2,…,n],n∈N)分组求解获得最优C值，其他参数取值同式（4）和式（1）求解所带参数。对第一目标求解得到式（7）最优解后，再考虑第二目标式（8）满意度，获取的数值见表4。n1取值多个，由于C的取值更多，C取值很多都很接近，为保留更多的n1，故C值保留整数。

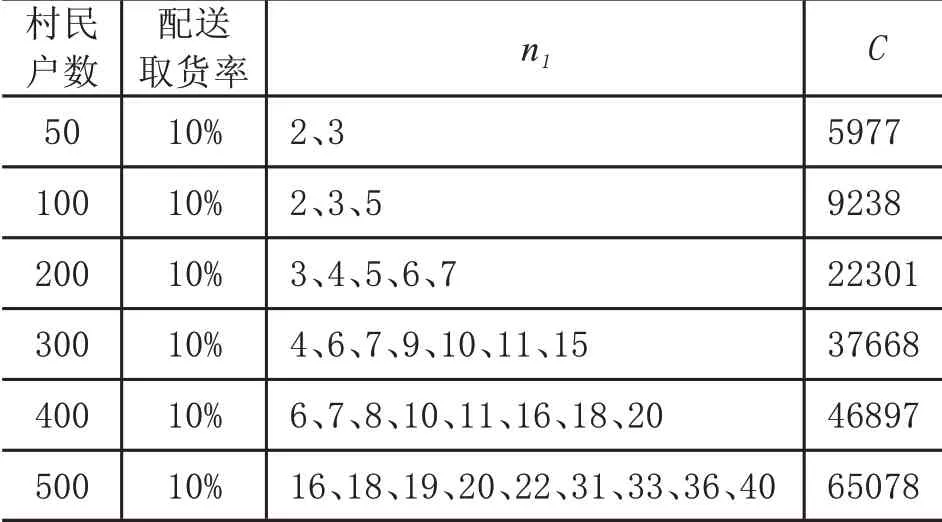
表4 基于满意度的选择配送模型

（四）三个模型对比分析

通过对数据进行分析，在一定条件下通过对村民自取点取货模型求解，可以得到较优的自取点坐标位置；对快递员统一配送模型求解可以得到最优的快递员统一配送路径；该两个模型相比较，当居民户数低于500时，C2低于C1；当居民户数高于500时，C2开始高于C1，由此两种模型不能说哪种模型一定更优，配送人数的不同对消费值有影响。对于基于满意度的最优配送模型融入快递员统一配送模型和村民自取点取货模型以及村民取货的满意度，对该模型求解得到的结果都优于快递员统一配送模型和村民自取点取货模型。见图5。

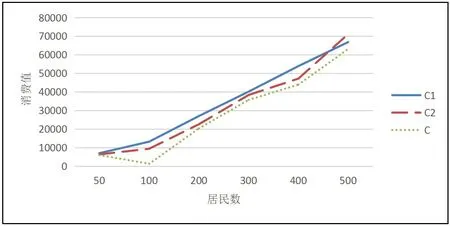
图5 C1、C2、C对比图

五、结论与讨论

构建乡村末端物流线路共享系统，将物流线路终端布置到村一级，实现配送入村全覆盖具有重要的现实意义。本文从收件人的利益和配送成本出发建立快递自取点取货模型和快递员统一配送模型，同时融入取件人的满意度，构建基于满意度的最优配送模型。通过模型构建求解得出：此种模型针对我国农村特殊的地理环境和村民分散居住的特点，结合自取点自取和快递员统一配送两种配送形式进行配送，具有一定的优势，可在农村电商物流“最后一公里”配送中应用。同时，单一的快递自取点取货模型和快递员统一配送模型并不能简单说哪一个模型更优，需结合其他因素才能得出结论。

当然模型的构建和求解还存在一定的局限性，本模型讨论只考虑了一名快递员进行统一配送的单路径问题，多名快递配送的多路径模型还需进一步讨论。在满意度的考虑上，只考虑了取件人与配送间距的满意度问题，影响取件人满意度的因素较多，也可进一步将更多影响取件人满意度的因素融入到最优取件模型中进行讨论。