基于地下铲运机铲斗斗刃位置的工作机构油缸行程解算模型推导及分析验证

2022-03-10高泽宇张元清李恒通

矿冶 2022年1期

高泽宇张元清郭鑫姜勇李恒通

(1.矿冶科技集团有限公司，北京 100160；2.北矿机电科技有限责任公司，北京 100160)

作为智能化矿山的重要技术发展方向的智能铲运机，其远程控制、无人驾驶等技术已经逐步实现了工业应用[1-3]，如今，如何实现自主铲装已成为国内外智能铲运机领域内重要的研究方向[4]。作者所在团队的研究[5]已详细介绍了地下铲运机的工作装置的运动学方程及其验证过程，并实现了铲斗的轨迹跟踪控制，为地下铲运机铲斗的自动化运行奠定了基础。但在智能化控制过程中，铲运机控制系统需要通过分析采集到的料堆数据进行决策，规划生成最优的铲装曲线，再由控制器控制铲斗沿该铲装曲线轨迹进行铲装，以满足满斗率和铲装效率的需求[6]。因此，如何将智能规划的最优铲装曲线转换为跟踪轨迹路径给入控制系统成为一个新的难题。

铲运机的铲斗通常是通过动臂油缸和转斗油缸的伸缩配合，实现铲斗的铲装动作[7]。若忽略杆件的干涉，将铲运机工作装置的运动视为平面运动，本文所研究的KCY-2地下铲运机正转六杆工作机构运动学简图[7]如图1所示。

图1中，各刚体之间的铰接点由A-J表示，B1-B9为组成工作装置的刚体。其中，A、B、C三点与前车架固结，BDIHG为动臂结构，EF为连杆，EH为摇臂，H点为动臂上定点。AD为动臂油缸，CE为转斗油缸，F点和G点为铲斗上的点，J点为铲斗铲尖点。如图1所示，建立参考基坐标系O1X1Y1，及连体基坐标系O2X2Y2、O3X3Y3和O4X4Y4，根据多刚体系统运动学理论进行了运动学分析方法[8]，以及多刚体运动学旋转变换矩阵理论分析，结合各刚体间的位置关系进行矩阵变换，可得铲斗斗刃点J在参考基中位置变换公式[5]，见式1。

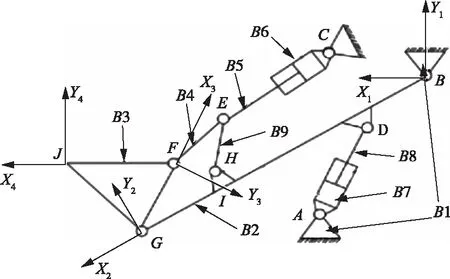
图1 铲运机工作机构二维运动学简图[7]Fig.1 Two-dimensional motion diagram of working device of scraper[7]

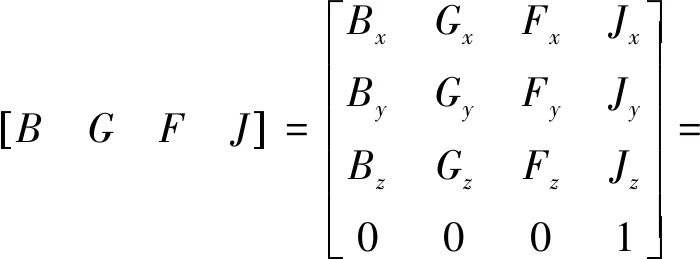
(1)

式中，B、G、F分别为O4的连体基坐标系中的3个坐标轴在参考基坐标系中的坐标表示；J为O4连体基坐标系的原点J在参考基坐标系中的坐标；Lij为点i、j之间的距离，i、j可为图上A-J中互不相同的任意两点。θk为Xk+1与Xk之间的扭角，k的取值为1、2、3。式1所建立的运动学模型可以准确的描述铲尖位置与动臂油缸和转斗油缸行程之间的关系，对于控制动臂油缸和转斗油缸实现规划的铲装轨迹具有重要意义[5]。

在实际控制过程中，当智能铲运机通过料堆识别而规划出最优铲装轨迹后，许多研究者在将规划铲装曲线解算为动臂油缸和转斗油缸的行程时，往往优先考虑对式1进行逆推，但式1所建立的运动学模型中间参变量多，推导过程复杂，因此，通常采用拟合曲线的方法，得到铲尖位置与动臂油缸和转斗油缸之间的关系。这种方法较为简单快捷，但由于没有建立起严格的数学推导过程，所得到的传递函数关系在实际使用过程中存在较大的误差需要校正。同时，拟合关系只能应用于单台设备上，只要换一台设备就需要重新校正拟合，完全不具备普适性。因此，本文基于KCY-2地下铲运机的结构和实车测量数据，对铲运机铲斗斗刃位置关于工作机构油缸行程的解算模型进行了深入研究。

1 斗刃位置关于工作机构油缸行程的解算模型推导

根据图1，铲运机工作装置机构可简化为图2，各刚体结构与铰接点可视为同一平面[9]。

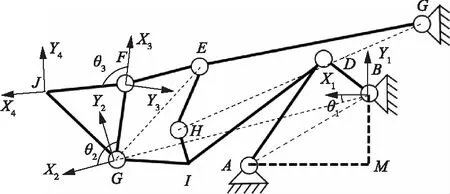
图2 铲运机工作装置机构简化图[9]Fig.2 Simplified diagram of working device of scraper[9]

图2中，点A和点D为动臂油缸的两个铰接点，点C和点E为转斗油缸的两个铰接点。lmn表示点m、n之间的距离，其中，m、n可取为A、B、C、D、E、F、G、H、I、J、M任意一点。点A、点B和点C均为固定铰接点，点M为点A的水平方向与点B的竖直方向的交点，故lAM、lBM、lAB、lBC以及lAC均可测得。BDIGH为动臂结构，通过钢结构焊接连接，因此点B、D、I、H、G之间没有相对运动，故lBG、lBH、lBD、lBI、lDG、lDI、lGI以及lHI均可测得。连杆EF、摇臂EH为固定机构件，故lEF及lEH均可测得。铲斗结构GFJ通过钢结构焊接连接，因此点G、点F和点J之间没有相对运动，故lFG、lGJ以及lFJ均可测得。AD和CE的长度lAD、lCE为：

lAD=l动+x动

lCE=l转+x转

(2)

式2中，l动为动臂油缸缸筒长度，x动为动臂油缸活塞杆行程，l转为转斗油缸缸筒长度，x转为转斗油缸活塞杆行程。

由式1可知，扭角θk是铲尖位置与动臂油缸及转斗油缸行程之间重要的中间变量，即动臂油缸及转斗油缸的行程需先转化为关于θk的函数，才能通过式1计算铲尖位置。因此，在对式1进行逆推求取工作机构油缸行程解算模型时，同样需要扭角θk做为中间变量，建立起铲尖位置到动臂油缸及转斗油缸行程的关系，即由铲尖位置参考基坐标系O1X1Y1下的横纵坐标(Jx,Jy)推导出扭角θk的函数，再通过扭角θk得到动臂油缸及转斗油缸行程的函数。在推导过程中，在不考虑参考基坐标系与连体基坐标系的情况下，所涉及到的所有角αxyz均可视为是某一个三角形Δxyz的内角∠xyz，其中，x,y,z可为A、B、C、D、E、F、G、H、I、J、M任意一点，且x,y,z不可取相同的点。故而对任意αxyz，均有：

0≤αxyz≤π

(3)

因此，对于定义域内任意角度αxyz，其余弦值cos(αxyz)与之一一对应。

1.1 扭角θk关于铲尖位置的数学推导

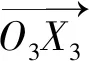
由图2可知：

(4)

式中，αJFG∈[0，π]，故其反余弦函数arccos(αJFG)在值域内有唯一解，即θ3有唯一解。

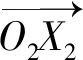
由式1可得：

Jx=lFJcos(θ1+θ2+θ3)+lGFcos(θ1+θ2)+

lBGcos(θ1)

=cosθ1[lFJcos(θ2+θ3)+lGFcosθ2+lBG]-

sinθ1[lFJsin(θ2+θ3)+lGFsinθ2]

(5)

Jy=lFJsin(θ1+θ2+θ3)+lGFsin(θ1+θ2)+

lBGsin(θ1)

=sinθ1[lFJcos(θ2+θ3)+lGFcosθ2+lBG]+

cosθ1[lFJsin(θ2+θ3)+lGFsinθ2]

(6)

则有：

2lFJ·lBG·cos(θ2+θ3)+2lGF·lBG·cos(θ2)

(7)

可得：

(8)

其中：

a1=lFJ·sin(θ3)

a2=lFJ·cos(θ3)+lGF

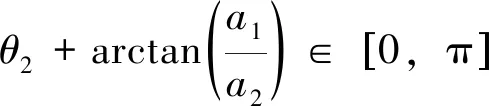
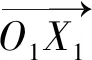
由式6可得：

(9)

其中：

a3=lFJ·sin(θ2+θ3)+lGF·sin(θ2)

a4=lFJ·cos(θ2+θ3)+lGFcos(θ2)+lBG

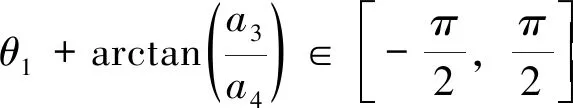
1.2 动臂油缸及转斗油缸行程关于扭角θk的数学推导

由式2可知，动臂油缸的行程x动及转斗油缸行程x转均可通过油缸两铰接点间的距离lAD和lCE来计算。

由图2可见，lAB和lBD为定值，故lAD可通过解三角形ΔABD来计算，可得：

(10)

其中：

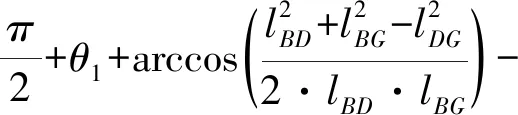
则由式2可得：

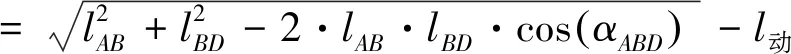
(11)

由图2可见，lCE可通过解三角形ΔCHE来计算，可得：

(12)

其中：

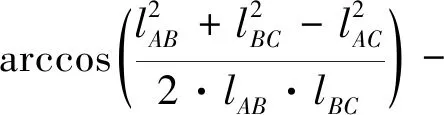
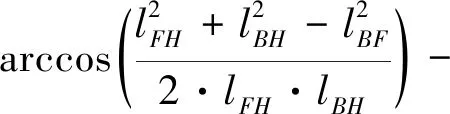
则由式2可得：

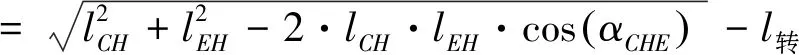
(13)

2 试验与误差分析

在KCY-2地下铲运机实车上，通过实际测量结构尺寸计算可知，扭角θ1∈[-90°，43°]，θ2∈[80.5°，217°]时，θ1与θ2同时有唯一解。实际测量θ1与θ2的极限值，均在上述定义域内，即解算模型在工作范围内，对每一个铲尖坐标J，有唯一对应解(x动,x转)，故模型可直接用于KCY-2地下铲运机。通过实验测量，得到铲运机铲斗在不同位置时铲尖在参考基坐标系O1X1Y1下的坐标(Jx,Jy)，及与之相对应的动臂油缸行程x动和转斗油缸行程x转。将实车测量的铲尖坐标带入上述模型中，可以得到动臂油缸的行程x动和转斗油缸的行程x转的理论计算值。在实车上选取50组铲斗位置，测量数据与模型仿真数据见表1。

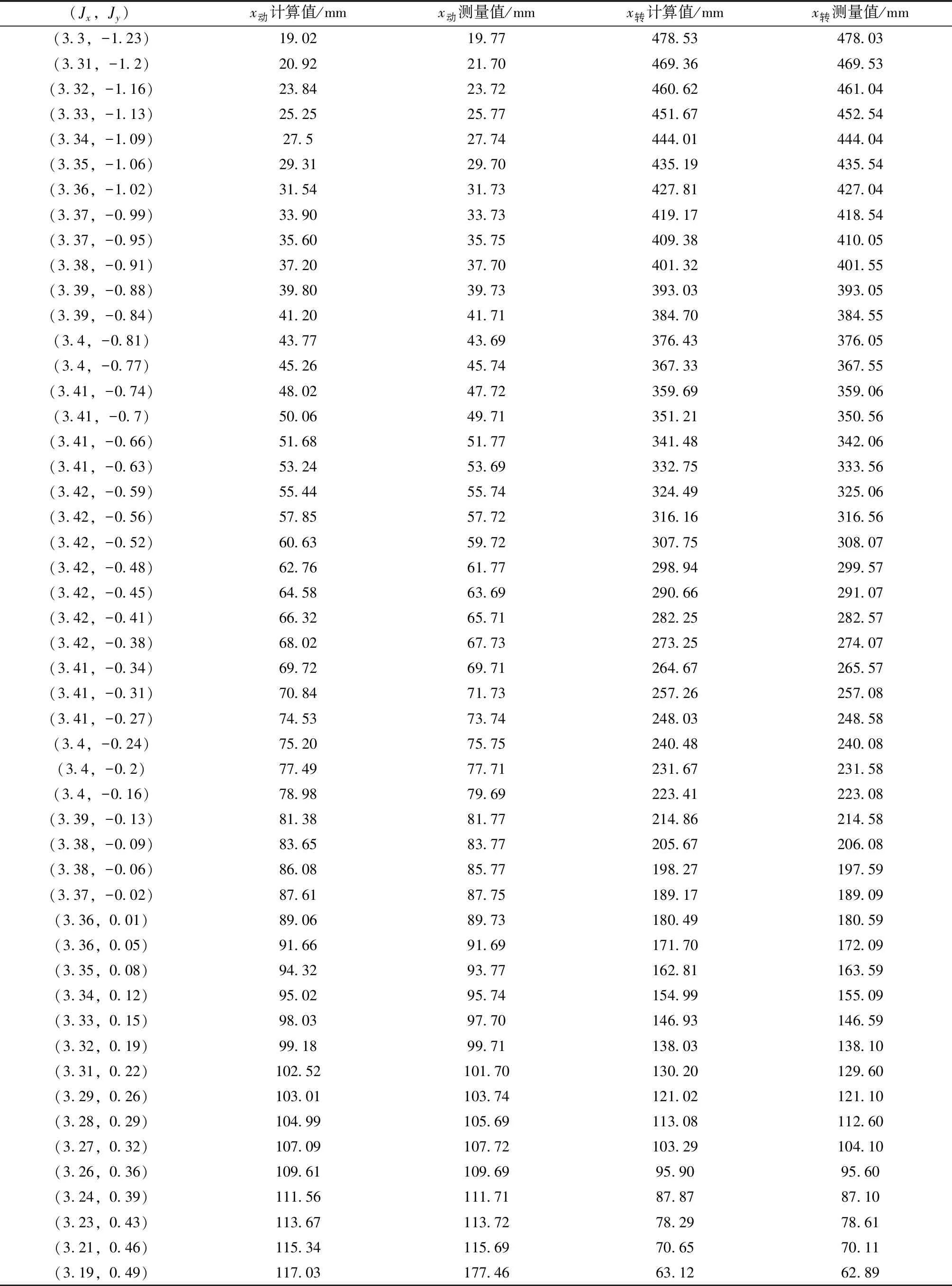
表1 实车测量与模型仿真数据Table 1 Data of the real vehicle measurement and model simulation

以次数n代表第n个铲尖位置，做次数n与动臂油缸的行程x动和转斗油缸的行程x转的实车测量与模型仿真数据图，如图3所示。

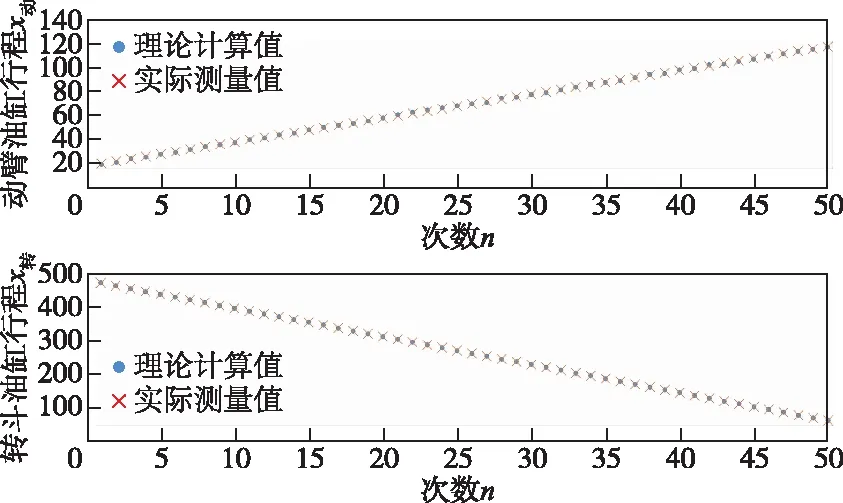
图3 次数n与动臂油缸的行程x动和转斗油缸的行程x转的实车测量与模型仿真数据图Fig.3 Diagram of times with lifting cylinder and bucket cylinder from the real vehicle measurement and model simulation

对动臂油缸的行程x动和转斗油缸的行程x转的进行误差分析[10-12]，x动和x转的残差分布如图4所示。

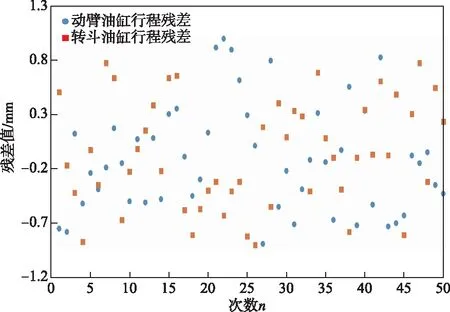
图4 动臂油缸的行程x动和转斗油缸的行程x转的残差分布图Fig.4 The residual distribution diagram of lifting cylinder and bucket cylinder

从图4可以看出，x动和x转的各残差值在y=0时随机分布，存在有随机误差。造成误差的主要原因有两个：1)解算模型是通过设计尺寸建立的，而实车相对于设计尺寸存在有加工误差和装配误差；2)在数据测量的过程中，由于环境、仪器和人员问题，还存在有测量误差。通过计算，x动的最大残差值为0.99 mm，残余标准误差为0.52，最大相对误差为1.61%。x转的最大残差值为0.89 mm，残余标准误差为0.51，最大相对误差为0.34%。因此，x动和x转的随机误差均可忽略不计。