中介参与下科技成果转化的三方利益分配研究
——基于Myerson值法
2022-03-08单而芳田晓敏吴桂鑫
单而芳 田晓敏 吴桂鑫
(上海大学 管理学院,上海 200444)
在知识经济时代,一个国家的发展离不开科技的进步,而科技水平的提升则需要整个国家创新网络系统中不同主体的自主创新、主体之间的协同创新以及科技成果的转移与转化。作为科技成果转化及知识转移的重要媒介与平台,科技中介是我国创新体系的重要组成部分,它是活动在技术创新市场主体之间,利用自身资源,为了达到创新成功的目的,展开沟通、联系、组织和协调等活动,并提供专业服务的组织机构。在科技中介服务机构运作过程中包括三个利益主体:科技中介服务机构、技术需求方和技术供给方。在三方的合作过程中,科技中介的加入无疑能够在一定程度上规避技术创新中的信息不对称、道德风险等问题,从而减少其交易成本及损失。如果各方能够恪尽职守,毋庸置疑三方都是受益者。对于技术供给方而言,需要得到技术创新和创业的收益,而技术需求方需要获得技术进步带来的收益,同时科技中介需要得到提供服务的报酬,这样三方才能来维护共同的利益。因此,为了形成更加稳定的合作,充分发挥科技中介的作用,公平合理地分配各方的利益就显得至关重要。
1 文献综述与研究思路
1.1 文献综述
目前,大多学者对科技中介的研究主要集中在其概念、类型、功能和建设等四个方面,对于有科技中介参与合作的情况下,如何分配各方利益的研究并不是很多。在已有的文献中,蒋浩等利用无限次讨价还价博弈模型首次提出了三方的利益分配机制。张铁男等利用两两博弈分析,探讨了三方合作过程中的利益关系。常悦等基于鲁宾斯坦三阶段讨价还价博弈模型,探究了有无中介参与前后的技术供给者与潜在采纳者的收益并进行对比分析,指出了中介机构存在的必要性。李柏洲等将中介组织纳入产学研合作型企业原始创新收益分配的主体,采用Shapley值分析了各方之间的收益分配机制。吴洁等根据企业不同的心理压力,首先构建了联盟双方企业之间的讨价还价模型,其次又建立了有中介参与的博弈模型,分析和讨论了合作三方收益变化的影响因素及策略选择。此外,华冬芳等运用演化博弈理论,引入信任、信息共享要素变量分析了科技中介对技术供需方的动态关系影响。
1.2 研究思路
通过以上分析发现,虽然对有科技中介参与的情况下,各方利益分配问题的研究不断深入,但还存在一些不足之处,具体表现在以下方面:一是总体上对于其利益分配的公平合理性这一部分研究的不多,而且对于具体利益分配方案的构建缺乏一定的分析。二是多数学者主要是从非合作博弈模型的角度来探究各方的利益关系,其强调的重点是个体的最优决策,其结果在整体上不一定是有效率的。与非合作博弈不同的是,合作博弈强调的是集体理性、公平和效率。尽管有的文献利用合作博弈的Shapley值分析了三方之间的收益分配机制,然而使用Shapley值的前提是三方的任意两方均能形成联盟,这与实际中技术供需方为避免法律风险和提高效率而避免直接进行联盟是相悖的。考虑到在现实中由于受到各种因素的制约,并不是所有参与者之间都能形成所谓的“可行联盟”而进行合作,诺贝尔经济奖得主Myerson将Shapley值推广到具有网络合作结构的环境中,提出了一个重要的分配规则,也就是Myerson值。此外,González-Arangüena等引入了组间Myerson值和组内Myerson值,以区分每个参与者与其他参与者(包括他在内的联盟)合作的收益,以及他作为其他参与者的中介所获得的收益。Manuel等分析了边际贡献与组内、组间Myerson值和Myerson值三者之间的关系,因此通过计算科技中介的组内、组间Myerson值可以更加清楚地了解科技中介对联盟具体的贡献,从而充分发挥中介的作用。三是虽然已有学者利用纳什均衡法对三方博弈过程中的收益关系进行了分析,但主要采取两两博弈的方式或者只考虑供需两方的收益而忽视了中介的利益,然而中介的尽职与否也是促进合作的必要因素,中介的利益不容忽视。
实际上,科技中介、技术需求方和技术供给方的合作可以看作是科技创新体系网络,在这个网络中技术供、需方均需要借助科技中介来完成合作,而不能脱离中介直接进行联盟。为此,本文旨在选择合作博弈中的Myerson值来分析三方之间的利益分配问题,同时与非合作博弈中的纳什均衡解进行对比分析,最后通过计算科技中介的组内Myerson值和组间Myerson值分析其在联盟中的具体贡献,从而可以充分发挥中介的作用,使联盟更加稳定。
2 预备知识
2.1 合作博弈和Shapley值
效用可转移合作博弈,简称为TU-博弈,可用二元组(N,v)表示,其中N={1,2,…,n}表示参与者的集合,v是特征函数,它是定义在N的子集族上的函数。N的每个非空子集S被称为一个联盟,而称N为大联盟,v(S)表示联盟S中的参与者合作所产生的效用。将所有TU-博弈的集合记为GN。
对于任意的S⊆N,一致博弈(N,uS)定义为:如果S⊆T,则uS(T)=1,否则uS(T)=0。对于任意TU-博弈(N,v),特征函数v可以表示为一致博弈的线性组合,也即
v=∑φ≠S⊆NλS(v)uS
(1)
这里
λS(v)=∑φ≠T⊆S)(-1)|S|-|T|v(T)
(2)
它表示联盟S所产生的红利。支付向量x=(x1,x2,…,xn)∈Rn表示每个参与者i分配到的收益为xi。TU-博弈的分配规则或值是定义在GN上的一个函数f,也即每个TU-博弈对应一个支付向量f(N,v)∈Rn。在TU-博弈中Shapley值是最著名的有效值,其定义为
(3)
这个定义说明参与者i的Shapley值等于i参加不同联盟所均分得到的红利之和。
2.2 图博弈与Myerson值
1977年,Myerson将Shapley值推广到网络通讯环境中。具有网络结构的合作博弈(简称为图博弈)由一个三元组(N,v,L)所组成,其中(N,L)为图,而(N,v)为TU-博弈。在图(N,L)中,顶点集N代表参与者的集合,而边集LL^N={{i,j}|i,jN,i≠j},每条边由一个无序对组成,每条边表示两个参与者之间的双边通讯关系。通常以L来表示图(N,L)。
如果图中的两个点i和j通过一系列边相连,则称i和j是连通的,若图中任意两个点都是连通的,则称图(N,L)是连通的。对于任意非空集合S⊆N,L(S)={{ij}∈L:i,j∈S}称为由联盟S导出的子图。若L(S)是连通的,则称联盟S是连通的。如果子图L(S)是连通的,但对于任意j∈NS,子图L(S∪{j})是不连通的,则称S是图L的一个分支,分支的集合形成了N的一个划分,记图中所有分支的集合为N/L。特别地,对S⊆N,用S/L表示L(S)中所有连通分支的集合。
Myerson假定只有连通的联盟才能形成可行联盟,而不连通的联盟S获得的效用等于L(S)中各个分支收益之和。由此Myerson定义了的图限制博弈(N,vL):
vL(S)=∑R∈S/Lv(R),∀S⊆N
(4)
对于任意图博弈(v,L),它的Myerson值定义为vL的Shapley值,即
μ(N,v,L)=Sh(N,vL)
(5)
不难验证,当L是完全图时,即L=LN时,Myerson值即为Shapley值。
核心是合作博弈中一类满足稳定性的重要解集,它满足联盟理性。所谓满足联盟理性是指任何参与者和联盟都不能离开大联盟而受益。如果一个分配方案在核心中,那么这个分配被称为稳定的。图博弈中的核心定义为:
C(v,L)={x∈Rn|x(N)=v(N),x(S)≥vL(S)}
(6)
其中x=(x1,x2,…,xn)∈Rn表示一个支付向量,x(S)=∑i∈Sxi。
2.3 组内Myerson值和组间Myerson值
在图中,一个参与者与其余参与者联系越紧密,其通讯能力越强。在用Myerson值进行收益分配时,每个参与者所分配的收益与其通讯能力和自身对联盟的贡献有关。为了区分两部分的收益,González-Arangüena等根据可加性分解思想,将Myerson值分解为组内Myerson值和组间Myerson值,并给出了以下定义。
一个参与者i从其所处的联盟S中获得的收益,也就是i由于是联盟S的一员,与S中其他参与者合作所分配到的收益,称为组内Myerson值μW,计算公式为:
(7)
其中对于任意参与者i∈N,
(8)
组内Myerson值体现了参与者由于是联盟中的一员所对应的收益。
若一个参与者i不参与形成某一个联盟S,但其在S的形成中却有必要的连通作用,则该参与者i在他不属于的联盟中充当中介而获得的收益,称为组间Myerson值μB,计算公式为:
(9)
其中v-i=v-vi。
3 问题描述与模型的构建
3.1 问题描述
科技中介在运作过程中包括三个利益主体:技术供给方、技术需求方和科技中介。基于接下来的分析,首先作出如下假设:
技术供给方S的技术创新成本为0.5kI2(I是一个可以估算的创新成本常量,k为技术研发难度系数,k>1),搜寻技术需求方的成本为Cs,技术需求方每销售一单位产品需向技术供给方支付Ps的技术价格,供给方的收益为Es;
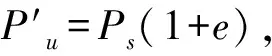
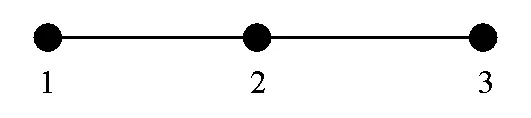
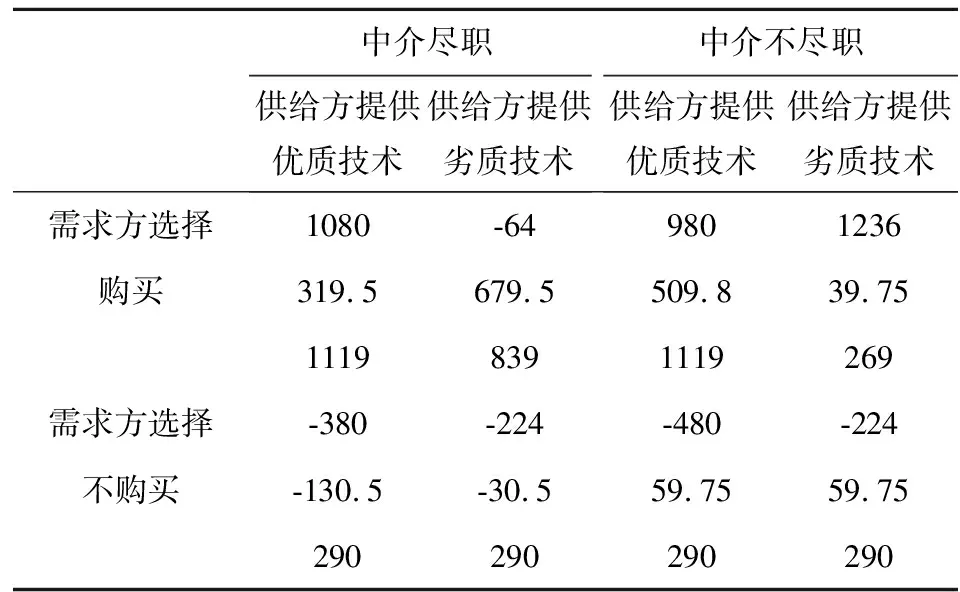
科技中介M的搜寻成本为0.5θy2(y为一个可以估算的中介搜寻成本,θ(0≤θ≤1)为中介尽职的程度),中介费用为Pm,Pm 为简化模型,进一步做出如下假定: (4)供给方有两种策略可以选择:提供优质技术和提供劣质技术,技术创新成本分别为0.5k1I2和0.5k2I2;需求方也有两种策略可以选择:选择购买和选择不购买。 (5)科技中介两种策略可以选择:尽职和不尽职搜寻信息,其成本分别为0.5θ1y2和0.5θ2y2。 (6)若科技中介尽职搜寻信息,发现技术供给方向需求方提供劣质技术,则技术供给方会受到惩罚,罚金为F,该罚金会高于其收益,然后这部分罚金分别按比例λ(0≤λ≤1)和1-λ补偿给技术需求方和中介;但如果技术供给方提供优质技术,则会为其提供信誉奖励R,若科技中介不尽职搜寻信息,则科技中介需要因其不作为给予损失方补偿h。 (7)在技术交易市场中,技术需求方是完全劣势方,即使技术供给方提供了优质技术,但技术需求方仍然可能因技术与自身企业特征不能完全匹配而放弃购买。此时,科技中介在技术需求方决定不购买技术后则会按一定比例β退还其所缴纳的中介费用,而当技术需求方选择不购买时,技术供给方无需支付中介费用。 本文涉及的符号及含义见表1。由此可得三方博弈模型(如表2.1、2.2所示),博弈矩阵中的收益按行分别对应技术供给方、中介、技术需求方。 表1 符号及含义 表2.1 博弈策略矩阵 表2.2 博弈策略矩阵 正如前面提到的,合作博弈强调的是在契约下,为了共同的利益,通常参与者各方将选择对促进合作和提高整体利益有利的策略,即技术供给方会选择提供优质技术,中介选择尽职搜寻信息,技术需求方选择购买,以此来实现合作效益最大化。 下面我们用合作博弈模型重新描述上述的问题。考虑三方合作博弈(N,v),N={1,2,3},其中参与者1,2,3分别代表技术供给方,中介和技术需求方。三方合作关系为:技术供给方与需求方为规避技术创新合作主体的信息不对称和法律风险等问题只通过中介联系,因此三方合作的关系图可以设为L1={{1,2}, {2,3}},如图1所示。 图1 (N,L1) 将其搜寻成本的降低及利润的增加设为收益值v,为此收益特征函数v可以定义如下: v({1})=v({2})=0,即技术供给方、科技中介单独行动时收益分别为0; v({3})=440,即技术需求方未应用创新技术前的收益为(28-24)×110; v({2,3})=440,技术需求方仅与中介合作,而无技术供给方参与,此时合作的收益仍为440; v({1,2})=0,即中介与技术供给方合作时联盟收益为0; v({1,3})=1999,即技术供需方合作时联盟收益为(16×1.9-24+22.5)×110-480-370-330; v({1,2,3})=2518.5,即三方合作不仅使三方总体的收益增加为(30.4-24+22.5)×110-480-370-330,而且降低了搜寻成本370+330-0.5×192; 因此,合作博弈的特征函数v可以表示为: 由(1)-(5)式计算得:v=440u{3}+1559u{1,3}+519.5uN,vL1=440u{3}+2078.5uN。 按照Myerson值的定义,计算可得三方各自分配的利益: μ(N,v,L1)=Sh(N,vL1)=(692.8, 692.8, 1132.8)。 下面说明上述所得的Myerson值在核心中,由核心的定义(见(6)式)容易验证:对于任意的S⊆N,∑i∈Sxi≥vL1(S)成立,这说明Myerson值是一个稳定解。 最后,通过(7)-(9)式计算分别可以得到中介在(N,v,L1)情形下的组内Myerson值和组间Myerson值: μ2(N,v,L1)=μ2(N,440u{3}+1559u{1,3}+519.5u{1,2,3},L1)=Sh2(N,vL1)=Sh2(N,440u{3}+2078.5u{1,2,3})=692.8 根据3.2节给出的博弈矩阵,通过计算得到以下博弈矩阵,其收益按行分别对应技术供给方、中介和技术需求方。 通过表3得出,在非合作博弈中纳什均衡解为(-224,59.75,290),在合作博弈中由Myerson值计算得出的分配方案为(692.8,692.8,1132.8)。可以看到,由Myerson值计算得出的分配方案不仅可以使整体利益增加,而且各自的收益都会相应的提高。此外,Myerson值给出的分配方案位于核心内,即没有参与者有动机离开大联盟,因此以Myerson值作为分配方案可以使三方合作更加稳定,而在三方合作过程中,中介的作用尤其重要,最后通过计算中介的组间、组内Myerson值可以发现,中介所获得的收益分为在技术供需方之间作为中介发挥的连通作用所获得的收益和其本身可以为联盟带来的边际贡献所获得的收益,其本身为联盟带来的边际贡献越大和作为中介的沟通能力越强,则收益会越高。 表3 博弈策略矩阵 本文首先构建了在科技成果转化过程中三方利益主体的博弈模型,然后运用合作博弈中的重要分配规则Myerson值对三方的收益进行了分配,并与非合作博弈中的纳什均衡解做了比较分析。比较发现:由Myerson值给出的分配方案在公平合理的原则下可以使三方整体利益大幅提高,同时也使得各参与者获得了更高的收益,产生“合作共赢”的局面,从而使合作更具稳定性和可持续性,避免了非合作博弈以个体理性为中心的恶性竞争,最后通过计算中介的组内Myerson值和组间Myerson值分析了中介在三方合作过程中的具体贡献,表明中介不仅要充分发挥在技术供、需方之间的连通作用,也要重视其本身可以为三方合作带来的边际贡献。 我国政府为促进技术转化为生产力,推出了一系列相关政策法规,如税收补贴等,可以将其有利政策加入研究中。在科技中介服务机构运行过程中,科技中介参与合作的程度如何,对于技术供、需方产生的交易成本和风险是不同的,因此可以考虑把不确定因素和风险因素纳入到特征函数中,以体现风险因素对合作带来的负面影响。此外,在现实中,通常存在多个技术供需方和科技中介,由此形成复杂网络。在复杂网络环境下,如何考虑由合作博弈模型的Myerson值来确定分配方案也是需要进一步研究的问题。3.2 模型的假设和构建


4 算例分析
4.1 基于Myerson值的收益分配方案

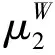
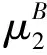
4.2 与纳什均衡解的比较分析
5 结论
