实时竞价中的佣金率问题研究

（河北地质大学，河北 石家庄 050031）

一、引言

从被动投放到主动选择，新型的实时竞价（RTB）互联网广告模式正逐渐成为一种趋势。近些年互联网巨头纷纷进入使得实时竞价广告迅速发展。2012年全球通过RTB模式投放的展示广告金额高达19亿美元。据IDC预测，到2015年基于RTB的展示广告将实现飞跃式发展，其中美国的增长率将达到71%，德国增长99%，法国增长103%，英国增长114%[1]。同时在国内RTB也是飞速增长，自2012年RTB广告模式踏进中国市场只占据0.3%的市场份额，今年起将发展到1%到1.5%，预计明年将会达到3%至5%。

在搜索广告中主要的参与者是搜索引擎和广告主，而在 RTB广告产业链上需要四方合作，首先需要供应方（SSP）提供广告位资源，即广告投放平台；其次是需求方（DSP），即需要投放广告的主体；把供需双方联系到一起需要广告交易平台（AD Exchange）以及数据管理平台（DMP）。本文为了简化模型把中间环节看成全部由（AD Exchange）来完成。由于中间环节的第三方的出现，启发把传统物品拍卖中的佣金率引入到RTB模型中，从而可以从理论的角度对RTB广告模式中各方的策略、收益展开研究。已有学者传统拍卖中的佣金问题进行了研究[2]，同时也有对关键词广告中的保留价的研究[3-6]。拍卖的机制设计在网络广告中已有广泛的应用。随着互联网的发展，互联网广告由展示性广告发展到关键词广告，再到实事竞价广告。关于互联网广告机制研究已有很多的成果，本文给出了在固定佣金率以及线性佣金率（报价越高佣金率越低）时需求方（DSP）的报价策略，并且证明了在无保留价时，需求方的期望支出与任何形式的佣金率无关，佣金率的存在只是改变了均衡的报价策略。随后论文对既有保留价又有佣金率的情况进行阐述，指出在保留价存在时需求方的期望支出与佣金率相关，佣金率增加时需求方的期望支出增加[7]。即保留价存在时，需求方无通过调整自己的均衡报价来对冲佣金率的提高对自己的期望损失。最后论文分别假定保留价和佣金率为外生给定，得出了最优佣金率和最优保留价满足的条件[8]。

二、模型的基本假设

A1、论文模型考虑的是一次静态博弈。

A2、此广告展示平台有k 个广告位，同时n个广告需求方。

A3、广告的供给方、需求方、交易平台都是风险中性，即各方的目标是最大化自己的期望收益。

A4、需求方是对称的，即需求方对每次曝光展示的估价是独立同分布。

A5、令vi表示需求方i 对单次曝光展示的估价，vi在区间[0,1]服从连续可微的概率分布函数F (·)，相应的密度函数为f (·)，且满足F (0)=0，F (1)=1。

A7、令αj表示在第j个广告位的点击率，且点击率只与广告位有关，与在此位展示的广告无关。

A8、以上假设均是共同知识。

三、主要的结论

（一）无保留价只有固定佣金

命题1 在实时竞价过程中，若广告交易平台采用固定佣金c 时，则需求方的均衡投标策略为

证明 考虑典型的需求方i ，它对某广告平台的某次展示的估价为v。假设其它需求方都采用对称的竞价策略b (·)，而需求方i 的报价为b (z)，则i 得期望收益为

对上式关于z 求一阶条件可得

对（4）式整理可得

对（5）式从0到v 积分，并由b (0)=0可得

对（6）式整理可得均衡的报价策略

由命题1容易得到均衡的报价策略b(v,c)关于估价单调递增，从而保证了实时竞价的有效性；同时报价策略关于佣金率c是单调递减函数，即需求方会根据佣金率的变化调整自己最优的报价。

下面分别计算广告供给方、广告交易平台、广告需求方的期望收益。令广告的展示平台的期望收益为RSSP，则

对上式的前半部分使用分部积分，对后半部分交换积分变量的积分次序可得

对（7）式计算整理可得

对（8）式中的最后一项再用分部积分可以得到

从（9）式很容易得到广告展示平台的期望收益关于佣金率递减，即佣金率越高期望收益越低[12]。

下面给出广告交易平台的期望收益RAD，由RAD=cRSSP可得

上式（10）表明广告交易平台的期望收益随着佣金率的提高而增加。

最后计算需求方的期望支付PDSP

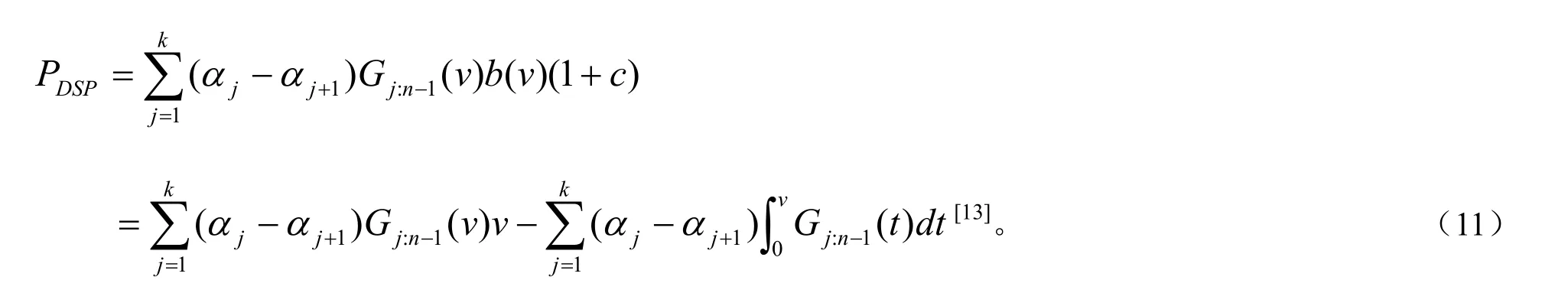
发现需求方的期望支付与佣金率没有关系，即佣金率的大小变化不影响需求方的期望支付。如果佣金率不是固定的值，而是报价的线性函数即c=k0-k1b，其中k0，k1＞0，并且k0是所能要求达到的最大佣金率。直觉上有线性佣金率鼓励需求方报高价来减小佣金，从而减小支出。下面计算线性佣金率的前提下需求方的期望支出。假设其它需求方都采用对称的竞价策略bL(·)，而估计为v 需求方i 的报价为bL(z)，则i 得期望收益为

类似固定佣金的求解过程可以得到均衡的报价策略

由均衡的报价策略可得需求方的期望支付

由（14）可以看到线性佣金率时，需求方的期望支付也与佣金率无关。由此断言需求方的期望支付与佣金率无关。

命题2在实时竞价过程中，如果没有保留价则需求方的期望支付与任何形式的佣金率无关。证明 令E[ p (v)]表示估价为v 的典型需求方i 的在某佣金率下的期望支付，同时其期望所得为

于是均衡时需求方i 的期望收益满足

由积分包络定理可得

再由E[p (0)]=0可得

所以由（18）可得需求方的期望支付与任何形式的佣金率无关。证毕

（二）既有保留价又有佣金率

当展示广告的保留价r ＞0，且佣金率c ≠0时，先确定需求方满足的初始条件，即参与竞价与不

命题3当保留价r 和佣金率c 同时存在时，需求方的竞价策略为br(v ,r,c)，其中v*=(1+c)r，

证明 假设其它需求方都采用对称的竞价策略br(·)，而需求方i 的报价为br(z)，则i 得期望收益为

类似命题1中的计算过程可以得到

对（20）式从v*到v 积分可得

下面分别计算当保留价和佣金率都存在时,广告供给方、广告交易平台、广告需求方的期望收益。

广告供给方即广告展示平台的期望收益为

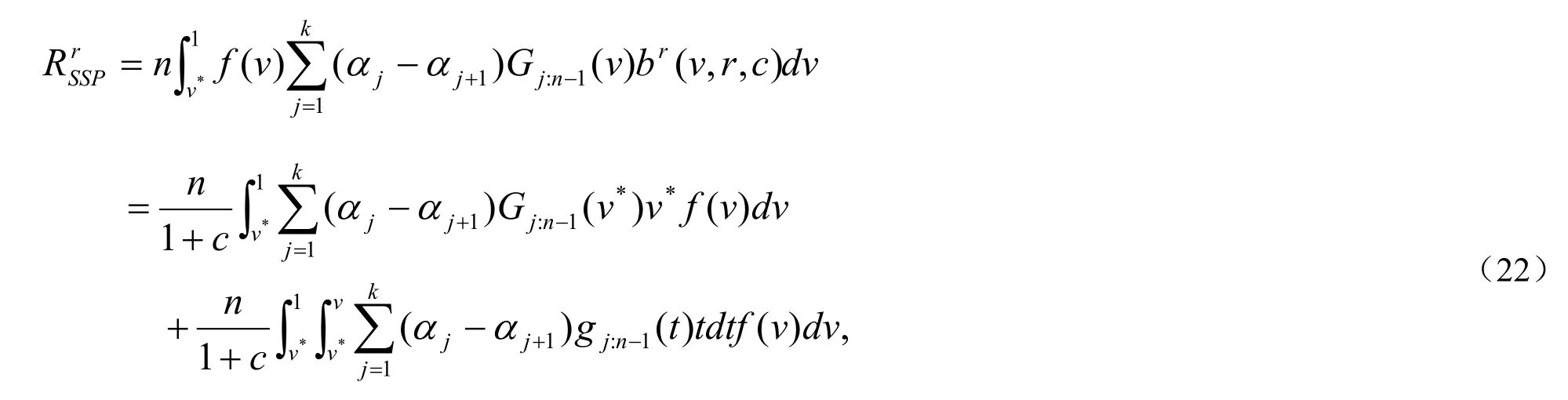
对上式第二部分交换积分顺序可得

对（24）式后半部分是用分部积分可得

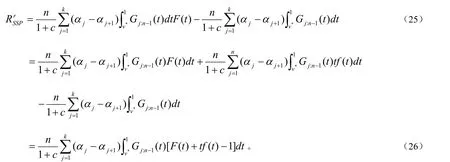
命题 4 假设广告展资源的保留价值为v0，如果佣金率c外生给定，则广告展示平台所确定的最优保留价满足如下条件

证明 由（26）式可以得出广告交易平台出售广告资源获得的期望收益，如果广告资源没有卖出（即所有的需求方的报价均低于保留价），那其获得期望收益为从而可以得到其总的期望收益为

对总的期望收益关于保留价r 求一阶条件

广告交易平台获得的期望收益为

命题5 假设保留价r 外生给定，则广告交易平台的最优佣金率满足

其中v*=(1+c)r，L(x)=F(x)+xf(x)-1。

证明 对广告交易平台的期望收益关于佣金率求一阶条件，由（29）可得

对上式整理可得（30）。证毕

命题6当保留价存在时（r＞0），需求方的期望支付关于佣金率递增，即当佣金率增加时需求方的期望支付增加。

由上式后半部分被积分函数大于零，当佣金率增大时必有v*增大，从而几分区间变小，所以后半部分的值变小所以期望支付增大。

四、结论

论文基于广义一价的支付方式,对实时竞价中的佣金率进行了研究。首先，本文给出了在固定佣金率以及线性佣金率时需求方（DSP）的报价策略，并且证明了在无保留价时，需求方的期望支出与任何形式的佣金率无关，佣金率只是改变了均衡的报价策略。其次，论文对既有保留价又有佣金率的情况进行阐述，指出在保留价存在时需求方的期望支出与佣金率相关，佣金率增加时需求方的期望支出增加[16]。即保留价存在时，需求方无通过调整自己的均衡报价来对冲佣金率的提高对自己的期望损失。最后，论文分别假定保留价和佣金率为外生给定，得出了最优佣金率和最优保留价满足的条件。