基于学科核心素养的“全等三角形”复习课设计

■杨文，陈开文

核心素养在全面深化课程改革，落实立德树人根本任务中具有重要作用和突出的地位，近年来，核心素养的培养已成为中小学课堂教学的指导思想和基本方向，如何在具体教育实践中让学科核心素养落地落实，这是广大教育工作者必须厘清的关键问题。笔者以一堂青年教师赛课——北师大版初中数学教材七年级下册第四章 “全等三角形的复习”为例，结合自身教学实践，谈谈怎样在初中数学复习课中将数学的核心知识、基本思想方法、数学精神等教育渗透到复习中[1]，从而真正做到有效提升学生的核心素养，为教师在数学复习课中落实核心素养培养提供一些借鉴。

一、教学过程

（一）课前准备，积累活动经验

落实学科核心素养的培养就是要组织、实施好学科活动。教者以活动为引领，在课前准备中为学生布置了一个前置活动：1.用硬纸片剪出两个等腰直角三角形；2.用两个等腰直角三角形，拼成自己喜欢的图形；3.上课时，请同学们来分享拼好的图形。

教学分析：由于活动要求并没有规定两个等腰直角三角形的大小，故应分类讨论：可以是两个一样大小的等腰直角三角形，也可以是一大一小的等腰直角三角形。通过“前置活动”的形式，不仅可以让同学们回顾等腰直角三角形的基本性质，还可以让学生动手裁剪、设计，最后拼接成一个美丽的图形，从中感受到数学的美。在课堂上，让同学们上讲台来展示自己的“作品”，并分享自己的设计方案和想法，还引出了本节复习课研究的所有基本图形。整节课同学们都在研究自己设计出的图形的性质，这大大激发了学生学习的积极性和主动性。以下是部分同学的拼图：

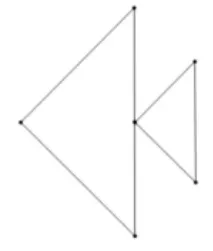
图1

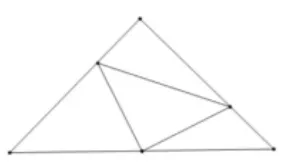
图2

图3

图4

（二）知识回顾，熟悉基本性质

落实学科核心素养就是要有过硬的学科基础知识。好的教学设计要着眼于学生的最近发展区，从学生已有的知识和经验出发，因此，教者在新课伊始，设计了两个与本节课相关的数学基础知识的问题：（1）如图5，已知ΔACE为等腰直角三角形，∠CAE=90°，AC=AE,请找出相等的角和线段。（2）如图6，已知ΔABD和ΔACE是等腰直角三角形，AB=AD，AC=AE，∠BAD=∠CAE=90°，请找出相等的角和线段；线段BD与CE有什么位置关系？

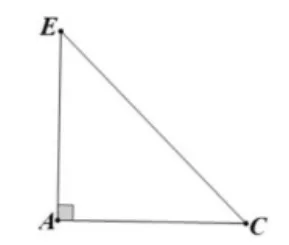
图5

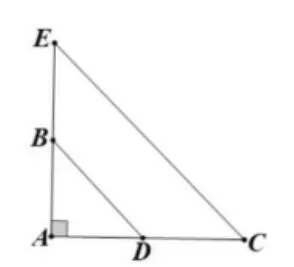
图6

教学分析：问题（1）根据等腰直角三角形的基本性质，可以知道底角相等、腰相等，有一个角是直角。这不仅可以帮助学生回顾等腰直角三角形的基本性质，还为后面的问题做铺垫。教者由一个简单的等腰直角三角形入手，让每个学生都可以参与进来，提高了学生学习的积极性。问题（2）中相等的线段有AB=AD，AE=AC，通过线段的比较可以得到BE=CD。其中相等的角有∠A=∠A=90°，∠E=∠C=∠ABD=∠ADB=45°,∠EBD=∠CDB=135°，根据平行线的判定可以知道线段BD与CE的位置关系为互相平行。随着图形变得复杂，不仅考查了学生运用等腰直角三角形的性质解决问题的能力，还考查了学生对基本模型的识别能力，进一步为后面的教学环节埋下伏笔。

（三）求同存异，回归图形本质

落实学科核心素养的关键是要抓住事物的本质。三角形全等的重点在于图形的变化较多，但究其本质就是两个三角形平移、旋转、对称等变换，因此，教者以旋转为抓手，引导学生从他们自己拼接成的图形入手研究问题（3）：如图7，已知ΔABD和ΔACE是等腰直角三角形，∠BAD=∠CAE=90°,AB=AD，AC=AE，连接CD，BE，试找出图形中的全等三角形；试探究BE与CD有什么关系。问题（4）：如图8，已知ΔABD和ΔACE是等腰直角三角形，∠BAD=∠CAE=90°，AB=AD，AC=AE，连接CD，BE，试找出图形中的全等三角形；试探究BE与CD有什么关系。问题（5）：如图9，已知ΔABD和ΔACE是等腰直角三角形，∠BAD=∠CAE=90°，AB=AD，AC=AE，连接CD，BE，试找出图形中的全等三角形；试探究BE与CD有什么关系。

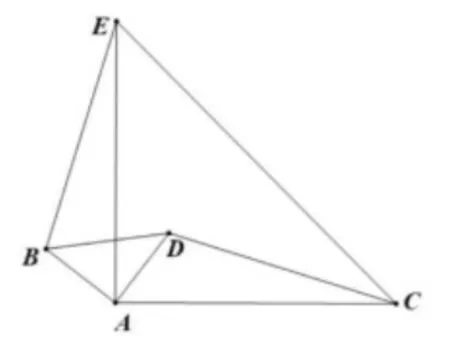
图7

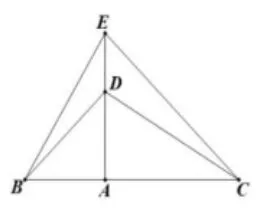
图8

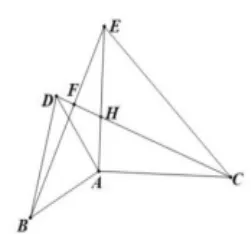
图9

教学分析：教者以旋转变换为切口，用三角形全等来研究旋转变换中的不变关系。根据旋转型全等这个基本模型，不难发现图7中全等的三角形为ΔABE和ΔADC。在全等的条件下，自然有BE=CD，本题的难点在于探究BE与CD的位置关系，值得注意的是在探究两线段之间的关系时，应分类讨论，其关系不仅包括位置关系，如平行、垂直等，还包括数量关系，即两线段相等的情况。在问题（3）和问题（4）中需要延长CD交BE于点F，根据转移角的基本模型“蝴蝶型”，以问题（4）为例，如图10，因为ΔABE≅ADC（SAS），所以∠FED=∠ACD,又因为对顶角，所以∠FDE=∠ADC,在ΔFDE与ΔADC中，三角形内角和均为180°，所以∠EFD=∠CAD=90°，所以BE⊥CD。本环节三个问题的已知条件基本一致，图形具有变化的连续性，揭示出了本节课研究的主题：在等腰三角形的问题中，通常涉及全等、旋转等元素，由于图形均由学生自己拼接而成，大大地激发了学生研究的兴趣。复习课的重点不仅是要教会学生识别复杂图形中的基本模型，更为关键的是教会学生研究基本模型变换的规律，抓住变换的本质，从而做到举一反三，知一通百。

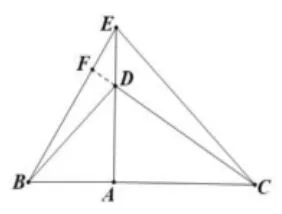
图10

（四）小组合作，培养创新能力

本节课的难点在于同学们能否在教师的引导下，通过小组合作在原来的基本模型中探究出其他结论。先独立思考，再小组讨论，最后请小组分享成果。问题（6）：如图11，已知ΔABD和ΔACE是等腰直角三角形，∠BAD=∠CAE=90°，AB=AD，AC=AE，连接CD，BE，连接AF，试说明∠BFA=∠CFA。问题（7）：如图12，已知ΔABD和ΔACE是等腰直角三角形，∠BAD=∠CAE=90°，AB=AD，AC=AE，连接DE，BC，过点A作BC的垂线交BC于点M，延长MA交DE于点N.试说明DN=EN。问题（8）：请同学们根据自己拼接的图形，类比本节课探究的模式，命制一道题并给出解答。

图11

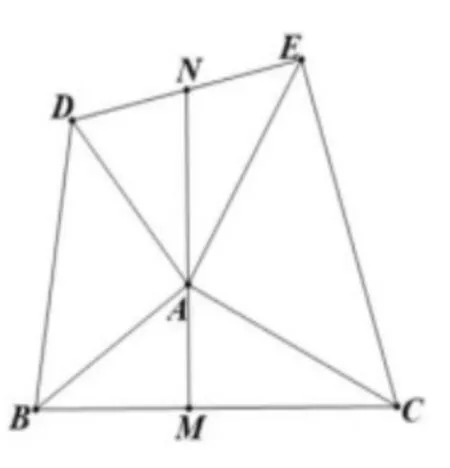
图12

教学分析：问题（6）要证明∠BFA=∠CFA，即证明AF平分∠BFC，根据角平分线的判定，过点A作AM⊥BE，AN⊥CD分别交BE，CD于点M，N，只要能够证明AN=AM即可，根据问题（5）可知ΔABE≅ADC（SAS），所以SΔABE=SΔADC且BE=CD，由等面积法可知三角形的高相等即AN=AM，所以AF 平分∠BFC，故∠BFA=∠CFA得证，本题涉及了全等的运用，角平分线的判定以及遇到角平分线应过角平分线上的点作角两边的垂线的基本模型。问题（7）考查了学生对“K”型全等的识别和运用，如图13，过点E，D，作EG⊥MN，DH⊥MN分别交MN于点G,H，因为∠EAC=90°，所以∠EAG+∠CAM=90°，又因为EG⊥MN，所以∠EAG+∠GEA=90°,所以∠GEA=∠CAM,又因为AE=AC,所以ΔAGE≅CMA （AAS），所以GE=AM；同理可得DH=AM，所以ΔDHN≅EGN（A AS ）,所以DN=EN。教者为了进一步深入挖掘题目中的价值，继续引导学生探究图形的本质，设置如下追问：若将DN=EN当作条件，其他条件不变，能否证明AM⊥BC？问题（8）是一个开放性问题，充分利用课前活动中拼接的图形，培养学生发现问题、提出问题、分析问题、解决问题的能力。本环节均是通过小组合作探究，围绕同学们拼接而成的图形，利用全等的基本模型继续深入探究图形的性质，挖掘图形的本质，让学生经历研究图形性质的过程，提升独立研究的能力。

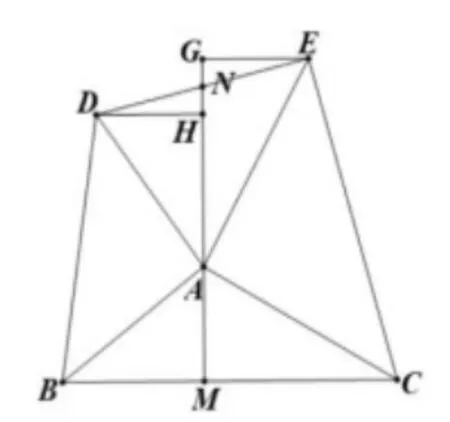
图13

二、教学反思

复习课是学生学习数学的重要组成部分,通过对所学内容的复习，可让学生进一步理解知识[2]，巩固已学过的知识、方法、思想，使其建立起系统的知识体系，发展学生的核心素养，也为新的学习内容做铺垫。

（一）在学科活动中培养核心素养

学科知识与学科活动是学科核心素养形成的两翼，学科知识是学科核心素养形成的主要载体，学科活动是学科核心素养形成的主要路径[3]。也就是说，核心素养的培养应该坚持杜威提倡的“做中学”，在学校学习过程中，则需要依托学科教育实践活动来实现。在平时的教学活动中，教师应合理设计活动，注重融入核心素养，以活动来引导学生动手操作，激发学生的探究兴趣，从而实现核心素养的有效培养。由此，提出两点建议：一是活动设计应具有明确、简洁、可操作性等特点；二是活动设计应紧贴复习课主题或生活情景。

（二）在问题探究中培养核心素养

无论我们采取何种方式方法设计落实核心素养的复习课，核心素养的落地都高度依赖问题情景，正是高质量的问题串设计[4]，才能有效沟通知识和素养之间的联系，借助于问题串可以帮助学生更好地巩固基础知识，提升学生使用数学方法分析问题和解决问题的能力，而且通过问题串的设计丰富了学生学习的进程，有助于学生核心素养的提升[5]。通俗地讲，复习课就是基于一个能够体现核心素养的核心问题，并将其分解为一个个问题串，引导学生在探究实践中一步步靠近复习课的最终问题的解决。由此，提出两点建议：一是问题串的设计要重视生活情景和知识情景的创设；二是问题串的设计要设置梯度，层层深入，把看似零散的概念、规律有机渗透在问题探究的全过程[6]，更要有意识地重视开放性问题的设计。

（三）在创新实践中培养核心素养

创新不是凭空臆造的，而是建立在知识的传播、转化和应用的基础之上的，无论是知识的创新还是技术的创新，都离不开教育[7]。教者在最后设置的问题（8）中，利用学生活动成果，模仿课堂图形探究流程，充分发挥他们的想象，让学生自己提出问题、分析问题，并解决问题，积累创新活动的经验，进而提升学生创新的意识。由此，提出三点建议：一是重视学科活动的设计； 二是发挥小组合作优势；三是精心设计问题串。

三、结语

促进学生数学核心素养的发展是初中数学复习课的重要方向，因此，复习不是简单的对新课期间所学的知识“炒冷饭”，也不是针对新课期间的难点反复地“机械刷题”，而是借助具有结构性的问题从更高的视角让学生联系地、整合地、本质地看待所学习过的内容[8]。基于核心素养的复习课教学需要教师更好地理解数学，创造性地设置活动，巧妙地设置问题串，坚持培养创新能力，切实将培养学生核心素养融入复习课的每一个教学环节中，实现学生的全面发展[9]。