基于MATLAB和Pro/E的非圆齿轮设计

宋威震，何 勇

(东华大学机械工程学院，上海 201620)

0 引言

非圆齿轮能够实现两轴间变速传动，是一种传动特性优越的变速机构[1]。由于非圆齿轮具有独特的优点，应用中往往需要非圆齿轮满足特定的传动比要求，用来完成特殊的函数关系[2]或者改善机械的运动。

非圆齿轮节曲线是非圆齿轮创新的关键，很多学者都在研究非圆齿轮的节曲线，并且提出了一些新式非圆齿轮[3]。非圆齿轮的设计中，其传动比是在节曲线确定后得到的，即利用非圆齿轮封闭且共轭的条件构造出节曲线，本文设计节曲线，用以实现特定的传动比函数。

有关非圆齿轮节曲线及传动比的分析，很多文献做了研究，贺敬良等[4]研究了变性椭圆齿轮机构，并做了速度的求解，但最后没有对其进行三维仿真。FIGLIOLINI等[5]设计了非圆齿轮，主要包括压力角、节曲线和凹凸性等，但没有建立非圆齿轮的三维模型。LIU等[6]进行了高阶非圆齿轮的设计，给出了具体的设计流程，但没有进行具体的实例分析。谢瑞雪等[7]研究了变性椭圆齿轮，使用MATLAB进行了实例分析，但最后没有进行三维仿真分析。刘炀等[8]做了变性椭圆齿轮的研究，并做了三维建模，但没有进行运动学研究。分析已有文献发现，非圆齿轮的设计大多基于二维软件，非圆齿轮的齿廓点提取过程繁琐而且时间较长，多数论文对非圆齿轮仅做仿真分析，未涉及到理论分析，造成设计结果不严谨。本文完整的呈现非圆齿轮设计过程，为其它文章提供一个参考作用。

求解非圆齿轮传动的首要工作是确定节曲线，主要分为3种方式[1]，即：给定传动比函数和中心距；给定再现函数和中心距；给定主动轮的节曲线方程和中心距。本文不选用上述传统方式，采用另外一种新的方式——只给非圆齿轮传动比函数，不给中心距。采用这种方式来设计，具有更大的范围性和更好的通用性。

已有论文提到的非圆齿轮设计过程和方法，比较繁琐而且不太严谨[12]，另外，对于设计的非圆齿轮不进行验证，设计结果不具有说服力。为了解决这些问题，本文提出一种非圆齿轮的设计方法，此方法设计非圆齿轮过程简单、通用性强、精度较高。论文整体步骤为：结合已知传动比条件，首先使用MATLAB求解非圆齿轮的中心距、节曲线和啮合位置，接着，运用包络法包络形成非圆齿轮齿廓，然后通过齿廓点的提取生成二维非圆齿轮，把生成的二维图形，导入Pro/E中，拉伸成三维模型，并把齿轮副进行装配，最后把装配的图形导入到Adams中，完成动力学分析，求齿轮副角速度曲线。同时为了结果的严谨性，对非圆齿轮副进行了理论分析，并与运动学仿真进行对比。

1 非圆齿轮基础理论

1.1 非圆齿轮传动比

非圆齿轮传动比是以主动轮转角为自变量的周期函数，它表示主从动齿轮的速度变化关系。以外啮合齿轮副为例，设给定的传动比为i12(φ1)=f(φ1)，由运动规律可以推导得出：

(1)

式中，ω1为主动轮角速度；ω2为从动轮角速度。

从动轮位置函数φ2(φ1)是φ1的函数，从动轮节曲线封闭要求当主动轮旋转一周时，从动轮是一个封闭的齿轮，须符合φ2(2π)=2π×n或φ2(2π)=2π/n，其中n为整数。

从动轮位置函数计算公式为:

(2)

1.2 节曲线方程

设中心距为a，主动轮的转角为φ1，传动比表达式i12=f(φ1)，则主动齿轮节曲线计算公式:

(3)

从动齿轮节曲线r2(φ1)和转角φ2计算公式为:

(4)

(5)

1.3 非圆齿轮中心距

因为主从动轮能够实现整周旋转，运动过程可以看成主从动轮节曲线在做纯滚动。设主动轮的齿数为z，模数为m，则弧长为:

(6)

设r1a=r1/a，根据式(6)可得主从动轮安装中心距a的计算公式如下：

(7)

2 实例分析与求解

本文实例分析：要实现的传动比i12的方程如下:

i12(φ1)=1.118+0.5sin(φ1)

(8)

式中，传动比函数是以主动轮的转角φ1为自变量的函数，本文假设主动轮模数m为2.5 mm，齿数z为19。

因为非圆齿轮设计的过程中需要考虑多种因素，比如是否根切、节曲线是否封闭和凸凹性检验等，参照文献[7]，本文给出非圆齿轮设计的过程图，以便更清楚表达本文求解非圆齿轮过程，如图1所示。

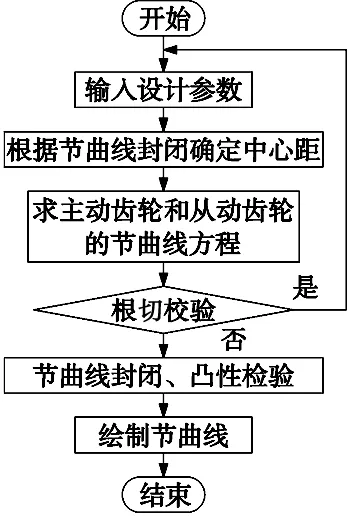
图1 程序流程图

下面根据流程图进行非圆齿轮的求解，首先确定主从动轮的中心距，由式(3)、式(7)、式(8)可求得主从动轮安装中心距:

(9)

所以，可以求得主从动齿轮安装中心距a=48.17 mm。因为非圆齿轮的中心距已经求出，联立式(3)、式(6)、式(9)可以求出主动轮节曲线的弧长，由弧积分公式可得:

(10)

因此，可以求得主动齿轮的弧长为149.2 mm。

2.1 根切校验

因为非圆齿轮节曲线的曲率半径是变化的，在加工过程中也许会造成根切，所以有必要验证是否根切，不发生根切为:

(11)

2.2 封闭性检验

下面进行从动轮的封闭性检验，根据从动轮的位置函数，由式(5)、式(8)可得：

(12)

对该函数进行计算，当φ1=2π时，φ2(2π)=2π，即主动轮转过一圏，从动轮转过一圈，符合节曲线封闭的要求。

2.3 凹凸性检验

在加工非圆齿轮前，必须预先知道节曲线的凹凸性，所以进行凹凸性计算，具体参照文献[1]。

主动轮节曲线不出现凹形的条件为:

(13)

从动轮节曲线不出现凹形的条件为:

(14)

经检验后，主从动轮节曲线都是外凸。

2.4 主从动齿轮节曲线

已知式(8)的传动比函数，联立式(3)、式(8)可以推出主动齿轮节曲线为:

(15)

根据式(4)、式(8)可以求解从动齿轮节曲线为:

(16)

根据式(15)、式(16)计算结果，然后根据式(9)计算出来的中心距，使用MATLAB可求得主从动轮的节曲线。

2.5 非圆齿轮的回转中心

下面求非圆齿轮的回转中心(焦点)，当前，国内外学者对非圆齿轮回转中心的研究，一般都是关于椭圆齿轮，有关其他类型的非圆齿轮回转中心的研究目前鲜有介绍，本文依据椭圆齿轮的有关结论，对非圆齿轮的回转中心进行求解。根据主从动轮节曲线和中心距可求得非圆齿轮的啮合位置，得出图2。下面求主动轮的回转中心，从动轮的数据可以参考主动轮的计算过程。根据式(15)画出主动轮节曲线，可以求出非圆齿轮的“长轴”为48.17 mm，如图2所示中主动轮的粗线所示，“短轴”为46.82 mm，如蓝色线所示，最后可以求得“焦距”为5.67 mm，如图中O1—C1所示，C1即啮合传动时主动轮的回转中心。同理，可以求得从动轮的焦距O2—C2，从动轮的回转中心为C2。下面进行非圆齿轮回转中心正确性的验证，以主从动轮的相切点为初始点，在主从动轮上按照相同长度的弧长，找6个点，模拟非圆齿轮纯滚动运动，非圆齿轮中心距分别为C1—1和C2—1的和、C1—2和C2—2，以此类推。求解得知：6个数据点的和都十分接近中心距48.17 mm，证明本节求出的回转中心正确。

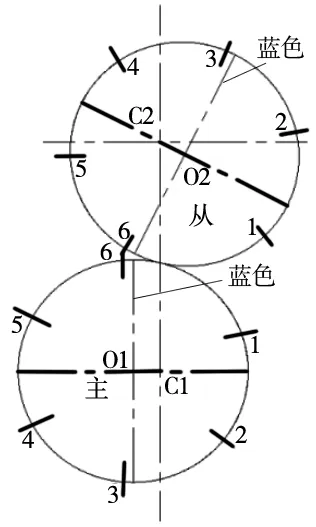
图2 非圆齿轮节曲线和回转中心

3 非圆齿轮建模

3.1 非圆齿轮齿廓的绘制

目前对非圆齿轮的求解多采用包络法[9]和齿形折算法，但是齿形折算法精度低，过程复杂，所以用的越来越少，所有本文使用包络法进行非圆齿轮的设计，这种算法理论已经非常成熟，故这里不再详述。借鉴其他文献[10]，标准渐开线齿廓的插齿刀具包络形成非圆齿轮齿廓，根据式(15)，包络生成的主动轮齿廓如图3所示。同理可以生成从动轮齿廓，这里不再显示。使用图像处理的方法[11]，可以快速提取齿廓点，把齿廓点数据导入到Autocad中可得到非圆齿轮图形，如图4所示。为了更好地表示两个非圆齿轮的位置和啮合情况，结合图2求得的非圆齿轮的回转中心，画出主动齿轮和从动齿轮的啮合图。

图3 插齿刀具包络非圆齿轮齿廓 图4 主动齿轮图形

3.2 非圆齿轮装配

把得到的非圆齿轮的二维图形导入到Pro/E中，利用拉伸命令，拉伸厚度为40 mm，拉伸以后得到非圆齿轮三维模型，在图2中得到的回转中心位置处设置一个直径为6 mm的孔洞作为安装位置，在Pro/E软件中进行装配和设置约束，以主动轮和从动轮的安装中心点设置齿轮转动命令，装配后如图5所示。

图5 非圆齿轮三维装配图

把主动轮回转中心处设置电机进行转动，这时，从动轮会跟着主动轮进行相应转动，观察发现，齿轮副在转动过程中啮合良好，转动平稳，达到齿轮转动要求。

4 非圆齿轮运动学分析

利用Adams软件，对非圆齿轮进行运动学分析，验证非圆齿轮转动时输出的传动比与理论传动比是否一致。运动学分析能够使设计的产品进行及时的验证和分析，这种验证不需要大量的人力和金钱，可以很容易的获得结果，最主要的是可以减少产品的研发时间。

在Adams中定义材料的刚度是20 000 N/mm，力指数是2.2，最大阻尼是400 N·s/mm，在运动学过程中允许接触在小距离内的相互渗透。在主从动轮的回转中心设置为转动副，接着在主动轮的回转中心设置旋转驱动，如图6所示。旋转副驱动为30 °/s，运动的时间为32 s，步数为320步，然后开始进行运动学分析，根据齿轮副的运动，得到主动轮的角速度曲线如图7所示，从动轮的角速度曲线如图8所示。

图6 非圆齿轮在Adams中的装配图

图7 主动轮角速度图

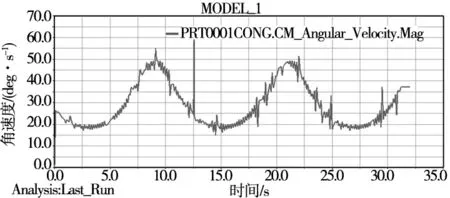
图8 从动轮角速度图

在非圆齿轮转动时两齿轮啮合良好，满足共轭齿轮传动要求，证明了设计的非圆齿轮是正确的。由图7可以看出，在Adams运动仿真中，主动轮角速度图为一条直线，即主动轮为匀速转动。图8曲线不光滑的原因可能是：由于非圆齿轮相对复杂，而且轮齿数量较多，导致其累积误差更大，仿真曲线有地方发生失真现象。

5 非圆齿轮理论分析

把得到的主动轮和从动轮啮合图进行每个齿的分析，给每个齿编号，如图9所示，分别测量主动轮和从动轮的回转中心到每个齿的距离，从动轮角速度[1]为ω2=ω1/i12，结果如表1所示。主动轮的角速度与本文第4节相同，为30 °/s，这里为了表格简洁，仅列出了部分齿的数据,注：这里主动轮角速度和从动轮角速度单位都为°/s。把表1中的传动比和从动轮角速度与从动轮齿的对应关系进行画图，结果如图10、图11所示。

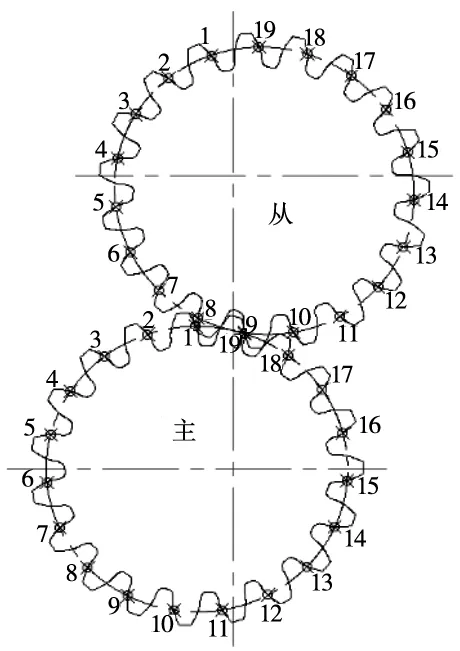
图9 非圆齿轮传动的运动特性

表1 非圆齿轮理论数据求解

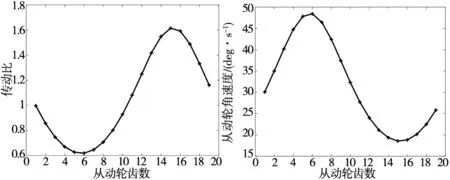
图10 非圆齿轮传动比 图11 从动轮角速度

观察图10可以看出，把非圆齿轮的理论传动比与要实现的传动比i12(φ1)=1.118+0.5sin(φ1)进行对比，发现图形基本一致 。观察图11和图8可以得出，从动轮的理论角速度与Adams仿真得出的从动轮角速度曲线基本一致。通过对图10和图11进行分析，很好的证明本文设计非圆齿轮方法的正确性。

6 结论

针对非圆齿轮设计过程繁琐，齿廓特征点提取时间长，提出一种简单的非圆齿轮设计方法，通过一个数值算例进行分析，证明方法的正确性。结果表明，从动轮的角速度曲线和理论传动比曲线极其接近，证明了本文方法的正确性。因此,只要给出了主从动轮传动比函数，即使不给出中心距，也可以计算出非圆齿轮齿廓，使非圆齿轮设计更具有普遍性和通用性。对非圆齿轮回转中心进行精确求解并验证其正确性，使求解更加严谨。以MATLAB和Pro/E为工具，生成非圆齿轮三维模型，比传统CAD软件绘制非圆齿轮更加简单

快捷，提高了设计的效率和精度。本文提出的方法相比其他文献的非圆齿轮设计方法更加简单省时，复现性强。