列车晚点下高速铁路车站到发线运用计划调整方法

廉志斌 ，帅 斌 ，许旻昊

（1.西南交通大学 交通运输与物流学院，四川 成都 611756；2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 611756；3.西南交通大学 综合交通大数据应用技术国家工程实验室，四川 成都 611756)

0 引言

高速铁路列车在运行过程中可能因灾害天气、设备故障等因素而发生晚点，前行列车晚点或将导致后行列车的连带晚点。列车晚点发生后，原定的列车到发线运用计划很可能存在冲突，如果按原定计划安排列车的接发车作业，很可能会降低局部路网的运输效率。此时，列车调度员可以调整列车的到发线运用计划，疏解列车到发线运用冲突，从而减少列车的晚点。

在关于列车到发线运用计划调整的研究中，Chakroborty 等[1]假定车站在列车到达车站前60 min得知其晚点时长，以列车延误成本、列车变更到发线造成不便的费用最小化为目标，构建混合整数规划模型。Jánošíková 等[2]将出发列车延误时间最小和乘客不便最小作为目标，构建到发线调整模型。在此基础上，Jánošíková 等[3]以最小化到达和出发晚点时间、最大化列车占用到发线的可取性为目标，构建混合整数规划模型。Zeng 等[4]根据混合整数线性规划和车站调度理论，分别针对正常情况和晚点情况构建多准则车站进路选择模型。王韩冬[5]通过建立两阶段规划模型，首先为车站到发线赋予不同的权重，然后求解列车晚点最小和列车变更到发线数目最少的到发线运用计划。乔瑞军[6]以列车在站内走行时间最小、到发线均衡使用为目标，建立到发线调整的多目标优化模型。朱昌锋[7]将列车实际出发时刻与图定时刻差值最小、列车实际占用股道偏离原计划程度最小为目标，构建到发线调整模型。刘伟[8]通过对列车赋权，进而构造列车进路选择和到发线调整模型。邓远冬[9]通过累积流变量刻画列车占用咽喉区进路与到发线的过程，建立考虑列车权重的高速铁路车站到发线运用计划调整0-1 整数规划模型，利用拉格朗日松弛算法求解。这些研究中，到发线调整的目标和列车权重的设置比较简单，且只考虑单侧车场作业，没有考虑上、下行车场的股道灵活运用，导致车站到发线运用计划与实际情况偏差较大。为此，以所有列车的连带晚点时间之和最少、所有列车实际占用到发线偏离原计划程度最小为目标，构建列车晚点下高速铁路车站到发线运用计划调整模型。该模型综合考虑了列车等级、作业类型及初始晚点时间3 类属性，提出更合理的晚点下列车权重设置方法，可以提升车站到发线运用计划的编制质量。

1 高速铁路车站到发线运用计划调整问题

1.1 问题描述

正常情况下，高速铁路车站按照图定时刻接发列车，并按原计划为列车安排到发线，而当列车发生晚点时，如果列车作业之间的缓冲时间无法完全吸收晚点，车站原到发线运用计划有可能存在冲突，需要调整原到发线运用计划，以减少连带晚点等负面情况。例如，某车站设有6 条到发线，其中2 条正线，车站平面布置如图1 所示。该车站接发A，B，C 方向的列车。列车原始到发时刻表及占用到发线信息如表1 所示。

表1 列车原始到发时刻表及占用到发线信息Tab.1 Original train arrival and departure timetable and information of occupied arrival and departure tracks

图1 车站平面布置图Fig.1 Layout plan of station

如果D4 次列车晚点9 min，最早到达时刻为11 :23，停在6 道。而D6 次列车原计划11 :24 到达且停放在6 道，因而需要为D6 次列车分配其他空闲到发线或使其晚点直至6 道空闲再将其接入。

到发线运用计划调整的目的是尽快为存在时间冲突的列车分配无冲突的空间资源。列车晚点下高速铁路车站到发线运用计划调整问题，是在已知列车晚点的条件下，考虑到发线、进路冲突等因素，通过优化列车的到发线分配计划，使所有列车的连带晚点时间和列车实际占用到发线偏离原计划程度最小。

1.2 列车潜在冲突判断

为了判断列车间的时间冲突，可事先计算出列车在车站可能停留的时间范围[10]，基于此可以分析得到所有可能存在冲突的列车对，既保证不会遗漏列车之间的冲突，又不必检查任意两列车之间是否存在冲突，提升求解效率。当车站某时间段发生列车晚点时，仍可以根据列车运行图及追踪列车最小间隔时间得出该时间段内每列车最早到站时间，然后根据每列车在站的进路走行时间和停留时间，可以得出每列车占用车站空间资源的时间跨度。以上小型晚点场景可以得到晚点后的列车冲突识别图[10]如图2 所示。

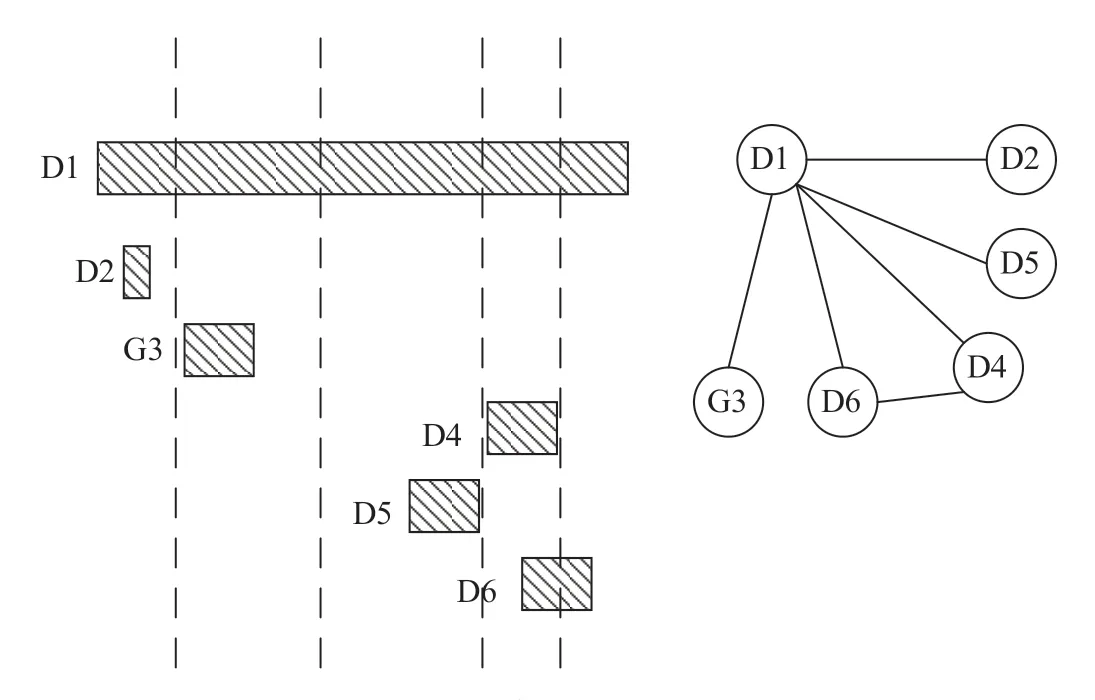
图2 列车冲突识别图Fig.2 Train conflict recognition diagram

由图2 可知，左侧的矩形长度分别代表D1—D6 列车占用车站空间资源的时间范围，在时间轴上存在时间重叠的两列车有可能发生冲突。将列车看作无向图的节点，并将可能存在冲突的列车对用边连接，得到表示列车冲突的识别图。根据列车冲突识别图可以构造列车冲突识别邻接矩阵如下。

矩阵Cn×n中的元素可表示2 列车之间是否可能存在冲突，可减少冗余的约束条件检验，提高求解效率。例如，元素c21=1 表示D2 次列车与D1 次列车可能存在冲突；c32=0 表示D2 次列车与G3 次列车不可能冲突。

1.3 晚点下列车权重设置方法

晚点情况下，列车的权重主要受到初始晚点时间、列车等级(如高速动车组旅客列车等级高于动车组旅客列车)和列车作业类型3 方面的影响。关于列车作业类型，采用贾文峥等[10]中的方法，根据列车作业类型设置权重规则如表2 所示。由于跨线列车的晚点会传播至其他线路，因而跨线列车的权重值需要在上述基础上加2。根据列车等级设置权重规则如表3 所示。采用min-max 方法分别对以上3 项指标进行归一化处理，计算公式为

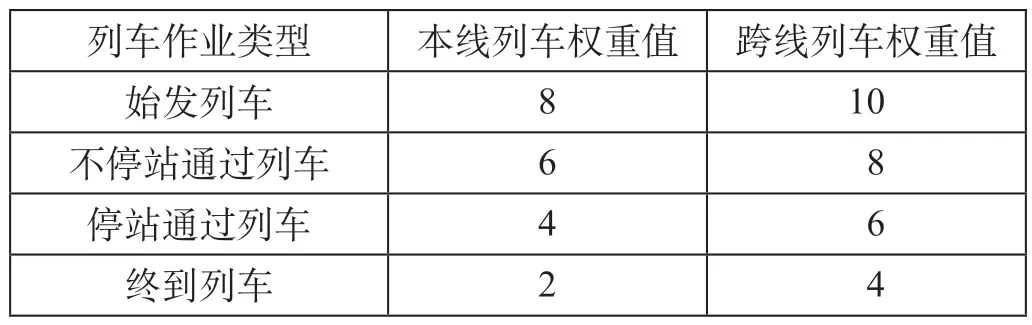
表2 根据列车作业类型设置权重规则Tab.2 Weighting rules setting based on train operation type

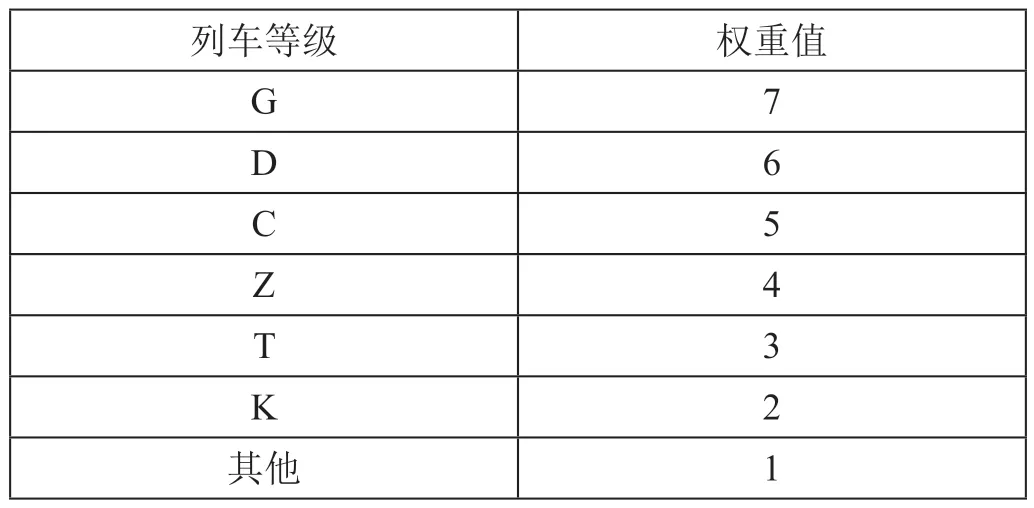
表3 根据列车等级设置权重规则Tab.3 Weighting rules setting according to train class

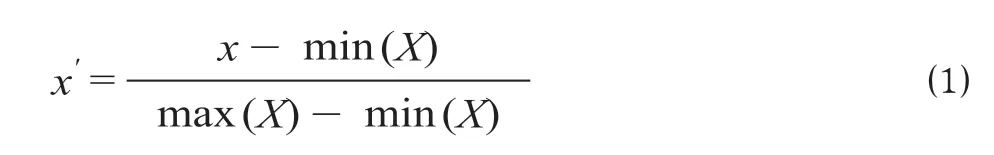
式中：x′表示个体归一化后的指标值；x表示个体归一化之前的数值；X表示一组同类型样本数据；min (X)表示X中最小值；max (X)表示X中最大值。

计算得到晚点条件下列车权重为

1.4 列车晚点下高速铁路车站到发线运用计划调整模型

设高速铁路车站在某时段内接发的列车总数为m；列车集合TR=[TRi]，i∈N+，i≤m。车站设有n条到发线，设车站到发线集合D=[Dj]，j∈N+，j≤n。设车站进路集合为J=[Jj]，j∈N+，j≤l。

模型有2 个目标函数，目标函数M1为所有列车的连带晚点时间之和最小，计算公式为

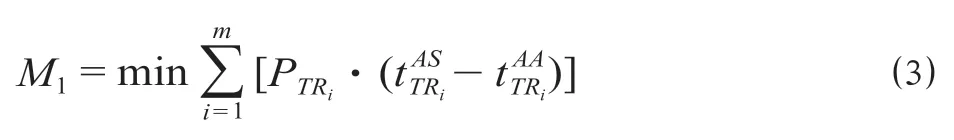
目标函数M2为所有列车实际占用到发线偏离原计划程度最小。既有文献多通过设置到发线惩罚值的方法描述，较为复杂且不够直观。为此，将车站的到发线从一侧开始由小到大编号(如图1 所示)。考虑到列车发生晚点时，车站工作人员会尽可能安排列车占用原计划到发线，如果必须变更到发线，则应尽可能选择距离原计划到发线较近的到发线，以减少旅客在候车大厅的走行距离，避免大批旅客更换检票口造成的拥堵，计算公式为

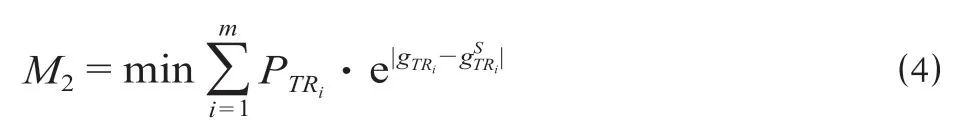
采用线性加权的方式整合目标M1和M2，得到总目标函数的计算公式为

式中：α和β分别为目标M1和M2的权重，用于权衡2 个目标的重要程度。

模型包括以下约束条件。

（1）到站时刻约束。晚点发生后，列车实际到达时刻不得早于列车最早到达时刻。

（2）出发时刻约束。列车实际出发时刻不得早于图定出发时刻。

（3）到发线唯一占用约束。设占用到发线时间存在冲突的列车所构成的集合为对于任意列车对于某一条到发线，存在到发线占用时间冲突关系的列车集合中，至多有1 列车可以占用此到发线。

（4）通过列车只能占用正线。

式中：TRXB表示下行不停站通过列车集合，TR；TRSB表示上行不停站通过列车；DXZ表示下行正线集合表示上行正线集合，。

（5）进路唯一占用约束。设占用进路时间存在冲突的列车所构成的集合为潜在列车——进路冲突集合，对于任意列车同一时间同一条进路至多被一列车占用。

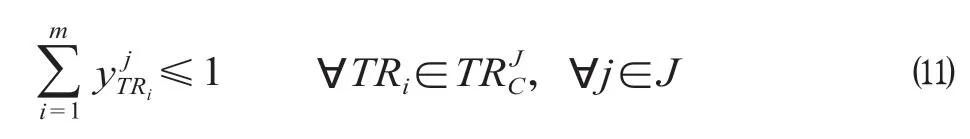
（6）占用进路时间存在冲突的列车不能同时占用敌对进路。对于任意列车不能同时占用敌对进路。

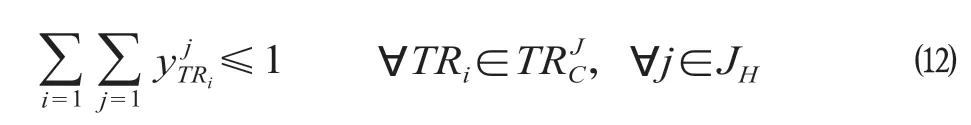
式中：JH表示某个敌对进路集合。

（7）到发线最小作业时间间隔约束。同一到发线上相邻进行作业的两列车的时间间隔需要满足最小安全间隔时间要求。

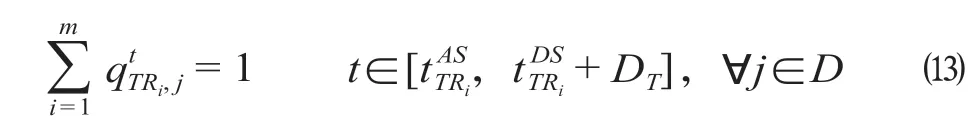
式中：DT表示到发线最小作业时间间隔；如果则t时刻列车TRi占用到发线j，如果0 则t时刻列车TRi未占用到发线j。

2 到发线运用计划调整模型求解算法

到发线运用计划调整问题属于大规模组合优化问题，属于NP-hard 问题。目前求解这类问题一般采用智能算法。考虑到遗传算法具有良好的全局搜索能力，可以快速地进行解空间的全局搜索。此外，列车占用到发线的决策变量属于0-1 变量，可以利用遗传算法中的交叉和变异算法实现解空间的搜索，因而采用遗传算法求解模型。遗传算法求解模型的步骤如下。

步骤1：设置初始参数。首先设置列车权重的3 项参数，然后设置目标函数中α和β。设置遗传算法初始参数：种群大小N值，迭代代数NP，算法停止条件参数NP_S，变异概率pm。

步骤2：编码。假设高速铁路车站在某时间段内存在m列车，以每列车占用到发线编号和连带晚点时间为基础，将种群中每个个体编码为1×2m的行向量，前m列代表m列车分别占用到发线的编号，后m列代表m列车各自的连带晚点时间。

步骤3：适应度函数值计算。遗传算法的适应度函数值即为目标函数值。

步骤4：约束条件检验。对种群中每个个体进行模型约束条件检验，并记录其是否为可行解。

步骤5：选择，交叉、变异。算法选择，交叉、变异规则如下：选择当前种群中目标函数值最大的个体La(Largest)及第二大的个体S-la(Second Largest)，对二者前m列的列车占用到发线信息进行交叉；选择目标函数值最大的个体La，根据变异概率，再随机对同一条线路上追踪运行的列车的连带晚点时间同时进行变异。

步骤6：判断是否满足终止条件。根据算法停止条件参数NP_S，若连续NP_S代的可行解中最小目标函数值无变化，则算法停止，或迭代至NP代，算法停止。

步骤7：得到满意解。程序循环至满足终止条件，算法结束，得到满意解。

3 案例分析

以图1 所示的高速铁路车站为例进行案例分析。该站设有2 个站台，6 条到发线(其中的2 条为正线)。以某日11 :00—12 :00 为案例分析时段。列车基本信息及原始时刻表如表4 所示。其中，D1 次列车为本线折返列车，D2，G7 和G12 次列车为不停站通过列车，其他列车为停站通过列车。

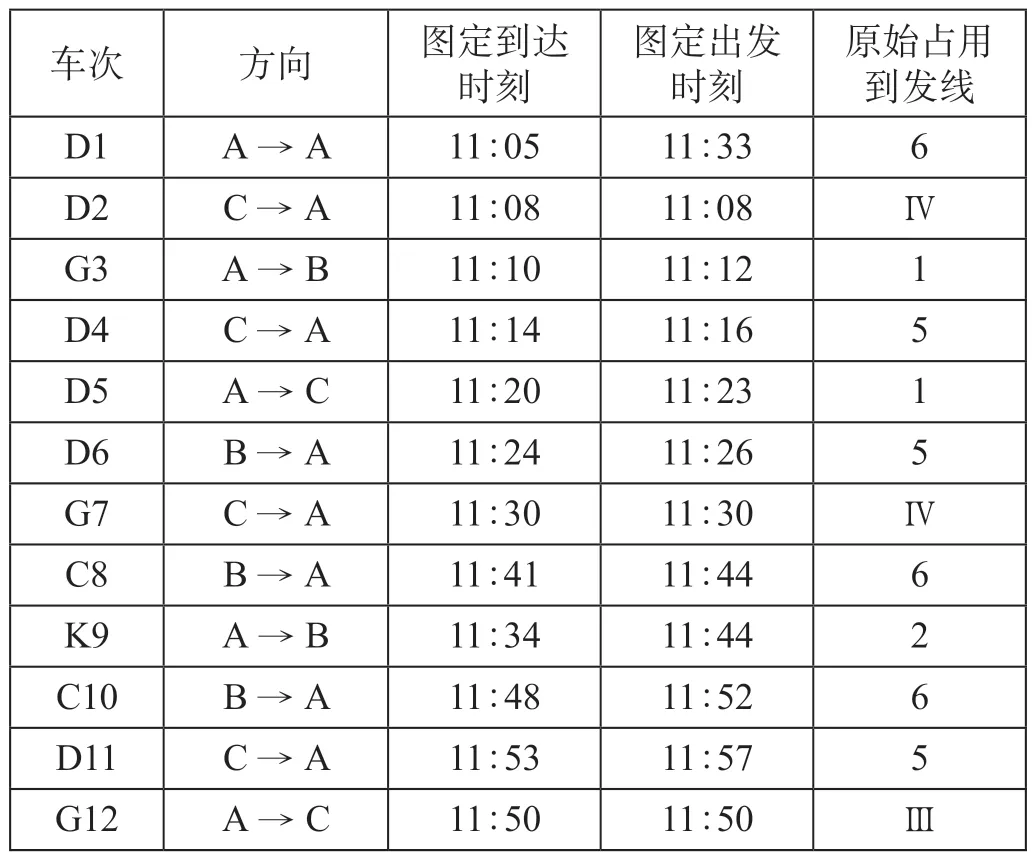
表4 列车基本信息及原始时刻表Tab.4 Original train arrival and departure timetable and basic information

案例假设D2 次列车晚点10 min，G3 次列车晚点10 min。在不考虑分段解锁的情况下，车站各项作业时间标准为：追踪间隔时间取4 min；停站通过列车接车进路开始时刻为到达时间前4 min，终止时刻为到达时间；停站通过列车发车进路开始时刻为列车发车前30 s，终止时刻为列车出发后3 min。不停站通过列车接车进路开始时刻为到达前2 min，发车进路终止时刻为到达后1.5 min。到发线最小安全间隔时间DT为5 min。

基于以上基础数据，利用上述模型和算法求解。其中，初始参数设置为：目标函数中α和β值分别设为0.7 和0.3，设置列车权重的系数λ1，λ2，λ3分别设为0.2，0.3，0.5。遗传算法种群大小N取60，迭代代数NP取1 000，算法停止条件参数NP_S取200，变异概率pm取0.85。遗传算法一般将变异概率设置为小于0.1 的数值，但由于编码的特殊性，将初始种群中的列车连带晚点时间设置为较大的数值，而变异的目的之一是不断减小列车的连带晚点时间。因此，为了快速减少列车连带晚点时间，找出满意解，将变异概率设置为较大的数值。

通过求解得到晚点后列车到发时刻及到发线调整信息如表5 所示。对比表4 和表5 可知，晚点发生后，模型求解得到的满意解中，有10 列车发生晚点，8 列车未占用原计划到发线。对此结果进行分析可知：D4 次列车和D5 次列车晚点的原因是与前方晚点列车追踪运行；D6 次列车、K9 次列车和D11 次列车晚点原因是到发线冲突；G7 次列车、C10 次列车和G12 次列车晚点原因是进路冲突；而D1次列车和C8次列车未发生晚点。

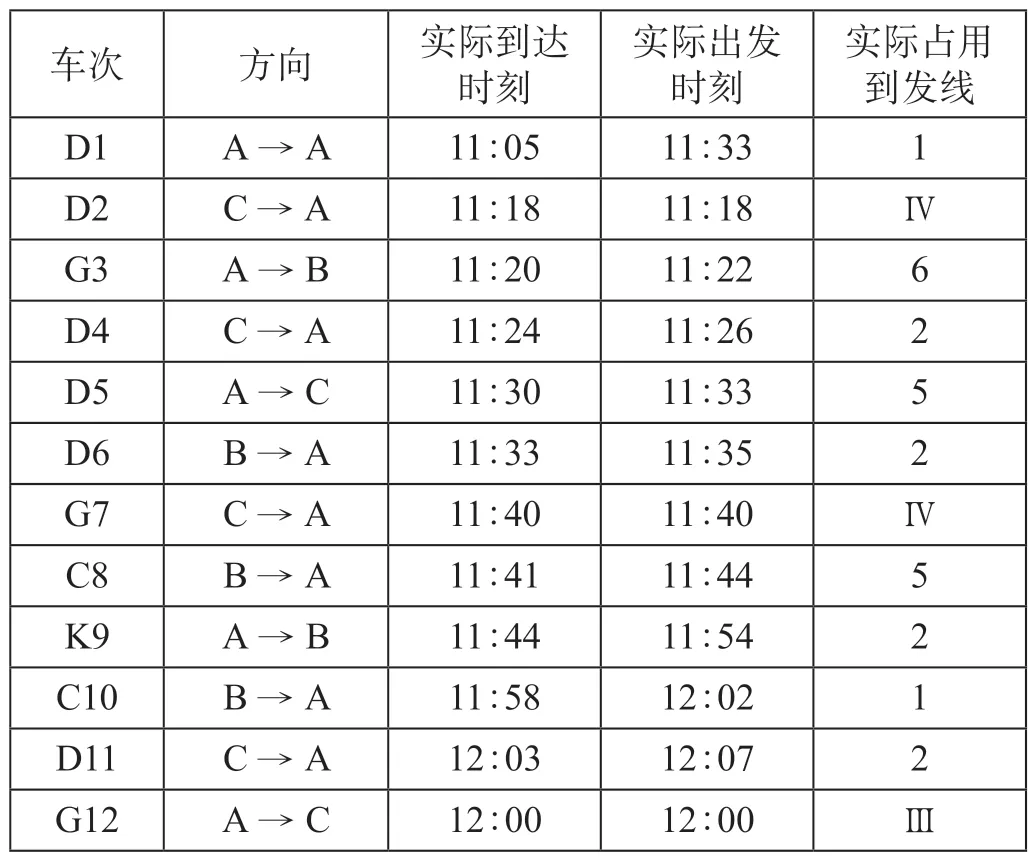
表5 晚点后列车到发时刻及到发线调整信息Tab.5 Train arrival and departure time and adjustment information of arrival and departure tracks after delay

遗传算法所得所有可行解的散点图如图3 所示，“最优”可行解与“最差”可行解如图4 所示。

图3 可行解的散点图Fig.3 Scatter plot of feasible solutions

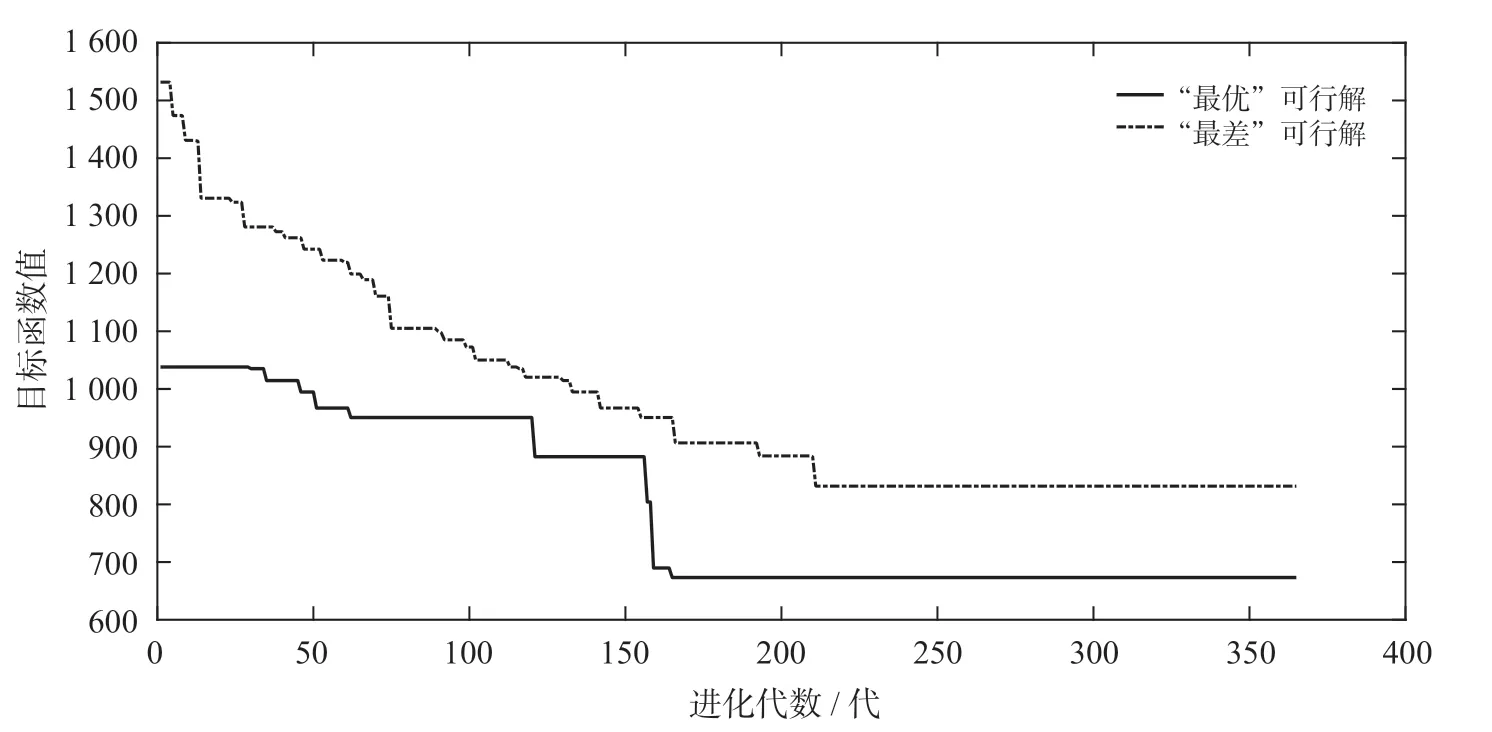
图4 “最优”可行解与“最差”可行解Fig.4 “Optimal” feasible solution and “worst” feasible solution

以上求解结果为α取0.7 时得到的满意解。基于以上案例，在α不同取值的情况下分别进行计算，以比较目标函数中两部分优化目标的重要程度。α不同取值下“最优”满意解到发线偏离原计划列车数、列车总连带晚点时间变化如图5 所示。

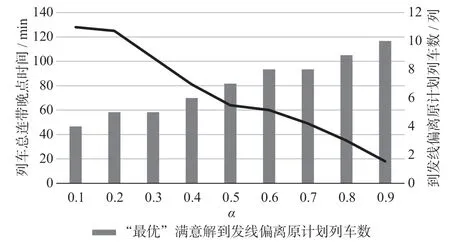
图5 α 不同取值下“最优”满意解到发线偏离原计划列车数、列车总连带晚点时间变化Fig.5 Changes in the number of trains on arrival and departure tracks deviating from the original plan and the total delay time of the “optimal”satisfactory solution under different α values

由图5 可知，随着α取值不断增加，算法所得“最优”满意解到发线偏离原计划列车数呈上升趋势，而“最优”满意解的列车总连带晚点时间呈下降趋势。这是因为α作为目标函数中列车连带晚点时间的线性相关系数，其侧重于寻找列车连带晚点时间更小的解，因而随着α取值不断增加，列车总连带晚点时间呈下降趋势。相反，“最优”满意解的到发线偏离原计划列车数呈上升趋势。在上述案例中，如果从降低车站工作组织紊乱程度的角度出发，可将目标函数中α设置为较小数值；如果从减少旅客候车时间的角度出发，可将α设置为较大数值。

4 结束语

针对列车晚点下高速铁路车站到发线运用计划调整问题，构造到发线运用计划调整模型，设计遗传算法求解，并通过案例计算验证模型的有效性。在到发线运用计划调整模型中，基于列车初始晚点时间、列车等级、列车作业类型3 种属性为晚点列车赋予权重，以所有列车的连带晚点时间之和最少、所有列车实际占用到发线偏离原计划程度最小为优化目标，并采取线性加权的方式对2 部分目标进行整合，在案例中为2 部分目标的权重系数赋予不同的取值组合，通过计算结果分析2 部分目标的重要程度与权重系数取值的关系，表明到发线运用计划调整的模型和算法可以减轻由于晚点导致的车站作业成本增加，有效遏制列车晚点在路网中的蔓延趋势，保证旅客服务质量。