基于TSP 问题思想的城市轨道交通乘务排班计划研究

苏 铭，刘兰芬，杨信丰，焦正玉

（兰州交通大学 交通运输学院，甘肃 兰州 730070)

0 引言

乘务排班计划是城市轨道交通乘务计划编制过程中的核心环节，即将运行图中的运行任务分解后组合成乘务工作班。我国城市轨道交通运营在管理制度、乘务制度、运输组织模式等方面均有独特性，且排班计划编制涉及的影响因素众多，求解难度较大，属于多项式复杂程度的非确定性问题。合理设计乘务排班计划，为司机安排适合的工作与休息时间，对于提高运营企业运输组织效率、服务水平与安全性具有重要意义。

城市轨道交通运行交路短，发车间隔密度大，线路和运营条件具有一定限制，都增加了计划编制的难度，故合理高效的乘务计划编制方法一直是城市轨道交通领域研究探索的重点。通常排班模型有集合覆盖与分割模型、基于值乘区段接续关系模型、网络图模型等，求解算法主要包括解析算法和智能算法。在铁路运输研究中，褚飞跃等[1]建立以集合分割模型为基础的双目标排班模型；林枫等[2]以乘务交路总接续费用和过夜费用最小为目标，设计改进的蚁群优化算法；Neufeld 等[3]建立混合整数规划模型，采用遗传算法与混合列生成算法求解。在城市轨道交通研究中，王莹等[4-5]构建集合覆盖形式模型，将列生成嵌入分支定价算法进行求解；张增勇等[6]建立双层规划排班模型，设计改进迪杰斯特拉算法和离散粒子群算法进行计算；李献忠等[7]运用分解模型，分2 步运用最短路和最小费用最大流算法进行求解；丰富[8]建立以时间均衡度为目标排班模型；Chu、袁仁杰等[9-10]设计改进遗传算法；金华[11]建立多层网络图模型，许仲豪[12]等建立集合划分模型，设计列生成算法求解；刘中举[13]以司机数量最小及作业效率最高为目标构建优化模型，结合树枚举和贪心算法求解；潘寒川等[14]以任务均衡为目标，研究“随乘”模式(DHM)与“虚拟班”模式(VGM)乘务计划编制方法。Janacek，Moreno 等[15-16]分别将列生成算法、分支定界算法应用于航空乘务排班、道路乘务排班与路径问题。国内研究主要侧重于乘务制度优缺点分析以及排班模型的构建，国外主要侧重于模型的求解算法，因城市轨道交通实际运营中的乘务规则、限制条件与影响因素的不同，排班模型与求解方式方法也会有所差异。

旅行商问题(TSP 问题)利用弧和节点可对乘务任务的接续进行很好的描述，在考虑避免出现乘务人员加班、保证休息时间的情况下，以乘务作业段间接续时间最小构建排班模型，借鉴TSP 问题原理与求解思路将排班过程转化为类TSP 问题，设计蚁群算法搜寻满意解，并运用案例验证模型和算法的有效性。

1 问题分析

城市轨道交通乘务排班计划是在列车开行计划、运行图以及车底周转计划已经确定的前提下进行编制。计划编制过程一般包括确定乘务基地及值乘车站(即确定换乘点)、划分乘务片段、生成乘务作业段、生成乘务工作班4 个步骤。因划分乘务片段步骤的结果只作为排班计划输入的最初条件，其组合方案优劣对后续计划整体优化影响不大，在计划编制时将第2 步与第3 步合并为1 个步骤。

乘务基地一般设在车辆段，实际运营中由于线路较短，为了保障运行效率和合理的换乘间隔，值乘车站的选取一般靠近车辆段。在运行图中去掉非轮乘站仅留下换乘点与相关时刻，第3 步生成乘务作业段过程简化示意图，排班过程简化示意图如图1 所示。以车底编号“2001”的运行任务为例，该线路有车辆段与值乘车站2 个换乘点，以司机一次作业最长时间限制将运行任务分割为乘务作业段，图中黑色粗线即代表1 个乘务作业段。不同的乘务作业段再依据相应的规则约束组合成乘务工作班。

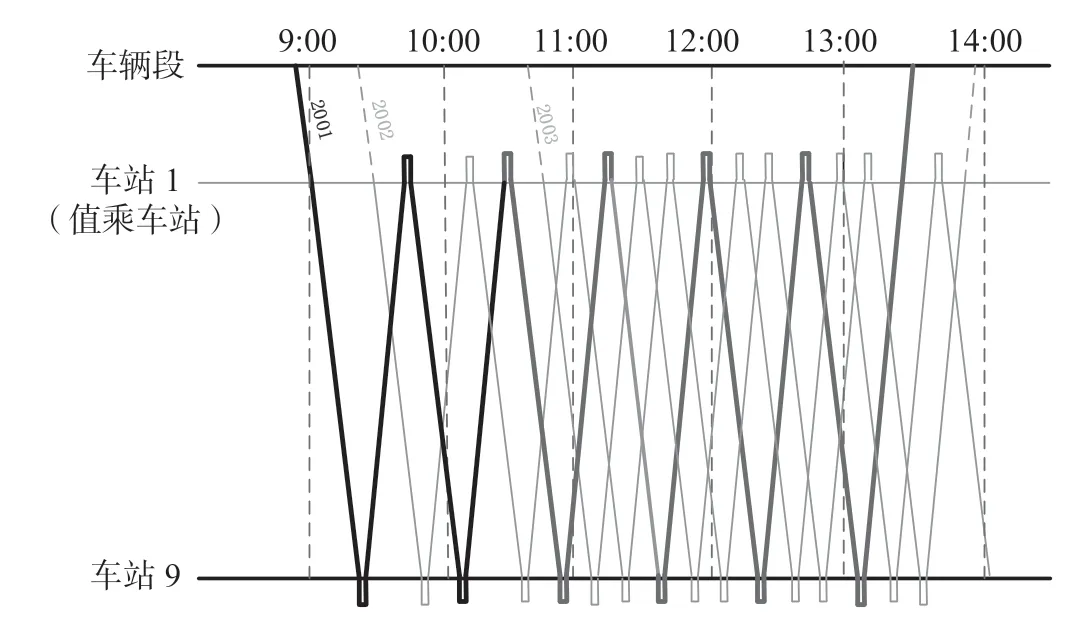
图1 排班过程简化示意图Fig.1 Simplified scheduling process

在编制乘务排班计划过程中，主要影响因素有：①乘务作业段覆盖的唯一性，即所有乘务作业段均必须被乘务任务所覆盖，有且仅有一次；②乘务作业段间接续规则，即不可连续工作，前后接续的作业段间需预留交接班、基本休息时间、整备时间等相应的时间间隔；③工作时间限制，根据《劳动法》规定的工时制度，工作班时间与司机工作时间具有相应的时长限制；④就餐约束，运营企业应在规定时段内安排司机吃饭。

2 模型构建

2.1 符号定义

2.2 乘务作业段的生成

乘务排班计划编制过程如图2 所示。城市轨道交通中，车辆启动停止频繁，驾车环境相对较差，司机容易疲劳而产生安全隐患，一般需设定司机出勤一次最大连续作业时间，即1 个乘务作业段的时间跨度。休息间隔时间过短不利于乘务人员休息，时间过长则增加了乘务人员的日工作时间。依据劳动法规定，设置乘务作业段最长时间限制Tzc与最短时间限制Tzd。

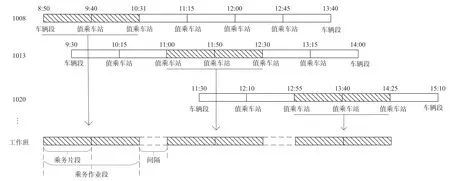
图2 乘务排班计划编制过程Fig.2 Formulation process of crew scheduling plan

设置xij为0-1 变量表示乘务片段i被乘务作业段j选中时为1，否则为0，切割乘务作业段时，需满足以下约束。

公式 ⑴ 至公式 ⑶ 表示1 个乘务作业段必须由相同车底、且时间与空间上相互衔接均无间隔的乘务片段组成；公式 ⑷ 至公式 ⑸ 表示每个乘务作业段时长应满足最短时间与最长时间限制。

2.3 乘务工作班的生成

根据乘务工作班生成步骤，考虑避免出现加班情况，安排司机正点就餐，构建作业段接续关系模型；根据乘务工作班的约束规则，1 个工作班可以由不同的车底、不相关联的乘务作业段组成，通常1个司机当天的乘务任务只需值乘1个工作班。定义yqj为0-1 变量表示作业段j被工作班q选中时为1，否则为0。乘务工作班生成模型以乘务作业段间接续时间最小为目标，可表示为

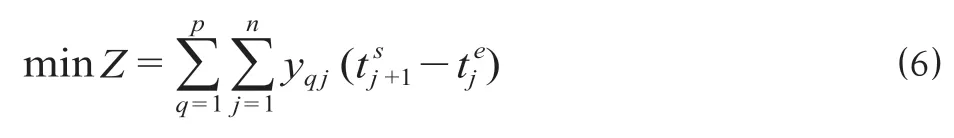
需考虑乘务作业段间接续关系、休息时间限制、乘务作业段完全覆盖等约束条件，具体如下。

（1）所有乘务作业段必须全部被乘务工作班所覆盖，有且仅有一次，可表示为

（2）司机在不同换乘点间交接班需要预留必要时间取值为Tab。定义β为0-1 变量表示接续前后乘务作业段的终止、起始车站一致即，取值为1，否则为0；司机值乘从车辆段出发的乘务作业段前需要一定的整备时间，取值为T1。定义α为0-1 变量表示当接续的下一乘务作业段起始地点为车辆段时取1，否则取0；定义γ为0-1 辅助变量，1 个乘务工作班内前后均被接续的乘务作业段时间跨度较短，其前后均在同一就餐时间段内时仅安排在前一间隔就餐。就餐时间取值为T2，就餐时间安排如图3 所示。设置司机最短的间休时间为T。

图3 就餐时间安排Fig.3 Dining time arrangement

故2 个连续的乘务作业段接续时，应满足间隔约束可表示为

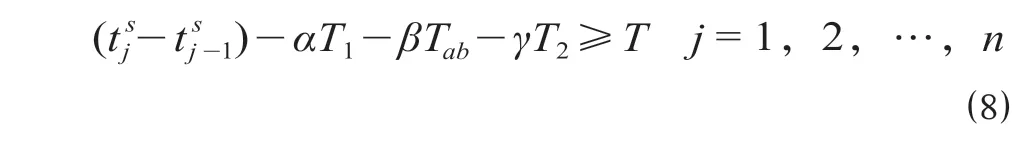
（3）根据劳动法规定，设置1 个乘务工作班的工作时间、时间跨度分别为T3，T4，乘务工作班的工作时间约束与时间跨度约束表示为

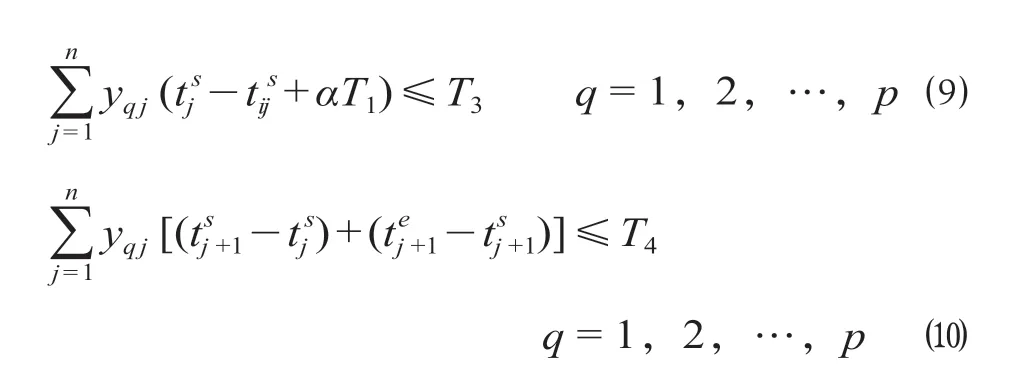
3 求解算法

3.1 类TSP 问题转化思路

1 个商人要拜访n个城市，每个城市只能拜访1 次，且最后要回到原来出发的城市，如何规划路线使得总行程最短，即为TSP 问题。在乘务工作班生成过程中，将乘务作业段抽象为带有时空属性的节点，将乘务作业段间的接续抽象为弧，每个节点有且只有1 次被选择并按照接续时间及规则依次选择节点，通过首尾虚拟点相连将此过程转化为类TSP 问题，将乘务排班计划问题转化为类TSP问题时需考虑以下2 个方面。

（1）节点具有时空属性。TSP 问题中城市节点仅具有空间位置属性，乘务排班计划中节点代表着一段时间的运行任务，选择城市时除距离限制外无其他约束，而乘务作业段间接续时前后段的终止、起始车站不一定相同，互相接续的乘务作业段需满足后者起始时刻在前者终止时刻之后，故节点间距离矩阵也并非TSP 问题中的对称矩阵，将不可接续的矩阵位置设置为极大值。

（2）乘务工作班具有时间限制。生成乘务工作班时，对驾驶时间、工作时间、每个乘务工作班时长均有限制，故需设置虚拟点。转化为类TSP 问题，乘务作业段组合过程示意图如图4 所示，虚拟点无具体含义仅用于按照约束条件隔开工作班，所有节点都被选择、覆盖后再返回虚拟点1 形成完整的回路。

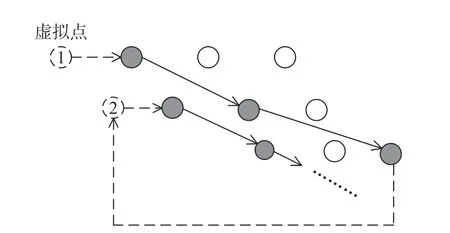
图4 乘务作业段组合过程示意图Fig.4 Combination process of crew sections

3.2 蚁群算法及流程

将生成乘务工作班步骤转化为类TSP 问题，采用求解TSP 问题、指派问题、着色图问题等取得较好效果的蚁群算法，以乘务作业段集合为输入条件，设计乘务工作班模型的求解算法如下。

（1）初始化参数。蚂蚁数量m，信息素重要程度因子α，启发函数重要程度因子β，信息素释放因子Q、最大迭代次数iter_max，迭代次数初值iter=1。根据导入的乘务作业段集合数据，计算两两作业段间的时间差，得到距离矩阵。但该问题与TSP问题计算的对称矩阵不同，后接续的乘务作业段起始时间在被接续的乘务作业段终止时间之前时，二者不可组合在一起，将此处与对角线上的值设置为一个极大值。启发函数为ηij(t)=1/dij，其中ηij(t)表示蚂蚁在作业段i时接续作业段j的期望程度。

（2）构建解空间。将蚂蚁随机置于不同出发点，将每个蚂蚁访问的第一个乘务作业段编号记录在路径表。设置禁忌表记录已访问过的作业段编号，集合allowk用于存放该蚂蚁待访问的乘务作业段编号，s为集合allowk中的一个编号。τij(t)为时间t时由节点i到节点j的信息素强度，对于每个蚂蚁k按照公式 ⑾ 计算选出其下一个访问的乘务作业段，将其对应的编号记为target2，对其进行相关约束条件判断，计算工作时间与驾驶时间，满足规定的间隔且一个工作班内工作时间与驾驶时间未超过相应限制时，记录在路径表内。之后继续选择下一个乘务作业段，当超过工作班相关时间限制时，当前工作班内作业段的选择结束，继续进行下一工作班的选择。

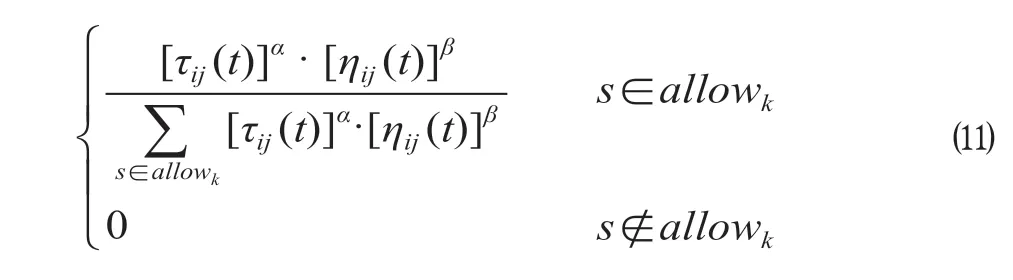
为了降低下一工作班内搜索解时的盲目性与匹配时的无效性，以及尽量减少单个乘务作业段单独成班的情况出现，增加选择节点的方式：下一乘务工作班内起点选择集合allowk中起始时刻最早的作业段，将其对应编号记为target3，target3 选择方式示意图如图5 所示。直接记录在路径表内，更新路径表、禁忌表、集合allowk。

图5 target3 选择方式示意图Fig.5 target3 selection mode

之后继续按照公式 ⑾ 概率以轮盘赌方式计算下一接续乘务作业段，判断相应约束和限制条件，如此往复直至所有乘务作业段都被选择，集合allowk为空。由于dij中设置了极大值，可能会出现集合allowk中所有乘务作业段的转移概率均为0，轮盘赌失效，表示无可接续乘务作业段，此时结束当前工作班内乘务作业段的选择。

为了区分乘务工作班，Table中依据蚂蚁行走的路径依次记录乘务作业段编号并为循环过程中禁忌表赋值；Table中赋值时增加虚拟点0，按照工作班时间与驾驶时间限制将乘务工作班间隔开。2 个路径表同一行数据对比如表1 所示，Table1 中“0—5—10—34—0”之间即为1 个乘务工作班，该乘务工作班共包含3 个乘务作业段。

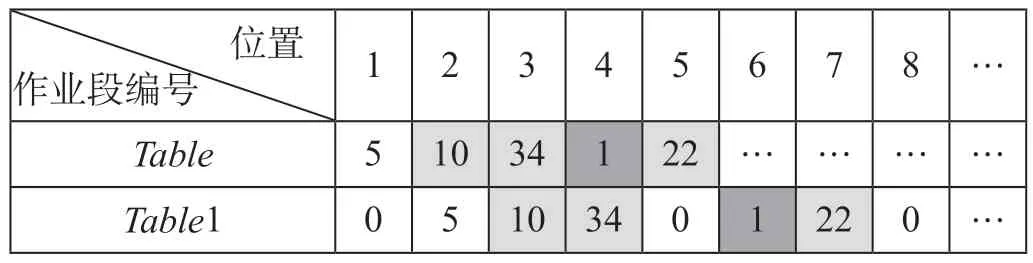
表1 2 个路径表同一行数据对比Tab.1 Comparison of the same row of data in two path tables

综上所述，在计算筛选可接续节点时共有4种情况：该节点满足全部约束可被选择；该节点满足接续顺序但不满足间隔约束；该节点满足接续顺序与间隔约束但超出工作时间或乘务工作班时间限制；上一节点无法选出可与其接续的节点，需单独成班。

（3）更新信息素、迭代寻找最佳路径。计算每个蚂蚁路径的乘务工作班内乘务作业段间时间间隔总和，以公式 ⑹ 作为蚁群算法的评价函数，所有乘务作业段间接续时间总和最小的解即为该问题最优解。每次迭代后按照公式 ⑿ 和公式 ⒀ 实时更新节点间的信息素浓度。经过循环迭代，记录最优的路径及时间长度。

式中：ρ表示信息素的挥发程度；表示第k只蚂蚁在乘务作业段i与j连接路径上释放的信息素浓度；Δτij表示所有蚂蚁在乘务作业段i与j连接路径上释放的信息素浓度之和。

（4）判断算法终止条件。若iter＜iter_max，则iter=iter+1，清空2 个路径表，并返回步骤（2）；否则，终止计算，输出最优解。

4 案例分析

以某地铁4 号线为例，该线路全长20.8 km 全部为地下线，共设18 座车站，含1 个车辆段(换乘点1)，一个值乘车站(换乘点2)，运行图中有2列车次在非值乘车站(车站3)退出服务，故司机需到换乘点1、换乘点2 交接班。排班计划时间标准参数取值如表2 所示。

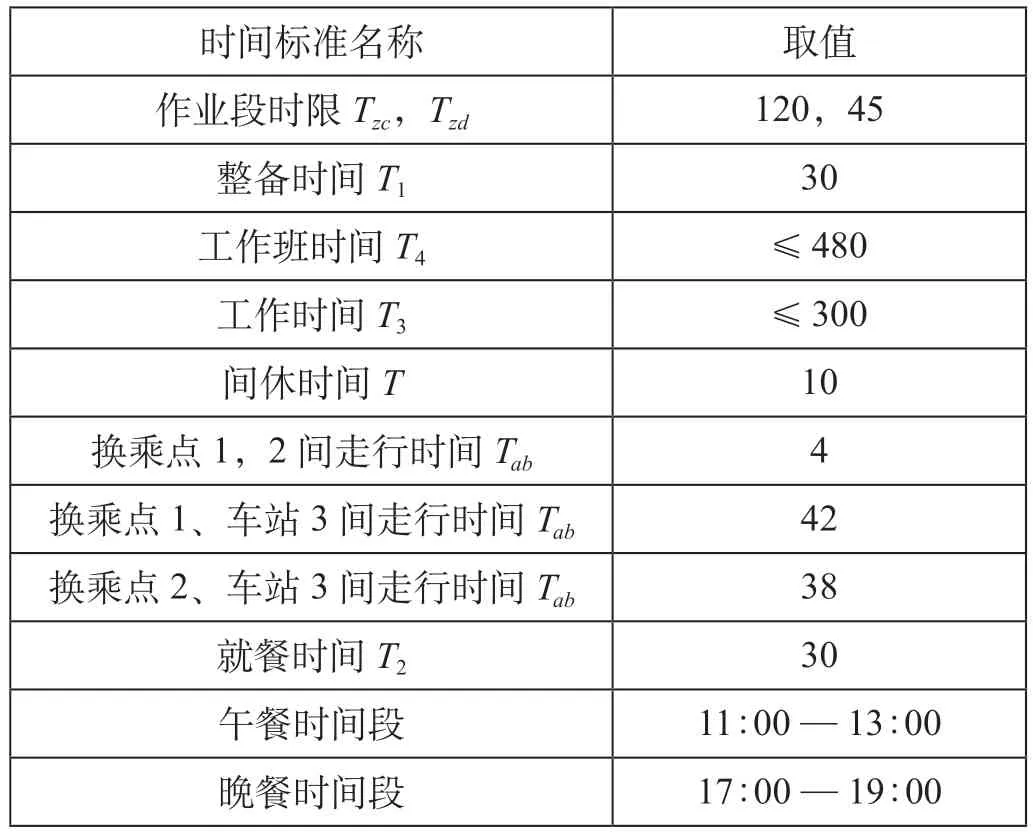
表2 排班计划时间标准参数取值Tab.2 Time standard parameter value of scheduling plan

（1）生成乘务作业段方案。根据表2 相关数据以及乘务作业段生成的思路，求得乘务作业段部分方案如表3 所示，求得乘务作业段时长分布如图6所示。切割运行图后共得到248 个乘务作业段，平均作业段时长为85.7 min，最长时长为119.77 min，最短时长为46.98 min，符合最长时间与最短时间约束。

表3 乘务作业段部分方案Tab.3 Partial scheme of crew section program

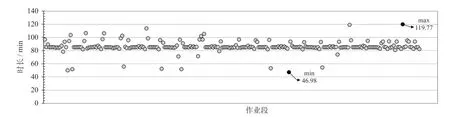
图6 乘务作业段时长分布Fig.6 Time distribution of crew sections

（2）生成乘务工作班方案。根据蚁群算法求解思路，以生成的乘务作业段集合为输入数据进行编程。蚁群算法参数取值如表4 所示。求得的乘务工作班部分方案如表5 所示，接续时间、驾驶时间、工作时间、工作班时间分布如图7 所示，迭代收敛图如图8 所示。

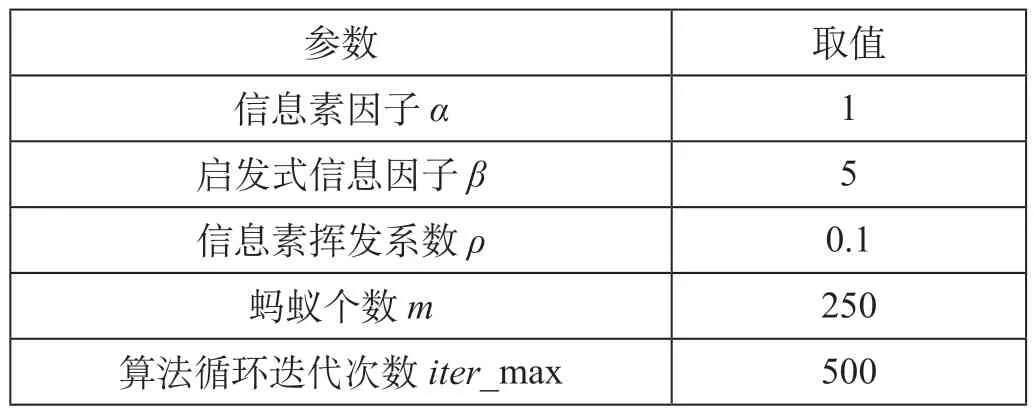
表4 蚁群算法参数取值Tab.4 Parameter value of ant colony algorithm

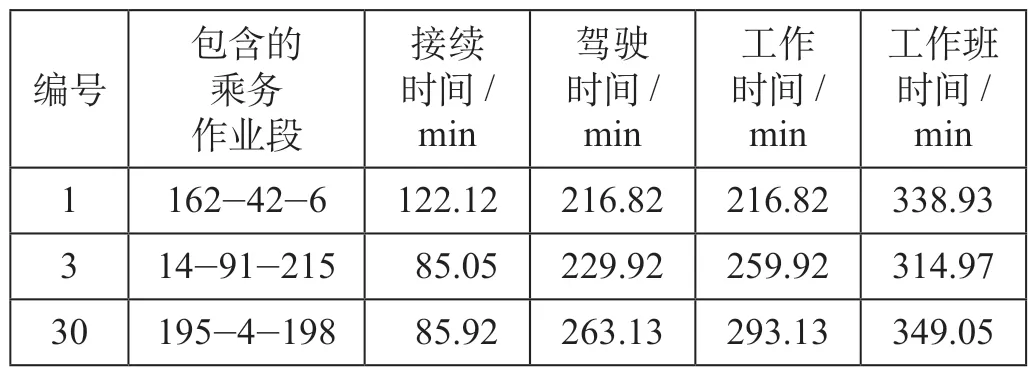
表5 乘务工作班部分方案Tab.5 Partial scheme of crew shift program

计算共得到90 个乘务工作班，从图7 中可以看出最后存在乘务作业段单独成班的情况，并且接续时间存在长短差距较大部分，说明由于不同地点交接班、就餐安排等约束较多而导致某些时间段编制较为困难。从图8 中可看出计算已得到稳定的最优解，工作班内平均接续时间为70.97 min，平均驾驶时间为236.14 min，平均工作时间为246.14 min，平均工作班时间为307.11 min，平均工作时间低于最高限制300 min，每个工作班中平均有3 个作业段。

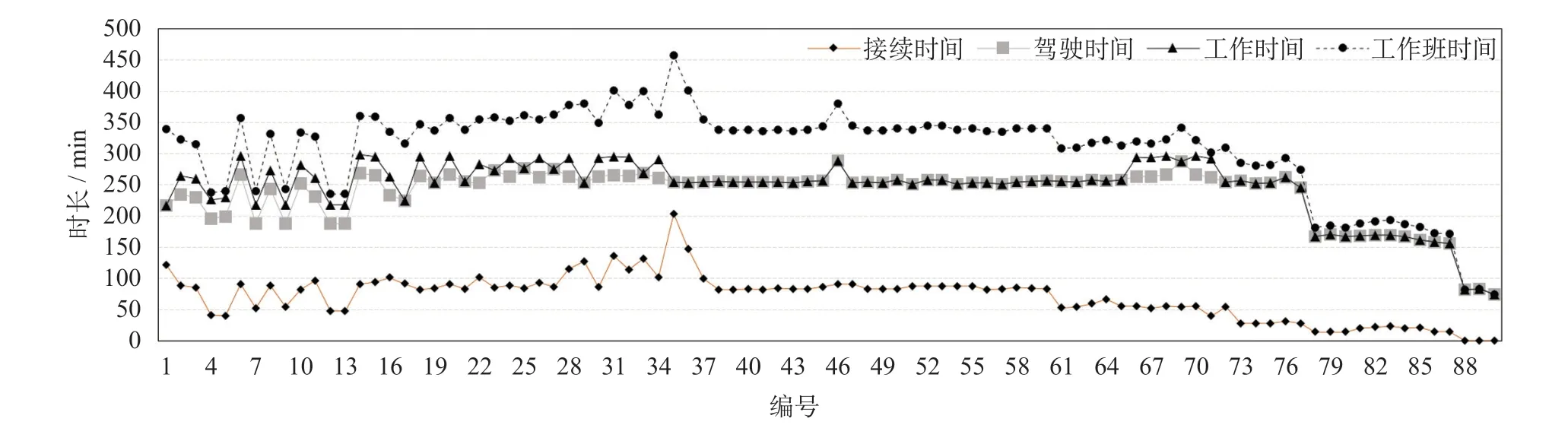
图7 接续时间、驾驶时间、工作时间、工作班时间分布Fig.7 Distribution of connection time,driving time,working time,and crew shift time

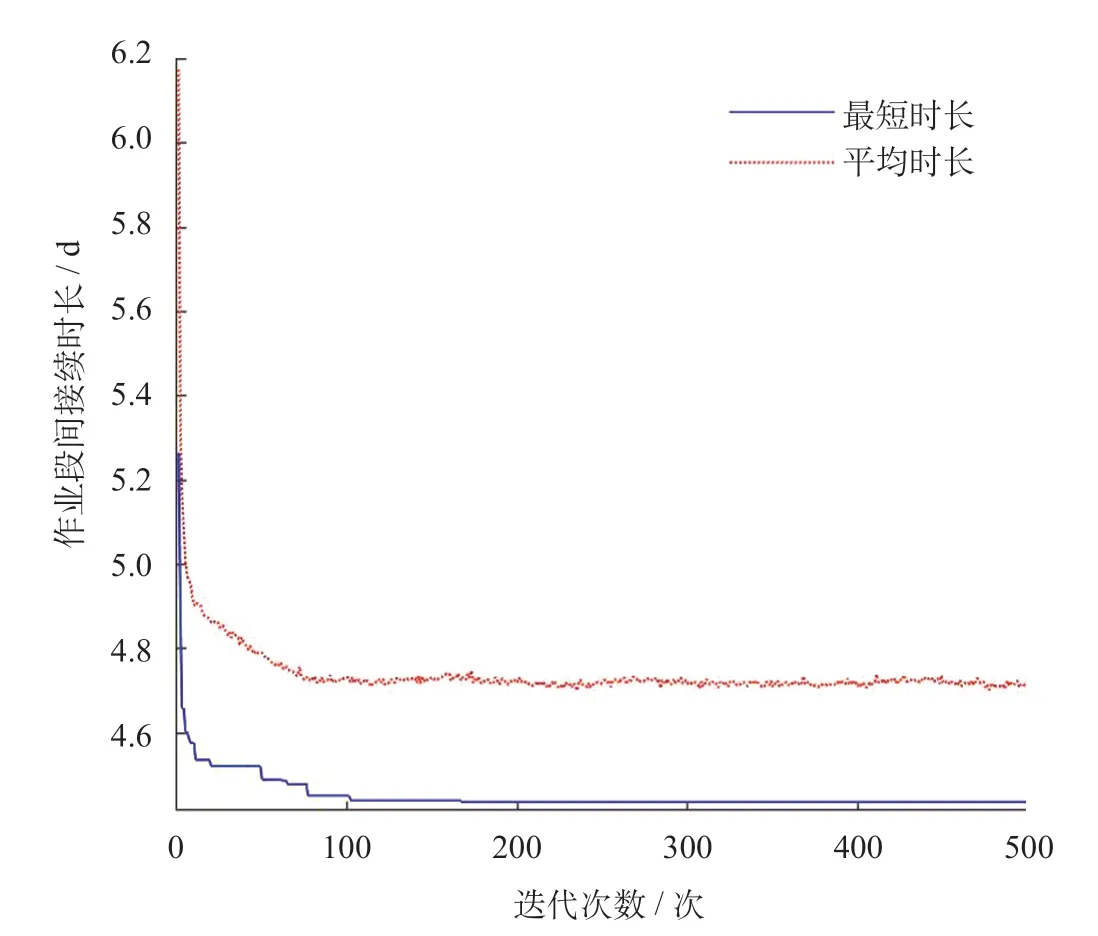
图8 迭代收敛图Fig.8 Iterative convergence diagram

5 结束语

随着城市轨道交通运营规模、建设的快速增长，乘务排班计划的质量对于提升企业运输组织效率及成本效益具有重要意义。以乘务工作班内接续时间最小为目标，将排班问题转化为类TSP 问题，设计包含虚拟点的双路径表及蚁群算法，以提高乘务人员利用率和降低运营企业人力成本。未来可在单线城市轨道乘务排班计划编制基础上，对乘务员人数最少、工作强度均衡等多目标需求，乘务规则、运营条件等不同环境下高效优质乘务排班计划的编制进行深入研究。