基于IPSO-LSTM 组合模型的城市轨道交通短时客流预测
2022-03-04赵明伟张文胜
赵明伟,张文胜
(1.济南轨道交通集团有限公司 第一运营有限公司,山东 济南 250300;2.石家庄铁道大学交通运输学院,河北 石家庄 050043)
0 引言
城市轨道交通凭借其速度快、运量大、舒适安全的特点成为城市交通的主要方式。准确、有效地对城市轨道交通短时客流进行预测,能够为城市轨道交通的运营提供可靠的技术支撑。轨道交通客流预测可分为中长期、短期和短时3 种,中长期预测主要应用在轨道线网规划与建设时期,短期预测是预测未来1 年以内的客流量,这2 种时间跨度的预测对于日常运营阶段的帮助不大,短时预测是预测15 min 之内的客流量[1],其对于城市轨道交通工作计划的安排以及列车的调度具有辅助作用。
对于客流的预测主要有3 类模型,分别是基于数理统计的模型、智能算法的模型和组合模型[2]。基于数理统计的模型有卡尔曼滤波模型[3]、自回归移动平均模型、季节性自回归移动平均模型等,这类方法较为简单,操作容易,但容易受到客流呈线性假设的限制,对于实际场景中的非线性客流无法准确地进行预测[4]。基于智能算法的模型,能够利用自身的学习能力和自适应能力对客流的非线性特征进行捕捉,智能算法包括支持向量机、贝叶斯网络和人工神经网络等,Roos 等[5]采用一种动态贝叶斯网络方法来预测短期客流;Li 等[6]用径向基函数神经网络预测单站客流。近年来,循环神经网络(RNN)、长短时记忆神经网络(LSTM)、门控循环单元神经网络和卷积神经网络等模型,在捕捉时空关系方面具有优越的性能而受到广泛重视,Duan 等[7]利用LSTM 模型预测行程时间,取得很好的预测效果,并比较不同时间长度模型对预测误差值的影响。组合模型,一般是结合2 种或3 种模型的优势,能够有效提高模型的预测精度,组合模型有季节性差分自回归滑动平均模型、神经网络和遗传算法的组合模型[8]、小波-支持向量机组合模型[9]、循环门控单元和图卷积神经网络组合模型[10]、集合经验模态分解和神经网络组合模型[11]等,组合模型已成为客流预测的趋势。
LSTM 模型是一种改进的时间递归神经网络,适合于处理长时间序列的数据,但是LSTM 模型的参数较难确定,不同参数的选取对预测结果具有较大的影响,一般采用试错法或经验法确定参数,效率较低,针对此问题,利用粒子群(PSO)算法来确定LSTM 的参数,但PSO 算法存在容易陷入局部极值的问题,需对其算法位置更新公式和速度更新公式进行改进,并利用遗传算法中的变异机制,引入自适应变异函数,提高粒子的寻优能力,故通过利用一种改进的粒子群(IPSO)算法对LSTM 模型的迭代次数、学习率和隐含层的神经元个数进行寻优,构建IPSO-LSTM 城市轨道交通短时客流预测组合模型,对客流进行预测。
1 IPSO-LSTM 短时客流预测组合模型的建立
1.1 IPSO 算法
PSO 算法最早是由Eberhart 和Kennedy 于1995 年提出的,是一种全局搜索最优值的算法[12]。假设在d维搜索空间中,粒子群中有N个粒子,其中第i个(i=1,2,…,N)粒子在d维空间中的位置为Xi=(Xi1,Xi2,…,Xid),第i个粒子的速度为vi=(vi1,vi2,…,vid),第i个粒子的最优位置为Xpbest=(Xp1,Xp2,…,Xpd) (p=1,2,…,N),即个体最优值,全局最优值为Xgbest=(Xg1,Xg2,…,Xgd) (g=1,2,…,N),即所有粒子在搜索过程中的历史最优位置。PSO 算法的核心就是通过不断地调整粒子的速度和位置,使粒子逐步地靠近最优位置,粒子的速度和位置计算公式为


PSO算法的惯性权重w和时间因子t是固定的,不能满足算法的自适应搜索,导致算法的全局搜索能力减弱,容易陷入局部极值。为解决上述问题,分别将PSO 算法的w和t进行改进,增强PSO 算法的全局搜索能力,并引入遗传算法的变异机制,赋予PSO 算法跳出局部范围的能力,使PSO 算法按照先全局搜索后局部搜索的搜索方式,逐步逼近最优值,计算过程如下。
(1)计算自适应惯性权重。固定的w会减弱算法的全局寻优能力并减慢算法的收敛速度。为此提出了一种基于全局最优位置和局部最优位置的变化来确定w的计算方法。通过监视粒子的全局最优位置和个体最优位置,根据二者之间的数值变化不断地调整w的大小,使其自适应变化。自适应惯性权重w的计算公式为
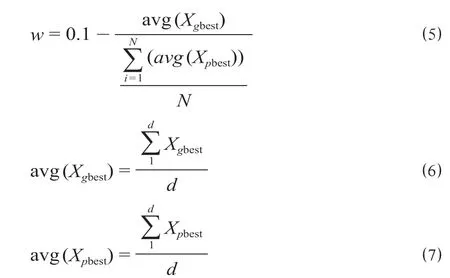
式中:avg (Xgbest)表示d维搜索维度下Xgbest的均值;avg (Xpbest)表示d维搜索维度下Xpbest的均值;N表示种群的个数。
每一次迭代后会有一个d维的Xgbest和N个d维的Xpbest,采用全局最优值和个体最优值比值的变化,不断地动态调整w的大小,打破固定w对算法搜索性能的影响。
(2)计算自适应时间因子。针对物理学中位移和速度量纲不同的问题,引入时间因子t。传统粒子群算法中的时间因子默认为1,导致粒子易在最佳位置附近振荡,无法及时找到最优解,故引入与迭代次数m相关的自适应时间因子t,其计算公式为

式中:mmax表示最大迭代次数。
随着迭代次数的增加,时间因子t逐渐减小,根据公式 ⑵,粒子移动的步长逐渐减小,粒子的位置变化逐渐变小,粒子先以大步长做全局搜索后再以小步长做局部搜索,提高搜索的精度。
(3)构建自适应变异函数。受到遗传算法的变异机制的启发,提出了一种自适应的变异函数,赋予粒子跳出局部范围的能力:当rand ≥ Prob 时,粒子发生变异,使粒子均匀地散布在整个空间,自适应变异函数计算公式为
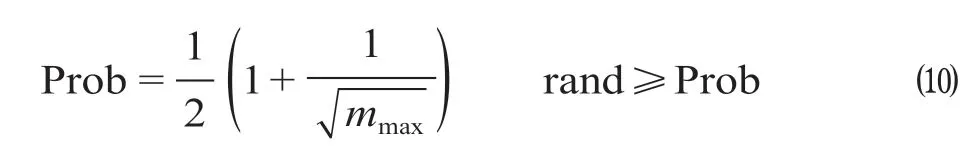
式中:Prob 表示自适应变异函数;rand 表示[0,1)之间的随机数。
当迭代次数较少时,Prob 较小,rand ≥ Prob的机率较大,粒子容易发生变异,较容易跳出局部范围,从而进行全局搜索;随着迭代次数的增多,Prob不断增大,而rand ≥ Prob的机率就会变小,粒子发生变异的机率就会变小,从而在小范围内进行局部搜索,粒子以一种先全局搜索后局部搜索的搜索方式,先粗略寻找,后精确寻找,最终完成收敛。
1.2 LSTM 模型
LSTM 模型是Hochreiter 和Schmidhuber 在1997 年提出的,该模型可以进行自我衡量,特别适合于处理具有一定的时间间隔的数据序列。LSTM 记忆单元结构图如图1 所示。
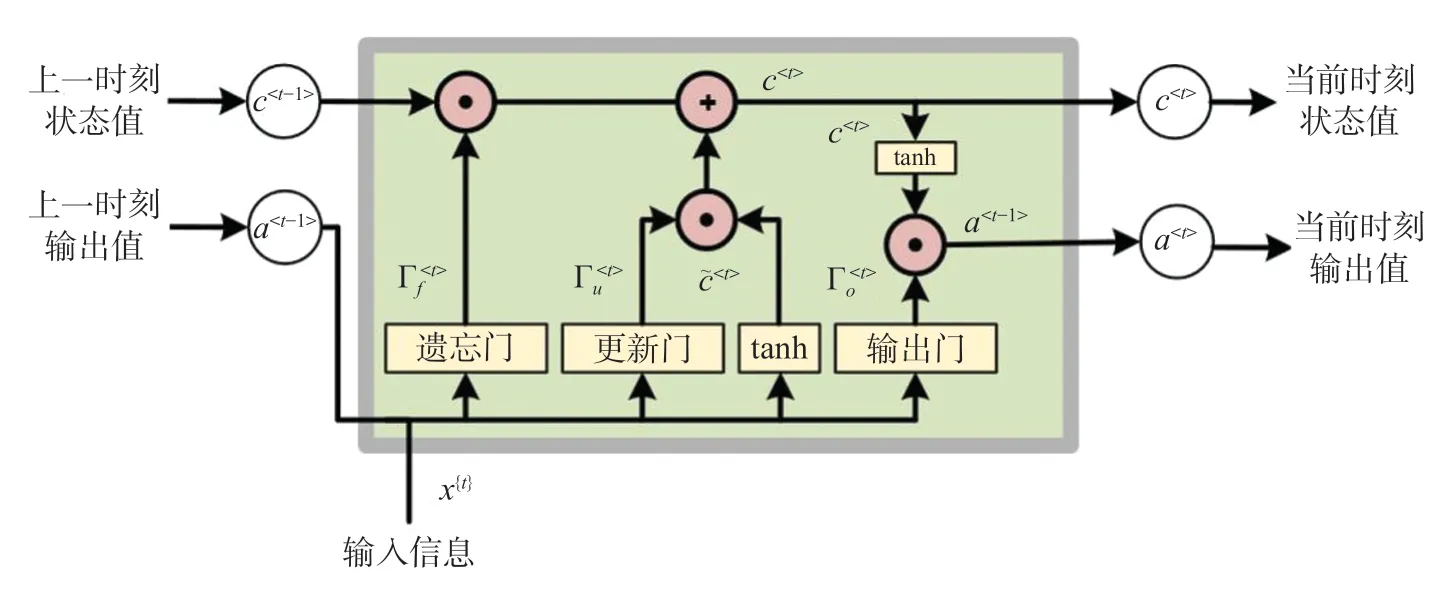
图1 LSTM 记忆单元结构图Fig.1 Structure of LSTM neural network unit
LSTM 模型每一层的神经元都具有多个“门”的结构,这使得误差在传递过程中,部分误差可以直接通过“门”,这样就不用再归因于所通过的神经元,误差可以原封不动的传到下一层,无论数据有多长,梯度都不会完全消失或爆炸,LSTM模型预测过程具体如下。
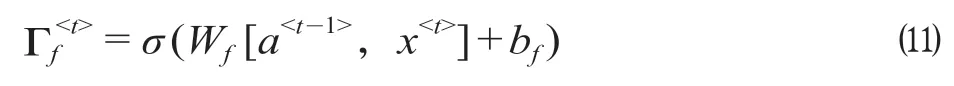
式中:σ表示Sigmoid 函数;Wf表示遗忘门的权重矩阵;bf代表遗忘门的偏置项;[a
(2)计算更新门Γu
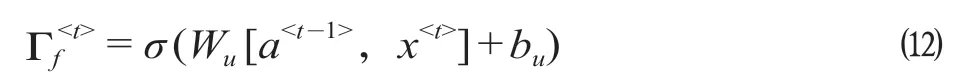
式中:σ表示Sigmoid 函数;Wu表示更新门的权重矩阵;bu表示更新门的偏置项。
输入的单元状态为c~
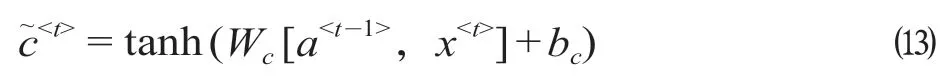
更新门的2 个部分会将c
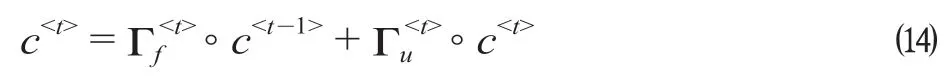
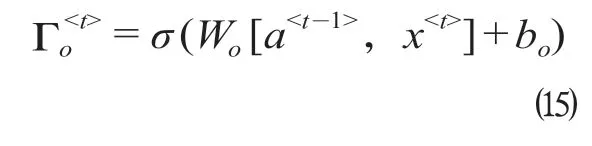
式中:Wo表示计算单元状态的权重矩阵;bo表示计算单元状态的偏置项。
LSTM 模型最终的输出是由输出门和单元状态共同确定的,其计算公式为

虽然LSTM 模型具有明显的优点,但是其参数较难确定,不同参数的选取对预测结果有很大的影响,可借助IPSO 算法来弥补LSTM 的不足。
1.3 IPSO-LSTM 模型的建立
通过构建IPSO-LSTM 城市轨道交通短时客流预测组合模型,利用IPSO 对LSTM 的迭代次数、学习率以及隐含层的神经元个数进行寻优,隐含层层数为2 层,并利用IPSO-LSTM 城市轨道交通短时客流预测组合模型对客流进行预测,提高LSTM模型的预测精度。IPSO-LSTM 城市轨道交通短时客流预测组合模型的构建过程具体如下。
(1)初始化粒子群参数。确定种群的规模、迭代次数、学习因子、搜索维度以及位置和速度的取值范围。城市轨道交通短时客流预测中待寻优的参数有4 个,故搜索维度为4 维。
(2)初始化粒子的位置和速度。随机生成1 个粒子,Xi=(θ,β,α1,α2),θ表示LSTM 的迭代次数,β表示学习率,α1表示第一层隐含层的神经元个数,α2表示第二层隐含层的神经元个数,粒子的速度vi=(vi1,vi2,vi3,vi4),产生一组0~ 1 均匀分布的随机样本值,随机样本取值范围是[0,1)。确定LSTM 的其他参数,预测方案为单步预测。
(3)确定粒子群算法的适应度函数。用初始化后的粒子群参数构建LSTM,将训练集的实测值与预测值的均方误差作为粒子群的适应度函数。
(4)计算粒子在每一次迭代中的位置并计算适应度值。通过与初始位置的适应度值作比较,确定个体最优位置Xpbest,进而确定群体最优位置Xgbest。
(5)进行预测。利用IPSO 算法寻找最优参数,确定迭代次数、学习率以及隐含层的神经元个数。对LSTM 模型进行训练,达到最大迭代次数后,将数据输入训练好的模型进行预测,输出最终预测结果,并对误差进行分析。
2 客流预测实例分析
数据来源于上海市2015 年4 月1 日至4 月30日期间的一卡通刷卡数据,利用计算机软件对所构建的模型进行验证。分别构建神经网络(BP)模型、LSTM 模型、PSO 算法和LSTM 模型组合(以下简称“PSO-LSTM 模型”)、IPSO-LSTM 模型对陆家嘴站的客流进行预测。
首先对数据进行处理,获得可用于预测的时间序列数据。利用Pearson 相关系数对工作日和非工作日客流进行相关性分析,得到工作日与非工作日数据的相关性分析如表1 所示。由表1 可知工作日数据之间相关性显著、非工作日数据之间相关性显著,属于高度相关性,故需从工作日和非工作日2个角度,分别进行客流预测。
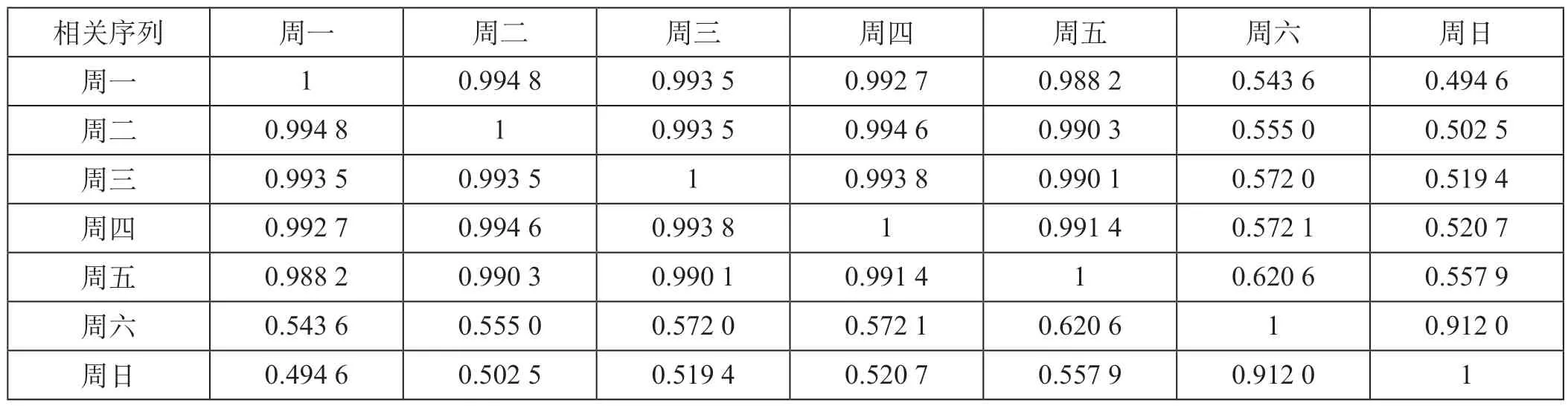
表1 工作日与非工作日数据的相关性分析Tab.1 Correlation analysis of data on working days and non-working days
短时客流具有非线性、非平稳性和强随机性的特点,相比于15 min,10 min 的客流预测间隔,5 min 的时间间隔更小,客流的变化趋势更具有波动性,随机性更强,预测难度更大,因此采用的时间间隔为5 min。为减少数据噪声对预测性能的影响,利用经验模态分解法将数据分解为多个IMF分量和1 个残差。以陆家嘴站的进站客流预测为例,预测未来一天的客流数据,预测的时间范围为5 :30 :00—23 :00 :00,以5 min 为时间间隔汇总一天当中共210 个时间段的客流数据。将4 月1 日至4 月30 日期间21 个工作日中的20 个工作日的数据作为训练集,剩下的1 个工作日的数据作为测试集;将9 个非工作日中的8 个非工作日的数据作为训练集,剩下的1 个非工作日的数据作为测试集。
其中LSTM 模型的输入层和输出层均为1 个神经元,利用Adam 优化器训练LSTM 模型。LSTM和BP 模型最大迭代次数为20 次;PSO 算法中w=0.8,c1=1.5,c2=1.5,r1=0.8,r2=0.3,粒子数量为2,维度为4,进化次数为20 次,Xi=(θ,β,α1,α2)中θ的取值范围为[100,500],β的取值范围为[0.001,0.01],α1和α2的取值范围为[1,200]。得到工作日与非工作日的BP 模型预测结果如图2 所示,LSTM 模型预测结果如图3 所示,PSO-LSTM 模型预测结果如图4 所示,IPSOLSTM 模型预测结果如图5 所示。
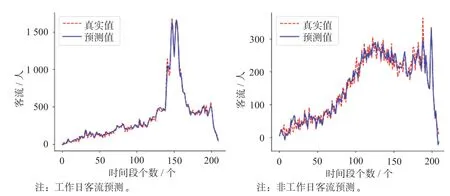
图2 BP 模型预测结果Fig.2 Prediction results of BP model
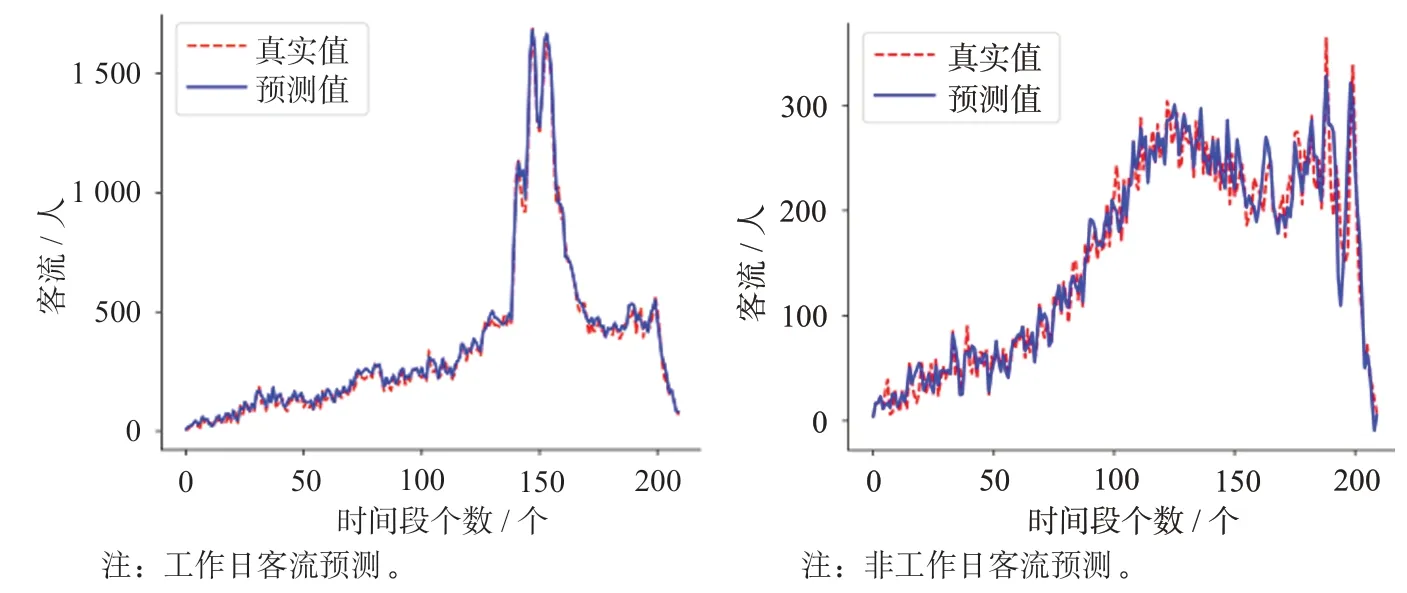
图3 LSTM 模型预测结果Fig.3 Prediction results of LSTM model
图4 PSO-LSTM 模型预测结果Fig.4 Prediction results of PSO-LSTM model
对城市轨道交通短时客流预测模型的精度进行判定,采用平均绝对百分比误差(MAPE)、均方根误差(RMSE)、平均绝对误差(MAE)和决定系数(R2) 4 种评价指标进行误差分析。MAPE,RMSE,MAE,R2的取值为短时客流预测模型独立运行10 次之后的平均值,得到4 种预测模型的误差值如表2所示。由表2 可知,综合工作日和非工作日的预测结果,IPSO-LSTM模型的预测误差均小于其他3 种预测模型。对于工作日的客流预测,IPSO-LSTM 模型相比于LSTM 模型的MAPE,RMSE,MAE 分别减小30.60%,26.03%,23.45%;IPSOLSTM 模型的决定系数达到了0.994 7。对于非工作日的客流预测,IPSO-LSTM 模型相比于LSTM 模型MAPE,RMSE,MAE 分别减小 12.87%,28.45%,26.26% ;IPSO-LSTM 模型的决定系数达到了0.973 9。由上述计算可见,IPSO 算法明显提高了LSTM 模型的预测精度,且优于BP 和PSO-LSTM,预测结果的决定系数在0.97 以上,可知IPSO-LSTM 模型在城市轨道交通短时客流预测上具有更高的精度。

表2 4 种预测模型的误差值Tab.2 Error values of four prediction models
根据进站客流晚高峰和平峰的客流预测结果进行对比分析,4 种模型晚高峰时段客流预测误差绝对值对比如表3 所示,4 种模型平峰时段客流预测误差绝对值对比如表4 所示。由表3 和表4 可知,IPSO-LSTM 模型对于晚高峰和平峰的客流预测都达到了较好的预测效果,并且相比于LSTM,PSOLSTM,BP 模型,IPSO-LSTM 模型的误差更小。
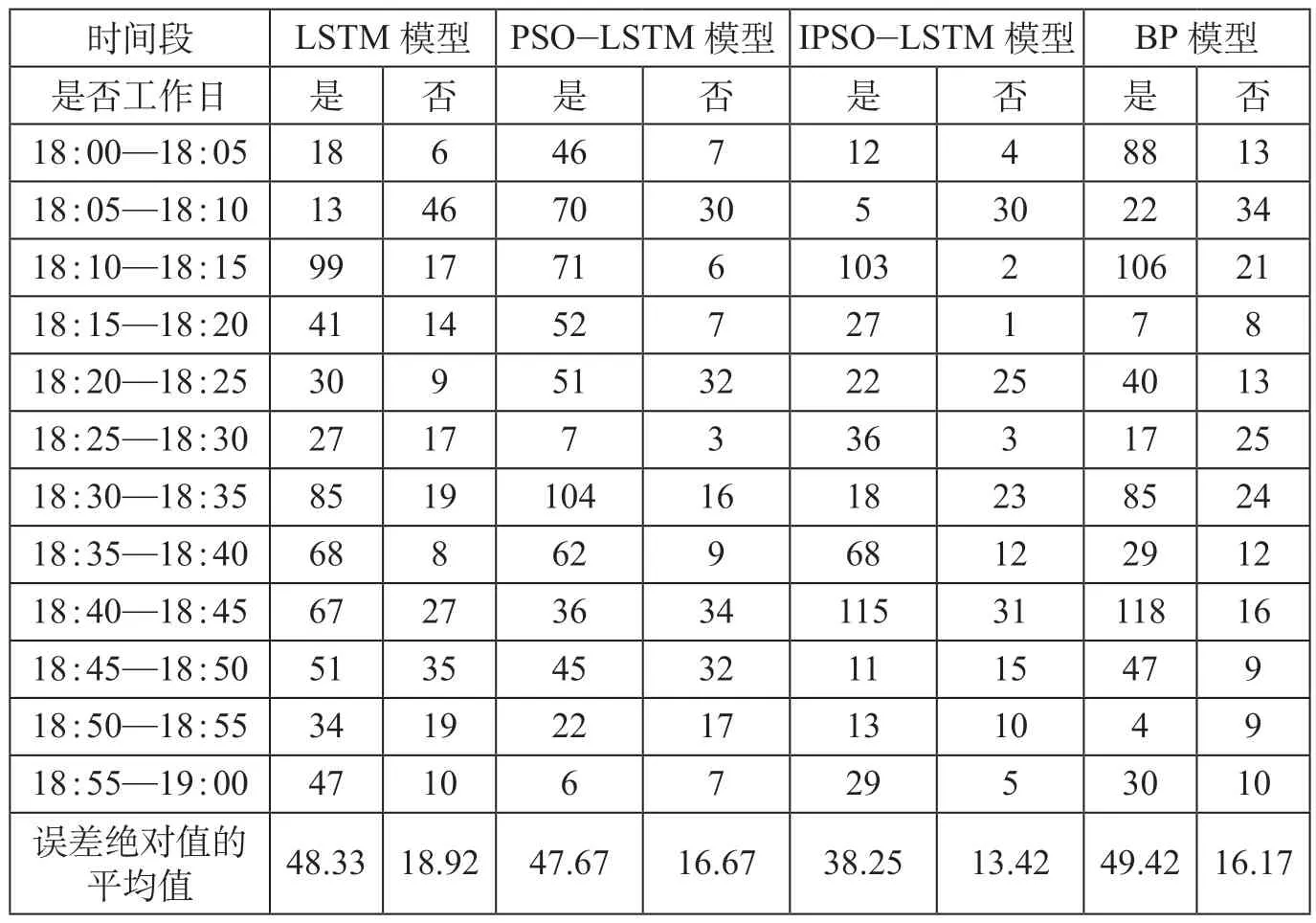
表3 4 种模型晚高峰时段客流预测误差绝对值对比Tab.3 Absolute value comparison of passenger flow prediction errors of four models during evening peak hours

表4 4 种模型平峰时段客流预测误差绝对值对比Tab.4 Absolute value comparisonof passenger flow prediction errors of four models during the peak period
3 结论
通过改进的粒子群算法优化LSTM 模型的学习率、迭代次数和隐含层的神经元个数,利用优化后的参数构建IPSO-LSTM 模型,对城市轨道交通短时客流进行预测,得到具体结论如下。
(1)通过对粒子群算法的改进,克服粒子群算法存在的问题,提高算法的搜索性能,预测结果表明改进的粒子群算法具有更好的寻优效果。
(2)将模型进行组合可以充分地利用2 种模型的优势:IPSO 算法可以更好地确定LSTM 模型的迭代次数、学习率和隐含层神经元的个数,以此来提高预测模型的精度,IPSO-LSTM 模型对工作日和非工作日客流预测均达到较好的预测精度。
(3)仅对工作日和非工作日(周六日)的客流进行预测,由于数据有限,未能涉及节假日的客流预测,下一步的研究重点是利用节假日客流数据完善客流的预测。
