基于现场实测数据的半潜式平台运动响应分析和极值预测研究

孙刘璐，于思源，武文华, 2，谢 彬，王世圣

(1. 大连理工大学 运载工程与力学学部工程力学系 工业装备结构分析国家重点实验室，辽宁 大连 116024; 2. 大连理工大学 宁波研究院，浙江 宁波 315000; 3. 中海石油(中国)有限公司研究总院，北京 100027)

近年来，国际上对海洋油气资源开发日益关注，海洋浮式平台成为深远海油气开采的主力装备。半潜式平台(semisubmersible platform)具有良好的运动性能，广泛应用于世界各个海域的海洋石油开采。半潜式平台在深海中承受海洋环境荷载作用，尤其在台风等极端天气下，半潜式平台将可能发生稳性失效或结构的屈服、屈曲和疲劳等强度失效行为，如发生管线或杆件等结构断裂或浮筒结构的破损等事故，可能导致人员伤亡以及巨额的财产损失。

目前对海洋平台多年一遇响应极值的研究大多基于水动力学数值模拟或缩比水池试验。Sen[1]和Qiu等[2]利用时域格林函数对水面和水下浮体在波浪作用下大幅运动进行研究；Zhang和Beck[3]对瞬时大幅运动开展研究，基于研究成果开发了程序；Ran等[4]和Lake等[5]基于水动力模型试验对半潜式平台在波浪作用下的运动特性开展了研究。由于模型边界条件的简化、比尺效应以及现场条件和模拟条件的不一致性等，数值模拟与模型试验结果难以直接应用于工程设计与校核。

现场原型监测方法作为一种直接、有效的研究手段，通过从现场获得的常年载荷和响应监测数据，与概率统计等方法紧密结合，可以为水动力学仿真分析提供参考，为平台的安全作业提供支持。BMT公司在1987年对一座服役的TLP平台——Joliet TLWP平台进行了最早的浮式平台在位测量工作，对环境荷载参数(风、波浪和海流)和浮体六自由度运动情况进行测量[6]；挪威建立了第一座混凝土船体的TLP平台(Heidrun TLP)，构建了一套与平台使用寿命相当的原型测量系统，用于收集平台的环境信息、张力腿张力和运动响应信息，获得的实测数据用于对浮体在恶劣海洋环境中运动行为开展研究[7]；魏跃峰等[8]对“南海奋进号”FPSO开展了连续2年的现场测量，对南海FPSO运动行为进行了研究。

基于“南海挑战号”半潜式平台六自由度监测数据开展统计分析，利用广义极值分布拟合每日浮体六自由度响应极值的分布规律，进而开展了不同重现期下的响应极值预测研究，并基于多年一遇的极值预测结果与平台设计指标对比，分析结果对平台的作业具有指导意义。

1 半潜式平台现场监测和运动响应分析

1.1 半潜式平台现场监测介绍

“南海挑战号”FPS是我国生产型半潜式生产平台，位于南海流花海域，流花油田的开发模式由水下生产系统、半潜式浮体、海底管线和浮式储/输油轮(FPSO)等组成，平台工作水深为260～305 m。自2011年以来，在“南海挑战号”FPS建立了原型监测系统，开展了原型监测工作，为我国300 m水深油气资源开发积累了原始现场数据[9]。“南海挑战号”FPS监测系统布局如图1所示。

图1 “海挑战号”FPS监测系统布局Fig. 1 Global layout of prototype monitoring system built in “Nanhai Tiaozhan” FPS

对于平台六自由度响应信息的现场监测，采用惯性导航系统(inertial navigation system，简称INS)测量浮体的横摇、纵摇和艏摇信息，同时，利用双GPS(global positioning system)天线对INS系统的长期累积误差进行修订，精度为0.1°；采用星际差分GPS测量平台浮体的相对地理坐标系的定位和高程，并转化成平台浮体的横荡、纵荡和垂荡，其中横荡、纵荡测量精度为厘米级，垂荡测量精度为40 cm。惯导与GPS系统安装于船艏监测站内，其外接两个天线安装于监测站顶部，间距约为3 m。图2给出了某日平台的六自由度原始监测数据。

图2 半潜式平台六自由度响应典型样本数据Fig. 2 Typical 6-DOFs sampling monitoring data of semisubmersible platform

1.2 平台六自由度响应监测数据分析

1.2.1 平台六自由度响应数据

数据采集自“南海挑战号”半潜式平台2013至2014一年的六自由度响应数据，提取每日的横摇、纵摇、艏摇、横荡、纵荡和垂荡的极值。

1.2.2 数据处理过程

1) 选取平台一年实测六自由度响应数据，对监测数据中的异常值进行数据清洗和更正处理；

2) 对实测的平台经度、纬度、高度数据进行坐标转换，得到平台的横荡、纵荡、垂荡三个自由度数据；

3) 选取六自由度响应的每日极值整理成数据集。

在海洋工程的极值预测中，常采用Weibull、Gumbel等极值分布模型。但海洋环境荷载多变以及平台结构响应复杂，每个自由度适用的模型可能不同。广义极值分布模型具有三个待定参数，相比于Gumbel等模型具有更高的适应性，因此得到了广泛的应用。金光炎[10]详细地探讨了广义极值分布的统计特性，首次研制了该分布的离均系数表，并给出了水文频率计算中的示例；刘聪等[11]引入广义极值分布模型，给出该模型参数的极大似然估计的计算公式，由此导出设计基本风速及其置信上限的计算方法，并采用南通气象观测站的年最大风速资料进行实证研究；谢波涛[12]采用了多维复合极值分布理论，根据显著波高推算波峰高度并与天文潮、风暴潮等叠加，计算不同联合重现期的平台高度。

标准的广义极值分布分为3种：Ⅰ型Gumbel分布、Ⅱ型Frechet分布、Ⅲ型Weibull分布。函数定义为：

(1)

式中：x为每日响应极值；μ，ξ∈R，μ为位置参数；σ为尺度参数，σ>0；ξ为形状参数。ξ=0时，为Ⅰ型Gumbel分布；ξ>0时，为Ⅱ型Frechet分布；ξ<0时，为Ⅲ型Weibull分布。三种极值分布各有特点：Weibull分布值存在上限，意味着其最大值不能超过一个固定值，Frechet分布概率密度分布函数比Gumbel概率密度分布尾部更长，从而大极值出现的可能性更大。通过对三种类型极值分布函数的统一，解决了只能用一种分布模型的局限性[13]。

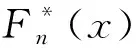
假设连续分布函数为F(x)，K-S检验的步骤如下：

① 从一年内的六自由度响应数据总体抽取容量为n=365的每日极值样本，并把样本观测值按由小到大的次序排列；

② 求出经验分布函数

(2)

③ 假定每日六自由度响应极值服从某一分布规律，计算观测值处的每日响应极值理论分布函数F(x)的值；

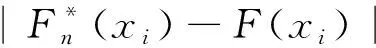
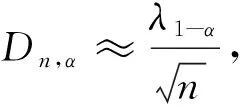
⑦ 若由⑤算出的Dn>Dn,α，则拒绝原假设，若Dn≤Dn,α，则接受原假设，并认为原假设的理论分布函数可以用于拟合样本数据的分布，六自由度响应极值符合假定的分布。

1.2.3 响应的分析结果和结论

基于上述的极值分布理论，对一年的六自由度响应进行分析。以横荡为例，取每日横荡极值作为研究目标，统计一年内的基本统计信息(均值、极值、极差、方差、偏度、峰度)，如表1所示，可以发现横荡在一年中的平均值为2.442 m，极值达到4.860 m，极差与方差的值较大，说明在一年内海洋环境复杂多变；偏度为正值，因此分布的形态为正偏；峰度小于3，因此分布相较于高斯分布平缓。综合以上的特征，也说明选取广义极值分布的合理性。

表1 横荡统计值

选择置信度为0.95，假设横荡符合广义极值分布的情况下，样本经K-S检验通过，可以认为，平台的横荡服从广义极值分布。其中，三个参数分别为ξ=-0.172，σ=0.894，μ=2.054，属于Weibull分布。概率密度以及概率分布如图3所示，从图3中可以看出，横荡的极值在一年中的分布可以认为服从广义极值分布，拟合效果较好。

图3 横荡概率密度及分布Fig. 3 The probability density and distribution of sway

用上述的方法处理纵荡、垂荡、横摇、纵摇、艏摇，均通过置信度为0.95的K-S检验，得到的概率密度与概率分布如图4所示。

表2给出了平台六个自由度监测响应的每日极值分布所拟合出的参数以及分布类型。

从表2中偏态参数可以看出，横荡、纵荡、艏摇属于右偏分布，其右端的尾部较长，均值集中在左侧值较小的部分；而垂荡、横摇、纵摇为左偏分布，均值集中在右侧值较大的部分。通过ξ可知，除艏摇服从Gumbel分布外，其余响应均服从Weibull分布。

2 平台六自由度响应的极值预测

2.1 六自由度响应多年一遇极值预测

海洋环境和结构响应的复杂性导致海洋平台在作业中常常面临失效风险。海洋平台除了面临结构疲劳损伤问题外，还因本身浮式结构运动响应而面临着更为复杂的结构失效问题。据统计，其中我国海洋平台由于响应过大而引起的失效就有数例。1979年11月，中国渤海2号平台在拖航作业中失稳、倾覆，造成72人死亡；2010年9月，中国胜利油田3号平台倾斜45°，造成1人失踪。

基于上述响应过大导致的平台失效，对平台六自由度响应进行极值预测，计算在不同重现期下，平台对应的六自由度响应极值。

重现期是指在一定数据记录统计时段内，大于或等于某水文变量在较长时期内重复出现的平均时间间隔，常以多少年一遇表达。把重现期的概念引入到本例中响应分析上来，计算多年一遇所对应的响应极值。

设每日响应极大值x的概率密度函数为f(x)，其分布函数F(x)为：

N年一遇的响应极大值xp出现的概率为P(x)，其计算公式：

利用广义极值分布模型，对六自由度响应进行1年一遇、10年一遇、25年一遇，50年一遇，100年一遇的重现期极值预测，具体数值如表3所示。

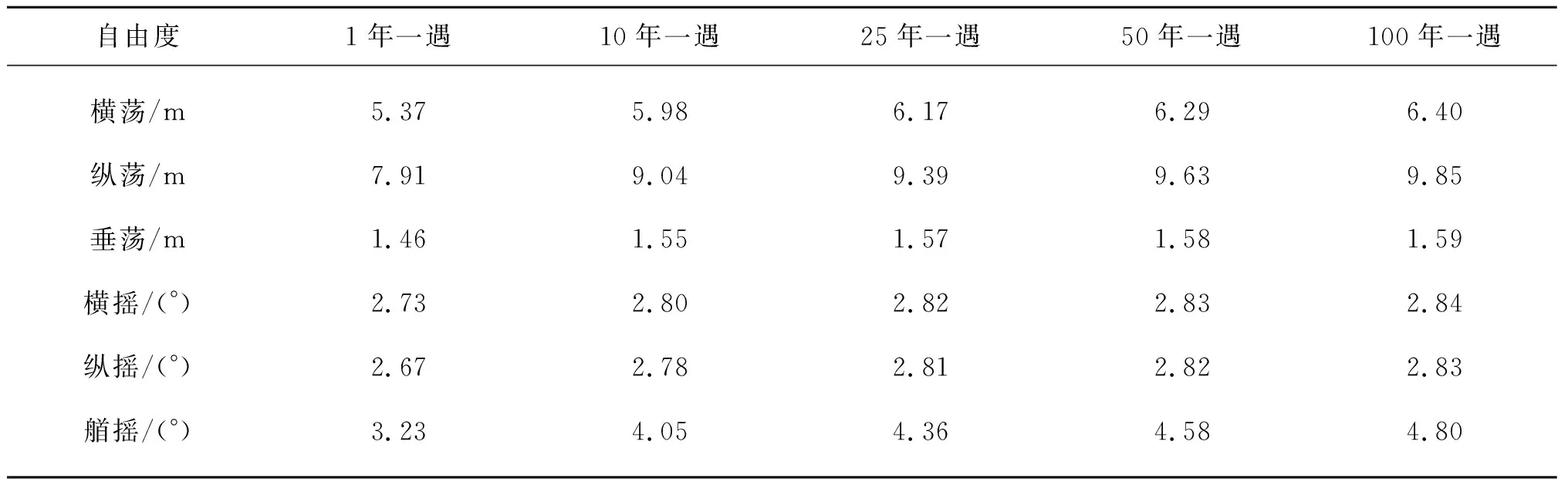
表3 平台六自由度响应在不同重现期下的极值

2.2 六自由度响应极值预测和设计指标的对比分析

半潜式平台具有良好的运动性能，在正常作业情况下，半潜式平台垂荡量不大于1.5 m，横、纵荡响应不大于水深的7%，横、纵摇不大于3°。按照南海水深为300 m为例，计算出横纵荡的数值应在20 m以内，具体参数如表4所示。

表4 百年一遇平台六自由度响应设计指标和预测结果对比

对比设计指标可以发现，平台的横荡自由度表现良好，其百年一遇预测值为6.40 m，为水深的2.1%，小于平台的极端海况设计指标。纵荡自由度的百年一遇预测值为9.85 m，为水深的3.28%，同样小于平台的极端海况设计指标。垂荡在10年一遇重现期下已达到1.55 m，超过了其百年一遇设计指标1.5 m。在100年一遇重现期下的预测值为1.59 m，超过了设计值7%，将可能对海洋平台装备的垂荡相关作业造成影响。横摇与纵摇自由度百年一遇极值分别为2.84°和2.83°，略小于平台的极端海况设计指标3.0°。

3 结 语

半潜式平台在深海中遭受的海洋环境荷载复杂，平台运动响应一旦超出设计指标，将导致平台的结构失效，带来经济损失。基于在“南海挑战号”FPS的一年监测数据开展六自由度响应分析和极值预测研究，结论如下：

1) 通过分析半潜式平台的六自由度响应，引入广义极值分布模型，对一年的响应数据开展分布规律分析，经K-S检验，除艏摇符合Gumbel分布外，其余响应均符合Weibull分布。

2) 对重现期1年、10年、25年、50年、100年的响应极值进行预测，并与设计指标进行对比，发现平台的横荡、纵荡等五个自由度表现良好；而垂荡在10年一遇的极值预测时，已经超过了设计指标1.5 m，高于平台初始设计指标，如现场作业与垂荡有关时，应予以注意。

3) 利用“南海挑战号”FPS实测响应数据，分析响应的分布规律并预测多年一遇极值，对于平台的安全作业、预警十分重要，可将预测结果作为极端恶劣海况下，人员提前撤离的辅助决策支持。通过更新平台的监测数据进行极值分析和预测研究可评估平台的性能变化行为。

4) 由于实测数据量为一年周期，对于较长重现期的响应预测，可能出现极值分布模型的参数误差。随着监测周期的增加，监测数据的逐渐丰富，文中所发展的响应分析和极值预测方法可以得到更为准确的长期极值预测结果。