基于模糊Petri网络的FPSO单点多管缆干涉风险评估

余建星，曾庆泽，余 杨，陈海成，吴世博，范海昭

(1. 天津大学 水利工程仿真与安全国家重点实验室，天津 300072; 2. 天津大学 天津市港口与海洋工程重点实验室，天津 300350)

在波、流和浮体运动等作用下，海洋管线的水下形态会发生变化，使管线受到不同程度的拉伸、扭转、弯曲和挤压，并与周围管线相碰撞，引发干涉现象。干涉现象的发生容易使管线相互缠绕，周期性的碰撞也会造成管线的磨损、疲劳与断裂，危及工程安全。FPSO内转塔式单点系泊系统水下管缆众多，如系泊缆、立管、电缆等，在作业过程中，错综复杂的管汇受多种因素影响容易产生干涉风险，影响FPSO系泊能力，并对人员生命安全和设备财产安全造成危害。因此，对FPSO进行管缆干涉问题的安全性研究具有重要意义。

在管缆干涉问题的研究上，DNV-RP-F203规范[1]对相邻立管的间距作出了规定以保证不发生碰撞；API RP 2RD[2]指出，上游立管产生的尾流会使作用在下游立管的流速减小，导致相邻立管的间距变小并引发碰撞；裴晓梅等[3]研究了拖曳力系数、单位长度质量、外径等参数对非黏接柔性立管干涉的影响；He等[4]提出了一种基于碰撞允许原理的立管干涉概率评估方法；Bai等[5]研究了脐带缆与立管间的干涉，发现水深、浪向和管长对干涉具有不同影响；何杨等[6]根据DNV规范介绍了深水立管干涉的分析方法，总结了影响立管干涉的因素；康庄等[7]通过建立干涉分析非线性时域模型，研究了浪流方向对立管干涉的影响。上述学者对管缆干涉的研究多集中在数值模拟和力学分析上，还鲜有对管缆干涉风险进行定量评估与分析，而针对FPSO单点系泊系统多管缆干涉的风险评估更是空白，不仅缺乏对风险源的全面辨识，还缺乏系统的管缆干涉风险评估体系。

鉴于FPSO单点多管缆干涉风险评估研究方面的不足，提出了一种基于模糊Petri网络(Fuzzy Petri Net, 简称FPN)的定量风险评估方法，利用Petri网络的并行计算能力来处理各级风险因素之间的关系，以此建立了一套系统的FPSO单点多管缆干涉风险评估流程。首先通过识别FPSO单点多管缆干涉的风险因素建立了一个多层次的风险评估指标体系，并根据模糊Petri网理论转换为FPN模型。考虑到传统模糊语言评价方法存在的不足，采用三种形式的模糊置信结构来表示专家的主观评价以提高准确性。将变权理论引入到模糊推理算法中，综合采用层次分析法和变权理论确定风险指标的权重值，令权重根据实际工程情况进行动态变化，最后通过模糊推理算法迭代求解库所可信度和状态矩阵，并计算各级指标的综合评估值。通过上述风险评估流程对南海某内转塔式FPSO的单点多管缆干涉风险进行了实例评估，得出了该FPSO的风险评估等级，由风险排序找出其中的薄弱环节并提出相应的控制与预防措施，以降低风险发生概率并提高安全性。

1 风险评估指标体系建立

辨识风险因素是风险评估的首要环节。因目前有关管缆干涉风险评估的研究较少，且缺乏相关事故案例可供参考，使风险辨识的难度加大。这里从管缆干涉的致灾机理出发，通过调研单点系泊系统的失效模式[8]与管缆干涉研究[3-7]的相关文献，并咨询领域专家的意见，在遵循同一层次的各风险指标相互独立的原则上，建立了如图1所示的多层次风险评估指标体系。其中，最上层(目标层)是一级指标；中间层(准则层)是5个二级指标；最低层(指标层)是30个三级指标。指标的具体描述见表1。

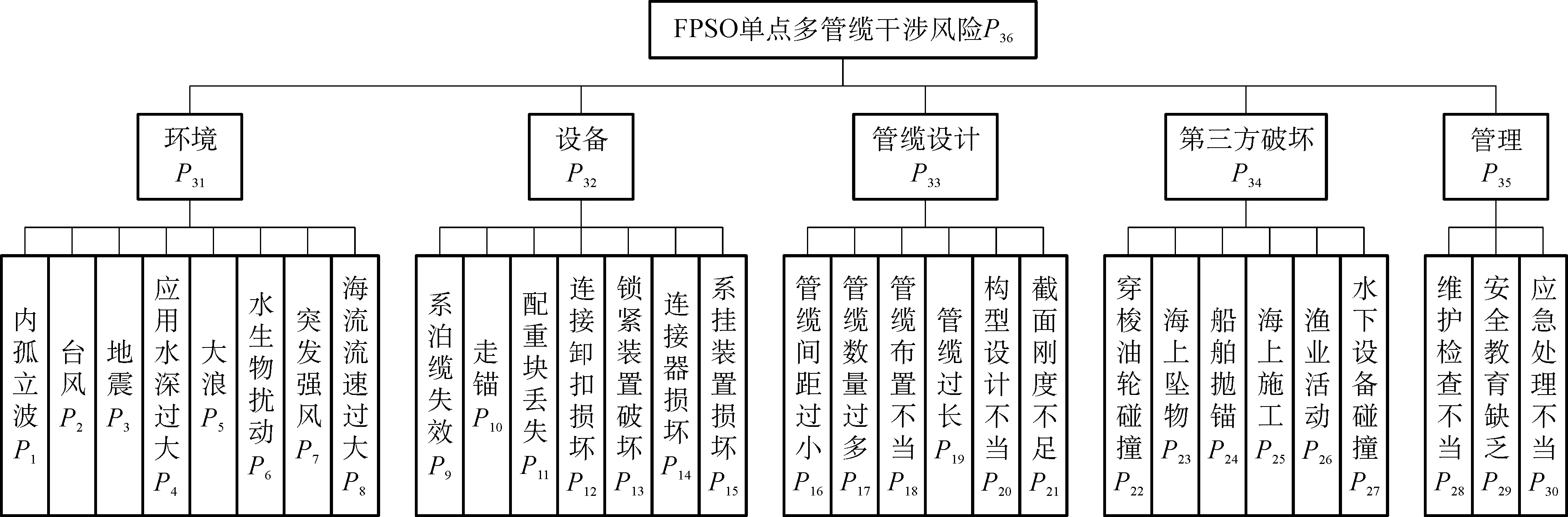
图1 风险评估指标体系Fig. 1 Risk evaluation index system

2 模糊Petri网络模型

2.1 模糊Petri网络理论

2.2 模糊Petri网络模型建立

模糊产生式规则用于表示风险因素的逻辑关系，分“与”规则和“或”规则两种[10]。采用“或”规则进行表示：当任意三级指标风险发生，认为系统存在风险并将引起上一级风险发生。“或”规则表示如下：

Ifd1(w1) ord2(w2) or……ordn(wn)，thendc(wc) (CF=μ1,μ2,……,μn)，wc=max(w1μ1,w2μ2,……,wnμn)

式中：d1,d2,……,dn为前提，dc为结论，w1,w2,……,wn为前提可信度，wc为结论可信度，μ∈[0，1]为规则置信度。

采用“或”规则将指标体系转换为FPN模型，以圆形表示库所、矩形表示变迁，二者通过有向弧进行连接，如图2所示。其中，库所P1～P30表示三级指标，P31～P35表示二级指标，P36表示目标层。

图2 风险评估指标体系的FPN模型Fig. 2 FPN model of risk evaluation index system

3 数据获取方法

3.1 赋权方法

赋权方法分为主观、客观和组合赋权三种。主观赋权法通过专家判断计算指标权重，适用于难以定量描述的指标，但权重受人为影响较大；客观赋权法根据指标信息进行计算，结果更客观，但具有一定机械性，过于依赖样本数据。组合赋权法[10]综合采用主观和客观赋权，能够结合两者优点并弥补不足。

因目前关于管缆干涉风险评估的研究较少，缺乏足够的数据信息，且有些风险指标为定性指标，故难以通过客观赋权法计算风险因素权重。基于该考虑，采用层次分析法和变权理论来综合确定风险因素权重，通过专家经验进行判断，避免了数据不足的影响，并能根据实际工程情况进行变权，使权重分配更加合理。邀请了10位海油工程的专家，相较于其他研究中邀请3～5位专家的做法，能够减小个别专家意见存在较大出入而带来的影响。令10位专家组成专家组，获得各级风险指标下的判断矩阵，由层次分析法计算风险因素的常权重。层次分析法具体步骤在此不做赘述，专家信息见表2。

表2 专家信息

变权理论是相对于常权重而言的，分为惩罚型变权和激励型变权两类。在进行实际工程的风险评估时，对于某些评估值较高的指标，会对系统产生重大影响，需要进行重点关注。若采用常权重进行风险评估，将无法体现该指标的影响，导致评估结果与实际不符，降低评估的准确性。因此，采用变权理论对风险指标进行动态变权，令权重值随指标评估值的大小而变化，可使权重分配更科学合理，更符合实际情况。

采用激励型状态变权向量[11]来对常权重进行动态变权：

(1)

(2)

式中：S(x)=[S(x1)S(x2) ……S(xn)]为激励型状态变权向量，满足S(x)为单调递增的连续函数；a∈[0,1]，表示激励水平，在文中根据库所可信度的平均水平将a设为0.5；C(x)=[C1(x1)C2(x2) ……Cn(xn)]为常权重向量；V(x)=[V1(x1)V2(x2) ……Vn(xn)]为变权后的权重向量。

3.2 模糊理论

3.2.1 模糊置信结构

将库所可信度和变迁置信度分为五个模糊评估等级：H={H11,H22,H33,H44,H55}，表示“极低”“低”“中等”“高”和“极高”，在论域[0,1]内进行划分，模糊语言集见表3。但考虑到传统模糊语言评价无法跨越多个等级进行评估，如当专家认为指标的评估等级处于“低”到“中等”之间时，传统模糊语言评价无法进行表示。故提出三种形式的模糊置信结构[12]来表示专家主观评价以提高评估准确性:

表3 模糊语言集

1) 独立式：置信结构形式为{(Hii,1.0),i=1,2,3,4,5}，表示指标模糊评估等级为Hii，隶属度为1.0。

2) 区间式：置信结构形式为{(Hij,1.0),i=1,2,3,4,j=i+1,……,5}，表示指标模糊评估等级在Hii到Hjj之间，其对应的梯形模糊数为Hii与Hjj所对应的梯形模糊数的综合。

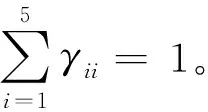
3.2.2 加权综合与去模糊化

对于指标Pn，令专家Zm(m=1,2,……,M)以三种形式的模糊置信结构进行评价，得到专家Zm的评价为：

(3)

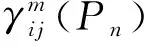
结合专家权重βm(m=1,2,……,M)将M位专家的评价结果进行加权综合，形成一个综合置信结构：

Gn={Hij,γij(Pn),i、j=1,2,3,4,5,i≤j}

(4)

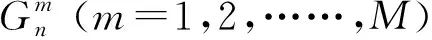
(5)

之后将综合置信结构转换成梯形模糊数R=(R1,R2,R3,R4)，其标度值Rk(k=1,2,3,4)可由下式取得：

(6)

式中：rk(Hij)(k=1,2,3,4)为等级Hij对应的梯形模糊数的四个标度值。

最后由重心法将R去模糊化，可得到指标Pn的评估值：

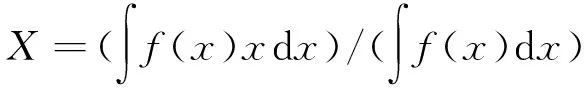
(7)

4 模糊推理算法

利用模糊Petri网络的并行计算能力和矩阵运算能力，提出了库所可信度和状态矩阵推理算法，来迭代求解库所可信度与风险等级评估值，完成综合风险评估。

4.1 库所可信度推理算法

库所可信度推理算法[13]基于模糊产生式“或”规则计算原理，具体推理步骤如下：

第一步，定义两个推理算子：

2) ⊕：A⊕B=C，其中，cij=max(aij,bij)，i=1,2,……,n，j=1,2,……,m。

第二步，令迭代次数k=0，并确定初始库所可信度矩阵α(0)、变迁置信度矩阵U和权值矩阵W：

其中，α(0)为n×1维矩阵，U为n×m维矩阵，初始库所可信度和变迁置信度令10位专家以三种形式的模糊置信结构对指标进行评价后由式(3)～(7)计算获得，专家权重均为0.1；W为n×m维矩阵，其元素Wij表示库所Pi对于变迁tj的权值，因采用模糊产生式“或”规则，若Pi是tj的输入库所，Wij为1，否则为0。

第三步，计算等效模糊真值向量：

E(k+1)=WT×α(k)

(8)

第四步，计算新的库所可信度矩阵：

α(k+1)=α(k)⊕[U·E(k+1)]

(9)

若α(k+1)=α(k)，则迭代结束，输出最终库所可信度矩阵；否则令k=k+1，重复第三步。

4.2 状态矩阵推理算法

在状态矩阵推理算法[14]中引入变权理论，具体步骤如下：

第一步，定义两个推理算子：

1) ⊗：D⊗B=C，其中B、C为n×m维矩阵，D为1×n维矩阵，cij=di×bij；

2) ⊕：A⊕B=C，其中A、B、C为n×m维矩阵，cij=max(aij,bij)，i=1,2,……,n，j=1,2,……,m。

第二步，令k=0，并确定初始状态矩阵、输入矩阵、输出矩阵、常权重向量与风险等级向量。

按照海洋石油工程风险的严重程度将FPSO单点多管缆干涉风险等级分为5个等级，令专家评估各风险因素发生的后果大小。定义风险等级向量Q=(0.2 0.4 0.6 0.8 1.0)，(0 0.2]对应“极低”，(0.2 0.4]对应“低”，(0.4 0.6]对应“中等”，(0.6 0.8]对应“高”，(0.8 1.0)对应“极高”。具体划分标准如表4所示。

表4 风险等级划分标准

令专家评估库所P1～P30的风险等级，结合专家权重得到风险等级评估向量[15]，数据处理规则如下：若10位专家在评估库所Pi的风险等级时，有5位专家评估为“中等”，4位专家评估为“高”，1位专家评估为“极高”，则风险等级评估向量为(0 0 0.5 0.4 0.1)。综合所有风险等级评估向量可得初始状态矩阵。

第三步，根据库所可信度对三级指标进行变权，激励水平a根据库所可信度的平均水平进行设定：

(10)

(11)

第四步，迭代计算变迁激发后的下一状态矩阵：

M(k+1)=M(k)⊕(V⊗O)[ITM(k)]

(12)

第五步，若M(k+1)=M(k)，则迭代结束；否则令k=k+1,回到第四步重复计算，直至相等。

第六步，计算库所的风险等级评估值：

D=M(k)QT

(13)

第七步，结合库所可信度计算综合评估值：

fi=wi×Di

(14)

5 实例分析

现以南海某内转塔式FPSO单点系泊系统为例进行风险评估，对提出的方法进行验证说明。

5.1 库所可信度推理

首先，确定初始数据。初始库所可信度矩阵α(0)与变迁置信度矩阵U表示如下：

α(0)=[0.685,0.438,0.291,0.498,0.826,0.545,0.851,0.799,0.633,0.485,0.623,0.473,0.54,0.568,0.425,0.49,0.428,0.285,0.388,0.30,0.32,0.223,0.45,0.35,0.216,0.340,0.293,0.405,0.413,0.283,0,0,0,0,0,0]T

U={μij}36×35，i=1,2,……,36，j=1,2,……,35。其中，μ31,1=0.769，μ31,2=0.922，μ31,3=0.922，μ31,4=0.783，μ31,5=0.784，μ31,6=0.568，μ31,7=0.730，μ31,8=0.866，μ32,9=0.905，μ32,10=0.735，μ32,11=0.816，μ32,12=0.878，μ32,13=0.888，μ32,14=0.905，μ32,15=0.896，μ33,16=0.888，μ33,17=0.879，μ33,18=0.796，μ33,19=0.762，μ33,20=0.797，μ33,21=0.808，μ34,22=0.922，μ34,23=0.553，μ34,24=0.665，μ34,25=0.922，μ34,26=0.498，μ34,27=0.853，μ35,28=0.905，μ35,29=0.779，μ35,30=0.863，μ36,31=0.888，μ36,32=0.850，μ36,33=0.888，μ36,34=0.801，μ36,35=0.777；其余元素为0。

α(0)表示P1～P30的库所可信度，P31～P36的库所可信度通过后续迭代得到；U表示t1～t35的变迁置信度。通过迭代计算，得α(2)=α(3)，迭代结束，则最终库所可信度矩阵如下：

α(2)=[0.685,0.438,0.291,0.498,0.826,0.545,0.851,0.799,0.633,0.485,0.623,0.473,0.54,0.568,0.425,0.49,0.428,0.285,0.388,0.30,0.32,0.223,0.45,0.35,0.216,0.34,0.293,0.405,0.413,0.283,0.692,0.573,0.435,0.250,0.367,0.614]T

可知，环境、设备、管缆设计、第三方破坏和管理五个因素存在风险的可信度分别为0.692、0.573、0.435、0.250、0.367，而目标层FPSO单点多管缆干涉风险的可信度为0.614，说明环境与设备因素发生风险的可能性较高，并将引起管缆干涉风险的发生。

5.2 状态矩阵推理

首先，确定初始数据。常权重向量C与初始状态矩阵M(0)表示如下：

C=[c1c2c3c4c5c6]

c1=[0.167 0,0.279 8,0.061 5,0.036 4,0.103 9,0.044 6,0.103 9,0.202 8]；

c2=[0.171 2,0.066 6,0.074 5,0.131 4,0.243 1,0.169 9,0.143 4]；

c3=[0.332 4,0.210 0,0.108 4,0.076 6,0.182 5,0.090 1]；

c4=[0.338 6,0.083 5,0.122 1,0.178 6,0.051 9,0.225 4]；

c5=[0.163 4,0.297 0,0.539 6]；

c6=[0.309 7,0.265 9,0.221 4,0.070 1,0.132 9]。

其中，c1、c2、c3、c4、c5、c6分别表示五个二级指标和一级指标下的指标常权重。

设激励水平a为0.5，经模糊推理算法迭代，得M(2)=M(3)，迭代结束，最终状态矩阵如下：

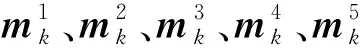
可知，FPSO单点多管缆干涉风险的评估向量为(0.005 0.052 0.244 0.420 0.280)，由式(13)得管缆干涉风险的风险等级评估值为0.784，结合库所可信度得综合评估值为0.481，对应的风险评估等级为“中等”。因此需要对其中的风险薄弱环节提出相应措施来进行预防与控制，进一步降低管缆干涉风险。

5.3 风险控制措施

由模糊推理算法可得各级指标的综合评估值。图3所示为五个二级指标的综合评估值，可知FPSO单点多管缆干涉风险受到多种因素的综合作用，其中环境和设备因素的综合评估值较高，分别为0.547和0.451，说明这二者是影响管缆干涉的主要风险因素，需要对其重点关注。

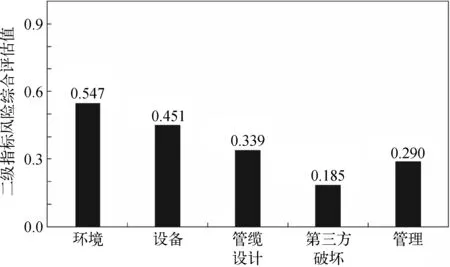
图3 二级指标综合评估值Fig. 3 Comprehensive evaluation value of secondary index

图4为30个三级指标的综合评估值，据此对三级指标进行风险排序，于表5列出了综合评估值大于0.4的10个指标，对其提出风险控制措施如下：

图4 三级指标综合评估值Fig. 4 Comprehensive evaluation value of third-level index

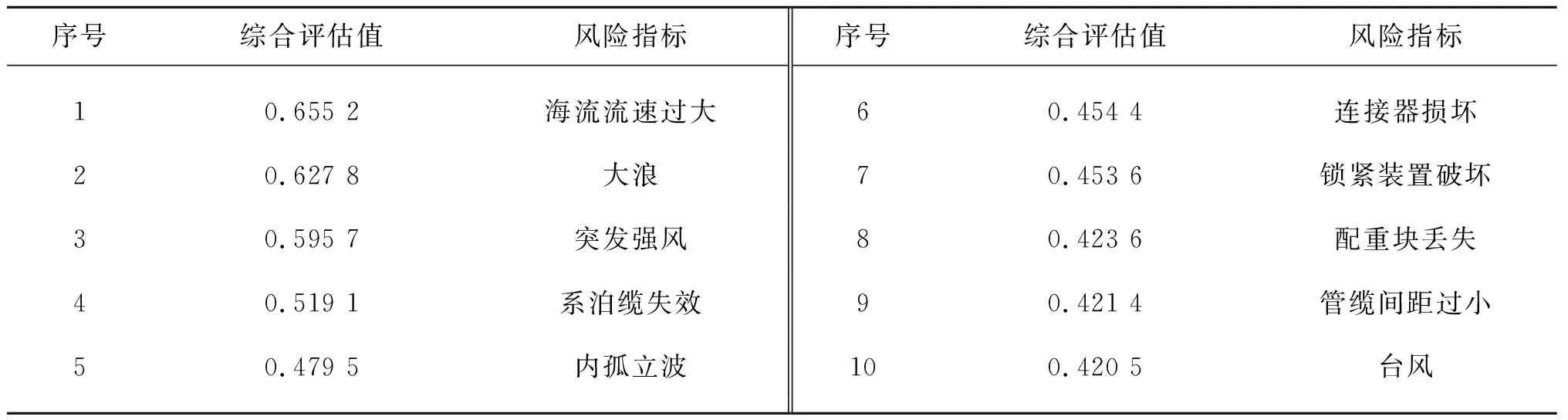
表5 风险指标排序结果

1) 环境方面的主要风险因素包括海流流速过大、大浪、突发强风、内孤立波、台风，该结果符合南海海域实际状况。对此，可增设海上气象预报站，观测周边海域及时对气象情况进行监测、预警，并采取相应处置措施；若出现台风等极端恶劣天气，可考虑解脱单点系泊系统，驶离海域来规避风险。

2) 管缆设计方面的主要风险因素是管缆间距过小。在设计时，应综合考虑规范要求、设计条件与当地海况，设计合适的管缆间距以避免间距过小，并在关键区域安装间隔框以保持足够间距。

3) 设备方面的主要风险因素包括系泊缆失效、连接器损坏、锁紧装置破坏、配重块丢失。对此，应对这些设备进行定期检查与维护，并及时更换失效与损坏的设备。此外，系泊缆失效主要由腐蚀、疲劳和磨损引起，应设定合适的腐蚀余量，提高系泊缆的抗腐蚀性能，做好防腐措施；减少系泊缆的初始缺陷，避免出现局部应力集中，延长疲劳寿命；定期清理链环中的异物，张紧锚链并重点关注锚链触地段易磨损区域，以防止磨损。对于配重块丢失问题，可直接焊接配重块或采用配重链替代配重块。

5.4 对比分析

鉴于文献[10]和[14]采用组合赋权法来确定风险因素的权重，将变权理论的赋权方法应用于文献[10]和[14]的案例中，分别与层次分析法和组合赋权法得到的结果进行对比，根据案例中的库所可信度平均水平，在变权向量中取激励水平a为0.8。因权重值不会影响三级指标的排序，仅对目标的综合评估值产生影响，采用各方法得到的目标综合评估值如表6所示。由表可知，通过变权理论得到的目标综合评估值相较于层次分析法更接近于组合赋权法得到的结果，说明在缺乏数据难以采用客观赋权法的情况下，通过指标的实际情况进行动态变权能够在一定程度上使结果更加客观准确，也证明了本文所提出方法的准确性。

表6 对比结果

6 结 语

针对FPSO单点系泊系统的多管缆干涉风险，提出了一种基于模糊Petri网络的风险评估方法。综合考虑环境因素、设备因素、管缆设计因素、第三方破坏因素和管理因素5个方面来识别FPSO单点多管缆干涉的风险因素，建立了具有30个三级指标和5个二级指标的多层次风险评估指标体系，并转换为FPN模型，通过模糊推理算法对南海某内转塔式FPSO进行了单点多管缆干涉风险评估，得到的主要结论如下：

1) 采用三种形式的模糊置信结构表示专家的评估语言，克服了传统模糊语言评价的不足，使专家的模糊语言表示更加灵活准确，能够减小专家主观判断所产生的偏差。

2) 考虑到海洋环境与实际工程的复杂与多变，综合采用层次分析法和变权理论来确定风险因素的权重，在实例风险评估时可根据风险因素的库所可信度来对常权重进行动态变权，提高危险指标的权重值，在后续的模糊推理中突出其负面影响，使指标赋权更符合实际工程情况，克服固定权重的局限性，并通过对比分析，证明了该方法的可行性与准确性。

3) 通过实例分析，由模糊推理算法得到该FPSO的单点多管缆干涉风险综合评估值为0.481，对应风险评估等级为“中等”，存在一定风险，需要采取适当措施。在二级指标中，环境与设备因素是影响管缆干涉的主要因素，其综合评估值分别为0.547和0.451，该结果符合FPSO的实际情况，验证了方法的可行性。在三级指标中，通过风险排序得到综合评估值大于0.4的指标共有10个，对其提出了相应的风险控制措施，以降低管缆干涉风险的发生概率与严重程度。