LNG工作船组铰接状态下的运动分析
2018-03-01,,,,,
,,,,,
(1.中远海运重工有限公司,辽宁 大连 116600;2.大连理工大学 船舶工程学院,辽宁 大连 116024)
我国及东南亚沿海有相当多的小型边际气田,因其具有储量较小、远离管网等不利因素未能得到有效开发。为了满足小型气田和边际油田伴生气开采、处理及运输的需求,开发具有天然气液化、储运和再气化功能的工作船组,应用共享模块的设计理念,通过铰接方式实现各作业船舶之间的分离与连接。
多浮体铰接状态下的运动性能分析结果决定了该设计方案的安全性和可靠性,是亟需解决的关键技术。
在销钉铰接状态下,各船体之间只有相对纵摇而没有相对横摇与艏摇。关于波浪中多浮体的铰接运动分析,通过把销钉铰接浮体之间的相对转动定义为广义运动模态的方式,Newman在WAMIT中实现了多个铰接浮体的运动和铰接点处的剪力的计算分析[1]。勾莹等[2]应用边界积分方程方法研究了波浪与2个相连浮箱之间的相互作用,并且考虑了浮箱之间的水动力干扰。沈庆则采用多刚体力学分析方法,把铰接多浮体系统看作为铰接无根树系统,分析了多浮体系统在波浪中的运动响应[3]。基于线性势流理论,王桂波等[4]利用频域模态法研究了铰接多浮体在规则波下的运动特点。张亚群等[5]对鹰式波浪能装置多个浮体的力学特别进行了分析,研究了多浮体的运动及阻尼力,铰接力等参数。韦斯俊等[6]应用势流理论计算了多浮体波浪能发电装置的频率水动力,分析极浅水状态下,多浮体系统的锚泊运动特性。
相比于AQWA[7],其他一些商业水动计算软件都没有提供连接多浮体的铰接约束单元,例如,Hydrostar,Wadam等。为了扩展一般商业水动力软件的应用范围,以便其能够进行多浮体铰接水动力计算分析,提出应用刚度矩阵来代替铰接约束单元的方法,并且基于Hydrostar来开展相关研究[8]。
在运动分析时,相对于铰接点,建立两船体之间的6个自由度刚度矩阵。假定两船体相对纵摇自由度上的刚度为零,其余5个自由度上的刚度为无穷大,以此刚度矩阵来模拟销钉铰接约束。利用力的平移定理将相对于铰接点的刚度矩阵转化为相对于船体重心的刚度矩阵,分析研究销钉铰接状态下各船体的垂荡、横摇和纵摇运动RAO,并且与AQWA的计算结果进行对比,来论证采用刚度矩阵的方法在Hydrostar中开展多浮体铰接运动分析的可行性。同时,两套不同方法计算结果的相互映证,也可以更加有力地说明多浮体铰接运动分析结果的合理性。最后,分析结果揭示了铰接多浮体在波浪中的运动特点,为工程应用提供了重要的理论依据。
1 计算模型与理论简介
1.1 计算模型
某作业工况下的LNG工作船组概念包括1艘FLNG和2艘与FLNG铰接的LNG运输驳船,如图1所示。

图1 天然工作船组铰接示意
FLNG与LNG驳船的主尺度见表1。

表1 天然气工作船组主尺度
1.2 理论简介
在铰接状态下,多浮体的运动方程与两浮体的并没有本质上的区别。本文以A、B两铰接浮体在波浪中的运动为例进行理论说明,运动方程如下[9]。
[-ω2(MA+aAA)-iωbAA+CA)]ξA+
(-ω2aAB-iωbAB)ξB=fwA+FK
(1)
[-ω2(MB+aBB)-iωbBB+CB]ξB+
(-ω2aBA-iωbBA)ξA=fwB-FK
(2)
式中:MA、MB分别是浮体A和B的质量阵;aAA、aBB是浮体加速度引起的作用于自身的附加质量;bAA、bBB是浮体速度产生的作用于浮体自身的阻尼系数;CA、CB分别是A、B浮体的静水刚度矩阵;aAB、bAB是B浮体运动引起的作用于A浮体的附加质量与阻尼系数。同理,aBA、bBA则表示A浮体运动引起的对B浮体的附加质量与阻尼系数;fwA、fwB是A和B浮体受到的波浪激励力;Fk表示A、B两浮体之间的铰接力。在Hydrostar中,Fk用刚度矩阵与相对位移乘积的形式来表示。
假定B浮体固定不动,A浮体发生一阶运动位移,重心处的运动位移表示为
ξA=(x,y,z,α,β,γ)T
(3)
式中:x、y、z分别表示A浮体重心处的3个线位移,α,β和γ表示浮体A的3个角位移。
在A与B浮体的铰接点处,产生的线位移为
H=(x,y,z)T+(α,β,γ)×r
(4)
式中:r为由A浮体重心指向铰接点的位置矢量。
由于A与B浮体在铰接点处销钉约束,两浮体只有相对纵摇,故相对于铰接点的刚度矩阵K可以表示为
(5)
式中:k1至k6为无穷大,k5为零。
铰接力FK中相对于铰接点的3个线力FKL可以表示为
(6)
而铰接力Fk中相对于铰接点的3个力矩FKM则表示为
(7)
应用力的平移定理,将相对于铰接点处的铰接力平移到浮体A的重心处。
相对于浮体A重心的3个铰接线力由FGL表示,相对于重心的铰接力矩由FGM表示。
FGL=FKL
(8)
(9)
由式(8)和式(9)即可得到相对于浮体重心的刚度矩阵。
2 结果与分析
如图1所示,FLNG左右两端各由销钉铰接一艘LNG驳船,构成三浮体铰接系统。相对于销钉铰接点的刚度阵取值如式(10)所示。
可以通过FLNG承受的一阶波浪激励力来初步选择上述刚度阵的刚度值。FLNG垂荡波浪激励力比纵摇激励力矩小一个数量级;横荡激励力比横摇激励力矩小一个数量级。故角位移刚度比线位移刚度大一个数量级。垂荡波浪激励力的量级是107N,两船之间的相对位移(除了纵摇外)至少比一阶位移小两个量级左右,所以选取线位移刚度为1010N/m,角位移刚度为1011Nm/rad。此外,为了更加合理地确定刚度值,建议对刚度阵进行敏感性分析,同时再结合计算结果和后处理动画判断刚度的设置是否合理。
2.1 横摇运动
45°、60°和90°浪向下,销钉铰接三浮体横摇运动RAO曲线如图2所示。根据销钉铰接约束的特点,3个浮体的横摇运动应该是一致的。由图可得,在3种不同浪向角下,3个浮体的横摇运动曲线都是完全重合的,计算结果符合销钉铰接约束的特点。这一运动特点从一个方面证实了在Hydrostar上可以利用刚度矩阵的方法对铰接约束多浮体运动进行模拟分析。
图3分别展示了在45°、60°和90°浪向下应用不同水动力分析软件计算得到的FLNG横摇运动的RAO。在45°浪向下,AQWA与Hydrostar的计算结果,除了低频处有少许差别外,其他频率处两者吻合得很好。而且还应该注意到,45°浪向下,横摇运动RAO的数值本身就很小,在低频附近出现计算结果不一致的原因,很可能是数值误差导致的。在60°和90°浪向下,AQWA与Hydrostar的计算结果在整个计算频率范围内都吻合得很好。由此可得,刚度矩阵法可以在Hydrostar中实现铰接浮式系统的横摇运动分析。
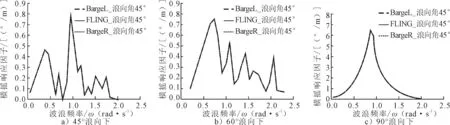
图2 横摇RAO

图3 浪向下FLNG横摇运动对比
90°浪向下,铰接三浮体的横摇共振频率约为0.9 rad/s,其最大横摇RAO稍大于7(°)/s。而浪向变为60°后,横摇RAO的数值迅速减小,其最大值约为0.8(°)/s。可见,三船铰接构成细长浮式系统的横摇运动,仅在横浪条件下运动幅值比较明显,而在斜浪状态下,横摇幅值迅速减小。
2.2 垂荡运动
0°、45°和90°浪向下,BargeL垂荡运动的AQWA与Hydrostar计算结果如图4所示。AQWA与Hydrostar的计算结果基本一致。当频率趋近于2 rad/s时,两者的计算结果都趋近于0;当频率趋近于0时,垂荡运动RAO趋近于1。在90°浪向时,BargeL的垂荡固有频率约为0.9 rad/s。BargeL垂荡运动RAO符合典型浮体在波浪上的运动特点。
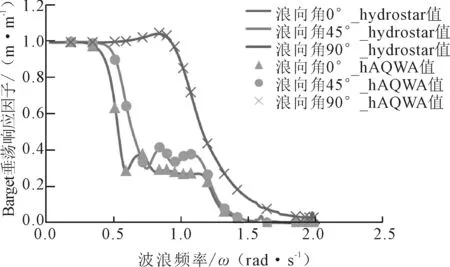
图4 BargeL垂荡运动对比
图5展示了0°、45°和90°浪向时,AQWA与Hydrostar关于FLNG垂荡运动的计算结果。由图5可知,无论是0°、45°还是90°浪向,Hydrostar的计算结果与AQWA的结果都非常吻合。

图5 FLNG垂荡运动对比
BargeR的垂荡运动对比结果如图6所示。与BargeL和FLNG的对比结果一样,AQWA与Hydrostar的计算结果基本一致。由此可得,通过设置适当的刚度矩阵的方法,Hydrostar可以很好地模拟销钉铰接约束。

图6 BargeR垂荡运动对比
0°浪向下,在波浪频率范围为0.8~1.2 rad/s时,BargeL的垂荡运动RAO约为0.3 m/m,明显高于FLNG与BargeR的垂荡运动(小于0.05 m/m)。产生这一现象的原因在于,0°浪向时,BargeL直接受到来波的作用,而FLNG与BargeR受到BargeL的遮蔽。正是因为BargeL的遮蔽效应,导致了FLNG与BargeR在此波浪频率范围内受到较小的波浪激励力,故其垂荡运动明显小于BargeL的运动幅值。
2.3 纵摇运动
图7给出了AQWA与Hydrostar关于BargeL在0°、45°和75°浪向下纵摇运动的计算结果。由图7可知,AQWA与Hydrostar的计算结果吻合得很好。在0°浪向下,BargeL纵摇运动的最大值约为2.6 °/m;45°浪向时,纵摇运动最大值增到2.7 °/m;浪向增加到75°时,纵摇运动幅值的最大值也仅减小了0.6 °/m,约为2.1 °/m,可见铰接三浮体系统的纵摇运动对浪向角的变化并不敏感。不过,不同浪向下纵摇运动最大值对应的频率点的位置发生了较大变化,0°浪向时最大纵摇运动发生在0.5 rad/s附近;45°时最大纵摇值对应的频率变为0.6 rad/s左右;75°浪向时最大纵摇运动则出现在0.9 rad/s附近。
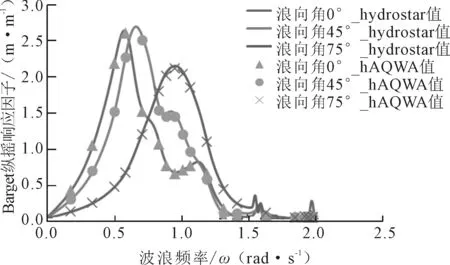
图7 BargeL纵摇运动对比
FLNG在0°、45°和75°浪向下纵摇运动RAO对比结果如图8所示。Hydrostar的结果曲线与AQWA的结果非常一致。
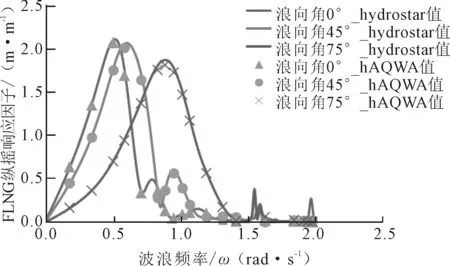
图8 FLNG纵摇运动对比

图9 BargeR纵摇运动对比
图9展示了BargeR在0°、45°和75°浪向下的纵摇运动的计算结果对比。与BargeL和FLNG的对比结果一样,Hydrostar与AQWA的计算结果吻合得也非常好。由以上的对比结果可得,Hydrostar可以很好地模拟铰接三浮体的运动。与铰接三浮体在0°浪向下的垂荡运动类似,当波浪频率在0.7~1.5 rad/s范围内时,BargeL的纵摇运动幅值明显大于FLNG和BargeR的运动结果。而且,在0°浪向下,BargeL的纵摇运动RAO最大值为2.6 °/m,也明显大于FLNG的最大值1.2 °/m和BargeR的最大值2.1 °/m。导致这一现象的原因,同样是由于0°浪向下,BargeL对FLNG和BargR存在遮蔽效应。
3 结论
1)应用刚度矩阵法可以在Hydrostar中开展铰接状态下多浮体运动分析,并且通过与AQWA计算结果的对比,验证了上述方法计算的准确性。对于刚度矩阵的取值,建议进行敏感性分析,并结合一阶波浪激励力的大小选择合适的刚度矩阵。
2)多浮体运动中存在明显的遮蔽效应,即顶浪浮体的垂荡和纵摇运动明显高于被遮蔽的浮体。故在多浮体系统设计时,应重点关注迎浪浮体的垂荡与纵摇运动。
3)三船首尾铰接构成的细长多浮体系统,其横摇运动在90°浪向下比较剧烈。当浪向偏斜时横摇运动迅速减小。所以,在布置多浮体系统时,应避免与目标海域的主浪向成90°角。
[1] NEWMAN J N. Wave effects on deformable bodies[J]. Applied ocean research, 1994,16(1):47- 59.
[2] 勾莹,滕斌,宁德志.波浪与两相连浮体的相互作用[J].中国工程科学,2004,6(7):75- 80.
[3] 沈庆,陈徐均.系泊多浮体系统波浪运动响应的动力学分析[J].解放军理工大学学报,2002,1(4):31- 36.
[4] 王桂波,勾莹,滕斌,等.铰接多浮体系统在规则波作用下的运动响应[J].大连理工大学学报,2014(6):618- 625.
[5] 张亚群,游亚戈,盛松伟,等.鹰式波浪能发电装置水动力学性能分析及优化[J].船舶力学,2017,21(5):533- 540.
[6] 韦斯俊,王义,高明,等.极浅水多体波浪能发电装置锚泊系统设计[J].船舶工程,2017(3):70- 76.
[7] ANSYS. Aqwa Reference Manual[M]. ANSYS, 2013.
[8] BV. Hydrostar for Experts User Manual[M]. Paris: Neuilly- Sur- Seine, 2014.
[9] BERNARD MOLIN. 海洋工程水动力学[M].北京:国防工业出版社,2012.
