基于MPC的半潜式无人艇导航轨迹跟踪控制研究

张丽珍,高浩,吴迪,李卫,陆天辰

(上海海洋大学 工程学院,上海 201306)

0 引 言

智能无人艇在海洋物理环境监控、近海安全等科学领域具有重要研究价值[1]．半潜式无人艇作为无人艇大家族中的一员,由于其独特的航行方式,具有能够有效降低海水表面浪区的冲击和影响、隐蔽性好等优点[2],我国在半潜式无人艇方面的研究较国外起步较晚[3],上海海洋大学研究团队开发了一种新型半潜式无人艇．但是在半潜式无人艇导航过程中,使用PID控制方法对导航规划轨迹进行跟踪时,出现跟踪误差较大的问题,最大跟踪误差可达1 m,影响半潜式无人艇的航行稳定性和续航里程．

导航轨迹跟踪是智能无人艇相关研究的一个重要内容．在智能无人艇的轨迹跟踪方面,国内外学者对此做了很多研究[4]．目前,智能无人艇的轨迹跟踪问题主要控制方法有模糊控制[5-6]、模型预测控制(MPC)[7-8]等方法．但是上述研究都是水面无人艇和水下无人艇的轨迹跟踪问题,对半潜式无人艇的导航轨迹跟踪控制研究较少．半潜式无人艇在实际导航航行过程中,存在环境干扰等因素导致的轨迹跟踪误差较大的问题,目前还没有一个实际可采用的控制方法,相关内容的研究也非常少．因此,本文针对半潜式无人艇在导航轨迹跟踪控制方面的问题,提出了一种基于MPC的轨迹跟踪控制方法．首先建立新型半潜式无人艇的运动模型,并在模型的基础上设计了MPC控制器,最后通过仿真和试验对该控制方法的有效性进行验证．

1 半潜式无人艇数学模型建立

1.1 半潜式无人艇运动方程建立

本文研究的半潜式无人艇主要由左、右两个艇体和浮体组成,如图1(a)所示,半潜式无人艇在航行时,二个艇体位于水面以下,搭载通信设备的小体积浮体位于水面上．半潜式无人艇的运动为6自由度的运动,考虑到研究的是水面上的平面运动轨迹,在不影响研究问题的基础上,进行适当简化,所做假设如下:

1) 只考虑纵荡、横荡和艏摇这3个方向的运动,忽略垂荡、横摇和纵摇;

2) 半潜式无人艇关于XOZ平面对称;

3) 半潜式无人艇重心、浮心均在Z轴上．

基于上述假设,六自由度半潜式无人艇模型简化成三自由度运动问题,如图1(b)所示．

(b)三自由度模型

由图1(b)所示，外界干扰下的半潜式无人艇3自由度运动方程为[9-13]:

(1)

(2)

式中:τ11、τ12分别为半潜式无人艇左、右艇体艉部螺旋桨产生的推进力;n1、n2分别为左、右两侧螺旋桨转速;ts为推力减额系数;D为螺旋桨直径;Kt为无因次推力系数;Bs为每个艇体的中心线与坐标点Os之间距离;τ1为半潜式无人艇推力;τ3为半潜式无人艇艏摇力矩．

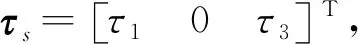
(3)

式中:τdu、τdv分别为波浪在x轴和y轴方向上的干扰力;τdr为波浪干扰力矩;τd可具体表述为

(4)

式中:δs为半潜式无人艇的艏向角;ρ为海水密度;L为浮体长度;B为浮体宽度;si为波频．其中si又可表述为

(5)

式中:Ai为波的幅度;λi为波的长度;wei为频率;φi为时变的相位．

本文建立的3自由度运动模型适用于由水面小浮体和水下双螺旋桨驱动的双艇体组成的半潜式无人艇,且风的干扰可忽略不计,只考虑波浪的干扰．

1.2 半潜式无人艇的状态空间方程

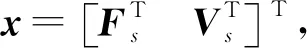
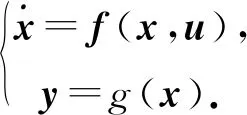
(6)

输出方程为线性方程,

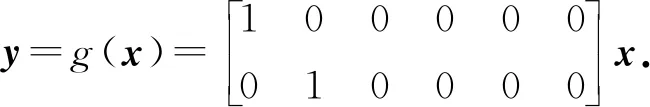
2 MPC控制器设计

在半潜式无人艇进行导航轨迹跟踪的过程中,首先根据半潜式无人艇的初始状态(位置,航向角,速度),结合半潜式无人艇的预测模型得出系统的预测输出;然后将预测输出和参考轨迹的误差值和系统约束参数结合目标函数,求解出控制量;最后将控制量和外界干扰量共同作用到半潜式无人艇并保持一个控制周期,并将半潜式无人艇新的运动状态输入至预测模型中,完成一个周期内的控制过程,基于MPC的半潜式无人艇导航轨迹跟踪控制原理如图2所示．为了使上述过程便于实施,首先对半潜式无人艇的状态空间方程进行线性化和离散化,得到新的离散化状态空间方程;然后结合新的离散化状态空间方程、目标函数和系统约束,可将半潜式无人艇导航轨迹跟踪问题转化为最优值问题进行求解．

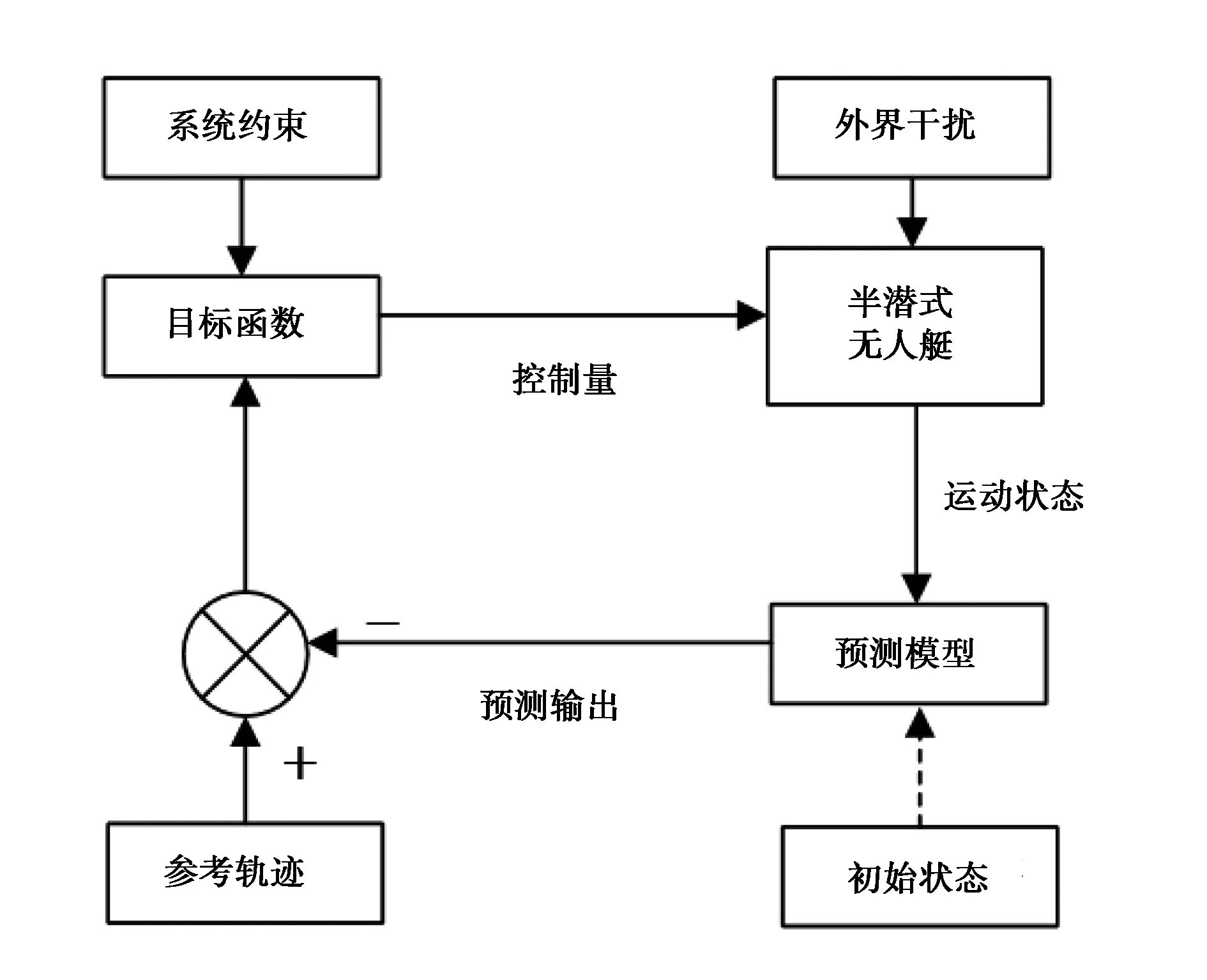
图2 MPC轨迹跟踪控制原理图

2.1 状态方程线性化

式(6)中状态方程为非线性方程,不适宜用作控制器的设计．为了便于控制器的实现,对上述非线性状态空间方程进行线性化后,再离散化．

在模型预测控制中,非线性系统近似为线性系统时,通常采用近似线性化方法[15]．在任意参考点(xa,ua)处线性化后的状态方程:

(7)

2.2 状态空间模型离散化

用欧拉法[16]对式(7)离散化,并联立式(6),可得半潜式无人艇离散化线性状态空间方程为

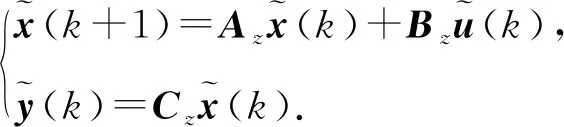
(8)

2.3 MPC预测方程

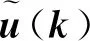
可得到如下新的离散化状态空间方程:

ξ(k+1)=Asξ(k)+BsΔu(k),

y(k)=Csξ(k).

(9)

为了简化运算,假定在系统预测时域Np内,

Az+i=Az,Bz+i=Bz,i=1,2,…,Np.

(10)

由式(9)和(10),可得系统的预测方程为

Ys((k+1)|k)=Wsξ(k)+WuΔU(k),

(11)

式中:Ys((k+1)|k)表示k时刻对k+1时刻的预测输出;ΔU(k)为控制时域Nc内的预测输入量;Ws和Wu为系统矩阵．各项具体定义如下:

2.4 目标函数

以系统输出量的偏差、控制量增量来构建目标函数:

(12)

为避免目标函数无可行性解,加入松弛因子[17],目标函数为

(13)

式中:ΔY((k+i)|k)为输出量和期望量之差;Nq为输出加权矩阵;Nr为控制加权矩阵;ε为松弛因子;ρ为权重系数．该式第一项反映半潜式无人艇跟踪控制器的跟踪能力;第二项反映半潜式无人艇运动的平稳性,保证控制增量较小,同时较小的控制增量可减少控制系统对半潜式无人艇的航向角的调整幅度,可在一定程度内减少系统的能源消耗．由式(8)和式(11),可得到如下标准二次型目标函数:

(14)

其中:

2.5 系统约束

由于半潜式无人艇运动情况受到其机械性能的影响,需要对控制参数进行约束,约束条件可以表示为

Umin≤U(k)≤Umax,

ΔUmin≤PΔU(k)+U(k)≤ΔUmax.

(15)

半潜式无人艇航行速度参数如表1所示．

表1 半潜式无人艇航行速度参数

根据表1中的数据和文献[18],对控制量和控制增量做如下约束:

2.6 最优值问题转化与求解

综合上述的目标函数和系统约束条件,基于MPC的半潜式无人艇航迹跟踪可以描述为最优值问题．由式(11)、(13)及(15),基于MPC的半潜式无人艇航迹跟踪问题最终转化为标准二次型函数最优值问题,如式(16)所示．

ΔUmin≤PΔU(k)+U(k)≤ΔUmax.

(16)

对上述的最优值问题,采用QP求解器,可快速求得最优控制序列,输入至半潜式无人艇控制模型,如此循环迭代,实现对无人艇的最优控制输入．

3 仿真及试验验证

为了验证MPC控制器的有效性,搭建MATLAB仿真平台,观察其跟踪航迹线的误差并分析其跟踪性能．为了能够全面地分析控制器的性能,分别在无外界干扰和存在外界干扰两种情况下,对控制跟踪性能进行仿真．为验证本文设计的控制器有效性,采用MPC控制方法和原有PID方法进行对比仿真和试验验证．

3.1 仿真参数设置

仿真中使用的无人艇的基本参数如表2和表3所示,仿真初始参数如表4所示．

表2 半潜式无人艇技术参数

表3 控制器仿真参数

表4 仿真初始参数

图3 仿真流程图

3.2 仿真结果及分析

3.2.1 无外界干扰下半潜式无人艇轨迹跟踪效果

无外界干扰下,仿真结果,如图4所示．

图4 无干扰轨迹跟踪效果图

由图4可见,在无外界干扰的情况下,原有PID控制方法和本文设计的MPC控制方法的轨迹几乎与参考轨迹重合,跟踪误差都比较小,表明二种方法都能使半潜式无人艇快速跟踪上参考轨迹,能够满足设计要求,具有较好的轨迹跟踪效果．

3.2.2 外界干扰下半潜式无人艇轨迹跟踪效果

在外界干扰下,仿真结果如图5～7所示．

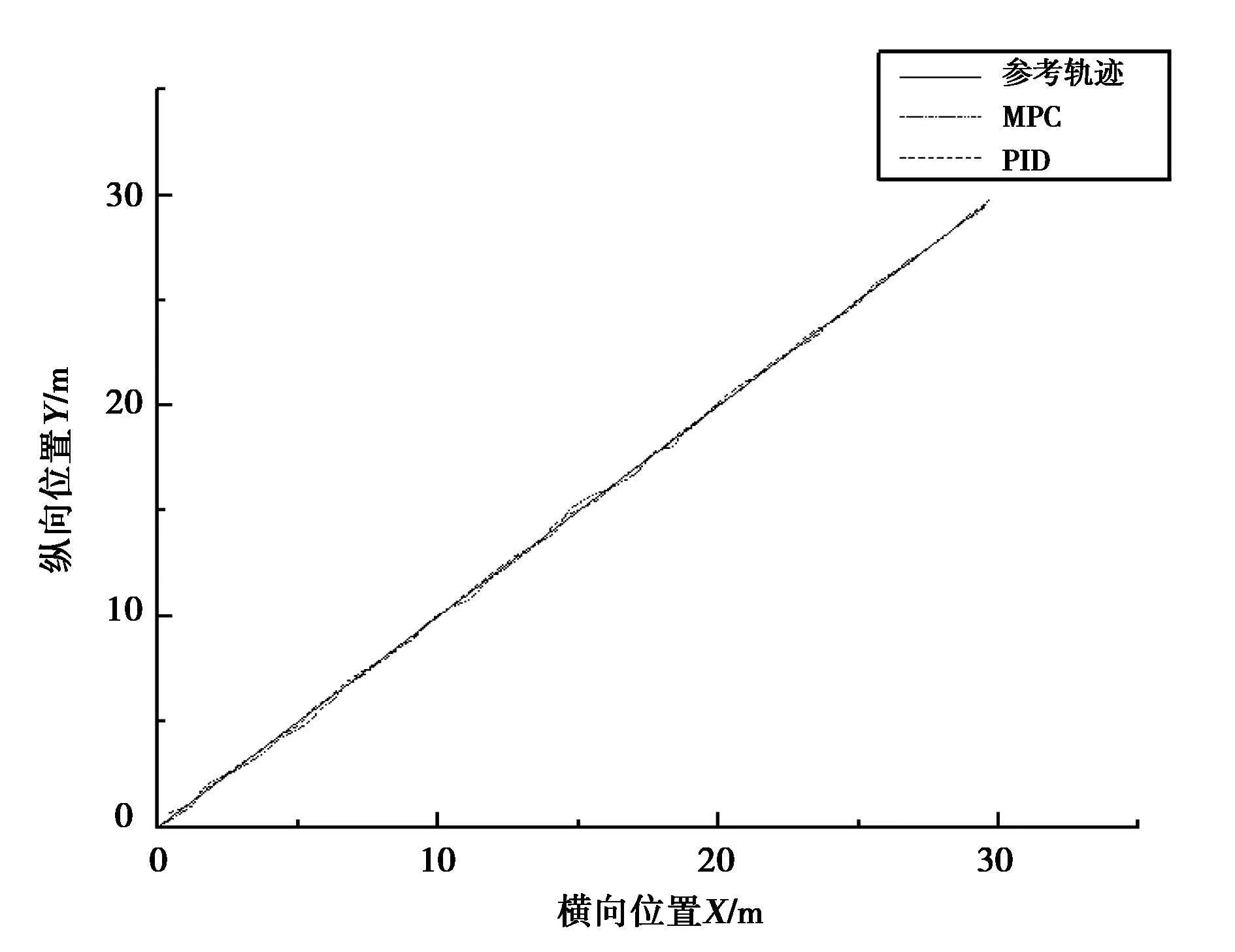
图5 外界干扰下轨迹跟踪效果对比图

图6 跟踪误差对比图

图7 航向角对比图

由图5可知,在有外界干扰的情况下,原有PID控制方法和MPC控制方法都完成了对轨迹的跟踪,MPC控制方法的轨迹跟踪效果比原有PID控制方法更好．综合分析图5～6可看出,原有PID控制方法比MPC控制方法的航迹偏差较大,误差波动也比较大,原有PID控制方法的误差在0.4 ～0.6 m波动,误差最大值可达0.65 m;而MPC控制方法误差波动范围为0.2～0.45 m,误差最大值仅为0.5 m,相比之下,MPC控制方法的轨迹误差更小,轨迹误差可以减小40%～50%．由图7可知,原有PID控制方法的航向角变化幅度比MPC控制方法要大,不仅影响了半潜式无人艇的航行平稳性,同时控制系统还需要耗费更多的能源来调整半潜式无人艇的航向角．综合图5～7,可得:MPC控制方法的轨迹跟踪误差小于原有PID控制方法．

3.3 试验验证及分析

为了进一步验证该控制方法的有效性,对控制方法进行实际环境验证,试验场所选择在上海海洋大学图书馆旁小湖,如图8所示．为了保证仿真与试验的一致性,在试验时,MPC控制器的参数与仿真控制器的参数相同．由于实际环境外界干扰的复杂性,本次试验仅对半潜式无人艇直线导航轨迹跟踪效果进行验证;采用原有PID控制方法和MPC控制方法分别对半潜式无人艇进行直线跟踪试验．试验验证的无人艇采用上海海洋大学研究团队的半潜式无人艇,半潜式无人艇实物如图9所示．试验前,利用半潜式无人艇导航设备设置一条直线参考轨迹,观察并记录半潜式无人艇运行状况,如图10为半潜式无人艇在运行中．

图8 上海海洋大学图书馆旁小湖实拍图

图9 半潜式无人艇实物图

图10 半潜式无人艇试验运行图

在试验过程中,利用半潜式无人艇GPS/BDS定位设备和实时动态(RTK)辅助定位设备读取半潜式无人艇的位置信息,半潜式无人艇的位置误差在20 cm以内．对此次试验采集到的位置信息进行统计后,得到半潜式无人艇的轨迹跟踪误差图,如图11所示．

图11 半潜式无人艇试验轨迹误差图

由图11可知,在实验过程中,MPC控制方法和原有PID控制方法的跟踪误差一直存在,且都在一定范围内波动,但原有PID控制方法的误差值在0.5～1 m波动,MPC控制方法的误差值在0.4 ～0.6 m波动,轨迹跟踪误差减小了50%左右．本文提出的MPC控制方法,相比原有PID控制方法而言,导航轨迹跟踪误差的数值和变动范围更小,较小的跟踪误差,使半潜式无人艇以更短的路径完成对导航参考轨迹的跟踪,可在一定范围内节省能源．

综上所述,本文设计的MPC控制器在满足导航轨迹跟踪效果的同时,可以提高半潜式无人艇航行稳定性,能够减少能源消耗,有效提升半潜式无人艇的续航能力．

4 结 论

为了解决半潜式无人艇在导航航行中轨迹跟踪误差较大的问题,使用了基于MPC的轨迹跟踪控制方法解决这一问题．由仿真和试验结果可得:本文提出的MPC控制方法,相较于原有PID控制方法,能够将导航轨迹跟踪误差减小50%左右,提高轨迹跟踪的精度;同时MPC控制方法能够以更短的路径完成对参考轨迹的跟踪过程,在一定程度上减少能源消耗,有利于实际使用．